基于兴趣点的城市阻抗计算模型

郑松潘, 陈羽中, 於志勇, 郭松荣, 沈　尧

(1.福州大学 数学与计算机科学学院,福建 福州 350108; 2.福州大学 福建省网络计算与智能信息处理重点实验室,福建 福州 350108; 3.伦敦大学学院 巴特雷特建筑学院,伦敦 NW12BX)



基于兴趣点的城市阻抗计算模型

郑松潘1,2, 陈羽中1,2, 於志勇1,2, 郭松荣1,2, 沈尧3

(1.福州大学 数学与计算机科学学院,福建 福州 350108; 2.福州大学 福建省网络计算与智能信息处理重点实验室,福建 福州 350108; 3.伦敦大学学院 巴特雷特建筑学院,伦敦NW12BX)

摘要:为实现城市阻抗的实时计算, 提出一种基于社交网络兴趣点的城市阻抗计算模型.模型以城市路网划分地块为基本单位,综合考虑地块中心到兴趣点间的平均路网距离、转弯角度、转弯次数、交叉口以及人口等因素,计算城市地块在可达半径范围内的阻抗值.将提出的模型与效用模型、潜力模型以每2 h作为时间段进行计算对比.结果表明：提出的阻抗模型与实际路况的相似度比效用模型、潜力模型分别高出80%与60%,有效提高了模型在城市阻抗计算上的适用性,反映出城市地块在不同时间段的阻抗变化.

关键词：城市可达性；阻抗计算；兴趣点(POI)；签到；智慧城市

城市可达性[1]是城市研究中非常重要和基础的概念,表征的是人们在城市中通过交通工具到达目的地的方便程度,即人们从一点到另一点参与活动的便捷程度,已广泛应用于城市规划、交通学、经济学等[2-3]相关研究中.阻抗则定义了起讫点间的出行代价,是描述可达性的重要指标.

对于可达性强度的计算,近年来国内外学者都进行了相应的研究,并提出了相关计算模型.Handy等[4]基于离散选择模型提出效用模型,对区域内的每一个终点设置一个效用值,个体会选择效用最大的点作为出行选择,以此判别可达性的大小.Wachs等[5]提出了累积机会模型,根据某一个范围内可以到达的终点数量来计算可达性强度.累积机会模型简单易理解,但忽略了每个机会点的信息特征、中心和边界的机会点以及不同机会点对人们的吸引力等因素.针对累积机会模型的不足,Hasen等[6]提出基于牛顿重力模型的潜力模型,考虑了中心点与各机会点的关系,通过构建阻抗函数来计算可达性.潜力模型既可用于计算公共兴趣点的可达性,也可用于市场的潜力分析[7],阻抗函数对最终可达性强度的影响比较大.常用阻抗函数包括负指数函数、高斯函数、负幂函数等[8-10],选择何种阻抗函数主要取决于模型的应用范围与所使用数据的特性.以上3种模型在理论上都较易理解和拓展,且模型输入参数简单易获得.但由于选用的参数和计算函数简单易用,往往忽略了复杂的城市道路情况,使得模型准确性不高.

在道路阻抗函数研究中,美国公路局通过回归分析得到了BPR(bureauofpublicroads)速度-流量模型[11].Spiess等[12]针对BPR模型在道路饱和度达到顶峰时结果偏差大的问题,对其阻抗函数作了进一步改进.Davidson等[13]以排队论为理论依据,提出具有渐进性的阻抗函数,在某一范围内对道路行驶时间、距离等和阻抗大小的关系进行参数修正.王元庆等[14]以交通流为改进依据,在阻抗模型中考虑了费用、城市节点、时间等影响因素.以上4种道路阻抗模型加入了道路阻抗的研究,但都需要大量的数据作为支持,包括城市公共设施的地理分布位置信息、不同时间段的道路交通量、研究范围内的人口数据等[15],这些数据在国内难以获取,给城市阻抗模型的研究带来诸多不便.随着互联网以及社交网络的兴起,产生了大量可服务于城市发展决策的移动社交网络数据,通过挖掘分析这些数据,可将其用于城市阻抗模型的构建.

本文以全国路网数据以及新浪位置微博的兴趣点(pointsofinterest,POI)数据为基础,提出一种城市地块可达范围的阻抗计算模型,主要工作如下：

1) 为模型选用合适的数据源.采集、处理城市路网数据,并划分城市地块；采集位置微博POI和POI签到数据,并映射至所属地块.

2) 计算模型参数.规划地块中心点到POI的路径,并利用转换模型计算路径的转弯次数、转弯角度、交叉口等参数.

3) 提出基于POI构建城市地块可达半径下的阻抗计算模型.

1问题描述

为了合理描述阻抗计算问题,量化城市出行代价,首先需要定义模型的讨论范围.引入城市地块的概念,定义如下.

定义1城市地块划分.全国路网数据按照封闭的道路或河流等将城市划分为一个个多边形的地块集合[16-17]{V1,V2,V3,…,Vn},其中Vi=(Gi,Ei),i∈n,G为地块i的边界点集合,E为相邻边界点所构成的边集合,由此构成一个封闭的多边形地块.

以地块作为基本单位进行阻抗模型的讨论,对可达性分析更具有实际意义,因其采用的是实际的城市道路网络和交通距离而非绝对空间距离[18].确定了模型讨论的范围单位后,再确定模型的讨论对象.本文以新浪位置微博的城市POI集合{POI1,POI2,POI3,…,POIk}为参数输入进行讨论,k为POI数量.为了明确地块范围内的哪些POI需要进行讨论,此处引入地块可达半径内POI功能密度概念.

定义2城市可达的功能密度.给定POI集合后,通过经纬度信息可将POI一一映射至所属地块,则城市可达的功能密度为

(1)

式中：ρ表示可达半径下的功能密度,i为第i个地块,r为定义的可达半径大小,j为第j个POI点,k为POI的总数,Fj表示为搜索到的第j个POI是否在其地块的可达半径下.以地块中心点为起点,路网距离为可达半径,搜索每个地块可达半径下的所有POI数量,计算城市可达的功能密度.

城市阻抗计算模型以地块为单位,以地块中心点的可达半径为范围,以范围内的POI为讨论对象,计算每个地块对应的平均阻抗.阻抗值集合为{M1,M2,M3,…Mi…,Mn},n为地块数量,Mi值越大则阻抗越大.

2城市阻抗计算模型

2.1数据预处理

对于有营业时间的POI点(如:商店、餐厅、旅游景点等)阻抗的计算有时间属性,在其营业时间之外,认为其对模型的计算没有意义,因此在构建模型之前需要对时间参数进行过滤.

由于营业时间是用户手动填写,缺乏规范,采集到的数据各式各样、规格不一,部分数据会包含冗余和错误信息,在预处理阶段,需要剔除与时间属性无关的信息,按形如“8:00—20:00”的标准格式提取出正确的营业时间.本文将以2h作为1个时间段,并划分出工作日和周末2类,共24个时间段进行讨论,每个地块的可达功能密度考虑时间参数.

(2)

式(2)表示在选定时间段t内地块i的可达功能密度,β用于判断POI是否在选定的时间段内营业.

2.2路径规划

在获取了每个地块可达半径下对应的POI后,需要一一对其进行路径规划,获得所选择路径的转弯次数、转弯角度、交叉口数等具体参数,用于计算阻抗.本文通过百度地图路线交通API获取地块中心点与POI间的路径规划.

2.3计算模型参数

2.3.1平均路网距离一条路径的路网距离是阻抗模型最重要的计算参数之一.当不同的地块可达POI数量相同时,到达POI所需的路网距离越大,地块的阻抗值就会越大.定义地块平均路网距离参数为

(3)

式中：Di为第i个地块的平均路网距离参数,j为该地块可达半径下的第j个POI点,ρi表示该地块的功能密度,dj为地块中心到第j个POI的路网距离,ε为调节因子.可视化结果如图1所示.

图1　天津市地块平均路网距离Fig.1　Average road network distance of blocks in Tianjin

本文均采用CartoDB[19]大数据地图可视化工具进行结果展示,如图1所示，地块颜色越深则表示计算的值越大.

2.3.2转弯角度从地块中心到达POI的路径中,包含多次的转弯,转弯的角度和方向对阻抗有着较大的影响.其中,转弯的方向在道路交叉口处体现；而转弯的角度越大,自然阻抗也会越大,因此,城市阻抗计算模型须对路径上的转弯角度予以考虑.

在百度地图的路径规划中,一条实际的直线路段,通过GPS定位后可能包含许多微小的转弯折角,路径规划API返回的数据中便包含了这些微小的转弯角度,由此便产生冗余的数据参数,对模型的计算结果有一定影响.经过对路径规划API返回的大量数据的分析,本文模型对转弯角度小于10°的折角予以剔除.

传统阻抗模型中转弯角度的计算往往忽略2次转弯的中间路段对阻抗的影响,但是在实际情况中,若经过一次转弯后只前进了一段极短的路程,紧接着进入下一次转弯,则整条路径的行驶代价是较大的.本文模型考虑了上述因素,计算每条路径上的转弯角度(见图2)：

(4)

式中：Ai,j表示第i个地块的中心点到第j个可达POI路径的转弯角度参数值,l为路径上的第l次的转弯,θl为第l次转弯的角度,dl表示在第l次转弯与第l-1次转弯之间的路段长度,σ为调节因子.

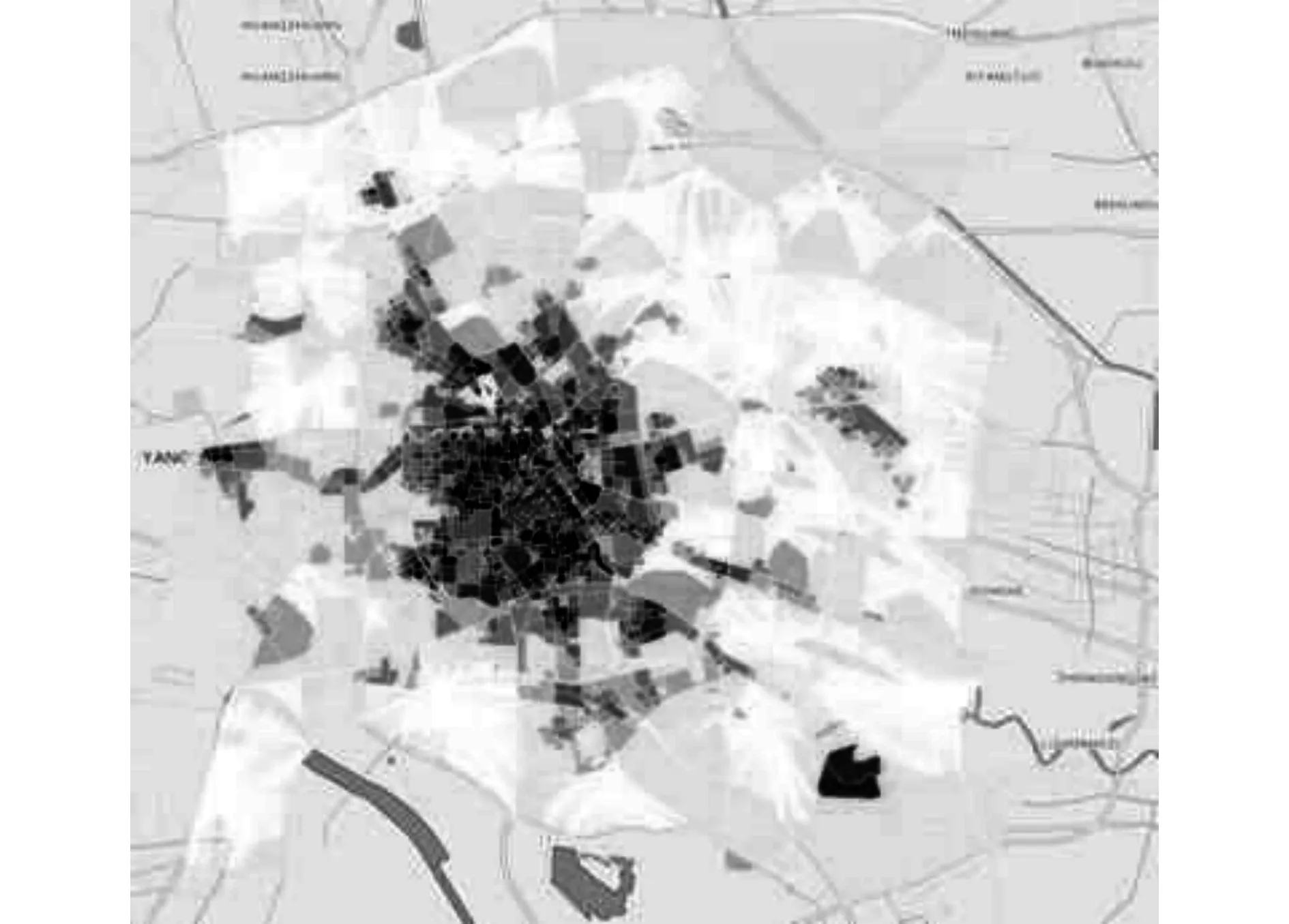
图2　天津市地块转弯角度Fig.2　Turning angle of blocks in Tianjin

图3　天津市地块转弯次数Fig.3　Turning times of blocks in Tianjin

2.3.3转弯次数在一条路径中,转弯次数同样是阻抗计算模型的重要参数,这里依旧将转弯角度小于10°的折角舍弃,并考虑相邻2次转弯间的路径长度(见图3)：

(5)

式中：Ti,j表示第i个地块的中心点到第j个可达POI路径的转弯次数参数值.

2.3.4交叉口对于路径上交叉口的阻抗函数,目前并没有公认的函数形式可以采用,但普遍认为交叉口增加路径的时间代价. 在到达POI点的路径上交叉口越多则阻抗越大；在交叉口处行进的方向不同,对应的等待时间和行驶时间也有很大不同.其中, 左转所需的代价最大,其次是直行,最小的是右转(见图4).定义交叉口参数为

(6)

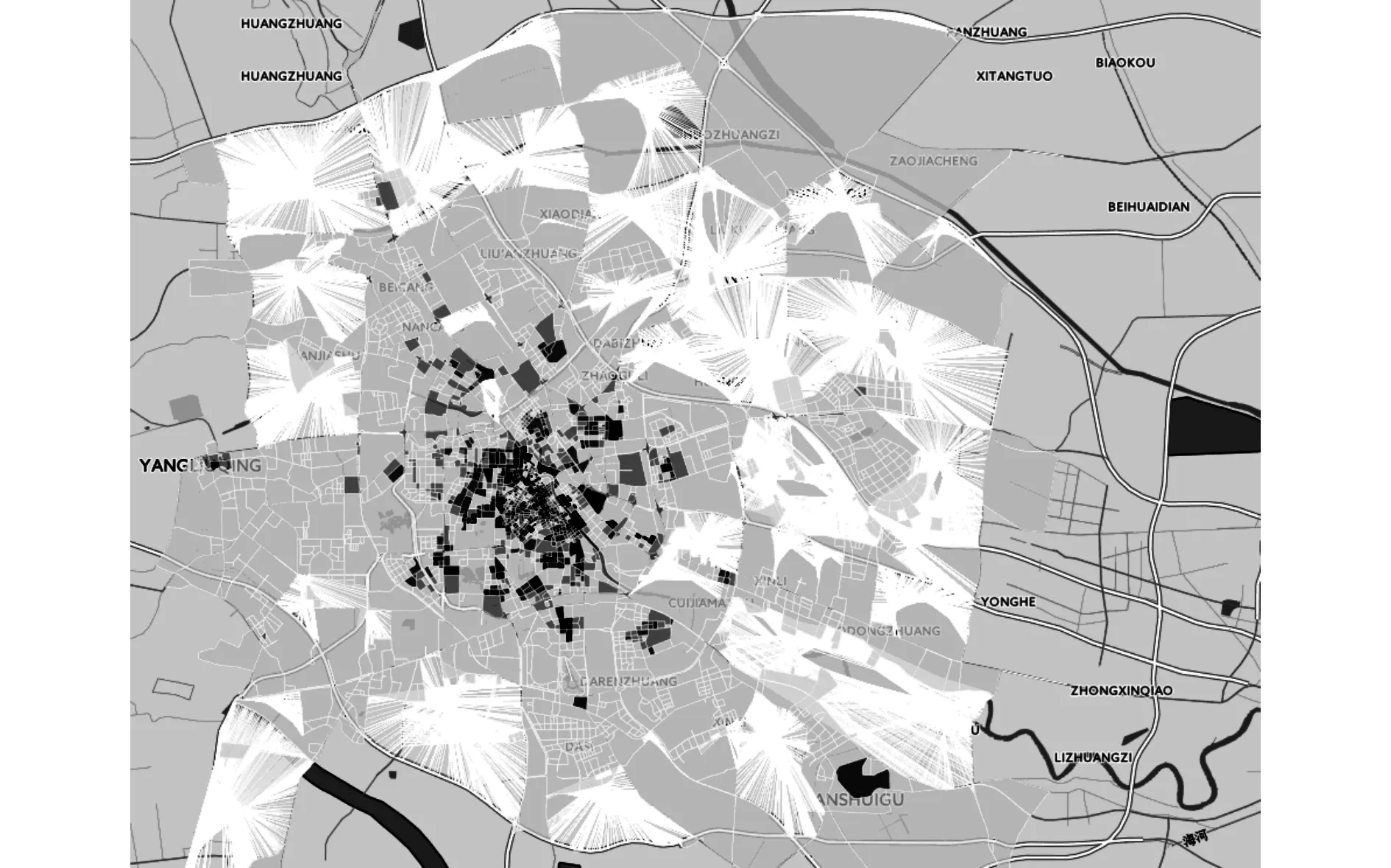
图4　天津市地块平均交叉口数量Fig.4　Average intersections of blocks in Tianjin

式中：Ii,j表示第i个地块的中心点到第j个可达POI路径的交叉口参数值；p为路径上经过的第p个交叉口；up为第p个交叉口的行进方式,包括右转、直行、左转3种方式,所对应的转弯代价系数分别为1,2,3；dp为第p个交叉口与第p-1次转弯之间的路径长度.

2.3.5人口参数一个地块在不同的时间,人口密度不同.随着人口密度直接作用于该地块的交通状况,其对阻抗的影响也自然不能忽略.在一些传统阻抗模型中,往往也考虑了人口因素,但由于城市阻抗计算对人口流动的实时性要求较高,以往的人口分布数据未必满足要求.随着社交网络的普及和快速发展,用户的签到数据对于城市人口的分布有一定的代表性,且数据能够方便地获得.因此,引入不同时间段POI点上的用户签到数据来替代传统的人口数据.此外,不同大小的地块所能承受的人口压力也不相同,考虑上述因素,将人口参数定义为

(7)

式中：Pi,t表示第i个地块在t时间段的人口参数值, ρi,t表示第i个地块在t时间段的POI总数,gj,t表示第j个POI点的在t时间段的签到总数,Si为第i个地块的面积.可视化结果如图5所示.

图5　天津市周末8:00—10:00地块人口签到密度Fig.5　Check-ins density of blocks in Tianjin from 8：00 to 10：00 during weekend

2.4计算模型

通过前文的模型参数分析,本文提出的地块分时段阻抗模型如下：

(8)

式中：Mi,t表示第i个地块在t时段的阻抗值大小.

3实验

实验采用的数据来自全国路网数据、新浪位置微博的POI兴趣点及签到数据,并采用大众点评网的POI兴趣点及签到数据作进一步验证.同时,利用传统的效用模型和潜力模型与本文提出的模型进行实验对比.

以天津市为例,通过路网数据将城市划分为2 754个地块,选取1 000m的路网距离为可达半径.采集到2014年内天津的位置微博POI点共90 731个,地块在1 000m可达半径内需要计算的POI路径共357 681条,用户在其POI点的签到数据共533 006条.

在采用的新浪位置微博POI数据中,通过POI营业时间和用户签到时间划分工作日和周末的24个时间段,利用上述阻抗计算模型,为城市地块集合{M1,M2,M3,…,Mn}分时段进行计算.Mi值越大,意味着该地块该时间段的可达阻抗越大(见图6).

图6　天津市周末8:00—10：00地块平均阻抗(基于微博POI)Fig.6　Average impedance of blocks in Tianjin during weekend from 8:00 to 10:00 (based on weibo POI)

图7　天津市周末8:00—10:00地块平均阻抗(基于大众点评POI)Fig.7　Average impedance of blocks in Tianjin during weekend from 8:00 to 10:00 (based on Dianping POI)

为验证网路兴趣点在城市阻抗计算的适用性,另采集了大众点评网的POI数据45 767条,签到数据311 794条.同样整理出周末8:00—10：00时间段营业的POI及其签到数据后,计算结果如图7所示,与微博数据计算的阻抗结果基本一致,说明本文采用网络兴趣点作为阻抗计算模型的输入有一定适用性.

在智慧城市与城市计算[20]的近期研究中,常用的阻抗模型有效用模型和潜力模型.

效用模型是基于离散选择模型的可达性度量方法,其主要思想是每个终点针对不同的起点有不同的效用值,效用值越大则到达这个终点的期望就越大,以此来衡量出行的阻抗.阻抗函数以对数和的形式予以描述：

式中：Mi指代地块i出行的阻抗,j为i可达的第j个终点,C是选择集,Vij就是j点对于i的效用值,通常采用i到j的历史OD(起讫矩阵)数为效用值.

潜力模型是以牛顿的重力模型为基础,将终点的人口数量或公共设施密集度作为吸引力加入参数考量,并引入起止点距离衰减的阻抗函数,其模型的常用表达式为

式中：Qj表示j点对i的吸引力；δ表示为距离对阻抗影响程度的指数参数,通常取值为2；dij表示i到j的距离.

图8　天津市周末8:00—10：00地块平均阻抗(效用模型)Fig.8　Average impedance of blocks in Tianjin during weekend from 8:00 to 10:00 (utility model)

图9　天津市周末8:00—10:00地块平均阻抗(潜力模型)Fig.9　Average impedance of blocks in Tianjin during weekend from 8:00 to 10:00 (gravity model)

图10　天津市周末9:00的实时路况Fig.10　Real-time road condition of weekend in Tianjin at 9:00

城市的阻抗是为了评价一定范围内人们的出行便捷程度,因此城市道路的实时路况信息能够很好地反应地块阻抗情况.本文采用百度地图的实时路况功能作为评价城市阻抗计算模型的优劣标准.如图10所示为周末9:00时天津的百度实时路况信息.线条颜色越深表示道路越拥挤，线条颜色越浅则表示道路越畅通.为了与本文的实验结果有直观的对比,通过百度地图API将天津周8:00—10:00的平均路况映射至地块后的结果图如图11所示,颜色越深表示路况越拥挤.

图11　天津市周末8:00—10:00的平均路况Fig.11　 Average road condition of weekend in Tianjin at 8:00 to 10:00

本文利用每个地块计算出的阻抗数值和路况平均值,采用闵可夫斯基距离(Minkowskidistance) 来进行相似性度量. 分别对本文提出的模型、效用模型、潜力模型与实时路况信息对比,其度量方法为

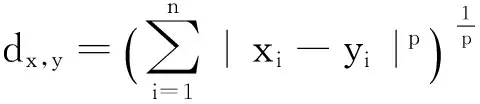
式中：x为对比的模型,y为路况信息,xi为模型计算得出的第i个地块阻抗值,yi为第i个地块的路况拥挤值,n为地块总数,此处p取值为2.

如表1、2所示分别为周末时段和工作日时段各模型与百度平均路况的相似度结果.

表1周末时段各模型与实际路况的相似度

Tab.1Similaritiesbetweenmodelsandroadconditionoverdifferenttimeperiodsduringweekend

模型闵可夫斯基距离8:00-10:0016:00-18:0020:00-22:00本文模型0.604220.753040.78652效用模型5.607146.387456.51581潜力模型2.314532.971532.74379

表2工作日时段各模型与实际路况的相似度

Tab.2Similaritiesbetweenmodelsandroadconditionoverdifferenttimeperiodsduringweekdays

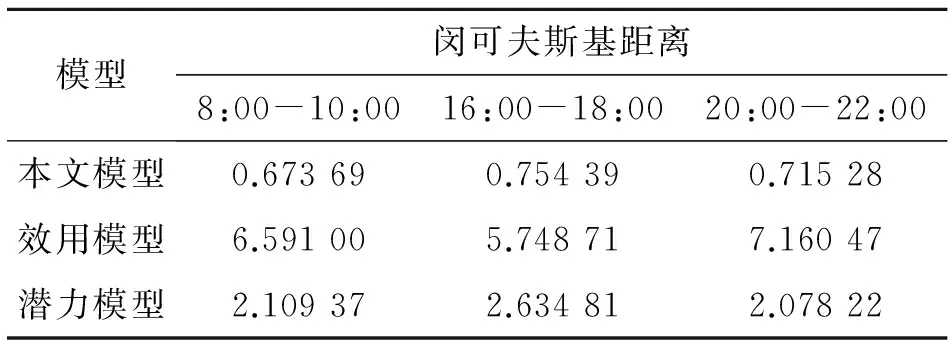
模型闵可夫斯基距离8:00-10:0016:00-18:0020:00-22:00本文模型0.673690.754390.71528效用模型6.591005.748717.16047潜力模型2.109372.634812.07822

通过各模型的结果图和实时路况结果图对比以及表1、2三个典型时间段的各模型相似度对比,结果表明：本文提出的阻抗计算模型(见图6)的结果与路况信息较为相符,潜力模型(见图8)次之,效用模型(见图9)的计算结果较为不符.这是因为效用模型只考虑了终点处对起点处的吸引力,而忽略了对两点之间路径情况的分析；潜力模型虽然加入了路程中距离衰减的阻抗函数,但考虑参数不足.

本文模型结合地块与兴趣点间的路网距离、转弯角度、转弯次数、交叉口及人口等因素,能较真实地反映出不同时间段城市的阻抗情况.

4结语

本文构建了一个基于移动社交网络兴趣点的城市阻抗计算模型.其中城市基本地块信息通过路网数据获得,兴趣点及签到数据利用位置微博获得,道路情况通过百度地图API的路线交通规划方法获得,以此替代传统阻抗模型的道路路线信息及人口出行数据.通过实验对比分析验证了模型的可行性.文中对于到兴趣点的路线规划只提取最短的路径,尚未考虑多路径的情况.后续工作将进一步分析阻抗的影响因素,并加入如移动设备的基站数据等其他类型的数据,提供进一步的计算模型.

参考文献(References)：

[1]BAHRLEM.Accessibility:insearchofaunifiedtheory[J].EnvironmentandPlanningBPlanningandDesign, 2009, 36(2): 191-194.

[2]YANGS,LIUX,WUYJ,etal.Canfreewaytrafficvolumeinformationfacilitateurbanaccessibilityassessment？CasestudyofthecityofSt.Louis[J].JournalofTransportGeography, 2015, 44: 65-75.

[3] 尹鹏,李诚固,陈才.东北地区省际城市可达性及经济联系格局[J].经济地理, 2014,34(6): 68-74.

YINPeng,LICheng-gu,CHENCai.Inter-provincialaccessibilityandeconomiclinkagespatialpatterninNortheastChina[J].EconomicGeography, 2014, 34(6): 68-74.

[4]WUSJ,SHIQX,LUHP.Reviewoferrorstructureextensionofdiscretechoicemodelsintravelmodechoice[J].HighwayEngineering, 2007,32(6): 92-97.

[5]KWAN,MP.Genderandindividualaccesstourbanopportunities:astudyusingspace-timemeasures[J].ProfessionalGeographer, 2010, 51(2): 211-227.

[6]DURAN-FERNANDEZR,SANTOSG.AregionalmodelofroadaccessibilityinMexico:accessibilitysurfacesandrobustnessanalysis[J].ResearchinTransportationEconomics, 2014, 46: 55-69.

[7]WELCHTF.Equityintransport:thedistributionoftransitaccessandconnectivityamongaffordablehousingunits[J].TransportPolicy, 2013, 30: 283-293.

[8] 刘灿齐.现代交通规划学[M].北京：人民交通出版社,2001: 98-102.

[9]WILSONAG.Complexspatialsystems:themodellingfoundationsofurbanandregionalanalysis[J].ComplexSpatialSystemstheModellingFoundationsofUrbanandRegionalAnalysis, 2000, 36(4): 446-446.

[10] 刘彤,巩丽媛,薛运强,等.指数型阻抗函数的双约束引力模型[J].科学技术与工程,2009(21):6279-6282.

LIUTong,GONGLi-yuan,XUEYun-qiang,etal.Studyondoubleconstraintgravitymodelofexponentialimpedancefunction[J].SciencetechnologyandEngineering, 2009(21): 6279-6282.

[11]DOMENICHINIL,SALERNOG,FANFANIF,etal.Traveltimeincaseofaccidentpredictionmodel[J].Procedia-SocialandBehavioralSciences, 2012, 53: 1078-1087.

[12]VOJKOVICG,KATULICT.Onthedegradationofperformancefortrafficnetworkswithoblivioususers[J].TransportationResearchPartBMethodological, 2011, 45(2): 364-371.

[13]WOENSELTV,CRUZFRB.Astochasticapproachtotrafficcongestioncosts[J].ComputersandOperationsResearch, 2009, 36(6): 1731-1739.

[14]WANGYQ,ZHOUW,LULE.Theoryandapplicationstudyoftheroadtrafficimpedancefunction[J].JournalofHighwayandTransportationResearchandDevelopment, 2004, 21(9): 82-85.

[15]HEN,LIUN,ZHAOSC.Astudyofroadtrafficimpedancebaseonbprfunction[J].JournalofNanjingInstitudeofTechnology:NaturalScienceEdition, 2013,11(1): 6-11.

[16]YUANNJ,ZHENGY,XIEX.Segmentationofurbanareasusingroadnetworks[R]. [S.l.]:MicrosoftTechnicalReport, 2012.

[17]YUANJ,ZHENGY,XIEX.DiscoveringregionsofdifferentfunctionsinacityusinghumanmobilityandPOIs[C]∥Proceedingsofthe18thACMSIGKDDinternationalconferenceonKnowledgediscoveryanddatamining.Beijing:ACM, 2012: 186-194.

[18] 王京京, 杨友林, 李辉,等. 基于功能分析的城市道路网络衔接评价研究 [J]. 交通运输系统工程与信息, 2015, 15(1): 212-217.

WANGJing-jing,YANGYou-lin,LIHui,etal.Urbanroadnetworkjunctionevaluationmethodbasedonthefunctionalanalysis[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2015, 15(1): 212-217.

[19]CartDB. [2015-12-20].http:∥cartodb.com/.

[20]ZHENGY,CAPRAL,WOLFSONO,etal.Urbancomputing:concepts,methodologies,andapplications[J].ACMTransactionsonIntelligentSystemsandTechnology, 2014, 5(3): 222-235.

收稿日期：2015-12-28.

基金项目：国家自然科学基金青年资助项目(61300104);国家自然科学基金青年资助项目(61300103);福建省教育厅科技重点资助项目(JK2012003);福建省科技厅产学重大资助项目(2014H6014); 福建省自然科学基金资助项目(2013J01230).

作者简介：郑松潘(1990—)，男，硕士生，从事复杂网络、数据挖掘研究. ORCID: 0000-0001-8301-4413.E-mail: zhengsongpan@163.com 通信联系人：於志勇，男，讲师.ORCID: 0000-0002-2051-9462. E-mail: yuzhiyong@fzu.edu.cn.

DOI:10.3785/j.issn.1008-973X.2016.06.025

中图分类号：TP 391

文献标志码：A

文章编号：1008-973X(2016)06-1189-07

Urbanimpedancecomputingmodelbasedonpointsofinterest

ZHENGSong-pan1,2,CHENYu-zhong1,2,YUZhi-yong1,2,GUOSong-rong1,2,SHENYao3

(1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350108, China; 2. Fujian Key Laboratory of Network Computing and Intelligent Information Processing, Fuzhou University, Fuzhou 350108, China;3. Space Syntax Laboratory, Bartlett School of Architecutre, University College London, LondonNW12BX, UK)

Abstract:An urban impedance computing model was proposed based on the points of interest from social networks for real-time calculation of urban impedance. The model used the land blocks divided by urban traffic networks as the basic units, and factors such as the average traffic distance, turning angle, turning times, intersection and the population and so on were considered to calculate the urban impedance within an accessible radius. In the experiment, the urban impedance was calculated for each 2 h using the proposed model, and was compared with the utility model and the gravity model. The results show that the similarity between our impedance model and the actual road situation is 80% higher than the utility model and 60% higher than the gravity model, respectively. The proposed model improves the applicability of urban impedance calculation and reflects the variation in different time periods.

Key words:urban accessibility; impedance computing; points of interest (POI); check-ins; smart city