球面网壳地震动输入与振型响应的相关性
相 阳, 罗永峰, 廖 冰, 沈祖炎
(1. 同济大学 建筑工程系,上海 200092; 2. 上海同济建设工程质量检测站,上海 200092)
球面网壳地震动输入与振型响应的相关性
相阳1, 罗永峰1, 廖冰2, 沈祖炎1
(1. 同济大学 建筑工程系,上海 200092; 2. 上海同济建设工程质量检测站,上海 200092)
摘要:通过分析球面网壳结构对预定地震荷载谱的响应,选出对结构反应贡献较大的主振型(DM)并用于振型叠加计算,提高振型叠加法(MSM)的计算效率.为获得球面网壳在预定地震荷载谱作用下的响应规律以及研究结构振型响应与地震动输入的相关性,基于准静力响应、共振响应及耦合响应的定义,计算结构在预定地震动输入功率谱作用下的位移响应谱、准静力响应谱、共振响应谱及耦合响应谱,得出各响应分量对总响应的贡献规律.结果表明,在预定地震动输入下,球面网壳结构响应主要由某一个或几个特定频率区段的振型响应控制,在不同的频率区段,对总响应贡献最大的响应分量类型不同.给出在预定地震动区划和场地条件下,考虑地震动输入与结构响应相关性的改进振型叠加法的分析流程.
关键词:球面网壳;地震动输入;振型响应;主振型
网壳结构自由度多,振型数量庞大且振型复杂.采用振型叠加法计算网壳结构地震反应常存在质量参与系数累积慢、振型截断误差大等问题[1-2].我国现行《空间网格结构技术规程》(JGJ7-2010)[3]规定,当采用振型分解反应谱法进行空间网格结构地震作用效应分析时,对于网壳结构宜至少取前25~30个振型,以进行效应组合.然而,这一振型截取数往往并不能满足分析精度要求[4-6].《空间网络结构技术规程》虽对体型复杂或重要的大跨度空间网格结构补充建议截取更多振型进行效应组合,但并未给出参与组合振型的明确数目和遴选原则.实际结构分析表明,当以质量参与系数累计值为控制指标进行振型叠加分析时,往往需要组合前上百阶甚至数百阶振型才能满足要求,导致分析效率很低.鉴于此,国内外学者为减少振型叠加法所需考虑的振型数进行了诸多研究.Wilson等[7-8]提出并发展了荷载相关Ritz向量法,使得分析选用的振型中不包含与荷载空间分布模式相似程度低甚至正交的振型,分析效率得以明显提高.王磊等[9-10]依据振型静力功、动力功参与系数遴选结构主振型,克服了应用质量参与系数指标时振型反应累积速度慢的问题.
目前,应用于空间网格结构地震反应分析的振型遴选方法,普遍未考虑地震动输入与结构自身动力特性的相关性,这使得结构地震反应分析中须考虑的振型数依然较多.随着实际地震动记录数量的累积、地震地面运动模拟方法的发展以及对局部场地动力特性的了解,我国地震烈度区划图即将被地震动区划图取代[11].在这一背景下,对于重要的大型空间网格结构,在地震反应分析中考虑结构振型响应与地震动输入的相关性,即对一定频谱特性的地震动,计算出对结构响应贡献大的振型并将其用于振型叠加计算,可进一步减少分析所需的振型数量以提高效率.
结构动力反应与动力激励的相关性研究多存在于风工程领域.Davenport[12]基于脉动风荷载这一典型动力荷载,提出了背景响应和共振响应的概念,即结构响应谱可分为2个组成部分:一部分形状与风压谱形状相同,体现脉动风的准静力作用,定义为背景响应;另一部分为结构自振频率附近的响应谱尖峰,体现了因结构惯性力产生的动力放大效应,定义为共振响应.随后,Davenport[13]发展了该理论,在时域内重新定义了背景响应和共振响应.基于此概念,结构的风振响应参与振型得以确定,风振响应分析效率明显提高.陈波等[14]给出了结构风振响应分析中背景响应、共振响应及其相关性的严格定义及计算方法,该定义可被扩展至空间网格结构的地震响应划分,并可在给定地震动区划或地震动荷载谱的情况下,进一步计算各响应分量对总响应的贡献,得到对结构总响应贡献较大的振型频率分布域,进而使振型叠加分析所需要的主振型数量得以缩减.
本文基于上述理论方法给出一致激励地震地面运动的随机过程描述方法,参照风振响应分析中背景响应、共振响应及其相关性的定义,导出结构地震响应中准静力分量、共振分量及耦合分量的计算公式,并提出考虑输入与响应相关性的改进振型叠加法分析流程.依据3组实际地震动记录,生成3组地震动输入功率谱,并将其用于球面网壳结构的地震响应分析.通过对球面网壳准静力响应、共振响应及耦合响应的分析计算,获得结构各响应分量对总响应贡献程度的分布规律,并分析各分量主要贡献振型的频率分布域,为进一步遴选主振型、缩减主振型数量提供依据.
1地震作用的随机过程描述
在支座一致激励输入和空间三维平动输入的条件下,结构各节点在某时刻的惯性力取决于该点的质量,因此,与脉动风作用不同,结构各节点的地震作用在空间上是确定相关的,地震作用仅仅是关于时间t的随机过程.任一点的地震作用和结构地震作用的协方差矩阵可分别表示为
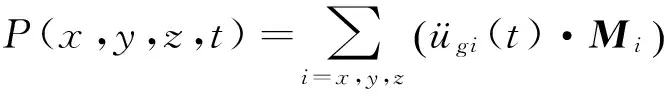
(1)
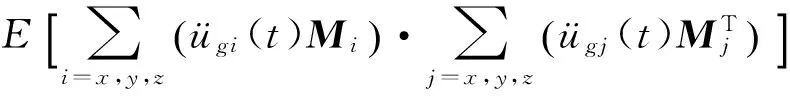
(2)
式中:P(x,y,z,t)为坐标(x,y,z)处的节点于t时刻所受的地震作用,ügi(t)为t时刻i方向地面加速度,Mi(i=x,y,z)为节点三向平动质量构成的矢量.CP为地震作用协方差矩阵.
假设空间三向地面运动互不相关,即假定不同方向地面加速度随机过程的互协方差E[ügi(t)· ügj(t)](i≠j)为零,则矩阵CP表示为

(3)


(4)
式中:j为结构节点号,J为节点总数,Mji即节点j在i方向的质量.式(4)说明,结构质量分布向量可作为地震作用协方差矩阵CP的特征向量,即Mi(i=x,y,z)可作为描述结构地震作用分布形式的基向量.结构地震作用随机过程可以用一组关于时间t的随机函数(地面加速度时程)和一组确定的基向量(结构质量分布)的乘积表示[15].结构中任一节点k的地震作用均方差可以进一步表示为
(5)
对特定地震动区划,选取一定数量统计特征相近的地震动记录,经集合平均,即可由式(5)计算得到结构的地震作用均方差.当然,地震作用均方差也可由一定地震动区划的地震动功率谱,经Fourier逆变换得到.
2准静力响应及共振响应时、频域表达
2.1时域内准静力响应、共振响应
自由度为N的多自由度体系位移响应可表示为
u(t)=u(t)I+u(t)S=
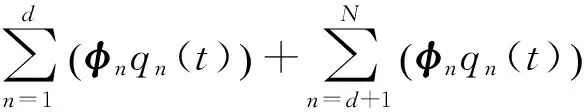
(6)
式中:u(t)I和u(t)S分别为主振型(考虑共振效应)的及非主振型(忽略共振效应)的位移响应,d为主振型数,n为振型阶次,φn、qn(t)分别为结构振型和振型正则坐标位移响应.
非主振型位移响应qSn(t)可由静力方法求得,即

(7)
式中:P(t)、K为外荷载向量和结构刚度矩阵,Pn(t)、Kn为第n阶非主振型的广义力和广义刚度.

u(t)Sn=φnqSn(t)=FnP(t).
(8)
非主振型的静力贡献之和可由结构总静力反应与主振型静力贡献之差给出,即

(9)
将式(9)代入式(6),结构总位移响应反应可表达为

(10)
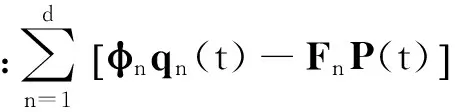
2.2频域内准静力响应、共振响应及耦合响应
结构主振型与非主振型对结构地震响应的贡献可由时域范围内准静力响应及共振响应的定义直接给出.计算结构反应尚须预先确定结构的主振型.由于运用荷载相关Ritz向量法或阈值法求解出的结构主振型数量较多,考虑结构反应与预定地震动输入之间的相关性,分析各振型反应分量对结构总反应的贡献大小以缩减主振型数量很有必要.显然,这一过程应在频域范围内展开,故应在频域范围内定义并计算准静力响应、共振响应及耦合响应.
2.2.1准静力响应、共振响应的频域表达由式(7)、(8)可得第n阶振型的准静力响应为
u(t)Sn=φnqSn(t)=φnPn(t)/Kn.
(11)
将动力荷载的功率谱密度函数表示为Spnpm(ω),则结构响应准静力分量的功率谱密度函数矩阵可表达为

(12)
式中:ω为圆频率,m为振型阶次;m≠n.去掉复频反应函数Hn(ω)中的静力反应分量,可得到共振响应的频响传递函数:

(13)
式中:ξn、ωn分别为第n阶振型的阻尼比和圆频率.
结构共振响应分量的功率谱密度函数矩阵为

(14)

2.2.2耦合响应的频域表达各阶振型响应准静力分量与共振分量的互相关函数为
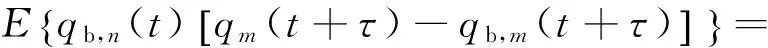
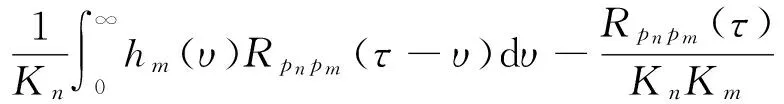
(15)
式中:hm(υ)为脉冲响应函数,Rpnpm(τ)为振型间动荷载的互相关函数,τ为时间间隔.对于稳态响应,式(15)中积分下限可延伸至负无穷[16],在此基础上进行Fourier变换,可得到结构振型之间准静力分量和共振分量的互功率谱密度函数Sqb,nqr,m(ω),即

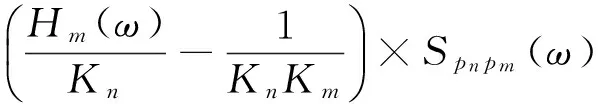
(16)
由此,结构振型响应准静力分量与共振分量之间的互功率谱密度函数矩阵可表达为
(17)
2.2.3结构位移总响应结构各振型响应之间的互相关函数为

Rqb,nqb,m(τ)+Rqb,nqr,m(τ)+Rqr,nqb,m(τ)+Rqr,nqr,m(τ).
(18)
对式(18)进行Fourier变换,可得到各振型响应之间的互功率谱密度函数[17],即
Sqnqm(ω)=Sqb,nqb,m(ω)+Sqb,nqr,m(ω)+
Sqr,nqb,m(ω)+Sqr,nqr,m(ω) .
(19)
式(19)等号右侧第一项为准静力分量振型响应谱,中间2项为准静力分量和共振分量耦合振型响应谱,最后一项为共振分量振型响应谱.故依据结构振型响应的振型展开式
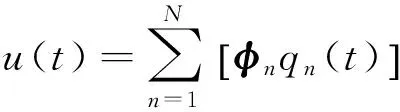
(20)
将结构总响应表达为各振型反应的叠加时,结构总响应的功率谱密度函数矩阵可表示为

(21)
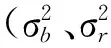
(22)

(23)

(24)
式(22)、式(23)和式(24)中:γnx为第n阶振型在x方向地震作用下的振型参与系数,ωA、ωB分别为地震作用能量分布频域的下、上限.结构总响应均方差为

(25)
式中:CR为互协方差Cb,r和Cr,b的实部.
若同时考虑空间三维地震作用,可将各方向地震作用功率谱的稳态响应进行叠加,但需要考虑不同方向地震作用间的互功率谱函数.
2.2.4结构内力响应求得结构位移响应谱后,可进一步推导出结构的内力响应谱.t时刻结构的弹性恢复力可表示为

(26)

(27)
式中:δrT为结构响应的柔度函数,可根据所需的内力响应具体计算.由于结构振型满足下述方程
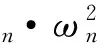
(28)
式(27)可进一步表达为

(29)式中:Pdn和an分别为振型惯性力和对应的结构响应:
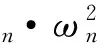
(30)

(31)
式(29)中r(t)表示结构某单个自由度的响应,当计算多个自由度的内力响应时,可采用向量表达

(32)
式(32)与式(20)形式类似.将式(20)中的振型向量φn用响应向量An代替,结合式(21),可得结构的内力总响应谱[16]

(33)
结构内力的准静力响应谱、共振响应谱及耦合响应谱可通过将式(12)、(14)和(17)中的φn、Hn,r(ω)分别替换为An、Hn(ω)得到,限于篇幅,不再列出其具体表达式.
3考虑响应与激励相关性的分析方法
基于以上论述,在预定地震动区划下,结合局部场地特性,可选定多条地面加速度时程或人工地震波,利用式(5)并结合Fourier变换,可求得结构地震作用功率谱.将地震作用功率谱进行集合平均,可得到结构地震作用的频谱特性.按上述方法,分析结构各振型各响应分量在此预定地震作用下的响应幅度,即可考察结构的准静力响应谱、共振响应谱和耦合响应谱对总响应的贡献程度.通过各响应分量的功率谱密度,可得到对结构总响应贡献较大的振型频率分布域[ωL,ωR].在此频率域范围内,结合荷载相关Ritz向量法或振型遴选阈值法,选择结构主振型进行结构地震反应分析,可缩减结构主振型数量.具体分析流程如下:1)基于地震动区划及场地条件,选定一批地震动记录或生成人工地震波;2)对地震动功率谱进行集合平均,得到分析用地震作用功率谱密度函数;3)分析结构自振特性,在频域内计算结构各响应分量及总响应;4)根据结构响应谱选定主振型频率域,在主振型频率域内计算Ritz振型或依据阈值法遴选主振型;5)针对主振型在时域或频域内进行结构地震响应的振型叠加分析,得结构地震反应.
需要说明的是,主振型频率分布域可由若干段频率域的并集构成,即
(34)
由于在频域计算结构各响应分量的功率谱耗时很短,对于网壳结构,采用考虑地震动输入与结构响应相关性的振型叠加法分析结构地震反应可明显提高计算效率.
4球面网壳地震输入与响应相关性算例
本节通过网壳结构算例说明地震动输入与结构振型响应的相关性.限于讨论结构响应与地震输入的相关性,未给出基于输入与响应的相关性缩减主振型数量以及对结构进行振型叠加地震反应分析的计算内容.
算例为Kiewitt6型钢网壳,跨度L=60 m,矢高h=12 m,杆件为Φ150.0 mm×4.0 mm钢管,弹性模量取Es=2.06×105MPa,网壳屋面荷载取0.05 kN/m2,约束网壳最外环节点所有自由度.网壳结构如图1所示,结构基本周期为0.275 6 s,各阶振型自振圆频率ω如图2所示.
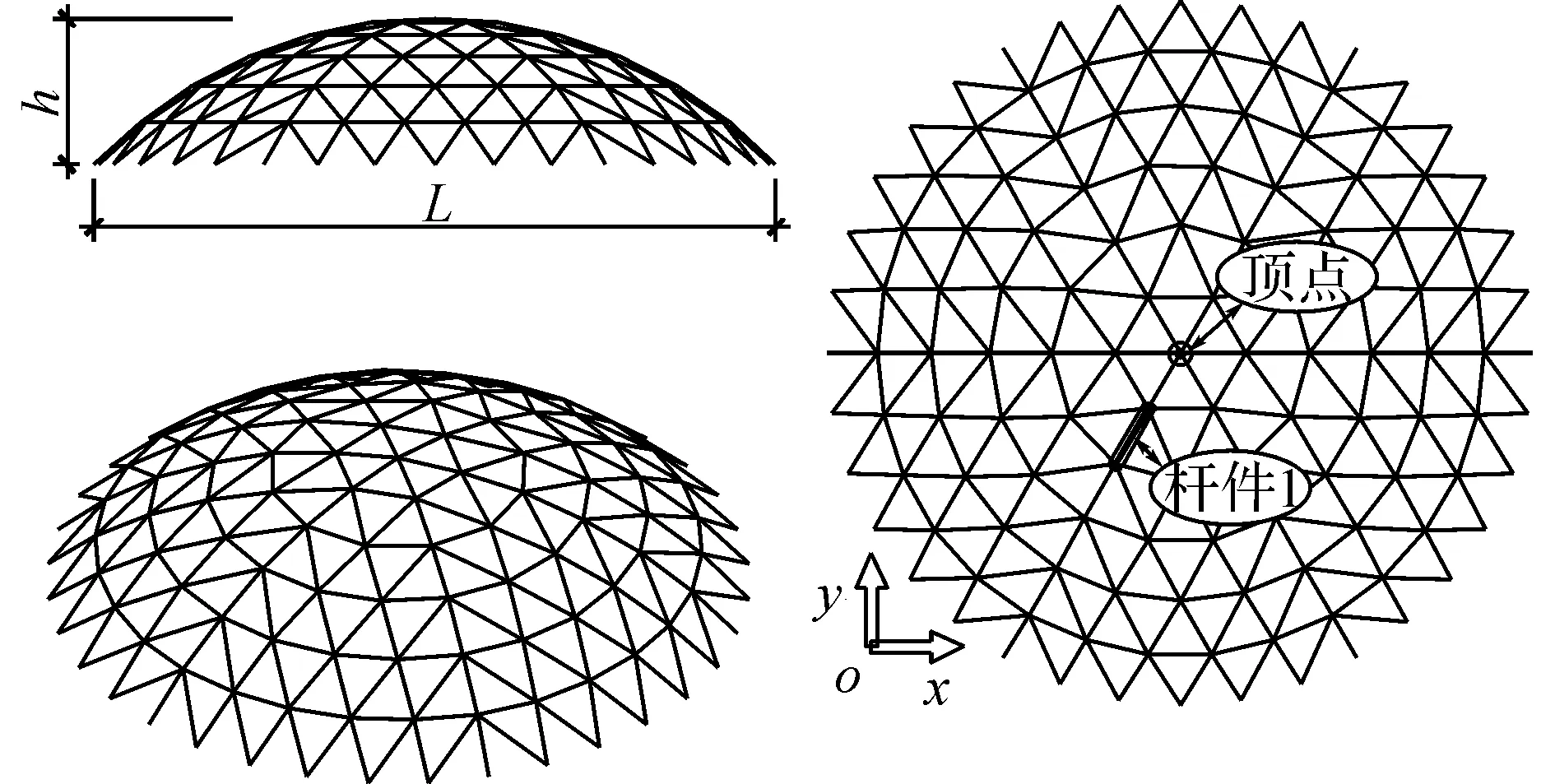
图1 Kiewitt 6球面网壳Fig.1 Kiewitt 6 spherical latticed shell

图2 球面网壳自振圆频率Fig.2 Circular frequency of vibration modes of spherical latticed shell
4.1地震动输入功率谱
取场地条件类似地区的多条x、y、z向强震记录样本曲线,将样本谱进行集合平均,作为地震动加速度荷载功率谱.
本算例所采用的地震动荷载谱包括:28条美国加州地震动记录集合平均功率谱APS1;12条日本地震动记录集合平均功率谱APS2;2条墨西哥地震动记录集合平均功率谱APS3. 3组地震动记录的集合平均功率谱密度(power spectrum density, PSD)如图3所示.

图3 地震动输入功率谱密度Fig.3 Power spectrum density of seismic input
4.2球面网壳各类响应主要贡献振型的频域分布
4.2.1结构位移响应按照本文给出的响应分量的谱分析方法,分别计算3组地震功率谱作用下球面网壳的位移响应谱、准静力响应谱、共振响应谱和耦合响应谱以及稳态响应均方差,计算得到网壳顶点位移的响应谱如图4所示.
对于地震作用功率谱ASP1(美国),网壳顶点位移响应谱的低频段(ωn≤20.0)主要为准静力响应分量,高频段(20.0≤ωn≤30.0)主要为共振响应分量,其中z向总位移响应谱的高频成分与共振分量响应谱几乎完全一致,耦合响应谱值较大的频率域也主要分布在共振响应明显的区域.
对于地震作用功率谱ASP2(日本),网壳顶点位移响应谱的低频成分(7.5≤ωn≤20.0)主要来自准静力响应分量,高频成分(20.0≤ωn≤26.5)则明显来自共振响应分量,而耦合响应谱较大的频率域主要集中在共振响应明显的区域,共振响应分量对结构总响应起控制作用.
在ASP1(美国)和ASP2(日本)地震动输入下的结构总响应中,准静力分量和耦合分量贡献之和约占10%.其中,耦合分量贡献值约为准静力分量的2倍.对于地震作用功率谱ASP3(墨西哥),结构响应完全集中在以准静力响应为主的低频(2.0≤ωn≤3.5)范围内,耦合响应约占总响应的5%,共振分量小于1%.
由分析结果可见,在选定地震动输入功率谱的条件下,网壳结构位移响应谱值较大的频率域存在明显的分段现象,即结构响应主要由某一个或几个特定频率区段的振型响应控制,且在不同频率区段内,对总响应贡献最大的振型响应分量类型不同.
4.2.2结构内力响应按照第2.2.4节的内力响应谱计算方法,以美国加州地区的地震动输入功率谱ASP1为例,针对网壳结构x、z向的支座总反力和杆件1(见图1)的轴力,分别计算其总响应谱、准静力响应谱、共振响应谱和耦合响应谱,如图5所示.
由分析结果可见,对于网壳结构各内力响应,低频成分基本为准静力分量,高频成分则为共振分量.内力响应谱的峰值分布与位移响应谱相比更为分散,峰值数量更多,特别是z向支座反力总响应谱,存在多个峰值.而x向支座反力响应谱的能量主要分布频域(20.0≤ωn≤30.0),与位移响应谱基本一致.杆件1轴力的总响应则由共振响应控制.

图4 球面网壳顶点位移响应谱Fig.4 Displacement response spectra of central node of spherical latticed shell

图5 球面网壳结构内力响应谱Fig.5 Structural force response spectra of spherical latticed shell
由上述对网壳顶点位移响应谱及杆件轴力响应谱的分析可见,结构响应与地震动输入之间存在明显的相关性.考虑地震动输入特性,在响应的主要频段内选择结构主振型,可自动滤掉对结构响应贡献小的振型,进而可减少结构地震反应分析需要组合的振型数量.
5结语
在时域范围内,球面网壳结构的地震反应可由主振型的共振响应和结构整体的准静力响应组合得到,在此基础上,可导出结构频域范围内振型响应准静力分量、共振分量和耦合分量的计算方法.对应预定地震区划和场地条件,计算地震动输入功率谱作用下的结构响应谱,可获得结构响应谱值较大的频率区段及对应的振型响应类型,进而得出结构主振型的频率范围.按照本文给出的分析流程,应用振型叠加法分析球面网壳结构地震反应,可提高计算效率.
本文理论推导中,假定空间三向地面运动互不相关,即假定三向地面加速度随机过程的互协方差为0,若选定合理的地面运动互协方差模型并纳入理论推导,则本文方法可进一步完善.
参考文献(References):
[1] 廖冰,罗永峰,王磊,等.基于质量参与系数的空间结构动力模型简化[J].湖南大学学报:自然科学版, 2013, 40(9): 7-13.
LIAO Bing, LUO Yong-feng, WANG Lei, et al. A new simplified method for the dynamic model of spatial structures based on mass participation factors [J]. Journal of Hunan University: Natural Science, 2013, 40(9): 7-13.
[2] 廖冰,罗永峰.基于振型贡献系数的空间结构振动反应研究[J].空间结构,2014, 20(1): 9-17.
LIAO Bing, LUO Yong-feng. Vibration response computation of spatial structures based on mode contribution factors [J]. Spatial Structures, 2014, 20(1): 9-17.
[3] 中华人民共和国住房和城乡建设部.空间网格结构技术规程:JGJ 7-2010[S]. 北京: 中国建筑工业出版社, 2010: 21-23.
[4] 胡仲淹,罗永峰,王人鹏,等.基于振型遴选与振型构造的空间网格结构动力分析方法[J].工业建筑, 2015, 45(1): 16-22.
HU Zhong-yan, LUO Yong-feng, WANG Ren-peng, et al. The dynamic analysis of spatial lattice structures based on mode selection and mode construction techniques [J]. Industrial Construction, 2015, 45(1): 16-22.
[5] YIN Y, HUANG X, HAN Q, et al. Study on the accuracy of response spectrum method for long-span reticulated shells [J]. International Journal of Space Structures, 2009, 24(1): 27-35.
[6] 吴雨杭,尹越,刘璐.空间网格结构振型分解反应谱分析合理振型数研究[J].空间结构, 2015, 21(4): 25-31.
WU Yu-hang, YIN Yue, LIU Lu. Reasonable mode number required in mode superposition response analysis for space frame structures [J]. Spatial Structures, 2015, 21(4): 25-31.
[7] WILSON E L, YUAN M W, DICKENS J M. Dynamic analysis by direct superposition of Ritz vectors [J]. Earthquake Engineering and Structural Dynamics, 1982, 10(6): 813-821.
[8] GU J, MA Z D, HULBERT G M. A new load-dependent Ritz vector method for structural dynamics analyses: quasi-static Ritz vectors [J]. Finite Elements in Analysis and Design, 2000, 36(3): 261-278.
[9] 王磊,罗永峰.空间网格结构抗震分析中的阈值法理论[J].东南大学学报:自然科学版,2011, 41(3): 636-641.
WANG Lei, LUO Yong-feng. Threshold vaule method in seismic analysis of spatial latticed structures [J]. Journal of Southeast University: Natural Science Edition, 2011, 41(3): 636-641.
[10] LUO Y F, WANG L, GUO X N. Threshold value method and its application in dynamic analysis of spatial latticed structures [J]. Advances in StructuralEngineering, 2012, 15(12): 2215-2226.
[11] 李英民,刘立平.工程结构的设计地震动[M].北京:科学出版社, 2011: 14-15.
[12] DAVENPORT A G. Gust loading factors [J]. Journal of the Structural Division, 1967, 93(3): 11-34.
[13] DAVENPORT A G. How can we simplify and generalize wind loads? [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54: 657-669.
[14] 陈波,武岳,沈世钊.背景响应,共振响应定义及其相关性分析方法[J].振动工程学报, 2008, 21(2): 140-145.
CHEN Bo, WU Yue, SHEN Shi-zhao. Definitions and correlation analyses for background response and resonant response [J]. Journal of Vibration Engineering, 2008, 21(2): 140-145.
[15] 廖冰.大跨度空间结构主振型遴选与地震作用相关性研究[D].上海: 同济大学, 2014.
LIAO Bing. Dominate vibration mode selection and correlation between the dominate vibration mode and seismic action in large-span spatial structures [D]. Shanghai: Tongji University, 2014.
[16] 俞载道,曹国敖.随机振动理论及其应用[M].上海: 同济大学出版社, 1988: 243-247.
[17] 廖冰,罗永峰.大跨度空间结构地震响应组成分量研究[J].工业建筑, 2015(2): 107-113.
LIAO Bing, LUO Yong-feng. Research on seismic response components of large-span spatial structures [J]. Industrial Construction, 2015(2): 107-113.
收稿日期:2015-04-11.
基金项目:国家自然科学基金资助项目(51378379).
作者简介:相阳(1988—),男,博士生,从事大跨度空间结构地震反应分析方法研究. ORCID: 0000-0002-3589-5436. E-mail: 001_xiangyang@tongji.edu.cn 通信联系人:罗永峰,男,教授,博导. ORCID: 0000-0001-8212-5605. E-mail: yfluo93@tongji.edu.cn
DOI:10.3785/j.issn.1008-973X.2016.06.005
中图分类号:TU 391
文献标志码:A
文章编号:1008-973X(2016)06-1040-08
Correlation between seismic input and modal response of spherical latticed shell
XIANG Yang1, LUO Yong-feng1, LIAO Bing2, SHEN Zu-yan1
(1.DepartmentofBuildingEngineering,TongjiUniversity,Shanghai200092,China;2.ShanghaiTongjiConstructionQualityInspectionStation,Shanghai200092,China)
Abstract:The dominant modes (DM) of latticed shells was obtained by analyzing the modal response characteristics in accordance with the pre-determined earthquake excitation input in the frequency domain, and the efficiency of the modal superposition method (MSM) was improved. The modal response characteristics were obtained by calculating the numerical values of the modal quasi-static response, and the resonant response and the coupled response after their definitions were given. The correlation between the earthquake excitation input and the modal response was studied. The regularities of the component responses contributing to the overall responses were obtained as well. Numerical examples show that the DM frequencies are controlled by a certain frequency range or several certain frequency ranges in accordance with the predicted excitation input. For the different frequency ranges of the total structural response, the type of the dominant modal response varies. Meanwhile, the procedure of the modified MSM was given, which takes the correlation between the structural responses and the seismic input under certain seismic zonation and site condition into consideration.
Key words:spherical latticed shell; seismic excitations; modal response; dominant mode

