彰显“种子课”的力量
——“长方形和正方形的认识”教学实录与思考
◇洪菲菲
彰显“种子课”的力量
——“长方形和正方形的认识”教学实录与思考
◇洪菲菲

课前思考
学生在一年级时已经初步认识了长方形和正方形,生活中也积累了很多关于长方形和正方形的认知经验,对这两种平面图形可谓非常熟悉。那么,这节课的价值在哪儿?深入解读教材及分析学情之后我发现,学生虽然对这两种平面图形很熟悉,但这种认识还处于“直观辨认水平”,对学生而言深入研究图形还是“第一次”。换言之,这是一节“种子课”,对后续各种平面图形的认识有着重要的作用。本节课的教学将为学生积累探究图形特征的经验,使学生在学习中能够主动捕捉观察视角、掌握探究方法、感悟图形关系,这些能力将成为他们后续学习的强劲动力。
教学过程

(黑板上出示任意四边形、三角形、梯形、圆、长方形、正方形、平行四边形等平面图形)
师:咱们来比比谁的眼睛亮。黑板上有许多图形,你们能不能把长方形和正方形快速地找出来?
(学生找出若干个长方形和正方形)
师:看来,找长方形和正方形对你们来说很容易。与其他图形相比,长方形和正方形有什么不一样的地方呢?谁来说一说?
生:长方形左右2条边一样长,上下2条边一样长。正方形的4条边都一样长。
生:长方形和正方形的4个角都是直角。
师:看来,长方形和正方形在边和角上有些特点。
思考:在学习本节课之前,学生认为长方形是“扁扁长长”的,而正方形是“方方正正”的。是什么特征使这两个图形呈现出这样的形态?观察图形特征的角度在哪儿?这些是学生亟待了解的问题。没有参照物,特征就不能凸显。让学生在多种平面图形中将长方形和正方形挑出来,这既符合学生对两种图形的 “直观辨认水平”,也可以帮助学生在图形的对比中主动捕捉观察视角——图形的边和角,并初步尝试描述两种图形的特征。

1.验证。
师:刚才我们讨论了长方形和正方形的特点,可这些特点都是我们看到的、猜测的,怎么验证刚才我们提出的这几个猜想呢?
生:可以用三角尺比一比长方形、正方形上的4个角,看它们是不是直角。
生:可以把长方形和正方形分别对折,看对边是否重合。
生:可以用尺子量一量边的长度,看是否相等。
师:请你们选择自己喜欢的方法,验证一下长方形和正方形的边和角的特点。
(学生验证,教师巡视。然后学生展示汇报)
汇报1:
生:我把三角尺上的直角放在长方形和正方形的4个角上,都能完全重合,证明了长方形和正方形都有4个直角。
汇报2:
生:我手里的长方形上下2条边的长度都是14厘米,左右2条边的长度都是7厘米。长方形的上下2条边一样长,左右2条边一样长。
生:我用的是对折的方法。将长方形上下对折,证明了上下2条边一样长;左右对折,证明了左右2条边一样长。
师:虽然我们手里的长方形大小不一样,但通过验证,都得出了一个结论——长方形的对边相等。
汇报3:
生:我用尺子量了正方形的每一条边,都是12厘米。
生:我用对折的方法证明正方形的4条边都相等。(如图1)我把正方形上下对折,证明了1号边和3号边相等;把正方形左右对折,证明了2号边和4号边相等。

图1
师:这么说,正方形的对边也相等。可我们的猜想是正方形4条边都相等,怎么验证呢?
生:斜着对折正方形,相邻的2条边也完全重合,证明了1号边和2号边相等,3号边和4号边相等。所以,正方形的4条边都相等。
生:我把正方形斜着对折,再对折。正方形的4条边都重合在一起,证明了正方形4条边都相等。
2.比较。
师:刚才我们通过量、折、比等方法,验证了之前关于图形特征的猜想。那么,长方形和正方形有什么相同的地方和不同的地方?
生:它们都有4个直角。长方形是对边相等,而正方形是4条边都相等。
思考:用折、量、比等方法验证长方形、正方形的边和角的特征,既是对前面猜想的证实,更有助于学生在操作验证的过程中深入感受、理解两种图形的特征。这些看似简单的操作体验活动,正是学生走近图形本质特征的过程,是学生积累探究图形特征的学习经验的过程。在操作验证的过程中,培养了学生实践、推理、空间想象等多种能力。

1.学生画图。
师:请同学们在方格纸上画1个长方形和1个正方形。
(展示作品,并引导学生运用特征进行检验)
2.介绍各部分名称。
师:在长方形里,比较长的2两条边叫作长,而比较短的2条边叫作宽。长方形有几条长和几条宽呢?
生:长方形有2条长和2条宽。

1.变一变。
师:看这个长方形,它的长和宽在哪儿呢?(如图2)
图2
生:左右2条边是长,上下2条边是宽。
师:小狗觉得这个长方形太瘦了,想把它变得胖一点。待会儿在小狗拉动图形的过程中,请你们把图形名称说出来,好吗?
(出示课件,如图3)

图3
生:(齐)长方形、长方形、正方形、长方形……
师:小狗拉动图形的过程中,所形成的图形都是长方形吗?
生:不是,还有正方形。
师:什么时候拉成的图形是正方形呢?
生:长和宽相等的时候,所形成的图形就是正方形。
师:为什么它是一个正方形,你是怎么判断的?
生:因为它的4条边都相等,长度都是4格,而且它有4个直角。
师:继续往右拉,所形成的图形都是长方形。还有没有其他办法能把这个图形拉成正方形?
生:可以往上拉。
师:小狗准备把这个长方形的长往上拉。当把它拉成正方形的时候,你们就喊停。
(出示课件,如图4)

图4
生:停!
师:现在这个图形是正方形吗?
生:不是,超过了。现在左右2条边比上下2条边长一些,不是正方形。
师:那该怎么办呢?
生:再往下推一点点。
(出示课件,如图5)

图5
生:停。
师:现在是正方形吗?你还能区分出哪条边长,哪条边短吗?它的4条边还能叫“长”或“宽”吗?
生:不能。
师:正方形的每一条边都相等,都叫作“边”。
思考:在学生的眼里,长方形和正方形是两个截然不同的图形,难以找到它们之间的联系。本环节创设了“小狗拉图形”这种学生喜闻乐见的情境,巧妙地将两种图形的关系隐匿其中。学生在观察图形变化的过程中,能够感受到正方形就 “藏身”在长方形里。
2.找一找。
师:我们和图形宝宝们玩了一节课,它们该回家了。这儿有4个图形,还有2个家。(见图6)家门口的小士兵说了,符合门口上方的2个条件才可以进门。哪些图形可以回家呢?为什么?
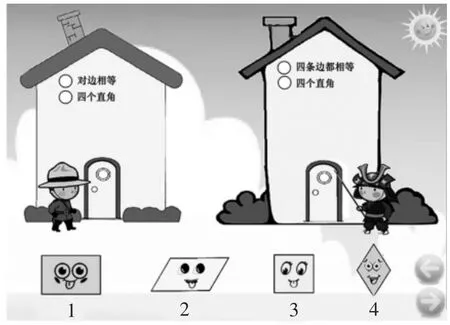
图6
生:1号图形可以回左边的家,3号图形可以回右边的家。
师:2号和4号图形能进这2个家吗?
生:不能进。
师:可是,2号图形想回左边的家。
(播放课件——2号图形画外音:我的对边相等,可以进去吗?)
生:不让进,因为2号图形没有4个直角。
师:4号图形可以回右边的家吗?
(播放课件——4号图形画外音:我的4条边一样长,可以进去吗?)
生:还是不能进,因为4号图形没有4个直角。
师:正方形虽然找到了自己的家,但它挺贪心,说它还有一个家。
(播放课件——3号图形的画外音:左边的家也是我的家,可以进去吗?)
生:能进。
生:不能进。
师:到底能不能进?把你的想法和同桌交流一下。
(学生讨论,然后汇报)
生:正方形不能进左边的家。它虽然有4个直角,但它是4条边都相等,不是对边相等。
生:我觉得正方形可以进左边的家。它的4条边都相等,也是对边相等。
师:你们同意谁的看法?正方形到底能不能进左边的家?(生:能)其他正方形也想住进长方形的家。图形国王就在长方形的家里开了一个小房间,让正方形们都住进去。从此,正方形就住在了长方形的家里。(如图7)
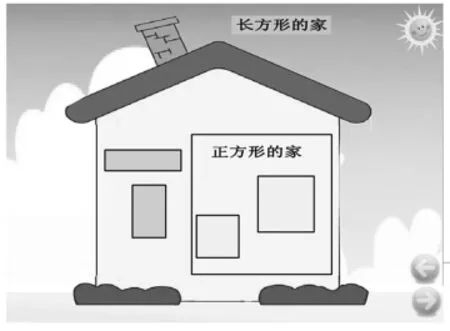
图7
师:正方形住进了长方形的家,长方形也有话说。
(出示课件——1号图形画外音:我能住正方形的房间吗?)
生:不能。因为长方形的对边虽然相等,但它的4条边不一样长,所以不能住进正方形的房间。
思考:如何将正方形与长方形的关系“润物无声”地让学生感知领悟,是我执教时思考的一个问题。利用“图形回家”这样富有童趣的情境来教学不失为一个良策。要让正方形“住进”长方形的家,这是学生认知上的一个“坎”。原以为毫不相干的两种图形要融为一体,对学生来说具有一定的思维难度。学生在思考“正方形是否具备对边相等的特征”的过程中,已经在自我打破原有认知误区,形成新的认知结构。尽管没有直接点出“正方形是特殊的长方形”这一结论,但在学生的脑海里,正方形已经“住进了长方形的家”,这一步对学生而言弥足珍贵,是对长方形、正方形认识的一次升华,是对两种图形特征认识的进一步完善。

师:同学们,今天我们认识了哪两种图形?(生答略)我们是用哪些方法探究出这些图形的特点的?
生:用尺子量出长方形、正方形边的长度,验证了这两种图形边的特点。
生:用对折的方法,验证了长方形对边相等、正方形4条边都相等的特点。
生:用三角尺上的直角去比一比,验证了两种图形的4个角都是直角。
师:量、折、比都是我们探究图形特征的好方法。将来,我们还将用这些方法探究更加丰富的图形世界。
(作者单位:福建厦门实验小学集美分校)

