美国加州教材立体图形部分的编排特点与启示
◇施银燕
美国加州教材立体图形部分的编排特点与启示
◇施银燕
与我国各个版本小学数学教材相同的是,美国加州教材中立体图形的认识也分两个阶段:第一阶段是感性认识,从整体上把握立体图形的特点;第二阶段则是理性认识,从面、棱、顶点几个要素进行细致的分析,并进一步研究这些立体图形的表面积和体积。但是,深入到具体内容的编排以及同一内容的教学方式上,还是能看到与我国教材的差异。从这些差异的背后,能看到两国数学教学的不同追求。下面对美国加州教材(以McGraw-Hill公司出版的 California Mathematics)第二阶段立体图形的内容、结构、具体教学方式进行分析,以期能对我们的教学有所启发。
一 立体图形的认识:内容呈现系统化、结构化
我国教材中对立体图形的认识(仅指第二学段)分两次进行:五年级认识长方体、正方体;六年级认识圆柱和圆锥。到总复习时才对立体图形进行整体上的梳理和概括。
而美国教材则将所有立体图形的认识安排在一个单元完成。首先定义三维图形,即有长、宽和高这三个维度的图形。随后,介绍三维图形中常用的概念:面、侧面、底面、棱、顶点。(见下图)
许多常见物体的形状是三维的,也就是说,它们有长、宽和深(或高)这三个维度。下面是三维图形里常用的一些术语。

随后,根据图形是否含有曲面,把图形分成了两类:一类是棱柱和棱锥(不含曲面),另一类是圆柱、圆锥和球(含曲面)。
在介绍棱柱特点时,引进了“全等”这一概念。研究棱柱和棱锥特点时,还给出了棱柱和棱锥的命名规则,即以底面形状而得名。如底面是长方形的棱柱,称为“长方柱”;底面是正方形的棱锥,称为“正方锥”。介绍了棱柱和棱锥的一般特点和命名规则后,教材中也会出现一些新的棱锥,如五棱锥、八棱锥等立体图形让学生来辨认。如:
对于下面每个图形,先指出底面的形状,再分类。

无论是哪种立体图形,描述其特征都离不开前面的那些概念:面、侧面、底面、棱、顶点等。
显然,美国教材中涉及的立体图形比我国的要多。曾经有人用“一英里宽一英寸深”来形容美国教材宽而浅的特点。从这部分内容来看,我们明显感受到了“宽”,认识的立体图形更多、更丰富。但是,这个“宽”,在我看来并不导致浅,反而因为“宽”,知识的呈现方式由零散变得有组织,显得更有结构、更清晰(如下表)。结构化的呈现方式会让学习负担更轻,更有利于学生“把书读薄”。

三维图形(有三个维度)柱(有两个全等的底面) 锥(有一个底面)不含曲面含有曲面棱柱(侧面为平行四边形)圆柱(底面为全等的圆,侧面为曲面)棱锥(侧面为三角形)圆锥(底面为圆,侧面为曲面)
因为认识了各种棱柱和棱锥,更便于学生概括出有序计数面、棱、顶点的方法,更容易发现这些数量之间存在的一般规律。例如:底面是n边形的棱柱,面、棱、顶点分别有 n+2、3n、2n 个。学生很容易看出:面数+顶点数-棱数=2。再由这一类图形推广到棱锥,甚至其他更为一般的图形。
二 体积与表面积:内容有增有减,强调基本方法
内容上,体积限于棱柱(包括长方体和三棱柱)和圆柱,棱锥和圆锥则不涉及;表面积限于棱柱、棱锥、圆柱,不涉及圆锥。和我国的教材相比,增加了三棱柱的体积,但减少了圆锥的体积;增加了三棱柱、棱锥的表面积。
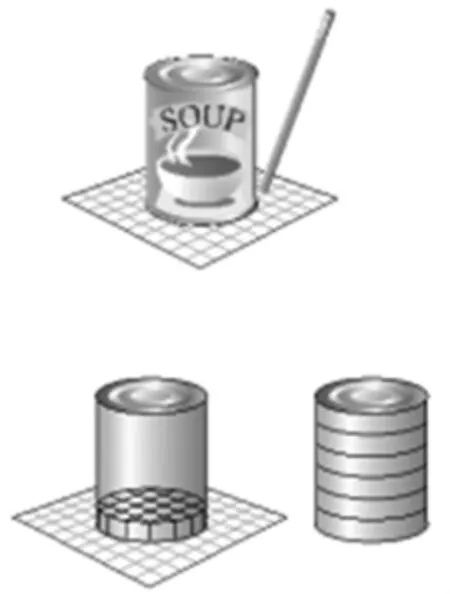
从教材图中我们可以发现,增加三棱柱体积后,从长方体到三棱柱,再到圆柱,强调的是体积概念的共性、柱体求体积方法的共性,即始终强调:体积就是物体包含的单位立方体的个数;对柱体而言,底面积对应着一层摆放单位立方体的个数,高对应摆放的层数。(如下图)

三棱柱的底面为三角形,下图表明,三棱柱的体积也是底面积B与高H的乘积。

把一个圆柱形的罐头放在方格纸上,仿照右图,把底面描下来。
1.估计底层摆放的小立方体个数(不是整个的小立方体也要考虑)。
2.如果每层都是1cm高,这个圆柱里能摆多少层。
3.猜想:这个圆柱形罐头的体积是多少?
对比我国的教材:长方体体积公式是用摆单位立方体来探索的;圆柱的体积公式,则是把圆柱沿着底面直径切开转化成长方体得出的;圆锥的体积公式,是通过倒水或倒沙等实验,依据等底等高圆柱和圆锥体积的关系得到的。求三种图形的体积,便是三种方法。
我国的教材里始终强调的是更为上位的 “转化”思想。但即使学生有转化的需求,因为一图一法,如何实现转化还是有相当大的难度的;相比较而言,美国教材强调的更为基本,学生也更容易迁移。
美国教材中没有编排圆锥的体积,这一点同样值得我们思考。在小学阶段,圆锥的体积公式只能依赖猜测、实验、观察得出结论,对学生“为什么”的追问,老师很难解释。现在想来,教材中不编排圆锥的体积计算自有它的好处。只是通过倒水得到的结论,叫作猜测可能更为合适。既然如此,何必作为一个既定结论让学生反复记忆训练呢?如果可能的话,我建议圆锥体积可以作为圆柱体积之后的一节开放性的探索课,但对于结论和结论的应用可不作要求。
教材的一加一减,可以看出其背后不同的价值取向。我们强调应用、解决实际问题(实际生活中有大量需要计算圆锥体积的问题),而美国教材更强调其背后的基本原理。
美国教材中,表面积的内容则分两次进行编排。第一次是结合组合图形面积的教学,进行展开图与表面积的探索,包括三棱柱、三棱锥、四棱锥等的表面积,但并没有总结出计算公式,又一次体现了“广”的特点。第二次,则是在学习了勾股定理之后,有一些数据需要根据勾股定理来求出。在这个阶段,还总结出了长方体和圆柱的表面积计算公式。我认为,结合展开图进行各种立体图形表面积的探索是比较好的,但给出公式似乎没有必要。
三 淡化计算,强化推理
美国教材中包含不少需要推理的问题,如:
【挑战】两张同样的长方形纸,分别沿着长和宽卷成圆柱。哪个圆柱的体积更大?解释你的结论。

【开放式问题】画一个圆柱,要求:底面半径比右面圆柱的更大,而体积却更小,并标上数据。

这些问题不提供数据,答案不唯一,过程方法更为多样,能让不同层次的学生参与探索,强调每个学生用自己的已有知识去讲道理。
与重视推理相对的是,教材对计算有所淡化。几乎所有求圆柱表面积和体积的问题,都不要求算出准确结果,只要求结果保留一位小数;或者改变问题呈现方式,从而通过估计或者推理就能得出结论。如:
求圆柱的体积,结果保留一位小数。
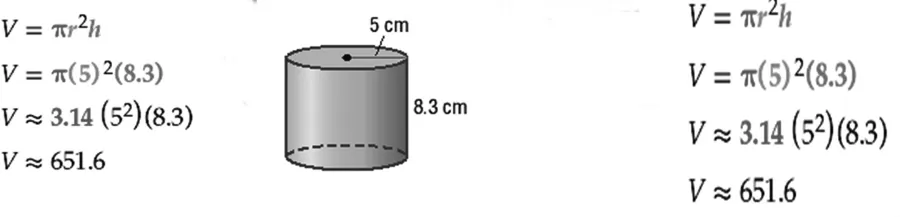
V=πr2h
V=π×(5)2×(8.3)
V≈3.14×(5)2×(8.3)
V≈651.6
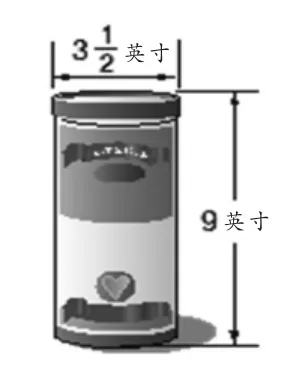
哪个选项最接近这个麦片桶的容积(单位:立方英寸)?
A.32 B.42.78 C.75.92 D.86.55
熟悉小学高年级数学的老师都有这样的感受,那就是“圆柱与圆锥”这一单元,学生对相应的概念、公式、方法都已经掌握,却总在计算上出错。新课程改革之后,对整数、小数计算的要求已经降低,但到学习圆柱、圆锥这部分内容时,计算难度并没有降下来。圆柱、圆锥的教学中,如果我们能让学生从计算中解放出来,学生的空间想象能力、推理能力等目标就能更好地得到落实。
(作者单位:北京第二实验小学)

