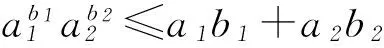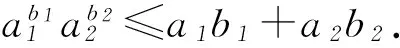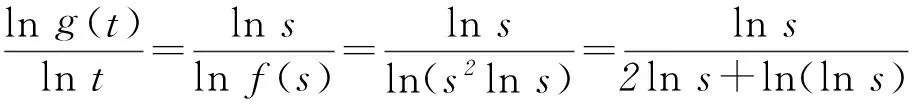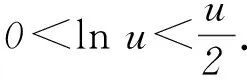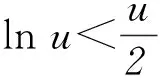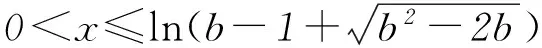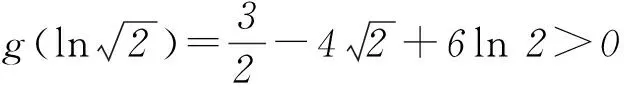立足结论，突破障碍

◇　四川　李菁菁　高　明



立足结论，突破障碍

◇四川李菁菁高明

函数问题常作为高考的压轴题,这类题目通常含有两三个小问,大多数考生只会做第(1)问,对于剩下的问题,或是思维受阻,或是时间不足,未能有效地解决问题．实际上,有些函数压轴题并没有想象中那么困难,解题的关键是立足结论,寻找突破思维障碍的途径与方法．本文以高考试题为例阐述立足结论、突破障碍的解题方法．

1比对结论,寻找解题切入契机

这里的结论不仅包含问题本身的结论,还包含已求解得到的结论．解题时要善于抓住结论的结构特征,通过类比、对比的方式比对结论相似之处,寻找解题的切入点与契合点．

(1) 求f(x)的最小值;

(2) 试用(1)的结果证明如下命题:

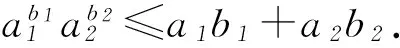
实际上,当a1、a2中至少有1个为0时,不等式显然成立.

当a1、a2均不为0时,此时将已知结论与未知结论联系起来,发现:由(1)的结论“当0

由于b1>0,b2>0且b1+b2=1,故

0

比对r+(1-r)=1与b1+b2=1以及

看b1与b2分别与r、1-r相对应,有

xb1≤b1x+(1-b1)．

即

2转化结论,实现命题等价变换

变换题目要证明的结论,将陌生的、复杂的结论转换为熟悉的、简单的、易于解答的结论,实现结论等价转换,化难为易,优化解题过程．

(1) 求函数f(x)的单调区间;

(2) 证明:对任意的t>0,存在唯一的s,使t=f(s);

第(3)问许多考生却解答不出,究其原因是未能很好地理解题意、转化问题结论的形式．

事实上,可先从第(3)问的结论出发,即

3挖掘结论,构建解题递进桥梁

挖掘题目结论中的隐含信息,使隐含信息外显化,从而与已知结论联系起来,构建解题桥梁．

(1) 讨论f(x)的单调性;

(2) 设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值;

(2) 对g(x)求导可得

g′(x)=2(ex+e-x-2)(ex+e-x-2b+2)．

当b≤2时,g′(x)≥0,即g(x)在R上单调递增,因为g(0)=0,故∀x>0,g(x)>0．而当b>2时,

2

(作者单位：西华师范大学数学与信息学院)