初中数学教学中规律探索题的研究

□ 上海市新泾中学 林开全



初中数学教学中规律探索题的研究

□ 上海市新泾中学 林开全

一、数字变化规律探索型

数字变化规律探索问题是最常见的规律探索题。此类问题探索一般的方法是：认真观察这些数字相邻的两数有什么数量关系，再猜想、归纳一般规律，最后用实例加以验证.最终解决问题。

例1：观察右图中一列有规律的数，然后在“？”处填上一个合适的数，这个数是____。

问：先从相邻的两数有什么规律思考，学生容易想到后面的一个数与前面的一个数的差依次是3，5，7，9，11，13……所以48后面的数应该是48+15=63。故应填上63。对于这种方法再说明其有局限性，它只是适用于项数不多时，不是作为求任意第n个数的通用方法，再让学生思考别的方法。

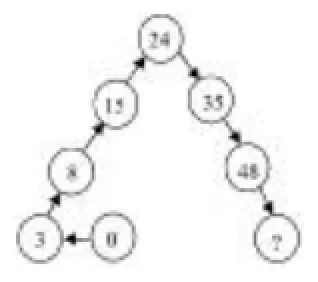
经过思考，部分学生能探索到规律：因为0=12-1，3= 22-1，8=32-1，15=42-1，24=52-1，35=62-1，48=72-1……所以第n个数是n2-1，即48后面的一个数应是82-1=63，故应填上63。也就是说0，3，8，15，24，35，48……都是比相应的平方数小1。这种方法具有一般性，可以求任意第n个数。

通过本题可以让学生得到数字类规律题的探索方法，即考虑相邻两数的差（或倍数）的关系，常见的情况有：前后相邻两数的差相等，前后相邻两数的商相等，或是相邻两数的和（或积）与后一个数的关系。但是思维不能定势，要从多方面去考虑问题。

二、数学运算规律探索型

这类问题一般是给出一组算式，引导学生细心观察算式的特征，努力发现其中的规律，明确各知识点的联系，提出数学模型的猜想，得出一般的结论，再利用实例进行验证猜想规律的正误。这一探索规律的过程中，提高了学生参与教学活动的积极性，激发学生的主动学习的欲望，使他们亲自经历探索过程与思维升华的过程，从而培养了学生观察、实验、推理的能力及创新意识。

（1）你发现了什么？它的第n个数是_______。

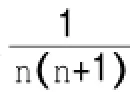
三、图形变化规律探索型

这类问题一般是呈现一组有规律的图形,让学生观察图形的结构及其变化情况,猜想、探索或归纳出图形的变化规律，再由前面的实例进行验证，并根据这个规律解决问题。这样有利于学生主体意识和主体能力的形成和发展，培养了学生的实践能力。

解决这类问题要注意将数形结合起来，数形结合思想是规律探索题常用的思想方法。本题的教学就有效地提高了学生观察、猜想、验证、推断等各种能力。对规律题的探索就是让学生在体验数学活动充满着探索与创造的过程中发展自己的实践能力和创新能力。

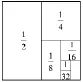
图1

四、循环排列规律探索型

这类问题一般是数字或图形有序循环排列起来。解题时应让学生细心观察其数字或图形变化隐含的规律，一般情况下其相邻两数或两图形无规律可找，而是由某些数字或某些图形循环出现的。这类问题要注意结合数字或图形的特点，抓住事物不变的本质，运用类比、归纳、数形结合、猜想等思想方法探索出规律。这类题型也体现了课程标准中的“学生的数学学习内容应当是现实、有意义的、富有挑战性的……”的理念。

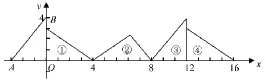
图2

这类题目是填空题难度比较大的题目，的确有很大一部分学生不会做这题，甚至有个别学生实在做不出就一个图形一个图形地画过去。当然三角形⑩是可以画出来的，但是如果把题目改求第100个三角形,求第n个三角呢？还能画得出来吗？回答是否定的。因为这样没有掌握事物的本质属性——图形的变化规律。

那如何去引导学生探索此题的规律呢？让学生来一起仔细地观察一下题中条件和图形，三角形的旋转变换过程中图形的摆放位置有什么规律？在教师的引导下，经观察思考，学生能发现在图④的摆放方式和图①的一样，因此可猜测这些图形是每三个图形一次循环，它在x轴上距离是12个单位长度。因为10除以3得3余1，故图⑩的摆放方式同图①，那么题中要求的坐标就是（36，0）。其他情况以此类推。

本题是一道循环运动图形的操作规律探索题，在观察、操作、归纳的基础上探索出循环规律，使感性认识上升到理性认识。此题的教学有效地提高了学生的探索能力、空间思维能力和综合能力。