基于EWT和多尺度熵的轴承特征提取及分类
李沁雪,廖晓文,张清华 ,崔得龙
(1.广东石油化工学院 计算机与电子信息学院,广东 茂名 525000;2.广东省石化装备故障诊断重点 实验室,广东 茂名 525000;3.华南理工大学 自动化科学与工程学院,广州 510640)
轴承故障诊断的关键是从振动信号中提取出有意义的故障特征信息,特征提取直接决定了后期故障诊断的正确性。随着非线性科学理论的发展,小波分解、EMD[1]、样本熵等众多非线性方法和参数被广泛应用于机械设备故障诊断领域。具有良好自适应性的EEMD[2]利用白噪声改善了EMD的模态混叠,在众多的特征提取方法中脱颖而出。然而,EEMD和EMD均属于类小波结构的递归筛分算法,缺乏完备的数学理论,分解模态较多,且每个模态的提取需要多次迭代,其中EEMD还需对分解的IMF求总体平均,需进行多次EMD,分解计算量较大。
针对EEMD及EMD的不足,文献[3]在小波理论的框架下,结合EMD的自适应性,提出了经验小波变换(Empirical Wavelet Transform,EWT)。EWT是一种自适应信号处理方法,由于其根据小波的构造方式构造经验小波,理论依据完备且计算量远小于EEMD和EMD。
在此,将EWT与多尺度熵相结合,用于轴承振动信号的前期信息提取和故障分类,并利用其对信号复杂程度的良好分类特性,提出了一种基于经验小波和多尺度熵的轴承故障诊断方法。
1 经验小波变换
EWT是在EMD的基础上,结合小波变换理论提出的一种具有自适应性的特征提取方法,其本质是根据信号的频谱特性对信号频谱进行自适应地分割,以构建一系列带宽适合的带通滤波器,从而提取具有紧支撑频谱特性的调频调幅模态。
1.1 关键环节
1.1.1 Fourier支撑的分割
假设在频域内将[0,π]分割为N个连续的片段Λn=[ωn-1,ωn];n=1,2,…,N。其中ωn为各段的边界,其值选择为信号Fourier谱相邻2个最大值之间的极小值,但ω0=0且ωn=π。如图1所示,图中阴影区表示了以ωn为中心,宽度Tn=2τn的过渡段。
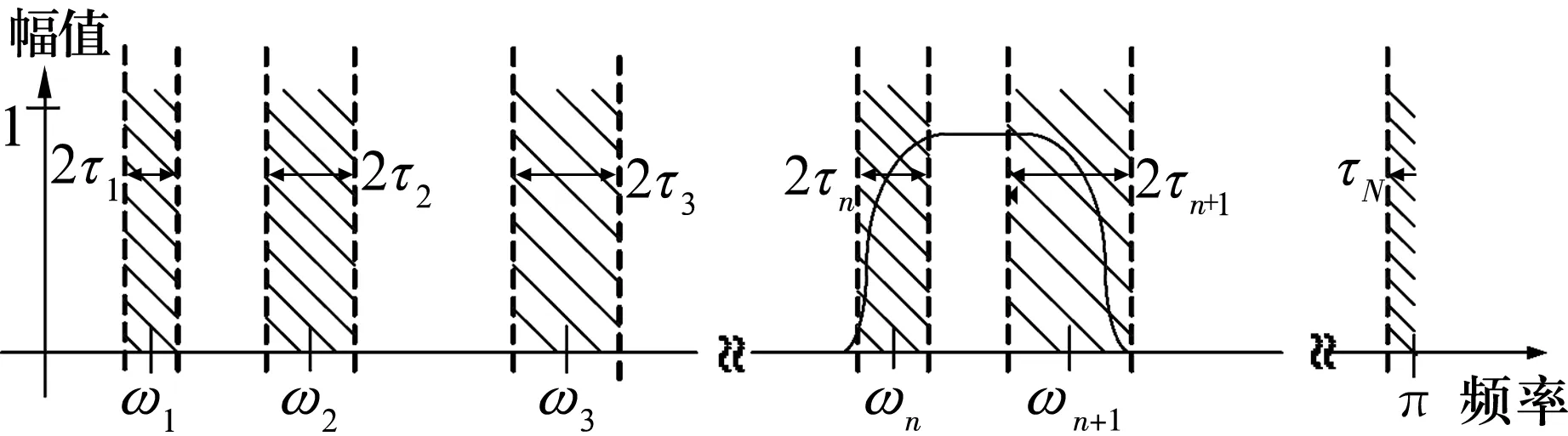
图1 Fourier坐标轴的分割
Fourier分割的关键是确定边界ωn,即确定N。文献[3]采用了一种易于理解的阈值法,计算频域内m个幅值极大值Mi(i=1,2,…,m),按递减的顺序排列,令M1≥M2≥…≥Mm并归一化到[0,1]。规定所有的Mi均需大于阈值Mm+α(M1-Mm),其中α∈(0,1),为相对振幅比。当α确定后,则N为大于阈值的最大值点的个数。因此,可取大于阈值的前N个最大值所对应的ωn为N-1个边界。
1.1.2 核心函数的定义
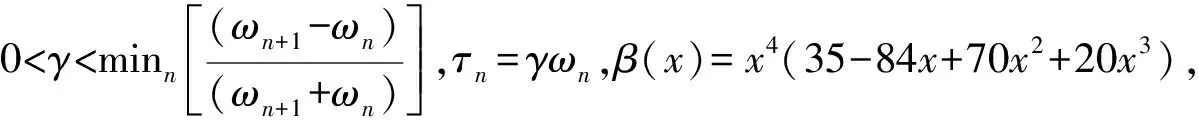
。(1)

。(2)
1.1.3 信号重构及经验模态的生成
原始信号的重构公式定义为
(3)
则经验模态各分量fk(t)为
f0(t)=Wf(0,t)*φ1(t),
(4)
fk(t)=Wf(k,t)*ψk(t)。
(5)
1.2 最优模态的选择
振动信号进行EWT后,可通过对无关模态的剔除或最优模态的选择达到去除干扰信息的目的,更加准确地提取出轴承的有效故障信息。文献[5]推导得出:EMD各模态与原信号的相关性约等于各分量的自相关。因此借鉴该方法,将EWT后各模态与原信号的相关系数作为评定各模态分量可靠性的指标。其定义为
,(6)
式中:fk(t),f(t)分别为EWT后的各模态分量和原始信号;μfk,σfk,μf,σf分别为fk(t)和f(t)对应的时域均值和标准差;E为数学期望。ρf,fk反映了fk(t)分量与原始信号在时域中的相关性,其数值越大,表明fk(t)分量与原始信号越相关,即自相关性越大,说明周期性的故障冲击成分比例越高。因此,选择相关性最大的模态作为EWT的最优模态,并将其作为下一步故障分类和识别的分析样本。
2 基于多尺度熵的故障分类
样本熵只能反映时间序列在单一尺度上的复杂度,因此,为反映时间序列在不同尺度因子下的自相似性,文献[6]在样本熵的基础上提出了衡量时间序列在多尺度下的复杂度和无规则程度的方法——多尺度熵[7-8](Multi-Scale Entropy,MSE)。对于滚动轴承而言,故障信息越多,熵值将越小,也意味着故障信号的复杂度降低,序列的自相似性越高。多尺度熵即在原始信号的多个尺度上计算样本熵,计算方法如下:
1)假设原始序列为Xi={x1,x2,…,xN},通过人为给定的嵌入维数m和相似容限r,尺度因子η取正整数,建立新的粗粒向量为

2)求取每一个粗粒序列的样本熵,得到η个样本熵值,将多尺度熵绘制成以尺度因子η为自变量的函数,进行多尺度熵分析。在此,多尺度熵参数设置为:m=20,r=0.15。需要指出的是,若时间序列a在大部分尺度上都比另一个序列b的熵值大,则可认为b具有更低的复杂性和更高的自相似性,并包含更多的故障信息。
3 故障特征提取流程
1)采集多种轴承状态振动信号,并分别进行频域上的自适应分割。
2)选择一组经验小波滤波器组,提取同一信号的不同AM-FM模态。
3)计算同一信号各模态分量与原信号的相关系数。
4)取相关系数值最大模态为同一信号最优模态。
5)计算多种轴承状态振动信号最优模态在多个尺度上的样本熵,即多尺度熵。
6)根据不同轴承状态的多尺度熵进行轴承状态分类。
7)将不同轴承状态的多尺度熵作为神经网络或支持向量机的输入特征向量,判断故障类型。
4 试验分析
试验轴承的振动加速度数据来自于Case Western Reserve University[9]电气工程实验室。试验装置由感应电动机、扭矩传感器/记录仪、测力计等组成,振动加速度传感器分别安装在电机壳体的驱动端和风扇端,电动机转速为1 750 r/min,采样频率为12 kHz。试验轴承为SKF6205-2RS深沟球轴承,轴承主要参数见表1。轴承损伤为单一损伤,由电火花机分别在轴承内圈、外圈及钢球上加工,其中外圈、钢球故障直径均为0.177 8 mm,内圈故障直径分别取0.177 8 mm(内圈故障1),0.355 6 mm(内圈故障2)和0.533 4 mm(内圈故障3)。

表1 轴承主要参数
4.1 故障特征提取
分别对外圈故障、内圈故障1和钢球故障轴承的实测信号进行处理,3种状态下故障信号的EWT最优模态的包络谱分析结果如图2所示。
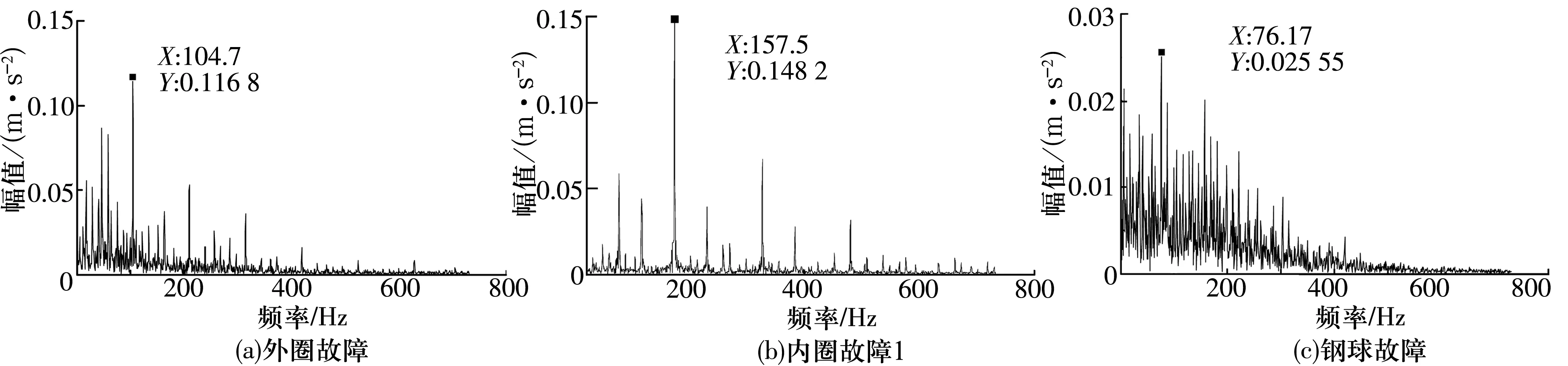
图2 不同故障信号EWT最优模态包络谱
根据表1中参数计算可得[9],外圈故障、内圈故障1、钢球故障的特征频率分别为104.6,157.9,69 Hz。从图中可以看出,EWT顺利地提取出了轴承外圈及内圈故障1的故障特征频率,而钢球故障频率与理论值相差约8 Hz,原因可能是钢球故障较难通过振动信号明显传递,是相对较难提取的故障类型,但从3种故障类型的理论故障频率的差值来看,从图2c中也不难判断是钢球故障。判断结果说明,EWT是一种有效的轴承故障信息提取算法,故障频率区分度高,轴承内、外圈故障信息提取非常准确,可为下一步故障分类提供可靠的故障信息。
4.2 多尺度熵分类
MSE可作为判断指标和特征参数,用以表征不同故障类型或状态轴承振动信号在不同η时的复杂性或无序性。取η=20,计算20个粗粒向量的样本熵,得到6种状态下的分类结果如图3所示。
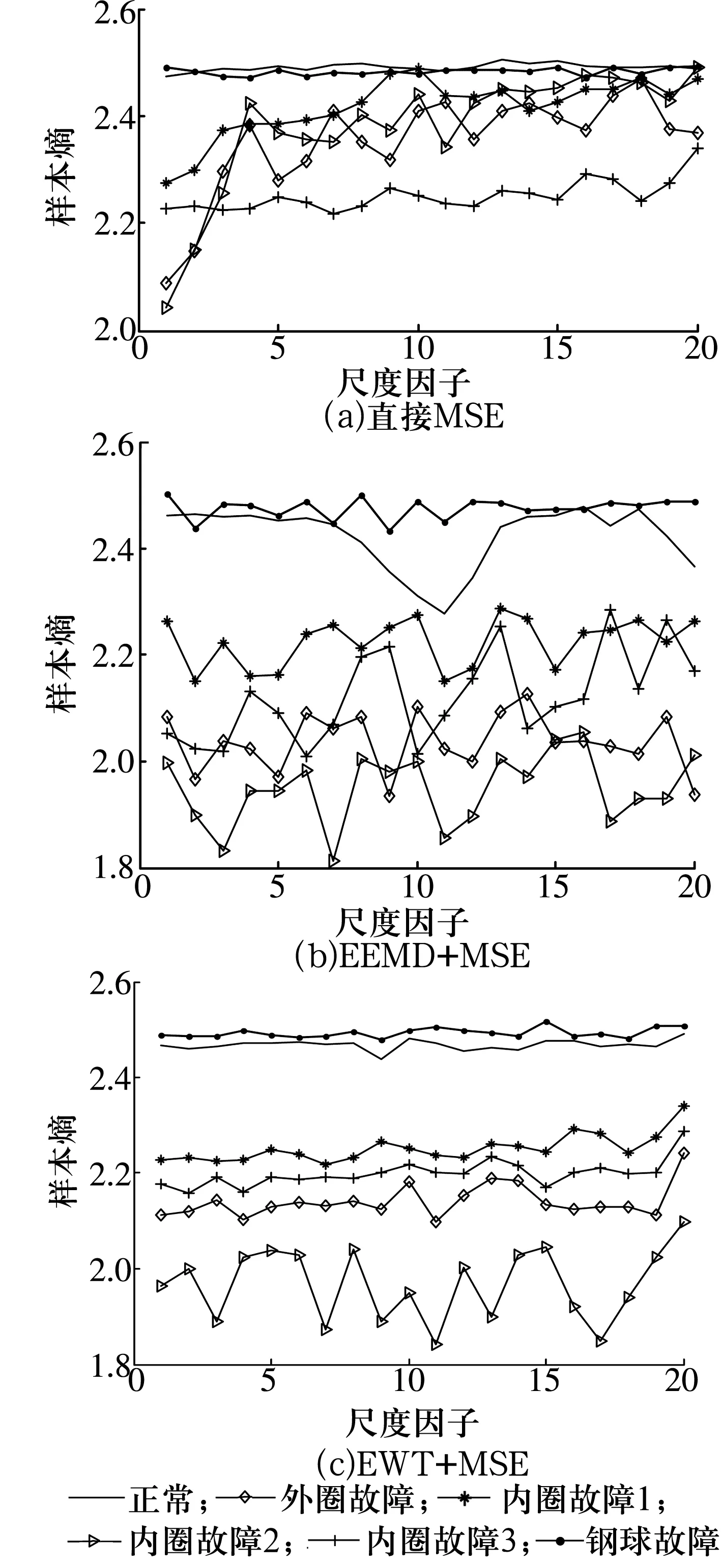
图3 轴承不同故障状态的分类结果
对比可知:直接进行MSE时,6种状态在多数尺度上几乎无法分类;EEMD+MSE的故障分类效果虽有较大改善,但钢球故障与轴承正常状态之间、内圈与外圈故障之间也基本无法区分;而6种状态信号经过EWT得到的最优模态在20个尺度上的样本熵基本均处于不同的数值区间,分类效果明显优于其他2种方法。
从图3c可以看出: 正常及钢球故障的熵值相对较高,说明对应振动信号的复杂度高;内圈和外圈故障信号的熵值较低,说明这2种故障的故障冲击规律性强,更有序且复杂度更低;除了外圈故障与内圈故障3在个别η数值点样本熵略微接近外,本文所提方法总体分类效果很好,尤其当η处于4~9,11和15~19数值区间或数值点时,分类效果更好,因此尺度因子的合理选择对于故障分类也起到关键作用。
5 结束语
提出了基于经验小波变换和多尺度熵、具有自适应性的轴承故障信息提取和分类方法,其能够体现出EWT优秀的模态分解和特征提取能力,可以较好地区分轴承不同故障状态(包含多种故障和同一故障下不同故障程度),故障分类效果在尺度因子选择合理的前提下具有明显的优势,故障类间无重叠,是一种有效的自适应故障信息提取和分类方法。
但是,经验小波变换的研究尚处于起步阶段,未来还可开发出更好的频谱分割方式,也可引入小波包理论等其他方法替代小波变换,而且还可以考虑采用新的聚类方式确定分解模态数,提高其自适应性。

