基于弹塑性有限元方法的转盘轴承材料许用接触应力研究
郑红梅,田贵,梁昌文,郑岩,李庚袁
(合肥工业大学 机械与汽车工程学院,合肥 230009)
转盘轴承承受的工作载荷大而接触面小,应力集中明显,滚道的损坏是其主要失效形式,因此材料应具有良好的力学性能[1-2]和较高的耐磨性[3],且能承受较高的接触应力。对于转盘球轴承,工作中沟道可承受高达4 000 MPa以上的交变接触应力。GB/T 4662—2012《滚动轴承 额定静载荷》规定了优质淬硬钢球轴承的许用接触应力为4 200 MPa,其相关参数是基于Hertz理论点接触公式计算的。对于套圈材料为42CrMo和50Mn的非淬透性钢制大型转盘轴承,还没有规定其最大接触应力,因此有必要对其许用接触应力进行测定。文献[4-5]进行了转盘轴承许用接触应力的试验研究,根据试验所获数据,通过Hertz理论计算得到接触应力,对接触应力和对应的压坑深度采用回归分析,测得材料的许用接触应力。
决定转盘轴承材料性能的关键是热处理工艺[6],加工时要对工艺准确把握。许用接触应力测定试验的关键是压痕深度的测量,由于转盘轴承材料良好的力学性能,压痕一般较小,测量需要借助高精度仪器。
以转盘轴承材料50Mn为研究对象,对其进行平板与钢球对压研究,从弹塑性有限元角度分析得到压痕深度,结合文献[4-5]处理接触应力和压痕深度方法,对弹塑性有限元分析的数据进行处理,代替试验测得材料的许用接触应力。
1 弹塑性有限元法
许用接触应力测定试验主要测定卸载后永久压痕深度,利用弹塑性有限元方法得到简化模型,通过分析模型得到试验对应的数据。
转盘轴承材料表面经过感应淬火,表层会出现明显的硬化,压缩屈服强度大大提高,在建立弹塑性有限元模型时需要考虑滚道材料的塑性[7]。为了获得塑性数据,根据GB/T 7314—2005《金属材料 室温压缩试验方法》进行了材料的室温压缩试验,得到表面硬度为57 HRC的转盘轴承材料50Mn的塑性数据,即应力应变关系,见表1。

表1 50Mn材料塑性数据
1.1 弹塑性有限元模型
以平板试样与钢球对压为原型,考虑到模型的对称性,建立1/4模型,如图1所示。基于六面体单元的计算精度和网格数量优于四面体单元[8],全部采用六面体网格,在接触处局部细化网格并加载。

图1 滚球压平板边界条件与载荷加载示意图
网格模型单元数为60 338,节点数为65 133。钢球半径为10 mm,50Mn材料的弹性模量为2.1×105MPa,泊松比为0.3。
1.2 弹塑性有限元分析得到压痕深度
采用ABAQUS软件分析,定义材料属性时将表1数据写入塑性中,分析时弹性和塑性因素全部考虑。施加载荷,卸载后的等效应力分布如图2所示,塑性变形如图3所示,最大Hertz接触应力和压痕深度见表2。由图可知,最大位移出现在钢球和平板接触中心处,应力分布和压痕的形状都与实际相符,可以准确读出压痕深度。

图2 等效应力云图

图3 等效塑性应变图
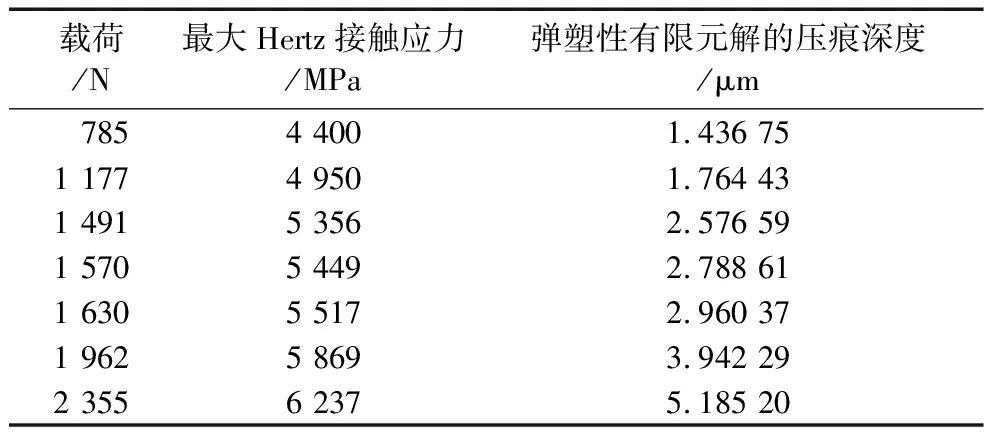
表2 不同载荷下的最大接触应力和压痕深度
2 试验法测量压痕深度
使用中频淬火加工试样(200 mm×50 mm×60 mm),保证与室温压缩试验试样的力学性能相同(表面硬度57 HRC)。
利用电子万能材料试验机(WDW-100)对试样进行多次缓慢加载,加载范围500~5 000 N,达到一定载荷稳定一段时间后卸载,试验装置如图4所示,压头夹持装置上GCr15钢球的直径为10 mm。

1—压力机上砧座;2—垫块;3—压头;4—平板试样;5—压力机下砧座
用轮廓仪测量不同载荷下试样表面冠状压痕深度,部分结果见表3。
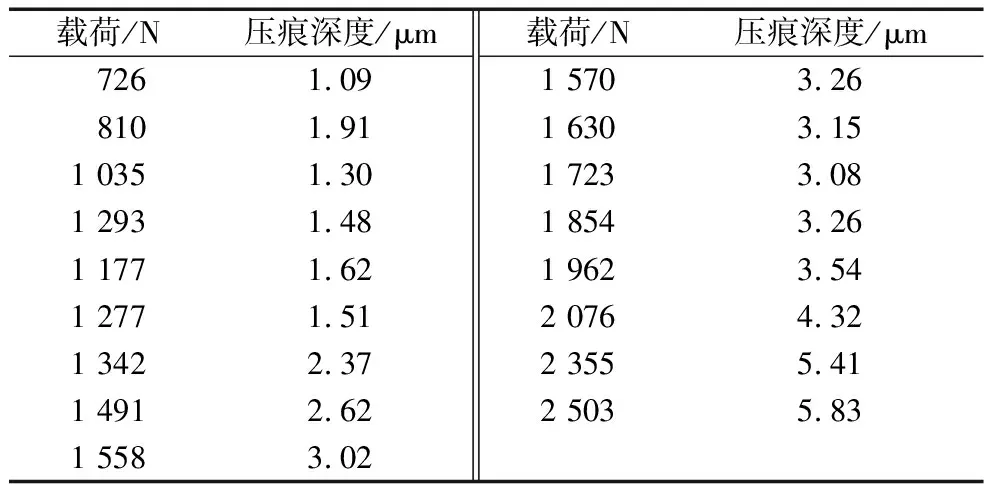
表3 试验数据
3 对比分析
3.1 数据处理
3.1.1 弹塑性有限元方法数据
根据Hertz理论,球与平板对压的最大接触应力为[6]
(1)
式中:P为载荷;E为材料弹性模量;ν为材料泊松比;∑ρ为综合曲率,∑ρ=0.4;μ,w为应力分布系数,球与平板接触情况下μ=w=1。
许用接触应力测定试验采用线性回归法分析接触应力和压痕深度。压痕深度δq与钢球直径Dw之比δq/Dw和最大接触应力σmax的关系为[4-5]
(2)
式中:K为常数;b为指数。

y=a+bx,
(3)
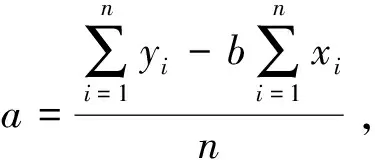
相关系数r为
(4)
将表2的接触应力和压痕深度代入上述公式,即采用回归分析法可得到:a=-17.532 30,b=3.758 226,r=0.942 284。
还原方程得到接触永久变形与钢球直径之比对接触应力的关系方程为
(5)
由于在试验中很难找到准确的弹性变形到塑性变形的临界点,工程上一般以产生0.03%(或0.01%,0.05%)残余变形的应力作为弹性极限[6]。文献[9]认为当转盘轴承滚道的永久变形量为滚子直径的0.03%时,不会影响转盘轴承运转的平稳性和寿命。因此设定沟道塑性变量为钢球直径0.03%时的应力为材料的许用接触应力,故将δq/Dw=0.03%代入(5)式,求得许用接触应力为5 342 MPa。
3.1.2 试验数据
同样用回归分析法处理试验数据,用MATLAB软件进行拟合,拟合曲线如图5所示。
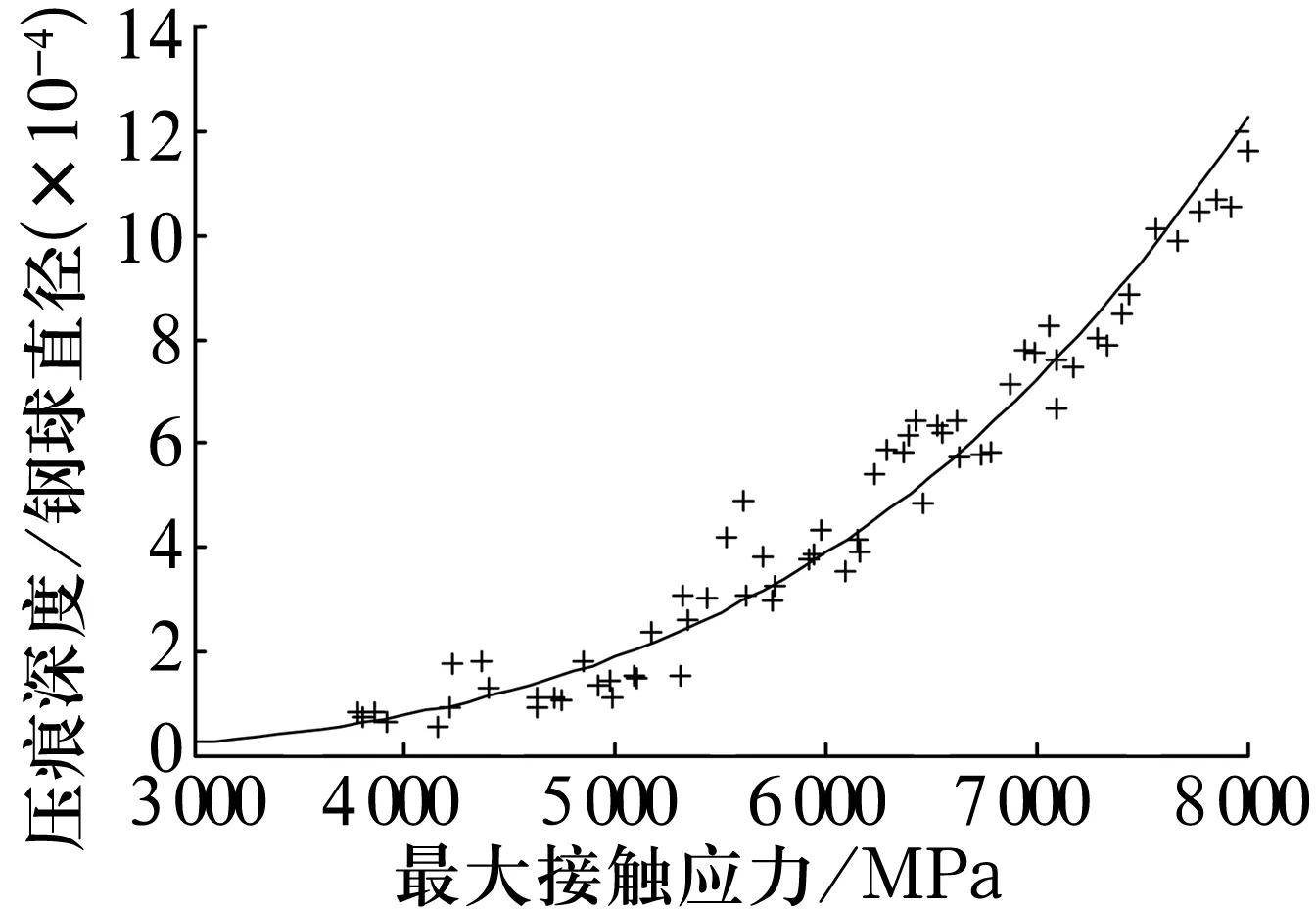
图5 试验数据拟合曲线
根据拟合结果,求得相关系数r=0.964 514,说明σmax与δq/Dw相关。拟合曲线方程为
(6)
由上式求得许用接触应力为5 517 MPa,即永久变形量为钢球直径0.03%时的接触应力,对应的加载载荷为1 630 N。
3.2 结果对比
试验得到的许用接触应力和弹塑性有限元模型分析得到的许用接触应力分别为5 517 MPa和5 342 MPa,误差为3.2%,在工程上是可行的。由于弹塑性有限元计算需要大量时间,文中只计算了部分数据,当弹塑性有限元方法分析的数据更多时误差会更小。将试验的压痕深度和弹塑性有限元分析所得深度进行比较,结果见表4,两者所得结果相近,除个别明显不合理的试验数据,大部分误差在0.05%左右。若塑性特性曲线更加精确,误差会更小。因此,建立的弹塑性有限元模型可以用来测定转盘轴承材料的许用接触应力。
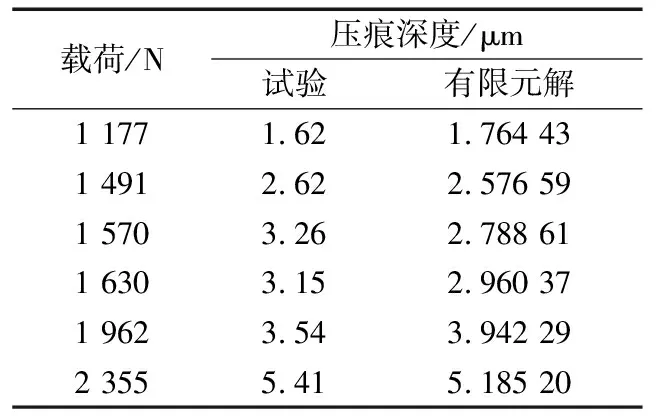
表4 压痕深度对比
4 结束语
建立了50Mn转盘轴承材料接触永久变形与钢球直径之比对接触应力的关系方程,测得了当δq/Dw=0.03%时,转盘轴承材料50Mn与钢球对压试验的许用接触应力值,提出了许用接触应力测定的弹塑性有限元方法,经试验对比证明,该方法可以替代试验法用于测定转盘轴承材料的许用接触应力。

