论数学图型在康德认识论中的示范作用

车 辕

（清华大学马克思主义学院，北京 100084）



论数学图型在康德认识论中的示范作用

车 辕

（清华大学马克思主义学院，北京 100084）

摘 要：康德哲学一方面要捍卫理性的普遍必然性，另一方面也要保证理性能够落实到经验直观之中去。为了在抽象的前者同具体的后者之间搭建起沟通的桥梁，康德提出了图型理论作为概念与直观的中介。而在图型中，数学图形又成为先验图型与经验图型之间的中介。通过这种方式，康德构建起一个逐步由抽象到具体的认知环节。数学图型也显示出人的认知的空间化和可视化的倾向，并且被现代科学实验所证明。因此，研究康德的数学图型，对于其整个认识论的把握起着关键作用，同时也有助于了解人们自身的认知活动。

关键词：数学图型；想象力；认识论；空间；视觉

一切知识的特点就在于它的普遍可传达性，这是知识与质料性刺激所产生的情感、感受或情绪等的不同之处，因此，知识也就成为人作为超脱肉体性束缚的属灵存在的佐证。康德作为德国启蒙运动的主要代表人，弘扬的就是人的理性精神。然而，他首先面临着的是休谟问题的挑战，并基于此力图恢复纯粹理性的权威性。休谟损害了理性的纯粹性，其代表性观点是“个别偶然的事件重复一万次也是偶然的”，并以此来质疑因果律的客观有效性。休谟认为，因果性概念是这样形成的，即我们观察到事件b出现在事件a之后，并且这个过程持续了很多次，于是当事件a发生时，我们就习惯性地认为事件b也会出现，因果律也就变成了一种“心理上的习惯性联想”。因此，知识的客观有效性就变成了心理上的主观倾向，而这在康德看来是不能够容忍的，因为主观上的心理联想并不具有普遍必然性。康德认为，质料性的存在并不能为我们提供必然规律，由于受制于人的先天认知能力的局限性，一切对象都是表象，而自满自足意义上的物自体领域对于人来说是不可知的。于是认识论上的“哥白尼革命”便由此产生了，普遍必然性的根基由认知对象一端转移到了人的先天认识能力一端。这是康德在追求理性的超越性时面对人的有限性所不得不做出的妥协。康德认为，数学知识是通过纯粹生产性的想象力所构建起来的，因此，也就能够有效地贯通其普遍与特殊、概念与直观。数学的这种成功道路对于认知具有典型的示范作用。

具有普遍必然性的科学知识与数学知识在认识次序上也是有着一致之处的，两者都是借助于先天的理性在普遍中考察特殊，数学知识在面对特殊和个别对象时是以普遍的图型为标准的，“以至于正如这种个别在构造的某些普遍条件之下得到规定一样，概念的对象也同样必须被设想为普遍地得到规定，那种个别只是作为这概念的图型而与之对应的。”［1］553同时，哲学与数学知识这两者都需要在现象上进行经验性的运用，所以除了作为思维形式的概念，还要求一个相应的对象能够被给予，否则它就是无意义的。即使是先于对象的对于时空的纯粹直观，也只有借助经验性直观获得其对象后才具有客观有效性，因为它仅仅是经验直观的形式而已。“所以一切概念，以及和

一、数学作为一种成功的科学的示范作用

康德指出，真正的知识既不是一个单纯的先天命题，也不是单纯的经验命题，而是先天综合判断。加奎多（M.Giaquint)也指出，发现一个真理具有三个组成部分:首先，这个发现过程必须是独立的，也就是说人是本能地、自然而然地相信了真理的命题，而不是通过阅读这个命题或者被告知这个命题的方式来相信的；其次，对于这个真理的相信必须依靠一个可靠的路径；最后，对于真理的相信也不能够违背知识的合理性，即不能与人们预先拥有的认知状态相悖。总之，发现真理意味着以一种独立、可靠和理性的方式相信一个命题。［2］50因此，知识的获得也就需要一种明证性，这种明证性不是通过天赋观念或者是经验抽象所能够实现的。康德借助于数学知识的真理性来对此进行了解释。

康德在方法论中提出，数学在纯粹理性的拓展上首先开辟了一条比较成功的道路:“数学提供了一个没有经验的辅助而有幸自行展开来的纯粹理性的最光辉的例子……因此纯粹理性在先验的运用中希望能像它在数学中成功地做到的那样同样有幸彻底地扩展自己，尤其是当它在前者中应用的同一个方法在后者中已具有了如此明显的用处时。”［1］553数学家们不是在经验事物中总结出几何图形，而是以心中先天具有的几何图形去统摄经验事物，这也就使得哲学家眼前燃起了光明。人的理性就具有了本体论的意义，从而擎制着自然，担任审判者的角色，走在自然前边并强迫自然回答它的问题。

然而，知识也不能脱离经验，因为知识虽然不是来源于经验的，但却是始于经验的。康德认为，即使我们具有对概念详尽的定义，也并不能保证我们将概念应用于接受的对象。例如，我们可以彻底地描述一个两角形的定义，即一个被两条直线围绕而形成的平面图形，但这种定义显然不能使我们相信我们在直观中所表象出来的与概念恰当地相连。“如果我取消了使范畴作为一种可能的经验性运用的概念而突显出来的一切感性条件，而把范畴视为关于一般的物的（因而具有先验的运用的)概念，那么在这些范畴那里除了把判断中的逻辑机能看作事物本身的可能性条件之外就再也不能做任何事情了，却丝毫不能指明，这些范畴可以在哪里具有自己的应用和这种应用的客体，因而它们如何可以在纯粹知性中无须感性而具有任何一种意义和客观有效性。”［1］220

因此，我们必须讨论直观在数学概念形成中的作用。康德认为，我们可以通过在直观中建构出几何图形，以此来表象出特殊的几何图形所隶属的概念的普遍有效特征，通过这种方式我们获得了对几何学的先天综合知识。在方法论中，康德提出，只有在直观中将三角形的三个角与两个直角之和等同建立起来，才能将这种等同性合理地扩展到所有的三角形之上。首先，数学概念的图型是不能从经验中获得的，没有人能够实际地感知一种真正的欧几里德几何学上的直角三角形，因为这需要三条完美的直线，丝毫没有厚度，三条中的两条相交形成完美的直角。因此，如果想要在直观中来碰到它的话，就只能借助于想象力中或实际中的特殊图形。“所以我构造一个三角形，是由于我把与这个概念相应的对象要么通过在纯粹直观中的单纯想象，要么按照这种想象也在纸上以经验性的直观描绘出来，但两次都是完全先天地描绘，并没有为此而从任何一个经验中借来范本。个别被画出的图形是经验性的，却仍然用于表达概念而无损于其普遍性，因为在这个经验性的直观中被注意的永远只是构造这个概念的行动，对该概念来说许多规定如大小、边和角都是无关紧要的，因而这些并不改变三角形概念的差异就被抽象掉了。”［1］553几何图形或者是特殊对象的感觉印象，或者是想象力中的图像，但不管它是哪一种，我们从特殊几何图形上所反思出来的都是单一的对象。于是，我们就可以用一个绿色的等腰三角形表象出三角形的普遍概念，这个绿色等腰三角形就“作为一个概念（即一个普遍的表象)的构造而仍然必须在表象中表达出一个隶属于该概念之下的可能直观的普遍有效性”。［1］553我们在特殊的真实或者想象的三角形中反思出或者直觉出三角形的概念。里维斯（F.J.Leavitt)认为，反思的过程是这样的:我们对这个蓝色、三英寸高、等腰的三角的形象进行反思，并且将它的颜色、形状和等腰性去除掉，仅仅留下它的三角性。瑞斯杰德（Risjord.Mark)对之进行了更加详尽的补充:数学是对于直观或者纯直观的形式特征的研究，这种直观的形式是空间和时间。因此，数学最终是有关空间和时间的学科，它被视为是一种形式上的关系。［3］647-659

从这里我们可以看出，虽然我们是在对特殊三角形的特殊图像进行直观，但因为我们所关注的只是这种综合行动，也就是使我们能够经验一个三角形的时空直观之形式属性。这种在特殊中认识到的普遍性是通过纯直观的方式得到的。康德将属于知性和感性的东西从经验性直观中去除，从而得出了时间和空间这两种感性直观的纯形式，于是数学上构建的直观就从原始的时空中派生而出。

二、想象力在纯粹空间中所构建的数学知识

加奎多也指出，数学命题真理性只有通过视觉上的想象才能够得到证明，他进行了这样一个考察:想象一个正方形，它的四条边的每一条都有一个中点，将这四个中点相连接，构成了另一个正方形。水平地观察原来的正方形，新的正方形就像是倾斜的，有人会说“像一个菱形”（图1)。显然，原有的正方形要比包含在其内的倾斜的正方形要大。具体大多少？这需要借助视觉想象连同一些简单的推理来找到答案。

通过对图1的观察，我们可以清晰地发现原来的正方形是由倾斜的正方形同四个边角上三角形相加所组成的，这个倾斜正方形的每条边都是边角三角形的底边。现在我们想象将边角的三角形沿着倾斜正方形的边进行折叠。一般人都会得出这样的结论:边角三角形能够精确地覆盖住倾斜的正方形，既不会有任何微小的间隙，也不会有重叠。如果有人质疑这一点，那么可以想象将原来的正方形相对两边的中点连接起来（图2)，这样就将其划分为四个相等的小正方形，而倾斜正方形的四个边就是这些四等分正方形的对角线。因此，对边角三角形的折叠必定能够同倾斜正方形完全重合。

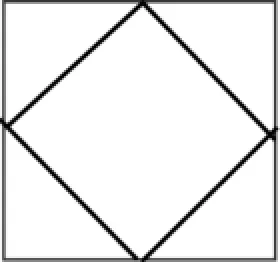
图1

图2

通过这样的视觉想象过程，人们发现既然边角三角形能够精确地覆盖倾斜正方形，那么边角三角形的总体面积与倾斜正方形的面积相等；原来的正方形的面积是由前两者构成的，那么原来正方形的面积也就等于倾斜内在正方形的两倍。通过这种方式，人们可以相信对于欧几里得空间中正方形的一个真实普遍的命题，即任何正方形。的面积是这样一个正方形面积的两倍，这个正方形的顶点为c的边的中点。［3］51这个证明过程也印证了康德对于几何学原理建立的观点:“几何学作为前提的少数几条原理虽然确实是分析的，并且是建立在矛盾律之上的；但它们正如那些同一性命题一样，也只是用于方法上的连接，而不是作为原则，例如a=a，即全体与自身相等，或（a+b)＞a，亦即全体大于部分。并且即算是这些原理本身，尽管仅仅按照概念来说就是有效的，但它们在数学中之所欲行得通，也只是因为它们能在直观中体现出来。”［1］13-14这也契合了加奎多用视觉想象操作和基本的理性推理对数学命题进行证明的基本途径。

这条数学命题的证明过程也就反映了数学知识是先天综合知识:首先，这条命题的真理性不是通过别人的灌输所保证的，而是通过每个人的空间想象过程再加上简单的理性推理所实现的；其次，这条命题的真理性也并不是通过从个别中抽象所实现的。因为正如上文中康德所分析的那样，标准的正方形和三角形只能够存在于心灵之中，而且我们无法以实际性操作来确定这条命题的真理性；最后，对于这条命题的相信也并不需要实际的感知经验。而几何命题的产生只需要通过想象力在纯粹空间中的活动即可实现，并不受制于处于特定时空中的具体事物的限制。柏拉图在《美诺篇》中就曾描写到，苏格拉底通过不断地提问和启发，使一个不具备任何几何学知识的童奴一步步得出了正确的解答。因此，柏拉图认为，人们在出生之前灵魂就已经具有了知识，只不过是灵魂与肉体相结合时被忘记了，学习就是把这些被遗忘的知识回忆起来。通过上面数学命题真理性的证明，我们也可以得出与柏拉图相似的结论，至少是在数学领域中，知识是通过内心的想象力构建起来的，其直观明证性不依靠经验事物，而是存在于作为人的先天认知形式的纯粹空间之中。正是这一点保证了数学知识既能够具有先天的普遍性，也能够落实到具体事物之中。

三、数学图型作为先验图型的类比

康德引入图型的概念也是为了建立起普遍与特殊之间沟通的桥梁:一方面，图型是种规则，它将条件具体化置入概念适用的对象直观之下；另一方面，它有指出具体直观对象的哪些特征是与普遍概念相连的。［4］128在讨论纯粹知性概念图型法的篇章中，康德认为存在着三种层次的概念:第一是范畴，也就是纯粹知性概念，是通过对判断的反思得出来的；第二层次是数学概念，包括几何学和代数概念；最后是经验的概念，比如盘子或者狗的概念。这三个层次在普遍性程度上逐步降低。

纯粹知性概念即范畴的图型被康德把握为是时间中的确定关系，因为先验的时间具有特殊的性质:它是一种统一整体的直观形式，而且先验时间规定之统一性还是范畴所构成的，因此就与范畴同质；另一方面，时间又是我们进行表象的纯粹时间形式，所以时间又是与现象同质的，因为如果不同质的话，现象也不会在时空形式裹挟之下进入我们的直观中来。所以，范畴通过对于时间性的规定而与经验联系起来。康德认为，纯粹知性概念与感性中的经验性直观是完全不同质的，必须借助于图型这个中介才能把后者归摄入前者之下，把前者应用于后者之上。因为范畴是通过反思人的判断能力所得出来的，所以与经验性直观肯定是完全不同质的。而且纯粹知性范畴的图型完全是想象力对于时间的规定性，“每一个范畴的图型都包含和表现着仅仅一种时间的规定，如量的图型，这就是在对一个对象的相继领会中时间本身的产生（综合)，质的图型，这就是感觉（知觉)与时间表象的综合，或时间的充实性，关系的图型，这就是诸知觉在一切时间中（即根据一条时间规定的规则)的相互关联性，最后，模态及其诸范畴的图型，这就是时间本身，作为对一个对象是否及怎样属于时间而加以规定的相关物。”［1］140对于这种先验图型我们是无法进行直观的，它只能够在经验世界中以现象事件的方式向我们展现出来，其自身不着痕迹。然而，通过数学图型，我们能够对先验图型进行类比。这是因为这两者都是生产性的想象力在纯粹时空中综合作用的产物。

康德认为，如果时空不是纯粹的话，那么数学也就不是纯粹的。也就是说，如果时空不纯粹的话，那么不管我们如何完全彻底地从图像中抽象并且仅仅关注构建的行为，得到的结果依然是经验的。数学概念作为时空概念，它们的纯粹性来自于时空的形式的直观，因为康德认为:形式的直观给出了表象的统一性，这种统一性的综合行为可能性的范围是在形式的直观中展示出的，倘若没有这种纯粹的形式的直观，经验的时间和空间直观也不会可能。“这种统一性，我在感性论中曾仅仅归之于感性，以便只注意到它是先行于一切概念的，虽然它是以某种综合为前提的，这综合不属于感官，但通过它，一切有关空间和时间的概念才首次成为可能的。”［1］107康德承认，通过想象力构建数学图型的活动能够使我们表象出时间和空间，认为如果我们“不从同一点设定三条线相互成直角，就根本不能表象空间的三个量度，甚至于，也不能表象时间，如果我们不是在引出一条直线（想要它作为时间的外部形象的表象)时只注意我们借以前后相继地规定内感官的那种对杂多的综合行动、并因而注意我们借以前后相继地规定内感官的那种对杂多的综合行动、并因而注意在内感官中这种规定的前后相继性的话”。［1］103正是通过数学图型，丝毫没有经验色彩的纯粹时空才能够被表象出来。

在康德看来，只有通过对我们在外部直观中的综合杂多进行空间方面的抽象，并且将关注点完全集中于综合行动本身和规定的前后相继，先验的时间才能够被表象出来。但时空的本源的形式的统一并不是来自于生产的想象力所构建的概念，因为像线段、小时之类的都是有特殊规定性的时间和空间，纯粹时空也是它们为了获得统一性所预设的，纯粹时空并不自身就是特殊的时空，所以也不能够以一种具体形态的方式被表象出来。像线段之类的想象力所构建的直观形象并不是时间的形式直观，而只是时间的图像类比。威克斯曼（Wayne Waxman)在《康德的心灵模式:对超验唯心主义的新解释》中说，虽然康德认为“外感官的一切量（quantorum)的纯粹形象是空间；而一般感官的一切对象的纯粹形象是时间”［1］141，但这里的形象有可能是象征的代名词，它类似于《判断力批判》中美的理念，也就是太宏大以至于无法构建起来的形象。不过，威克斯曼认为，有一点可以确认，那就是这种意义上的图像与数学家所建构的是绝对不同的。［5］122康德明确地提出，通过关注划线的行为所获得的时间的表象实际上仅仅是个类比:“而正因为这种内部直观没有任何形状，我们也就试图通过类比来补足这一缺陷，用一条延伸至无限的线来表象时间序列。”［1］36-37可见，直观中数学模型的构建只能以类比的方式表象时空，但不能成为时空的形式的直观的来源。反过来，纯粹形式的直观却是数学概念对经验客观有效性的必要条件，因为隶属于某个概念的某物必须能够在统治着我们感知的条件中被表象出来，具体地说也就是这样一个东西必须能够在包含着我们接受对象的空间中被表象出来。因此，数学概念只有通过在纯粹直观中的构建才被规定下来。数学图型根据数学概念在纯粹时空中的构建，也就启示了范畴图型在时间形式的纯粹直观中的构建。

以因果性这个纯粹知性范畴为例，其图型表现为杂多之物在时间上的接踵而至或相继状态。而它的直接表现是在经验世界中，比如作为原因的“太阳晒”与作为结果的“石头热”这两个事件的相继发生，或者“往杯子中倒水”与“杯子里的水位上升”这两个事件的相伴发生。因果性图型本身是不可直观的，但我们可以通过想象力在思想中引一条线的方式来类比它。实际上，这种时间规定的空间类比也是得到科学实验证明的。有研究发现，人们经常会将空间的长短来对应时间上的长短。而且人们生活中读书或写字时的习惯方向也会对时间的先后把握产生影响，习惯于从左往右进行书写的人会倾向于把左边把握为过去，而把右边把握为将来。而从右往左进行书写的人会有相反的时间把握倾向。［6］41-79这也证实了人们用空间来表征抽象的时间的心理倾向。

四、数学图型对于经验图型的示范作用

与纯粹知性范畴和直观之间的异质性不同，数学和经验概念与感性直观之间的联系是很紧密的:“一个盘子的经验性的概念和一个圆的纯粹几何学概念就具有同类性，因为在前者所思维的图形可以在后者中直观到。”［7］144首先，“圆”这个数学概念能够在直观中构建出圆形，“我们能够没有一切经验性的辅助单凭概念而使圆锥形被直观到，但这个锥体的颜色却必须先在这个那个经验中被给予出来。”［1］554而我们可以借助于这个在直观中构建出的圆形，来表象出在盘子这种经验性概念中思索出的圆形。因此，经验性概念与数学概念就是同质的，它们都与经验直观直接相连。纯粹知性范畴与经验和数学概念是不同质的，因为范畴是完全脱离直观而形成的思维形式，而数学概念虽然不是依靠经验直观而形成的，但它也必须在直观中构建自身。康德举了数学中的纯粹直观的例子，比如空间具有三个维度，以及两点之间只有一条直线。这样的原理是完全先天地在我们内心中所产生的，但如果我们不能够将它们应用于经验直观之上而显明含义的话，那么就会沦为无意义的。从这些分析我们可以看出，我们可以在具体的盘子中抽象掉如颜色、厚度和质地等其他一切感觉材料，这样留下的仅仅就是空间中的形状，而这恰恰能够在纯粹直观中以几何图形的形象被我们表象出来，我们也就理解了为何康德认为经验概念与数学概念是同质的。

经验概念的图型是生产想象力的经验性能力之产物，这意味着两点:首先，其形式不能违背先验逻辑，比如不能既是圆的又是方的；其次，它同时也具有经验性因素，与属于其概念的个别事物具有相似之处。一个经验性的对象的形象不足以为我们提供出适用于概念的稳固构架，反过来，“狗”的概念能够提供出“狗”的一种图型，这种图型适用于所有的具体的狗。“狗这个概念意味着一条规则，我们的想象力可以根据它来普遍地描画出一个四足动物的形状，而不局限于经验向我们呈现出来的任何一个惟一特殊的形状，也不局限于我能具体地表现出来的每一个可能的形象。”［1］40-141经验性概念的图型也是想象力在纯粹时空中所构建出来的规则或者图形，它不会是黑色的或者是白色的，因为对于颜色等刺激性的经验质料，康德并不认为具有普遍有效性，它们不能够在纯粹直观中展示出来:“因为只有大小的概念是可以构造、即可以先天地在直观中展示的，质却只能在经验性的直观中表现出来。所以没有人能够从任何别的地方、而只能从经验中取得与实在性概念相应的直观，但他也永远不可能先天地从自己本身中并先于经验性意识而分有这种直观。”［1］554康德因此也把“狗”的概念的图型视为是四足动物的形状，而没有添加更多的经验性质料描述，所以，“经验图式是类概念的图形化，是群体特征和结构的抽象化，人脑中有了它，便可认知属于某个类的个体……这个狗的图式在哪里呢？能否展现于直观之前呢？不能。它只是想象力的产物，你着力想象时，它似乎存在，一旦你去把握它，它就即刻消失。假如你把它画出来，它肯定不再是图式，而是一个具体事物的形象了。”［8］51-52

想象力是一种将不在场的事物复现出来的能力，而想象力所生产出来的图型也以空间化的方式连接概念与直观，因此，在认知过程中视觉起了不可替代的作用。科学研究证实，形状分析在人们对于物体识别的过程中起了相当关键的作用。实验表明，当一个新奇的对象被展示和命名，但并没有给出进一步的信息时（例如其作用)，两岁、三岁、五岁的孩子以及成人都依靠形状作为将这个事物的名字进行普遍化的根基。相反，当这个事物的质料上的功能重要性的信息被提供以后，成年人由通过形状命名转向通过事物的材料进行命名，但儿童却依然还是以形状来命名。［9］1-27这些研究证明，相比于质料上的功能来说，形式上的形状或轮廓对于孩子来说是识别事物或命名事物的主要依据。这也印证了康德的理论，即相比于后天获得的经验质料，纯粹时空形式才是人们生而俱有的先天认知机能。

最近，科学界提出的知觉符号理论也为图型的空间可视性提供了科学依据。知觉符号理论认为，概念认知表征与知觉表征是存在于人脑中同一神经系统之下的。研究者曾做过这样一个实验:被试者需要判断画中的物体是否在语言句子之中出现过，并对被试者的判断时间进行记录。实验结果表明，当画中物体在空间中的形状和方位与句子中隐含着的事物的形状和方位一致时，被试者的判断时间要明显快于画中和句子中形状方位不一致时。这个实验可以得出的结论是:在对概念进行认知的时候，相应地，头脑中对于这个事物在空间中的形状和方位的知觉（视觉)也被激活了。［10］153-156这也证实了经验事物的概念与经验事物的图型的天然联系。

康德只是指出心灵之中这些图型的存在，而并没有说明这些图型产生的来源。康德将图型称为是内心深处隐藏着的技艺。近代心理学家皮亚杰则试图为我们揭示出图型或图式的来源。他首先认为康德建立图型这种先天认知框架的路径是正确的:“看来在发生学上清楚的是，主体所完成的一切建构都以先前已有的内部条件为前提，而在这方面康德是正确的。”［11］104皮亚杰也认为，通过主体才建构出了认识的对象，这种建构是通过运算和结构的方式来综合所输入的材料的。皮亚杰将这种认识结构也归纳为各种各样的图式，还把同化和顺化过程作为认识发展的过程。他把认识视为是主客体相互作用的产物:“从一开始就既不存在一个认识论意义上的主体，也不存在作为客体而存在的客体，又不存在固定不变的中介物，那么，关于认识的头一个问题就将是关于这些中介物的建构问题:这些中介物从作为身体本身和外界事物之间的接触点开始，循着由外部和内部所给予的两个互相补充的方向发展，对主客体的任何妥当的详细说明正是依赖于中介物的这种双重的逐步建构。”［11］21-22皮亚杰认为，认识的图式并不是先天的，同时也不是通过后天的经验接受进来的，而是在儿童的活动过程中逐步发展建构而来的，是一种主动建构的辩证的动态过程。皮亚杰通过观察和实验不同阶段儿童的心理认知发展，提出了儿童的认知发展的阶段理论。他指出，在胚胎阶段有一种有机的结构，最初因为主客不分，没有客体存在的图式。而随着跟外部事物打交道的增多，就形成了多样化的图式，从开始的感知运动图式发展到永久客体的图式，后面的图式把前面图式包含在内。这样到了十四五岁时，人们的健全图式基本建构完成。皮亚杰通过认知发生的心理学揭示出了康德图型的隐秘的来源。

康德的图型学说是为了解决概念与直观之间的异质性而提出的不仅具有理论上的可信度，而且也被现代科学所证实，具有很重要的意义。数学图型作为先验图型与经验图型沟通的中介，也是认识过程中不可缺少的一环，而且对于科学知识的证明具有示范作用。数学图型向我们展示出了人的视觉化倾向，正是这种空间化表征和类比，使得人们能够将普遍和特殊更好地相结合起来。因此，数学知识的学习对于人们正确地使用概念和获得知识也是大有裨益的。

参考文献：

［1］〔德〕康德.纯粹理性批判［M］.邓晓芒，译.北京:人民出版社，2004.

［2］Giaquinto，M.Visual Thinking in Mathematics［M］.New York: Oxford University Press，2007.

［3］Leavitt，F J.Kant’s schematism and his philosophy of geometry ［J］.Studies in History and Philosophy of Science Part A，1991 （4).

［4］Risjord，Mark.The sensible foundation for mathematics:A defense of Kant’s view［J］.Studies in History and Philosophy of Science Part A，1990（1).

［5］Waxman，Wayne.Kant’s Model of the Mind:A New Interpretation of Transcendental Idealism［M］.Oxford:Oxford University Press，1991.

［6］Marta，C F，Time in language:Event duration in language comprehension［J］.Cognitive Psychology，2011（62).

［7］〔德〕康德.康德著作全集:第四卷［M］.李秋零，译.北京:中国人民大学出版社，2005.，

［8］曹俊锋.论康德的图式学说［J］.社会科学战线，1994（6).

［9］Landau，B，Smith，L，Jones，S.Object shape，object function，and object name［J］.Journal of Memory and Language，1998（1).

［10］Rolf，A Zwaan，Robert，A Stanfield.The effect of implied orientation derived from verbal contex t on picture recognition ［J］.American Psychological Society，2001（12).

［11］〔瑞士〕让·皮亚杰.发生认识论原理［M］.王宪钿，等，译.北京:商务印书馆，1981.

（责任编辑 方英敏）

中图分类号：B142

文献标识码：A

文章编号：1000-5099（2016）03-0006-06

DOI编码：国际10.15958/j.cnki.gdxbshb.2016.03.002

收稿日期：2016-02-25

基金项目：国家社科基金青年项目“康德想象力理论的现代价值研究”（15CZX033）。

作者简介：车 辕（1987—），男，山东泰安人，博士，助理研究员。研究方向：德国古典哲学。它们一起，一切原理，不管它们是多么先天可能的，却还是与经验性的直观、因而与可能经验的材料相关的。舍此它们就完全没有任何客观有效性，而只不过是游戏，不论是想象力还是知性各自用它们的表象所作的游戏。”［1］218正因为数学成功地为概念与其对象的联结提供了图型这一中介，因此，探讨想象力建构的数学图型能够启发我们认识到范畴和直观间借助图型的联结。