一种六自由度工业机器人运动学分析及三维可视化仿真

高　艺　马国庆　于正林　曹国华

长春理工大学，长春，130022



一种六自由度工业机器人运动学分析及三维可视化仿真

高艺马国庆于正林曹国华

长春理工大学，长春，130022

摘要：针对Motoman-HP20机器人的构型特点，采用D-H坐标变换法建立其运动学坐标系，将机器人分解为位置结构和姿态结构，得到以位置矢量和欧拉角表示的完备广义坐标，利用位姿分离法对机器人进行逆运动学求解，求得各个关键转角。构建了三维可视化仿真环境，验证所提出的运动学算法的正确性。该仿真环境可以直观地观察机器人各部分的运动情况。

关键词：工业机器人；运动学分析；可视化仿真；轨迹规划

0引言

从第一台机器人Unimate诞生至今，经过半个世纪的发展，工业机器人技术已相当成熟，重复定位精度高、运动速度快、程序柔性好等优点使其得到广泛应用[1]。但是市场上的商用工业机器人控制系统大都是对外封闭的，很少提供二次开发的接口，这给具有特殊作业要求的机器人系统开发和系统集成带来了困难。对工业机器人运动学的研究可以有效地了解机器人的奇异点的存在情况以及运动过程中的干涉情况，为轨迹规划提供技术基础，因此研究工业机器人的运动学问题非常必要[2-3]。

机器人的运动分析是实现机器人运动控制和轨迹规划的基础，它包括正运动学和逆运动学两部分。目前，机器人正运动学的求解方法主要有D-H坐标变换法和四元数法[4]；机器人逆运动学的求解方法主要有解析式法、几何法以及智能算法[5]。随着可视化技术的发展，越来越多的人将可视化仿真的方法应用于机器人的运动学求解，从而直观地监控机器人各关节的运动情况。Corke[6]开发了Robotics Toolbox机器人工具箱，该工具箱可实现机器人的运动仿真和轨迹规划，但其连杆不能表达真实机器人的三维尺寸，在碰撞检测方面的效果并不理想。李宪华等[7]以川崎FS03N机器人为研究对象，利用三维软件完成该机器人的实体建模，编写 SolidWorks软件和MATLAB的接口函数，构建基于MATLAB的3D仿真平台，通过运动仿真的方式验证了运动学的正确性。

本文以Motoman-HP20机器人为研究对象，采用D-H坐标变换法建立机器人的连杆坐标系，得到以位置矢量和欧拉角表示的正运动学方程，通过臂腕位姿分离法对机器人进行逆运动学求解，根据最短行程原则从多组逆解中选择出最适合的一组解。最后基于Dmworks软件构建三维可视化仿真环境，验证运动学求解的正确性。

1运动学求解

与动力学求解过程相比，运动学的求解过程并不考虑各杆件之间的相互作用力，只是研究其运动关系。正运动学问题是：在已知各关节角及杆件尺寸的基础上，求解工具坐标系在基坐标系下的位姿。逆运动学问题是：在已知工具坐标系相对于基坐标系的期望位姿和杆件的几何尺寸的情况下，求取机器人工具坐标系达到此位姿时各个关节的角度值。

1.1连杆坐标系的建立

Motoman-HP20是一款具有6个旋转关节的串联机器人，根据Motoman机器人的基坐标系设置原则和标准D-H坐标系建立准则，该机器人基坐标系x0y0z0的原点位于关节1的轴线上，同时也位于关节1轴线和关节2轴线的公垂线上，即二者的交汇处。依次建立各个关节处的坐标系，x6y6z6为机器人工具坐标系，其中后三个关节的坐标系交汇于一点。机器人D-H坐标系如图1所示。

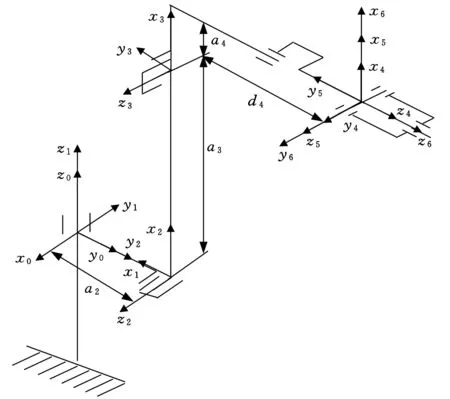
图1　Motoman-HP20机器人D-H坐标系

1.2正运动学求解

根据D-H坐标系建立准则可以确定图1中相邻两个坐标系之间的转换关系，同时根据该机器人的几何尺寸可确定机器人的D-H参数，如表1所示。对于关节型机器人而言，只有关节角βi为变量，两关节轴扭角αi、连杆长度ai、两连杆间偏置距离di均为常量。

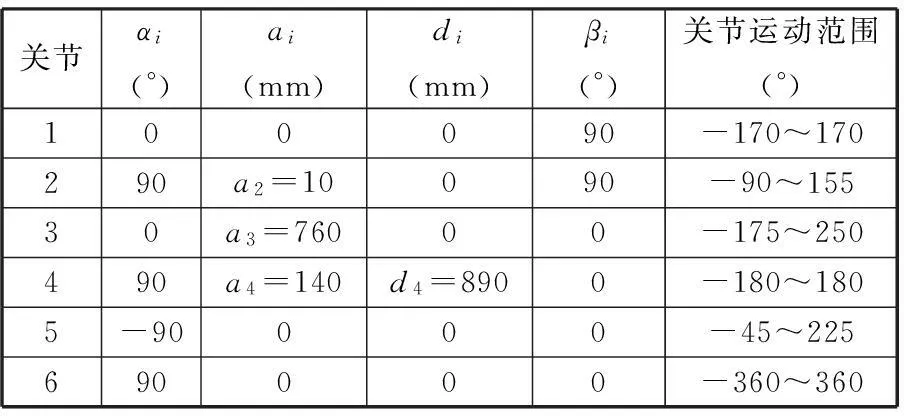
表1　HP20机器人D-H参数

机器人相邻关节坐标系间的转换矩阵[8]为

i-1Ti=Rot(z,βi)·Trans(0,0,di)·

Trans(ai,0,0)·Rot(x,αi)=

(1)

式(1)表示的是相邻两个坐标系之间的变换关系，将其顺次相乘可以得到工具坐标系在基坐标系下的变换矩阵：

(2)

nx=c1[c23(c4c5c6-s4s6)-s23s4c6]+

s1(s4c5c6+c4s6)

ny=s1[c23(c4c5c6-s4s6)-

s23s4c6]-c1(s4c5c6+c4s6)

nz=-s23(c4c5s6-s4s6)+c23s4c6

s1(s4c5c6-c4c6)

c1(s4c5c6-c4c6)

oz=-s23(c4c5s6+s4c6)-c23s5s6

ax=c1(c23c4s5+s23c5)+s1s4s5

ay=s1(c23c4s5+s23c5)-c1s4s5

az=s23c4s5-c23c5

px=c1(a4c23+d4s23+a3c2+a2)

py=s1(a4c23+d4s23+a3c2+a2)

pz=a4s23-d4c23+a3s2

ci=cosβi,si=sinβi

cij=cos(βi+βj)

sij=sin(βi+βj)

i=1,2,…,6;j=1,2,…,6

式(2)即为运动学正解，将表1中D-H参数代入式(2)可求得相应元素值。

由式(2)可以看出，该齐次变换矩阵包含了机器人工具坐标系到基坐标系的位姿信息，其中[noa]为姿态矩阵，p=(px,py,pz)为工具坐标系的位置矢量。用齐次变换矩阵表示刚体的转动虽然简化了运算，但需要9个元素来完全描述刚体的位姿，且它给出的是一组非完备的广义坐标。而在实际应用中工业机器人的位姿一般采用一组完备的广义坐标(px,py,pz,φ,θ,ψ)来表示。欧拉角的转动矩阵表达式为

(3)

s=sin,c=cos

令式(2)中的姿态矩阵与欧拉角的转动矩阵(式(3))的元素对应相等，得到一组完备的广义坐标(φ,θ,ψ)，求得

φ=arctan(ay/ax)

θ=arctan((axcφ+aysφ)/az)

ψ=arctan((nycφ-nxsφ)/(oycφ-oxsφ))

图1所示的位姿为HP20机器人的机械零位，但通过D-H法建立的坐标系关节角却为(90°，90°，0°，0°，0°，0°)，因此在构建三维可视化仿真环境的时候需要进行转换处理。

1.3逆运动学求解

根据HP20机器人构型特点，其后3个关节坐标系交汇于一点，故该机器人的位置仅由前3个关节变量决定，姿态仅由后3个关节变量决定。因此可采用位姿分离法来求解该机器人运动学的逆解。

(1)求解β1。将0T6=0T11T22T33T44T55T6左右两边各左乘(0T1)-1，则有

(0T1)-10T6=

(4)

令

(5)

取其中第4列

由于式(4)和式(5)矩阵第2行第4列对应相等，所以有

-s1px+c1py=0

(6)

则β1=arctan(py/px)。

(2)求解β3。由于式(4)和式(5)矩阵的第1行第4列及第3行第4列分别对应相等，所以有

c1px+s1py=a4c23+d4s23+a3c2+a2

(7)

pz=a4s23-d4c23+a3s2

(8)

对式(6)～式(8)分别取平方然后相加可得

μ=ρcosηc3+ρsinηs3

(3)求解β2。将0T6=0T11T22T33T44T55T6左右两边各左乘(0T11T22T3)-1，得

3T44T55T6=

(9)

令

(10)

其第3列和第4列元素分别为

由于式(9)和式(10)矩阵的第1行第4列及第2行第4列分别对应相等，所以有

a4=c1c23px+s1c23py+s23pz-a3c3-a2c23

-d4=-c1s23px+s1s23py+c23pz+a3s3+a2s23

β23=

可得β2=β23-β3。

(4)求解β4。由于式(9)和式(10)矩阵的第1行第3列及第3行第3列分别对应相等，所以有

c4s5=c1c23ax+s1c23ay+s23az

s4s5=s1ax-c1ay

当s5≠0时

当s5=0时，关节4和关节6重合，机器人退化为5自由度，此时，β4可以为任意值，一般定义为当前值。

(5)求解β5。将0T6=0T11T22T33T44T55T6左右两边左乘(0T11T22T33T4)-1，得

(11)

令

(12)

由于式(11)和式(12)矩阵的第1行第3列及第3行第3列分别对应相等，所以有

s5=ax(c1c23c4+s1s4)+ay(s1c23c4-c1s4)+azs23c4

c5=c1s23ax+s1s23ay-azc23

β5=arctan(s5/c5)

(6)求解β6。由于式(11)和式(12)矩阵的第2行第1列及第2行第2列分别对应相等，所以有

s6=nx(s1c4-c1c23s4)-ny(s1c23s4+c1c4)-nzs23s4

c6=ox(s1c4-c1c23s4)-oy(s1c23s4+c1c4)-ozs23s4

β6=arctan(s6/c6)

1.4解的对应关系

通过位姿分离变量法可得到该机器人的各关节角度值，共有可能的8组解。但是在实际的控制系统中，由于关节角度范围等因素的限制，实际只能取其中的一组作为最终的可行解。可行解的筛选原则主要有行程最短原则、能量消耗最小原则、运动最平稳原则等，结合HP20机器人构型特点，本文选取行程最短原则作为逆解筛选原则。最短行程原则算法流程如图2所示，其中βcm表示机器人当前第m关节的角度值，βnm表示机器人逆解第n组第m关节的角度值，n=1,2,…,8;m=1,2,…,6。

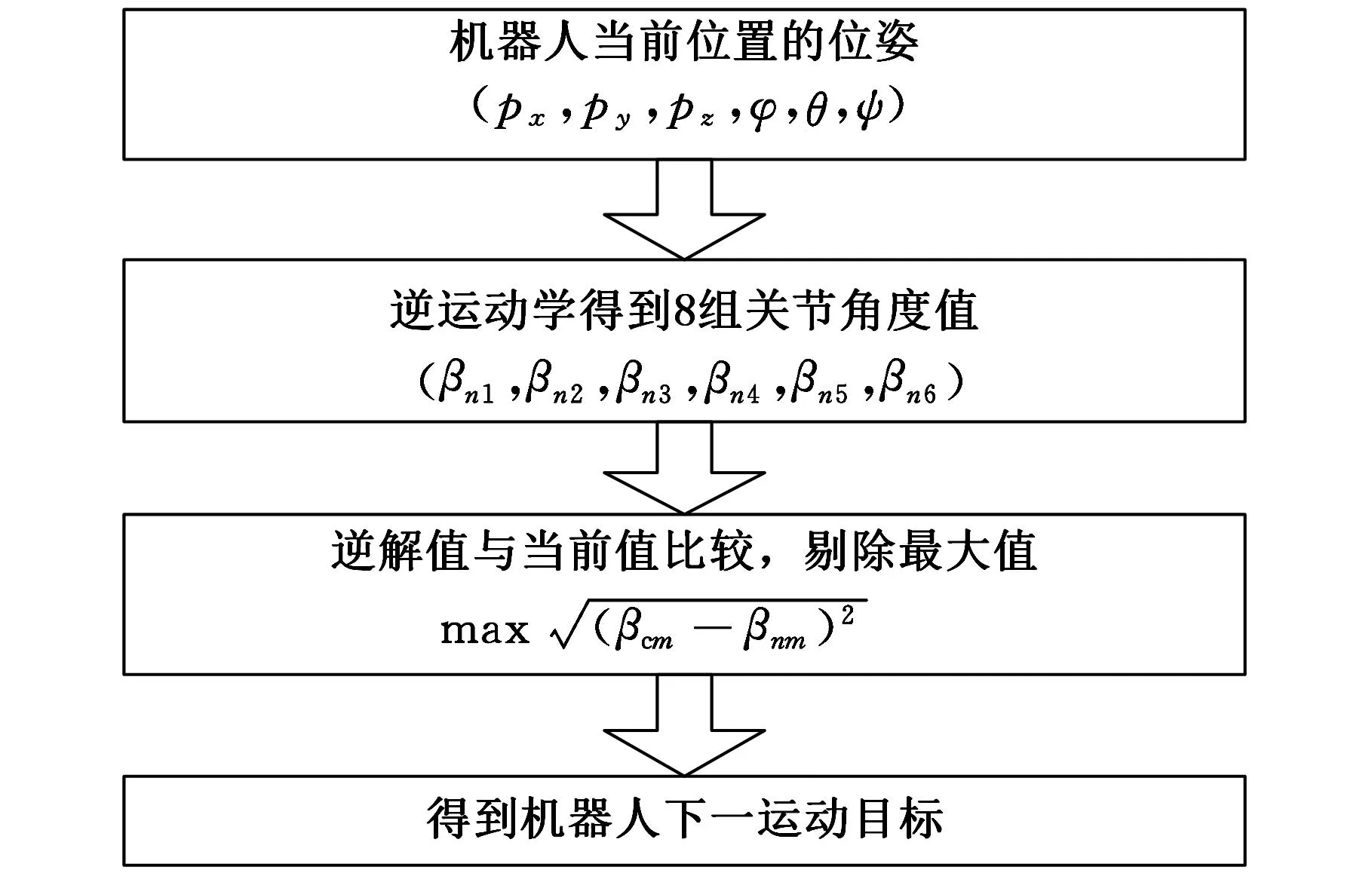
图2　最短行程原则算法流程图

2三维可视化仿真环境的建立

机器人三维可视化仿真是借助于计算机技术和三维建模技术构建起来的，它既能体现真实机器人的尺寸模型又具有真实机器人系统的运动学关系，可有效地验证运动学算法以及运动的可视化。

2.1三维模型的建立

三维建模软件具有强大的建模功能，可解决通用编程语言构建模型能力不强的问题，根据HP20机器人的特点，严格按照真实机器人的尺寸进行建模，将机器人模型分为7个部分，各部分如图3所示。

图3　机器人各部分模型

2.2三维可视化仿真环境的构建

将图3各部分模型分别导入DMworks软件，然后创建包含运动学关系的机器人设备，根据连接关系依次插入从而完成整个机器人设备的创建，然后设置关节类型和关节驱动、设置转角范围和工具中心点(tool center point, TCP)坐标，使其具有运动学的关系，三维仿真图形界面如图4所示。

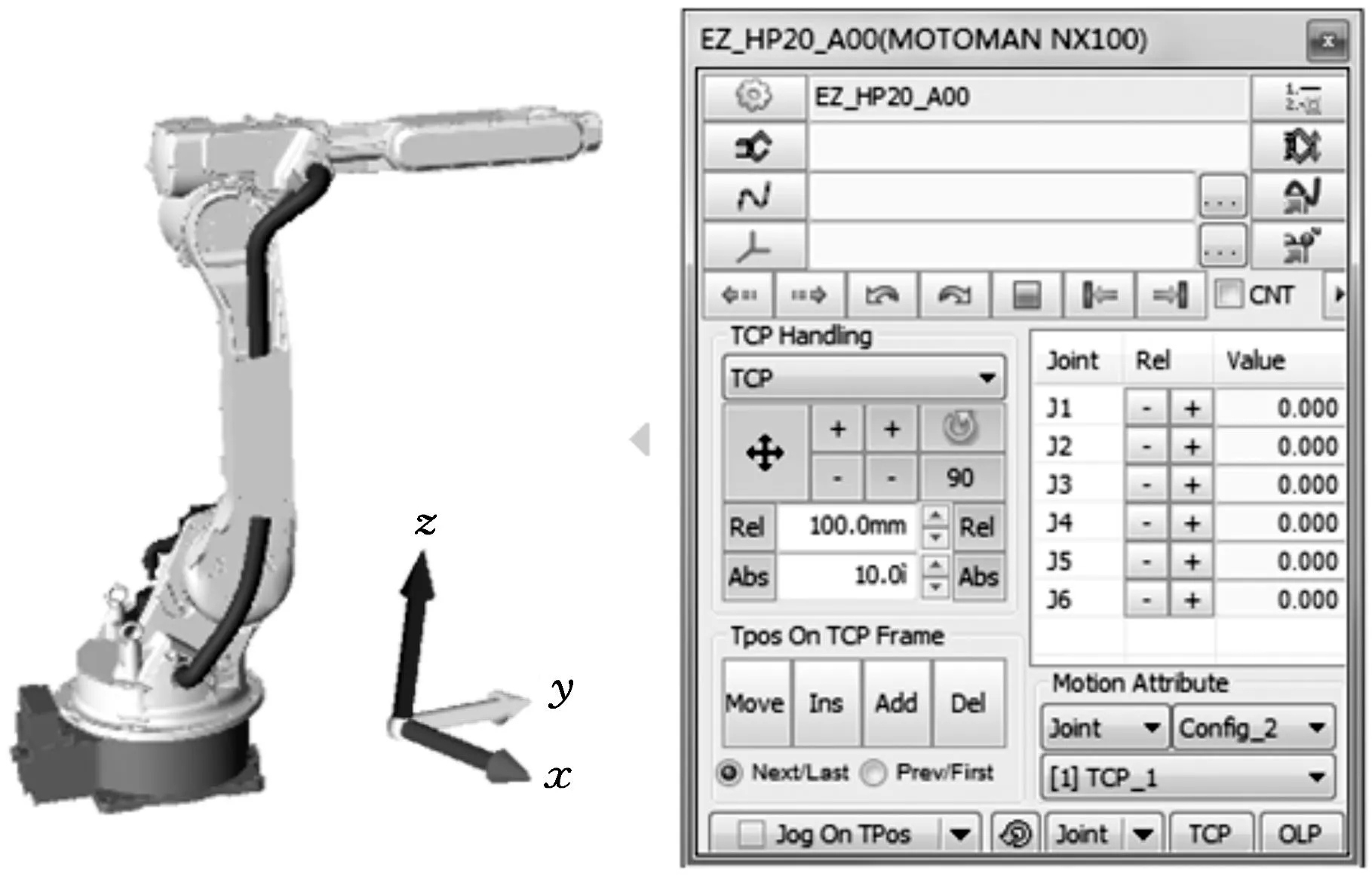
图4　三维可视化仿真界面

3基于三维可视化仿真的运动学算法验证

3.1正运动学算法验证

可视化仿真环境中机器人初始位姿为HP20机器人的机械零位，但通过D-H法建立的坐标系关节角却不全为0°，为使两者统一，在构建可视化平台时进行转换处理。图4中坐标指示方向与图1中基坐标系方向完全一致。在可视化仿真平台中选取5组特殊臂型来验证所提正运动学求解算法的正确性。5组臂型下机器人工具坐标系在基坐标系下位置矢量如表2所示，其臂型如图5所示。

表2　正运动学验证数据

图5　机器人几种臂型

由表2可看出： ①各关节角均为0°，处于机械零位，此时工具坐标系在基坐标系下位置矢量为(0，1050，900)mm;②其他关节为0°，第1关节为90°，此时工具坐标系在基坐标系下位置矢量为(-1050， 0，900)mm;③其他关节为0°，第2关节为90°，此时工具坐标系在基坐标系下位置矢量为(0，1050，-900)mm;④其他关节为0°，第3关节为90°，此时工具坐标系在基坐标系下位置矢量为(0，10，1660)mm;⑤其他关节为0°，第5关节为90°，此时工具坐标系在基坐标系下位置矢量为(0，945，1005)mm。

图5所示的臂型与表2中的数据一一对应，从而验证了所提出的运动学正解算法的正确性。

3.2逆运动学算法验证

逆运动学采用如下验证方法： ①随机取关节角为(30°，20°，-40°，-60°，50°，10°)的一组值，通过正运动学得到机器人此刻的位姿为(-438.301，898.477，57.334，-142.192，-62.472，33.366)mm；②将此组位姿值作为逆运动学求解的输入，得到机器人的可能存在的8组解；③将8组解逐组再用正运动学算法进行求解，得到每组关节角对应的位姿，对比每组关节角的姿态与原随机关节角输入时的位姿关系。

按照上述步骤得到8组关节角如表3所示，各组关节角对应的位姿如图6所示。每组关节角的姿态与原随机关节角输入时的位姿均相同，从而验证了逆运动学算法的正确性。

表3中给出了通过逆运动学求解得到的8组关节角，其中第3组关节5的角度、第5组关节2和关节5的角度以及第6组关节2的角度超出了表1中所给的对应关节运动范围，这说明虽然在理论上HP20机器人的运动学存在8组解，这是由于解反三角函数产生多解造成的，但是在实际系统中会因为电机转角限制、线缆缠绕、杆件干涉等因素导致表3中第3、5、6组关节角形成的位姿虽然在可视化仿真过程中可以显示，但现实中不能实现，这也恰恰说明了1.4节运用行程最短原则确定逆运动学的一组最优解的重要性。

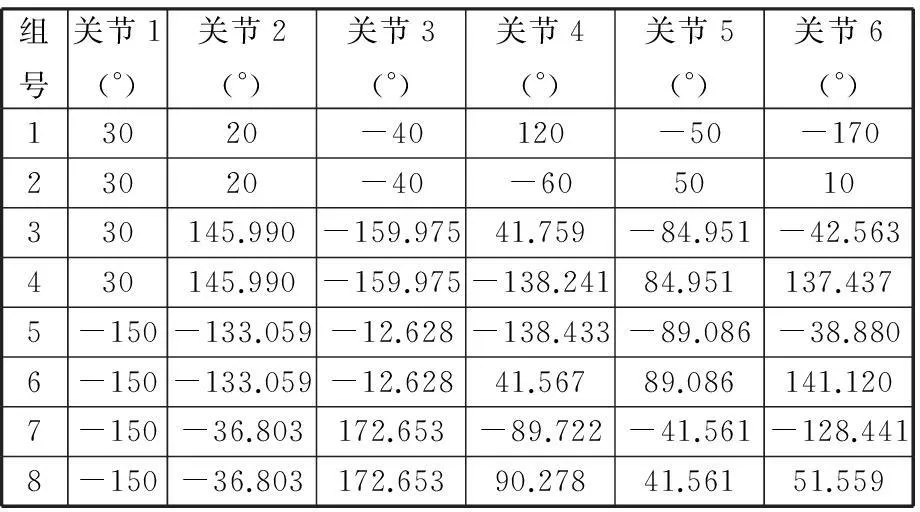
表3　HP20机器人逆运动学验证表

图6　运动学逆解8组位姿

4结束语

本文以Motoman-HP20机器人为研究对象，采用D-H坐标变换法建立机器人的连杆坐标系，得到了以位置矢量和欧拉角表示的正运动学方程，通过臂腕位姿分离法对机器人进行逆运动学求解，最后构建三维可视化仿真环境，验证所提出的运动学算法的正确性。该仿真平台可以直观地观察机器人各部分的运动情况，从而为后续可视化的轨迹规划奠定基础。

参考文献：

[1]王田苗,陶永. 我国工业机器人技术现状与产业化发展战略[J]. 机械工程学报，2014,50(9)：1-13.

Wang Tianmiao,Tao Yong. Research Status and Industrialization Development Strategy of Chinese Industrial Robot[J]. Journal of Mechanical Engineering, 2014,50(9)：1-13.

[2]Albu-Schaffe A，Haddadin S，Ott C H．The DLR Lightweight Robot: Design and Control Concepts for Robots in Human Environments[J]．Industial Robot，2007，34(5)：376-385．

[3]倪受东,张敏,盛志刚. 基于开放式平台的视觉工业机器人研究[J].制造业自动化，2014，36(2)：44-48.

Ni Shoudong, Zhang Min, Sheng Zhigang. The Research on Visual Industrial Robot Based on Open Platform[J]. Manufacturing Automation，2014，36(2)：44-48.

[4]何庆稀,游震洲,孔向东．一种基于位姿反馈的工业机器人定位补偿方法[J]．中国机械工程，2016，27(7)：872-876．

He Qingxi, You Zhenzhou,Kong Xiangdong. Positioning Error Compensation Method of Industrial Robot Based on Closed-loop Feed Back of Position and Orientation[J]. China Mechanical Engineering, 2016，27(7)：872-876．

[5]李瑞峰,马国庆. 基于MATLAB仿人机器人双臂运动特性分析[J].华中科技大学学报(自然科学版),2013,41(增刊1)：343-347．

Li Ruifeng,Ma Guoqing. Dual-arm Kinematic Characteristics Analysis of Humanoid Robot Based on Matlab[M]. J. Huazhong Univ. of Sci. & Tech. (Natural science Edition),2013,41(S1)：343-347．

[6]Corke P．Robotics，Vision and Control[M]．Berlin: Springer-Verlag，2011．

[7]李宪华,郭永存,宋韬．六自由度工业机器人手臂正运动学分析与仿真[J]．安徽理工大学学报(自然科学版)，2013，33(2)：34-38.

Li Xianhua, Guo Yongcun, Song Tao. Forward Kinematics Analysis and Motion Simulation Platform of a Six DOF Industrial Manipulator[J]. Journal of Anhui University of Science and Technology( Natural Science),2013，33(2)：34-38.

[8]蔡自兴.机器人学基础[M].北京:机械工业出版社，2009.

(编辑苏卫国)

收稿日期：2015-12-28

基金项目：国家高技术研究发展计划(863计划)资助项目(2013AA2400 )；吉林省科技发展计划资助项目(20100365 )；吉林省省级产业创新专项资金资助项目(2016C088)

中图分类号：TP242

DOI：10.3969/j.issn.1004-132X.2016.13.005

作者简介：高艺，女，1968年生。长春理工大学机电工程学院副教授。主要研究方向为机电系统控制理论与控制技术。马国庆，男，1988年生。长春理工大学机电工程学院助教、博士研究生。于正林，男，1971年生。长春理工大学机电工程学院教授。曹国华，男，1965年生。长春理工大学机电工程学院教授。

Kinematics Analysis of an 6-DOF Industrial Robot and Its 3D Visualization Simulation

Gao YiMa GuoqingYu ZhenglinCao Guohua

Changchun University of Science and Technology,Changchun,130022

Abstract:For configurational characteristics of Motoman-HP20 robot, the D-H coordinate transformation method was adopted to establish the kinematics coordinate system, the robot was decomposed into position structure and pose structure, complete generalized coordinates of position vector and Euler angle were obtained. Pose separation method was used to analyse the robot inverse kinematics solution for critical angle. The 3D visual simulation environment was built, and the kinematics of the proposed algorithm was proved to be correct. The simulation platform of robot movement of each part could be observed visually.

Key words:industrial robot; kinematics analysis; visualization simulation;trajectory planning