四轮驱动全轮差速转向移动焊接机器人运动学分析与仿真

毛志伟　吴　训　周少玲　李向春　邓凡灵

1.南昌大学，南昌，330031　　2.江西工业职业技术学院，南昌，330095



四轮驱动全轮差速转向移动焊接机器人运动学分析与仿真

毛志伟1吴训1周少玲2李向春1邓凡灵1

1.南昌大学，南昌，3300312.江西工业职业技术学院，南昌，330095

摘要：为增加轮式移动焊接机器人稳定性、负载能力和降低控制复杂度，提出了一种四轮驱动全轮差速转向移动焊接机器人机构，介绍了该机构差速转向原理，证明该机构无转向侧滑。采用非完整约束方法建立了其差速转向误差模型，并在该模型基础上对其进行了直线-圆弧-直线轨迹数值仿真，结果为转角误差0.002 137°，转动中心坐标误差小于0.012 mm。仿真结果表明该模型满足焊接中的位置精度要求。

关键词：四轮驱动移动机器人；全轮差速转向；运动学模型；数值仿真

0引言

轮式移动机器人具有结构简单、状态稳定等特点，已经广泛应用于机械工业等领域[1-2]。目前四轮轮式移动机器人转向主要有滑移转向、四轮驱动和四轮独立转向三种方式[3]。滑移转向不需要单独设计转向机构，通过两侧轮子速度差来实现(如四轮驱动滑移转向移动机器人)，该方式由于存在侧滑，其转向精度和稳定性难以保证。四轮转向方式一般应用在新型汽车中，这种方式操作方便，但结构较为复杂[4]。四轮独立转向能使转向更为精确，Fischer等[5]针对较薄钢质液化储罐采用了四轮驱动四轮独立转向机器人；杨树风[6]研制的一款带有机械手臂的四轮全方位移动机器人亦是此种结构，但该转向方式需要更多电机驱动，且控制复杂。

笔者在对各种转向移动机器人分析的基础上，结合焊接实际需要，提出了一种四轮驱动全轮差速转向移动焊接机器人[7]，该机器人机构采用全轮转向原理，左右两侧的转向各由一个电机驱动，且前后轮转向角度大小相等，方向相反。该转向方式可避免机器人转向时侧滑，机器人转向精度与稳定性高，能满足移动焊接要求。

为验证机构正确性及为后续分析奠定基础，分析了该机构无侧滑条件，并建立了其运动学模型与误差模型，采用MATLAB软件以典型的直线-圆弧-直线焊缝为例进行了轨迹仿真分析。

1四轮驱动全轮差速转向机构及原理

四轮驱动全轮差速转向移动焊接机器人四轮驱动原理见图1，其中移动焊接机器人主要结构包括4个驱动轮(驱动轮1～4)，机器人本体5以及焊枪等。其运动副主要包括4个驱动轮绕各自轴的旋转副，4个驱动轮与机器人本体5之间的旋转副，以及驱动焊枪的十字滑台中2个移动副。移动焊接机器人差速转弯时左边驱动轮的转弯半径如图1中RL所示，右边驱动轮的转弯半径如RR所示。

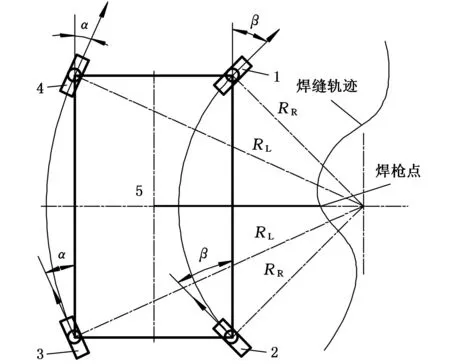
图1　四轮驱动机器人差速转向原理图

四轮驱动全轮转向移动机器人差速转向时，驱动轮1与驱动轮2的速度vR大小与偏转角β大小分别相同，但两轮的偏转角方向相反；驱动轮3、驱动轮4的速度vL大小相等，偏转角α大小相同方向相反。设速度差Δv=vR-vL=0时，移动机构将沿直线运动；Δv<0时，移动机构将绕右侧转动中心转动(图1)；Δv>0时，移动机构将绕左侧转动中心转动。四轮差速转向的特点是左侧前后两轮的速度vL大小、偏转角β大小始终相同，右侧两轮的速度vR大小、偏转角α大小始终相同，利用两侧轮子差速能实现绕任意半径转弯，转向灵活、精度高、操作简便、结构简单，且无需转向机构。

2无侧滑条件及误差模型的建立

2.1移动机器人无侧滑条件

本文所提出的机器人机构转弯时虽然不存在侧滑，但必须满足一定的条件。下面就该机器人无侧滑条件进行分析。

移动机器人转弯时，4个驱动轮状态及坐标系oxy如图2所示。左右两侧前后车轮转角大小相等，方向相反。E为机器人质心，H为焊接点，O1为H点处焊缝轨迹曲率中心，A、B、C、D为各驱动轮与机器人本体间转动副中心，F为AB中点，G为AD中点。设：LHO1=R0， LEH=d，LAD=LBC=2l，LAB=LCD=2b。H点坐标为(xH,yH)、速度为vH，vH与x轴夹角为θH，左侧前后轮当前转角为α，右侧前后轮当前转角为β，EH与x轴夹角为θ，AH与AB间夹角为φ。

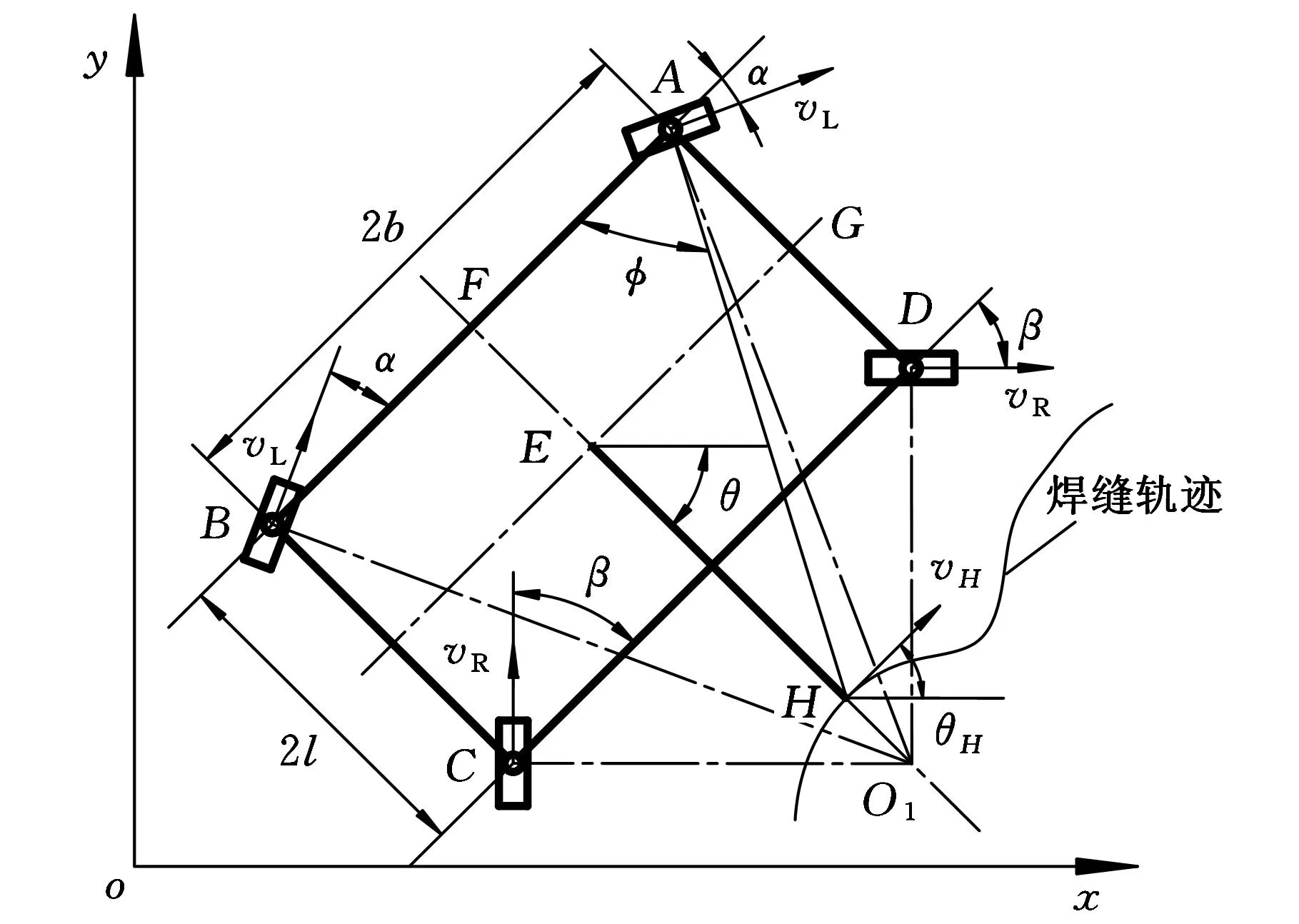
图2　机器人无侧滑差速转向坐标系

根据无侧滑条件可得机器人的质心方程：

(1)

相关约束条件如下。

(1)几何约束：

(2)

(2)焊接约束。根据焊接工艺要求，焊接过程中vH沿焊缝轨迹切线方向大小不变，故有

(3)

(4)

(3)无侧滑约束条件。机器人转弯时若无侧滑，则各轮沿机器人本体转动半径方向上的速度为0。以左侧前轮为例有

(5)

其中，(xF,yF)为左侧前轮中心点坐标。

机器人质心约束条件为

(6)

(4)由左前轮中心与H点几何关系及式(6)可得

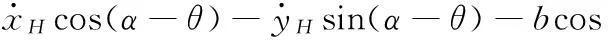
(7)

结合式(3)、式(4)可知，式(7)恒成立，说明该机构不存在滑移现象。

2.2四轮差速转向移动机器人误差模型

机器人差速转向误差模型如图3所示：机器人质心的初始位置与水平线的夹角为θc，机器人下一个运动状态时质心与水平线的夹角为θr，(xc,yc)是初始焊枪点的位置坐标，(xr,yr)为下一运动状态时焊枪点的位置坐标，xe为当前时刻小车焊枪点相对上一时刻焊枪点在x方向的误差，ye为当前时刻小车焊枪点相对上一时刻焊枪点在y方向的误差。

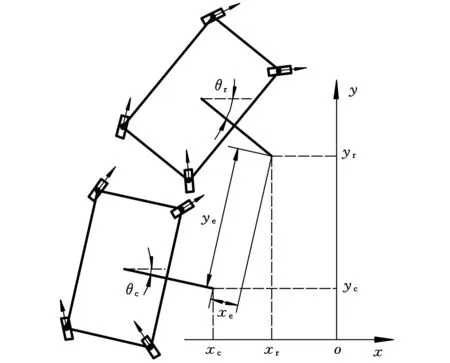
图3　差速转向误差原理图

由图3得到机器人的误差模型：

由文献[8]可得机器人误差微分方程：

3无侧滑差速转向运动仿真与分析

为验证上述无侧滑条件及差速转向误差模型的正确性，以机器人误差模型为基础对给定直角圆弧轨迹转向进行数值仿真分析。仿真参数设定如下：vH=10mm/s，d=400mm，l=75mm，b=90mm，给定轨迹的直线距离a=1000mm;给定轨迹的圆弧半径R0=800mm，如图4所示。

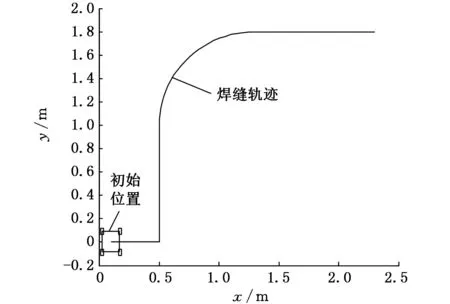
图4　机器人的初始位置及焊缝轨迹

采用齐次坐标变换法，对机器人机构进行逆运动学求解，将机器人移动机构沿直线-圆弧-直线轨迹运动分解为第一段直线运动、圆弧运动及第二段直线运动，特别是在圆弧运动过程中通过运动学逆解求解出各驱动轮的角速度ω及偏转角度θ。

运用MATLAB软件对上述轨迹进行运动仿真，结果如图5所示。机器人理论轨迹与仿真轨迹对比如图6所示。

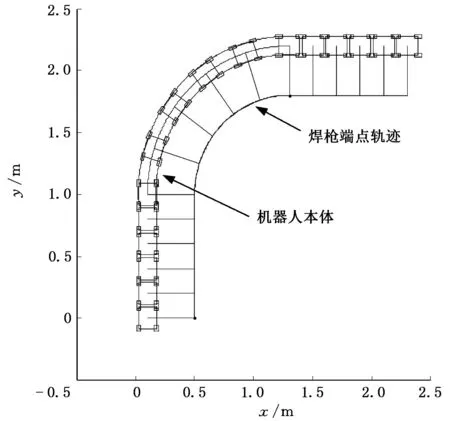
图5　机器人的运动仿真过程

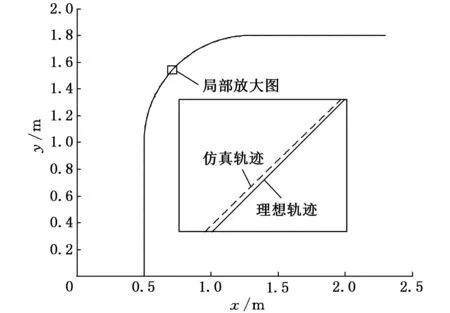
图6　理论轨迹与仿真轨迹分析

机器人在运动仿真中经过圆弧后质心的坐标为(1299.90,2199.91)mm，理论坐标值为(1300,2200)mm，误差为(-0.10,-0.09)mm。焊接点的坐标为(1299.77,1799.91)mm，理论坐标值为(1300,1800)mm，误差为(-0.23,-0.09)mm。轨迹跟踪后，得到焊枪到圆心的轨迹距离、转动中心坐标及转角的误差。焊枪到圆心的距离为800mm，与设定的R0=800mm一致。转动中心坐标为(-0.000 037，0.000 037)mm，转角误差为0.002 137°，仿真轨迹与理论轨迹基本重合。

仿真误差的来源主要有：①机器人转弯时前后轮转向的角度分别为α和β，而在MATLAB仿真时对这两个角度的初始值给定的精度可能不够；②仿真仅考虑了运动学分析，未考虑到动力学特性，实际运动可能还要考虑惯性、偏心、摩擦等；③MATLAB软件仿真时软件本身产生的误差等。

由上述分析可知，焊枪到圆心的距离误差及转角的误差已基本消除，转动中心的坐标误差也在0.012mm以下，达到了焊接中的位置要求。仿真得出了机器人移动机构的运动轨迹,并将运动轨迹与目标轨迹进行了对比,得到了两者的偏差,验证了全轮差速转向机构的运动精确性。

4结论

(1)对提出新型四轮驱动全轮差速转向移动

机器人，采用非完整约束法建立了机器人的运动学模型，证明其满足无侧滑转向时的约束条件。

(2)建立了该机器人机构的运动学误差模型，采用MATLAB软件以典型直线-圆弧-直线焊缝轨迹为例进行数值仿真，得到其转角误差为0.002 137°，转动中心的坐标误差小于0.012mm，验证了其运动学及误差模型的精确性，为该机构的进一步分析及控制提供了依据。

参考文献：

[1]李晓延，武传松，李午申. 中国焊接制造领域学科发展研究[J].机械工程学报，2012，48(6):19-31.

LiXiaoyan，WuChuansong，LiWushen.StudyontheProgressofWeldingScienceandTechnologyinChina[J].JournalofMechanicalEngineering, 2012，48(6):19-31.

[2]张轲，吕学勤，吴毅雄. 移动焊接机器人的研究现状及发展趋势[J]. 焊接，2004(8):5-9.

ZhangKe，LüXueqin，WuYixiong.ResearchStatusandDevelopmentTrendaboutMobileWeldingRobots[J].Weling&Joining, 2004(8):5-9.

[3]朱磊磊，陈军. 轮式移动机器人研究综述[J].机床与液压，2009，37(8):242-247.

ZhuLeilei，ChenJun.AReviewofWheeledMobileRobots[J].MachineTool&Hydraulics, 2009，37(8)，242-247.

[4]黄孝奎. 四轮转向汽车控制研究及动力学仿真[D].沈阳:东北大学，2008.

[5]FischerW,TacheF,SiegwartR.MagneticWallClimbingRobotforThinSurfaceswithSpecificObstacles[C]//6thInternationalConferenceonFieldandServiceRobotics.Chamonix,2007:1-8.

[6]杨树风.带有机械臂的全方位移动机器人的研制[D].哈尔滨, 哈尔滨工业大学，2008.

[7]毛志伟，周少玲，石志新,等. 移动焊接机器人四轮驱动差速转向方法:中国，102991578.A[P].2013-03-27.

[8]AngelesJ.机器人机械系统原理：理论、方法和算法[M]. 宋伟刚,译. 北京：机械工业出版社，2004.

(编辑王旻玥)

收稿日期：2015-09-01

基金项目：国家自然科学基金资助项目(51265036)

中图分类号：TH242

DOI：10.3969/j.issn.1004-132X.2016.13.006

作者简介：毛志伟，男，1969年生。南昌大学机电工程学院副教授。主要研究方向为焊接自动化与机器人。发表论文30余篇。吴训，男，1990年生。南昌大学机电工程学院硕士研究生。周少玲，女，1968年生。江西工业职业技术学院副教授。李向春，男，1990年生。南昌大学机电工程学院硕士研究生。邓凡灵，男，1990年生。南昌大学机电工程学院硕士研究生。

Kinematics Analysis and Simulation for Four Wheel Drive All WheelDifferential Steering Mobile Welding Robots

Mao Zhiwei1Wu Xun1Zhou Shaoling2Li Xiangchun1Deng Fanling1

1.Nanchang University, Nanchang, 330031 2.Jiangxi Industry Polytechnic College, Nanchang, 330095

Abstract:In order to raise the stabilization,load capacity of mobile welding robots and to reduce the control complexity,a four wheel drive all wheel differential steering mobile welding robot mechanism was proposed.The differential steering principles of this mechanism were introduced and proved this mechanism had no sideslip.The differential steering deviation model was built with nonholonomic constraint method.Based on this model,a numerical simulation analysis of straight-arc-straight trajectory was presented.As results,the rotation angle deviation is as 0.002 137° and the deviation of rotation center is under 0.012 mm.The simulation results indicate that the model satisfies the position accuracy requirements.

Key words:four wheel drive mobile robot;all wheel differential steering;kinematic model;numerical simulation