基于多目标遗传算法的贝塞尔超声变幅杆优化设计方法研究
纪华伟 赵双双 胡小平
杭州电子科技大学,杭州,310018
基于多目标遗传算法的贝塞尔超声变幅杆优化设计方法研究
纪华伟赵双双胡小平
杭州电子科技大学,杭州,310018
摘要:为设计满足蜂窝复合材料加工要求的高性能超声变幅杆,提出了一种基于多目标遗传算法的超声变幅杆优化设计方法。以变幅杆的结构参数为设计变量,以谐振频率和放大系数为优化设计目标,建立了贝塞尔超声变幅杆的数学优化模型。通过在遗传算法中调用ANSYS仿真软件,对变幅杆进行了建模和动力学分析,获得了计算目标函数所需的参数,采用多目标遗传算法求出了Pareto最优解集,在所求出的Pareto最优解集中选择了一组最符合设计要求的解作为超声变幅杆的设计参数。为验证设计的有效性,对所设计的变幅杆进行了性能测试并对蜂窝复合材料进行了试切实验。实验结果表明:通过该优化设计方法得到的变幅杆放大倍数为7.66,较优化设计前提高了29%,且工作频率更接近于设计频率。通过仿真分析和性能实验,验证了该方法的有效性和可靠性,试切实验结果表明所设计的变幅杆满足加工要求,工艺效果好。
关键词:贝塞尔超声变幅杆;多目标优化;遗传算法;蜂窝复合材料
0引言
蜂窝复合材料具有高比强度和高比刚度等优点,在航空航天领域得到了越来越广泛的应用,并不断向新领域扩展。传统方法在加工蜂窝复合材料的过程中,存在加工零件表面质量差、尺寸精度低和加工粉尘大等问题。超声切割加工作为加工蜂窝复合材料的一种较好的方法,有着广泛的应用前景[1-2]。超声切割加工装置主要由超声电源、换能器、变幅杆和工具头组成。从超声电源发出的超声频电振荡信号由换能器转换为超声频机械振动后传递到变幅杆,再由变幅杆将振幅放大后传到工具上,工具与蜂窝材料之间发生间断性冲击与分离,使材料发生分离。超声变幅杆的主要作用,一是将机械振动位移或速度放大,把能量集中在较小的辐射面上进行聚能;二是作为机械阻抗的变换器,在换能器和声负载之间进行阻抗匹配,使超声能量由换能器更有效地向负载传输[3]。蜂窝复合材料的超声切割加工系统不同于一般的超声辅助加工系统,为达到蜂窝复合材料冲击分离的目的,并保证零件的加工质量和效率,工具端部的振幅要达到10~50 μm,而一般的超声换能器的输出振幅为2~10 μm,因此,需要采用具有较大变幅能力的变幅杆以获得满足工程需要的振幅。
目前,对指数形、圆锥形以及阶梯形等简单形状变幅杆的设计、优化和仿真分析的研究较多,且优化目标较为单一[4-8]。对于蜂窝复合材料的加工,需要较大的放大系数和稳定的工作频率,简单形状的变幅杆无法较好地满足加工需求。指数形和圆锥形变幅杆的放大系数较小,工具端部振幅达不到加工要求;阶梯形变幅杆虽然放大系数较大,但它在截面突变处会产生应力集中,导致工作过程中截面突变处温度较高,不适合长期工作。贝塞尔曲线形超声变幅杆与圆锥形和指数形变幅杆相比,放大系数较大,与阶梯形变幅杆相比,不会出现应力集中现象,应力分布较均匀。但是,由于贝塞尔曲线形变幅杆形状复杂,有多个结构参数,每个参数都会对其性能产生影响,如何统筹兼顾各个参数,使之达到最佳的工作性能,是这种变幅杆设计的关键。目前,对贝塞尔曲线形超声变幅杆的设计以经验设计、仿真分析和反复修正为主,设计效率低,设计精度差。
本文以贝塞尔曲线形变幅杆为对象,研究基于多目标遗传算法的变幅杆的优化设计方法及其关键技术。首先,以变幅杆的结构参数为设计变量,以谐振频率和放大系数为优化设计目标,建立超声变幅杆的数学优化模型,进而利用NSGA-Ⅱ多目标遗传算法对变幅杆进行优化设计,最后,对所设计的变幅杆进行性能测试以及对蜂窝复合材料进行试切实验,以验证优化方法的正确性。
1变幅杆的参数化建模与动力学分析
在工程应用中,由于多目标优化问题的复杂性,目标函数所需参数往往很难通过数学计算得到,必须借助于有限元计算程序。ANSYS自带的APDL是一种可通过参数化变量方式建立分析模型并可自动完成有限元分析的脚本语言,是完成优化设计的基础。因此,本研究采用APDL和命令流相结合的方法,建立了贝塞尔曲线形变幅杆有限元参数化模型,在此基础上利用ANSYS对模型进行动力学分析(包括模态分析和谐响应分析),并提取影响变幅杆声学性能的谐振频率和放大系数作为优化目标。
以三次贝塞尔曲线作为超声变幅杆的母线形状,如图1所示,P0、P1、P2、P34个控制点在平面中定义了三次贝塞尔曲线,(X,Y)为控制点坐标。根据工程中所用换能器的辐射面面积和工具头的大小,确定变幅杆的大小端半径R和r,依据半波长理论确定变幅杆长度L。

图1 三次贝塞尔曲线及参数
经过理论计算和分析,贝塞尔曲线形变幅杆的相关结构参数和初值如表1所示。

表1 各结构参数及其初值 mm
基本参数确定后,建立变幅杆有限元模型,对变幅杆进行模态分析和谐响应分析,得到变幅杆的纵振频率和振型,从而了解变幅杆的振动特性。谐响应分析用于确定变幅杆在承受随时间按正弦规律变化的载荷时的稳态响应,以获得变幅杆振幅放大系数。由分析结果可知,变幅杆谐振频率为21.671kHz,与系统工作频率20kHz偏差较大,放大系数为5.93,需进行优化设计以满足加工要求。
2优化模型的建立
2.1设计变量
在优化过程中,R、r和L作为已知量,P0和P3固定,P1和P2在图1所示的虚线框中运动,由于这两点的位置直接决定曲线的形状,进而影响超声变幅杆的声学性能,因此,将P1和P2的坐标作为设计变量,即
X=(X1,X2,Y1,Y2)
(1)
2.2目标函数
谐振频率是超声变幅杆的重要性能参数,只有变幅杆的谐振频率等于系统工作频率,产生共振,才能在输出端产生最大的振幅。若其与系统工作频率差别过大,不仅会影响超声切割加工的质量,还可能导致超声声学系统的破坏,甚至损坏超声电源[8]。放大系数是超声变幅杆工作在谐振频率时,输出端与输入端的质点位移的比值,其大小将直接影响加工的效率和加工质量。为了提高超声变幅杆的综合性能,将其谐振频率和放大系数作为优化目标,优化时,超声变幅杆的谐振频率越接近系统工作频率越好,放大系数越大越好,而遗传算法优化是求极小值的,所以建立的多目标优化函数如下:
(2)
式中,fr为变幅杆的谐振频率;f为超声加工系统的工作频率,本研究根据实际加工需要,所用工作频率为20 kHz;M为变幅杆的振幅放大系数。
2.3约束条件
此约束为边界约束,变幅杆的结构参数在一定范围内取值,这里选取优化变量的范围为
(3)
3多目标遗传算法优化求解与优化结果分析
传统的多目标优化方法如加权组合法、目标规划法等都是通过某种数学变换将多目标转化为单目标进行求解,这种方法在工程应用中往往受设计人员主观因素的影响,很难取得最优解[9]。Deb等[10]提出的NSGA-Ⅱ多目标遗传算法是目前公认的最为有效的求解多目标优化问题的算法之一。NSGA-Ⅱ的主要思想是:利用非支配排序算法对种群进行非支配分层,然后通过选择操作得到下一代种群,使用共享函数的方法保持群体的多样性。相比其他优化方法,NSGA-Ⅱ有如下优势:计算复杂性降低,能够更好地保持种群的多样性和避免优秀个体的流失,而且无需主观地设定一些算法参数,从而进一步提高计算效率和算法的鲁棒性;该算法求得的Pareto最优解分布均匀,收敛性和鲁棒性好;该算法一次运行可以获得多个Pareto最优解,决策者可以根据系统的实际要求选择最终的满意解,为各目标之间的权衡分析提供了有效的工具。
本文以MATLAB高级语言为平台编写多目标优化程序,反复调用ANSYS批处理模式自动完成变幅杆的建模和动力学分析,以获取计算目标函数所需的参数。要想实现MATLAB对ANSYS的调用,必须先实现两者的数据传递,而它们都有较强的文件操作能力。同时,ANSYS软件提供了批处理运行方式,即在不打开软件的情况下可以在后台运行计算并输出结果,这使得在遗传算法程序中可以调用ANSYS进行数据传递,数据流向如图2所示。
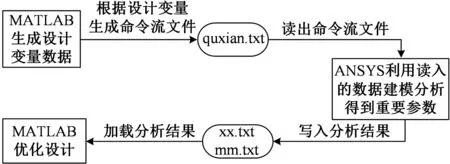
图2 MATLAB与ANSYS的数据传递
本文采用谢菲尔德(Sheffield)大学的遗传算法工具箱,通过MATLAB高级语言编写优化程序。采用遗传算法对贝塞尔曲线形变幅杆进行多目标优化设计,流程如图3所示。

图3 遗传算法优化流程图
考虑到实际加工过程对振幅和频率的实际要求,式(2)中f1(x)和f2(x)的权重系数均取0.5,利用权重系数法,借助NSGA-Ⅱ多目标遗传算法求解多目标优化模型,选定初始种群规模为30,经过40次遗传算法迭代得到超声变幅杆结构参数的多目标Pareto最优解,优化前后设计变量值如表2所示,变幅杆母线形状如图4所示。

表2 优化前后设计变量值 mm

图4 优化前后变幅杆母线形状
应用有限元分析软件ANSYS对优化后的超声变幅杆进行动力学分析,优化后,变幅杆的谐振频率为20 kHz,等于系统工作频率;变幅杆放大系数为7.92,比优化前的5.93提高了约34%。通过本方法对超声变幅杆进行优化设计,不仅使其谐振频率更接近其工作频率,还使得振幅放大系数得到显著提高。
4实验测试
为了验证本研究所提出的变幅杆的优化设计方法的正确性,利用316不锈钢加工了优化后的贝塞尔曲线形变幅杆。考虑到变幅杆与外界的装配问题, 在节点处增加了一厚度为4 mm、外径为62 mm的法兰盘,对其与柱形换能器连接成的整体进行实验研究,两者通过螺栓连接,如图5所示,其中换能器的理论设计频率为20 kHz,理论放大倍数为7.92。

图5 连接后的换能器与变幅杆
4.1性能测试
为验证设计结果,通过实验测量其谐振频率、阻抗特性、放大系数等参数。利用PV70A阻抗分析仪测试整体的谐振频率,测试结果如图6所示。
图中F即谐振频率。实验测得的谐振频率为19.874 kHz,与理想值20 kHz的相对偏差为0.63%,实验频率与设计频率非常接近。分析偏差产生的原因,一方面可能是加工误差和材料参数偏差,另一方面可能是理论设计时未考虑法兰的影响。图形显示的导纳圆是个规则的单圆,且对数坐标图中只有一对极小值和极大值,阻抗测试结果表明,该变幅杆工作性能良好。
利用基恩士的超高速/高精度CMOS激光位移传感器LK-G5000对变幅杆输出端振幅进行测试。在功率为96 W、振幅为60%时,测试结果如图7所示。从图中曲线可以看出,超声波变幅杆做简谐振动,振幅呈周期性变化,且振幅分布十分稳定,变幅杆输出端振幅为18 μm,此功率下换能器的输出振幅为2.35 μm。由此可得,变幅杆的实际放大系数为7.66,与优化前相比提高了29%,与仿真结果的相对偏差为3.2%。偏差产生的原因,一方面是加工误差,另一方面是由于换能器和变幅杆连接时采用手动装配,预紧力不足影响了超声波的传播质量。
4.2试切实验
为了解所设计变幅杆的超声切割效果,利用优化设计所得到的贝塞尔曲线形超声波变幅杆对NOMEX蜂窝复合材料进行超声切割加工实验,实验装置如图8所示。切割加工后的蜂窝复合材料表面如图9所示,切割表面没有明显的毛刺,未出现开裂、压塌等缺陷,满足蜂窝复合材料零件的加工要求,而且加工过程中变幅杆表面温升较小。

图6 谐振频率测试结果界面图
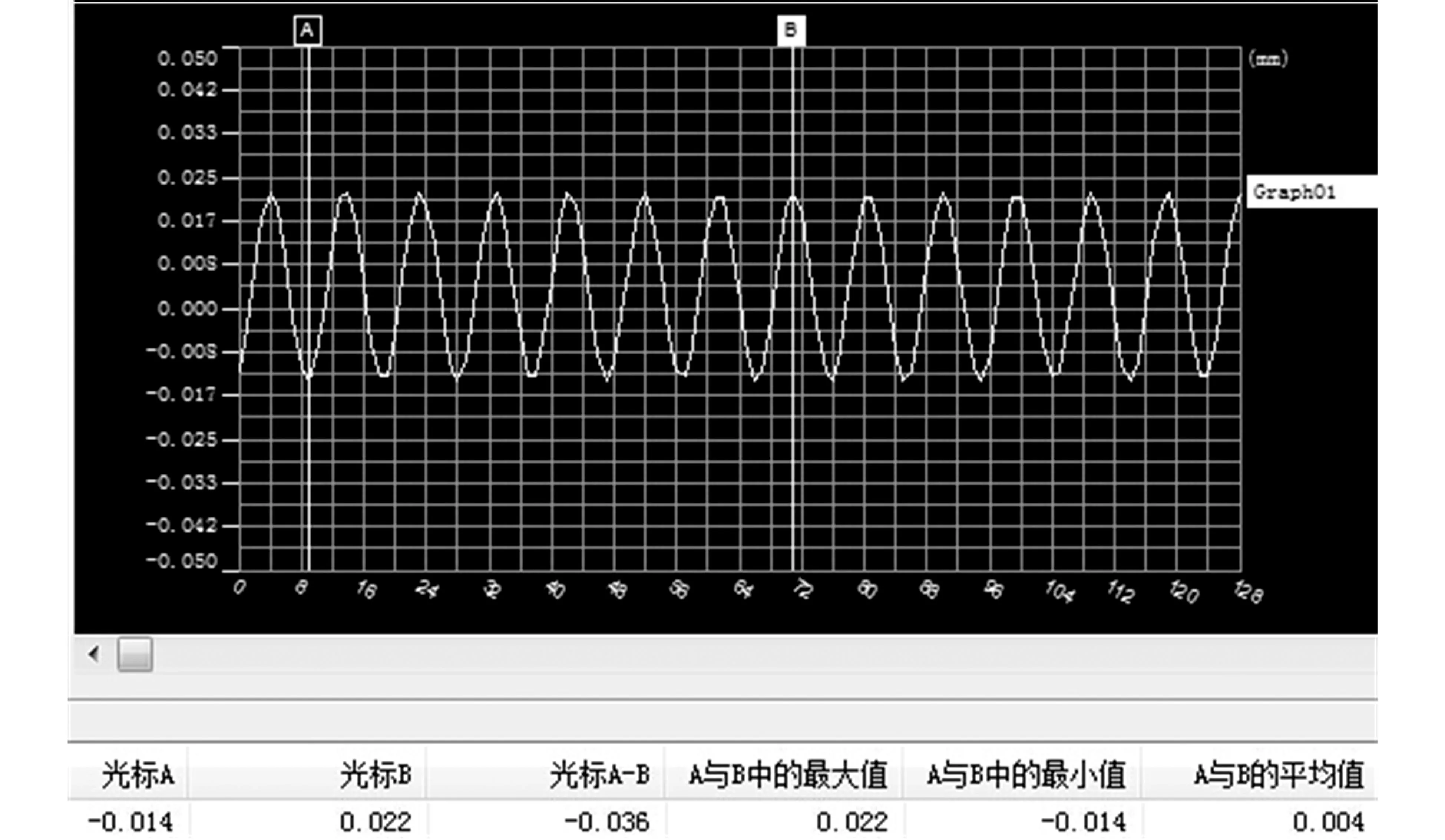
图7 变幅杆输出端振幅测试结果界面图

图8 试切装置
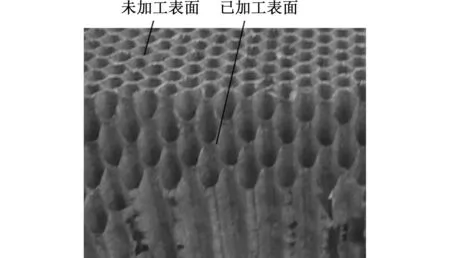
图9 切割后蜂窝复合材料表面
试切实验结果表明:工具振幅满足加工要求,工艺效果好,切割过程容易实现,加工后的蜂窝复合材料的表面质量较好。
5结束语
本文建立了贝塞尔曲线形变幅杆的多目标优化数学模型,并将多目标遗传算法应用于该变幅杆的结构优化设计中,通过对变幅杆有限元参数化建模和分析文件的调用,方便地实现了谐振频率最接近工作频率和放大系数最大两目标参数的优化。利用该优化设计方法,获得了目标空间内的Pareto最优解,得到变幅杆结构参数的最优组合,有效克服了超声变幅杆设计时人工经验依赖性强的缺陷。通过实验验证了该方法的正确性和有效性。本文的研究方法可以方便地实现多方案设计。
参考文献:
[1]GuzzoPL,ShinoharaAH.AComparativeStudyonUltrasonicMachiningofHardandBrittleMaterials[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering, 2004, 26(1):56-61.
[2]沙金,周胜利,姚志远. 超声切割刀动力学分析和结构优化设计[J]. 中国机械工程, 2013,24(12): 1631-1635.
ShaJin,ZhouShengli,YaoZhiyuan.DynamicsAnalysisandStructuralOptimizationDesignofanUltrasonicCutter[J].ChinaMechanicalEngineering, 2013,24(12): 1631-1635.
[3]谨亚辉. 超声波变幅杆优化设计及加工机理试验研究[D]. 太原:太原理工大学, 2010.
[4]陶晓明,刘泽祥,康敏. 超声电解复合加工装置的振动系统优化设计[J]. 中国机械工程,2014,25(6):761-765.
TaoXiaoming,LiuZexiang,KangMin.OptimumDesignofUltrasonicVibrationSystemofCombinedUltrasonicandElectrochemicalDevice[J].ChinaMechanicalEngineering, 2014,25(6): 761-765.
[5]NadM.UltrasonicHornDesignforUltrasonicMachiningTechnologies[J].AppliedandComputationalMechanics, 2010, 4(1):79-88.
[6]宋峥. 超声振动切削系统的建立及变幅杆性能的仿真研究[D]. 哈尔滨:哈尔滨工业大学, 2006.
[7]AminSG,AhmedMHM,YoussefHA.Computer-aidedDesignofAcousticHornsforUltrasonicUsingFinite-elementAnalysis[J].JournalofMaterialsProcessingTechnology, 1995,55(3/4):254-260.
[8]NadM,CicmancovaL.TheEffectoftheShapeParametersonModalPropertiesofUltrasonicHornDesignforUltrasonicAssistedMachining[C]//ProceedingsoftheInternationalConferenceofDAAAMBaltic‘IndustrialEngineering’. 2012: 57-62.
[9]陈彬,张贤明,牟瑛,等. 基于NSGA-Ⅱ的多目标遗传算法通用涡旋盘的优化设计[J]. 中国机械工程. 2012,23(13): 1598-1602.
ChenBin,ZhangXianming,MuYing,etal.OptimizationDesignofGeneralScrollBasedonMulti-objectiveGeneticAlgorithmofNSGA-Ⅱ[J].ChinaMechanicalEngineering, 2012,23(13):1598-1602.
[10]DebK,PratapA,AgarwalS,etal.AFastandElitistMultiobjectiveGeneticAlgorithm:NSGA-II[J].IEEETransactionsonEvolutionaryComputation, 2002, 6(2): 182-197.
(编辑袁兴玲)
收稿日期:2015-08-25
基金项目:国家自然科学基金资助项目(51475130);国防科工局重大专项(A3920133001)
中图分类号:TH113.1
DOI:10.3969/j.issn.1004-132X.2016.13.003
作者简介:纪华伟,男,1976年生。杭州电子科技大学机械工程学院副教授、博士。主要研究方向为精密定位与微纳驱动、特种加工技术。赵双双,女,1989年生。杭州电子科技大学机械工程学院硕士研究生。胡小平,女,1970年生。杭州电子科技大学机械工程学院教授、博士。
Optimal Design Method for Bezier Ultrasonic Horn Based on Multi-objective Genetic Algorithm
Ji HuaweiZhao ShuangshuangHu Xiaoping
Hangzhou Dianzi University,Hangzhou,310018
Abstract:In order to design high performance ultrasonic horn that was used to manufacture honeycomb composite material, a new approach was put forward to design ultrasonic horn based on multi-objective genetic algorithm. By using structural parameters of the ultrasonic horn as design variables, the resonant frequency and amplification factor as optimization goals, an optimization mathematical model of the Bezier ultrasonic horn was established. To get the parameters for calculating fitness function, a finite model and dynamics analysis of ultrasonic horn were carried out by calling ANSYS software from genetic algorithms, and the Pareto-optimal solution set was obtained by genetic algorithm, then, the most suitable parameters of ultrasonic horn were chosen for horn design. At last, the performance test of ultrasonic horn and trial cut experiment of honeycomb composite material show that amplification factor of optimized ultrasonic horn is as 7.66, it is 29 percent higher, and the working frequency is closer to design frequency than un-optimized ultrasonic horn. Simulation and experimental results confirm the reliability and validity of the proposed design method.
Key words:Bezier ultrasonic horn; multi-objective optimization; genetic algorithm; honeycomb composite material

