再入返回离轨时机及制动策略

王献忠 汤敏兰 张丽敏 刘 禹

1. 上海市空间智能控制技术重点实验室, 上海 200233 2. 上海航天控制技术研究所, 上海 200233



再入返回离轨时机及制动策略

王献忠1,2汤敏兰1,2张丽敏1,2刘 禹1,2

1. 上海市空间智能控制技术重点实验室, 上海 200233 2. 上海航天控制技术研究所, 上海 200233

水平定点着落再入返回飞行器对再入角、再入点至着落点的纵程和横程有较严格的要求，飞行器侧向机动能力决定最大横程误差和可返回时机。为设计满足上述要求的飞行轨迹，提出了一种离轨时机及制动策略计算方法。根据再入轨迹分析和着落点经纬度，估计再入轨道最优升交点地理经度；利用横程误差计算返回圈升交点地理经度范围，并推算升交点地理经度优选离轨时机；通过地固系下再入角估计惯性系下速度倾角，由再入点经纬高和速度倾角推算离轨制动时刻及速度增量，由迭代修正生成离轨制动策略，并经算例仿真验证。 关键词 再入飞行器；制动；离轨；再入轨迹；再入返回；纵程；横程；再入角

载人飞船等再入返回器在陆地或海上垂直着落，X-37B等再入返回飞行器可以在机场定点水平着落，水平定点着落相对垂直着落对再入返回飞行器再入角、再入点至着落点纵程和横程有更严格的要求。再入返回飞行器再入角直接影响再入过程气动加热，再入点至着落点纵程影响末端能量管理及能否无动力到达机场，侧向机动能力决定最大横程和可返回圈次。

再入返回飞行器离轨再入及着落过程如图1所示，再入返回飞行器离轨制动研究内容主要包括再入轨迹参数、离轨时机和控制策略。

图1 再入返回飞行器离轨再入及着落过程

再入轨迹参数包括过渡轨道、再入角、再入点至着落点横程和纵程、再入走廓等，这些参数需要结合再入返回飞行器升阻比、水平/垂直着落等要求确定。文献[1]针对再入角和再入点位置给定条件下的空天再入飞行器过渡段轨道设计问题，推导了由给定再入角解析计算初始航迹角的公式，进而可用初始航迹角由极坐标系下的转移轨道速度计算公式直接求出所需的离轨制动脉冲；并以初始轨道飞行弧段对应的地心角为迭代变量，采用黄金分割法迭代求解出转移时间最短和燃料消耗最小过渡轨道对应的制动点位置。文献[2]对其最佳离轨制动、离轨机动和大气入口点再入角的确定进行了分析，并分析了切线制动和非切线制动的再入轨道特点，以及再入角的最佳控制范围。文献[3]采用遗传算法与经典优化方法相结合的组合优化策略求解天基对地打击武器的最优过渡轨道，克服传统优化方法对初值的敏感问题。文献[4]采用双倾角条带覆盖方式解决了传统天基对地打击部署方法的不均匀问题，在满足全球覆盖性的同时提高了对重点区域的覆盖重数。文献[5]提出了一种基于割线法的标准轨迹快速生成方法，在已知再入过程约束和端点约束的前提下，使可重复使用飞行器满足制定航程和终端点速度要求。

离轨时机需要在再入角、再入点至着落点横程等约束下，分析再入返回可行性及回归性，并选择合适的返回圈次，文献[6]针对离轨段轨道设计中飞行器需周期性满足离轨点要求的问题，提出了一种具有一定回归周期的回归轨道设计方法。

控制策略需要确定离轨制动点纬度幅角、离轨制动速度方向及速度增量、再入轨迹控制等，文献[7]研究了飞船离轨返回制动段的制导方法, 提出了一种基于再入点速度倾角偏差的制动发动机关机方法，比按标准关机时间关机和按标准关机速度关机的纵横程偏差小。文献[8]利用hp自适应伪谱法，以燃料最省为优化指标，采用可调推力制动时，飞行器过渡段飞行时间更长，燃料消耗相对较小；在时间最短指标要求下，可调推力制动虽消耗大量燃料，但能大大缩短过渡段飞行时间，有利于航天器在执行紧急任务时的快速返回。文献[9]对航天器在有限推力作用下的“推-滑-推- 滑”离轨轨道制导问题进行了研究，得到了首次制动时推力方向始终与速度方向相反，二次制动根据制导方程进行导引的轨道形式，解决了单次“推-滑”无法实现的离轨制导问题。文献[10]针对使用固体火箭发动机的航天器离轨制动问题，提出了将速度增益制导与随机剩余燃料耗散相结合的混合制导方法，通过攻角方向切换来控制随机剩余燃料对离轨制动的影响。文献[11]提出了一种最优预测校正制导方法，将制导问题转换为不需要积分弹道的最优规划问题，利用Gauss伪谱法设计了航路点间分段优化的伪谱自适应鲁棒再入制导律，提高再入制导的适应性和鲁棒性。

本文重点研究离轨时机和离轨控制策略，首先基于再入轨迹分析和着落点经纬度，估计再入轨道最优升交点地理经度；然后基于横程误差计算返回圈升交点地理经度范围，并通过推算升交点地理经度优选离轨时机；最后基于地固系下再入角估计惯性系下速度倾角，由再入点经纬高和速度倾角推算离轨制动时刻及速度增量，并通过迭代修正生成离轨制动策略。

1 估计再入轨道升交点地理经度

1.1 再入轨迹分析及纵横程计算

以升轨再入返回为例，可能再入轨迹如图2所示，再入可能轨迹可能有2条，即轨迹1：B1C，轨迹:2：B2C。B1C基本沿轨道面再入，B2C在着落场纬度附近基本沿纬度圈再入。

图2 升轨再入返回可能轨迹示意图

以再入轨迹B1C为例进行纵横程计算，如图3所示，其中dS为纵程距离，dY为横程距离。(Lf,λf)为着落场经纬度，(Lr,λr)为再入点经纬度，ψ为再入点方位角，ψ0为机场相对于再入点的方位角，dψ为再入点方位角相对于着落场方位角的偏差，u为着落场至再入点大圆弧距，dL为着落场与再入点经度差。

图3 升轨再入返回纵程和横程

令λfs=π/2-λf为着落场余纬，λrs=π/2-λr为再入点余纬，由球面三角形AB1C求得：

cosu=cosλfs·cosλrs+sinλfs·sinλrs·cosdL

(1)

sinψ0=sinλfs·sindL/sinu

(2)

cosψ0=

(cosλfs·sinλrs-sinλfs·cosλrs·cosdL)/sinu

(3)

由式(2)和(3)求得：

ψ0=

(4)

dψ=ψ-ψ0

(5)

由球面直角三角形B1CD求得纵程dS如下：

(6)

由球面直角三角形B1CD得：

sindY=sinu·sindψ

(7)

cosdY=cosu/cosdS

(8)

求得横程dY如下：

(9)

其中，顺着飞行方向左侧横程为负，右侧横程为正。

1.2 最优升交点地理经度估算

横程为0的再入轨道升交点为最优升交点，对于再入轨迹1：B1C，如图3所示，着落场相对最优升交点经度差为dL1，由直角球面三角形CEF求得dL1：

(10)

其中，i为再入轨道倾角。

求得最优升交点地理经度Ωe1：

Ωe1=Lf-dL1

(11)

其中，Lf为着落场地理经度。

对于再入轨迹:2：B2C，可以根据纵程近似求取最佳升交点地理经度，设再入轨迹沿落场纬度圈飞行，如图2中的虚线所示，再入点B2可近似为B3，B3相对着落场的经度差为dL2：

(12)

其中，dS0为纵程标称值，λf为着落场地理纬度。

将B3看作着落场，类似再入轨迹B1C，近似求得再入轨迹B2C的最优升交点地理经度Ωe2：

Ωe2≈Ωe1-dL2=Lf-dL1-dL2

(13)

2 离轨时机优选

2.1 基于最大横程估计升交点地理经度范围

设再入返回飞行器横程最大机动能力为dYm，如图4所示，由球面直角三角形EDF可求得升交点地理经度范围dLe：

dLe=arctan(tan(dYm)·sinir)

(14)

其中，ir为再入轨道倾角。

考虑最优升交点地理经度估算误差，实际应用中dLe要适度放宽。

图4 升交点地理经度范围

2.2 升交点地理经度推算及离轨时机优选

(15)

(16)

其中，ωe为地球自转角速率。

设当前轨道纬度幅角为u，求得当前轨道位置第1次到达升交点时间dt1：

(17)

第1次到达升交点后再过N轨，即到达N+1个升交点时间dt：

(18)

设当前轨道位置地理经度为Le 0，则到达N+1个升交点位置地理经度Le：

(19)

对于图2中再入轨迹B1C，可离轨圈次判别条件如下：

(20)

对于图2中再入轨迹B2C，可离轨圈次判别条件如下：

(21)

从当前轨道位置到未来N+1个升交点之间，优选升交点地理经度相对最优升交点地理经度偏差较小的圈次进行离轨制动，再入返回横程较小。

3 离轨制动策略生成及迭代修正

3.1 基于地固系再入角估算惯性系速度倾角

再入返回考虑气动加热特性，将标称再入角定义在地固系，而轨道推算在惯性系，需要将地固系下定义的再入角转换成惯性系下的速度倾角。

设离轨制动后再入轨道半长轴为ar，再入点高度为hr，根据活力公式求得再入点相对惯性系速度vri：

(22)

其中，μ为地球引力常数。

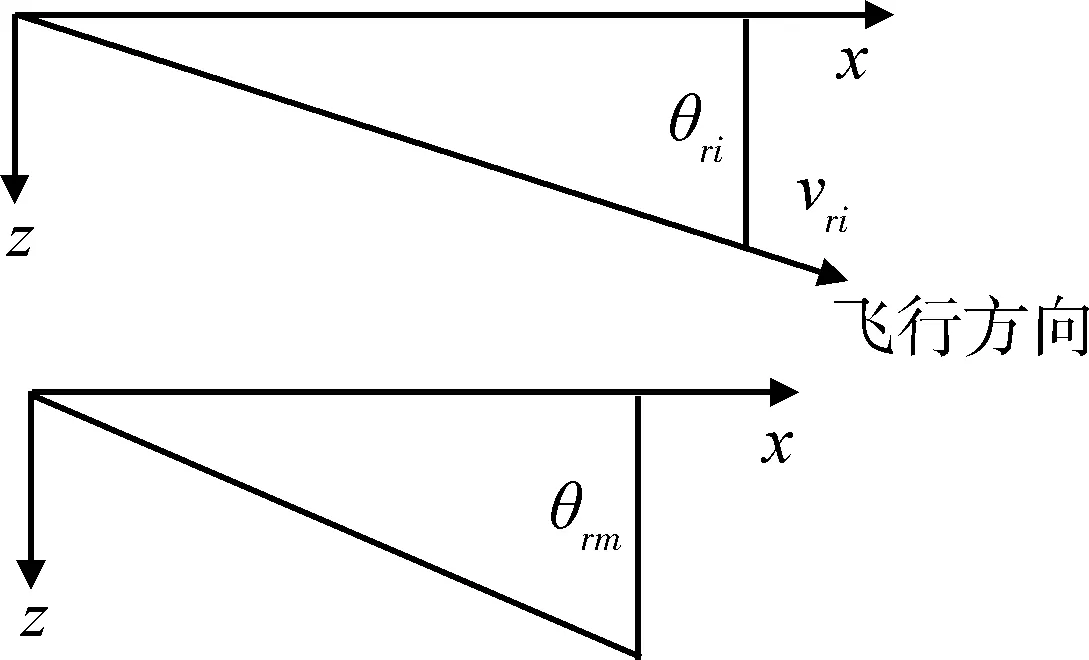
图5 惯性系速度倾角和地固系再入角

如图5，设惯性系下再入点标称速度倾角为θri，求得轨道面内水平方向速度vxi和地心方向速度vzi：

vxi=vri·cosθri

(23)

vzi=vri·sinθri

(24)

由式(24)求得地固系下轨道面内水平方向速度vze：

vxe=vxi-ve=vri·cosθri-ve

(25)

其中，ve为地速在轨道面内水平方向的分量，可以根据再入点纬度和轨迹方位角估算。

如图5，设地固系下标称再入角为θre，由式(25)求得地心方向速度vze：

vze=vxe·tanθre=(vri·cosθri-ve)·tanθre

(26)

惯性系和地固系下地心方向速度相等，即vzi=vze；再入角较小，cosθri≈cosθre≈1，由式(24)和(26)求得θri：

(27)

定点水平着落再入返回速度倾角一般在-1°左右，根据式(27)估算惯性系速度倾角与地固系再入角偏差约0.005°。

3.2 再入返回轨道半长轴及偏心率计算

再入轨道速度倾角θi可以根据地心距r求得：

(28)

其中，ar为再入轨道半长轴，er为再入轨道偏心率。

再入轨道离轨制动点处速度倾角θbi：

(29)

其中，rb为离轨制动点处地心距。

再入点处速度倾角θri：

(30)

其中，rr=Re+hr为再入点处地心距。

求得再入轨道半长轴ar：

(31)

由活力公式求得离轨制动后速度vb：

(32)

再入轨道半通径pr：

(33)

其中，hr=rb·vb为再入轨道动量矩。

求得再入轨道偏心率er：

(34)

3.3 离轨制动速度增量及制动点纬度幅角推算

设离轨制动前速度为v0：

(35)

其中，a0为离轨制动前轨道半长轴。

采用省推进剂的水平面内反推制动，求得离轨制动速度增量Δv：

Δv=(v0-vb)·cosθbi

(36)

再入轨道离轨制动点处真近点角fb：

(37)

再入点处真近点角fr：

(38)

离轨制动点至再入点真近点角差dfrb：

dfrb=fr-fb

(39)

其中，dfrb∈[0,2π)

根据着落点纬度λf及轨道倾角ir，可求得再入轨道在着落点处纬度幅角uf：

(40)

考虑优选再入时机后方位角偏差为小量，即dψ≈0，由式(6)及纵程标称值dS0，可求得再入点相对着落点纬度幅角差dufr：

dufr=uf-ur≈dS0

(41)

由式(40)可求得再入点处纬度幅角ur：

(42)

由式(39)和(41)可估计离轨制动点处纬度幅角ub：

ub=ur-durb≈ur-dfrb

(43)

3.4 推算初始化及迭代修正

式(31)中rb初值可设为离轨制动前轨道半长轴a0，θb可设为0，根据式(43)估计出离轨制动点处纬度幅角ub，并进一步迭代修正rb和θb。

根据离轨制动策略中的离轨制动点纬度幅角和制动速度增量计算再入角及纵横程，再基于纵程及再入角偏差迭代修正离轨制动纬度幅角和制动速度增量，优化离轨制动策略。

4 算例仿真验证

设2008年11月7日北京时间16：00：00飞行器离轨制动前轨道高度400km，偏心率为0.003，倾角48°，近地点幅角为0，升交点赤经328.72°，平近点角161.18°。

再入点高度为120km，再入点地固系速度倾角标称值为-1.1°，纵程标称值为8000km，最大横程600km。3天内离轨时机及制动策略如表1所示，3天内有5次离轨机会，其中轨迹1有3次，轨迹2有2次，轨迹2所需速度增量大于轨迹1，第2天第35轨离轨横程误差最小。

表1 3天内离轨时机及制动策略

5 结束语

基于着落点经纬度、再入点至着落点纵程要求和再入飞行器机动能力决定的最大横程约束，计算了两种再入返回轨迹再入点经度和纬度，并估算了当前轨道可离轨时机。结合再入返回飞行器对再入点高度和再入角的要求，以及离轨制动前轨道，推算了离轨制动后过渡轨道半长轴、偏心率和离轨制动时的纬度幅角及速度增量，通过迭代修正生成的离轨制动策略，并经算例仿真验证。

[1] 郭付明,高晓光,端军红. 空天再入飞行器最优过渡段轨道设计方法研究[J]. 航天控制，2014，32(4)：69-90. (Guo Fuming, Gao Xiaoguang, Duan Junhong. Research on Optimal Transition Trajectory Planning for Reentry Vehicle [J]. Aerospace Control, 2014, 32(4):69-90.)

[2] 陈洪波, 杨涤. 升力式再入飞行器离轨制动研究[J]. 飞行力学，2006，24(2)：35-39. (Chen Hongbo, Yang Di. Research on Lift Reentry Vehicle Braking on Orbit [J]. Flight Dynamics, 2006, 24(2):35-39.)

[3] 袁宴波,李东伟. 天基对地打击武器最优过渡轨道研究[J]. 科学技术与工程，2009，9(6)：1146-1149. (Yuan Yanbo, Li Dongwei. A Research on the Optimal Transfer Orbit Space-based Strike Weapon [J]. Science Technology and Engineering, 2009, 9(6):1146-1149.)

[4] 姚玮,罗建军,方群. 一种新的升力式再入投送系统轨道部署方法[J]. 宇航学报, 2014,35(9):992-999.(Yao Wei, Luo Jianjun, Fang Qun. A Novel Orbit Deployment Method for Lifting Reentry Delivery System[J]. Journal of Astronautics, 2014, 35(9):992-999.)

[5] 沈振,胡钰,任章,宋剑爽. 一种新型RLV再入轨迹在线规划方法[J]. 宇航学报, 2011,32(8):1670-1675.(Shen Zhen, Hu Yu, Ren Zhang, Song Jianshuang. A New On-line Planning Method for RLV Reentry Trajectory Design[J]. Journal of Astronautics,2011,32(8): 1670-1675.)

[6] 汤敏兰,刘赟. 离轨段回归轨道设计[J]. 航天控制，2013，31(6)：62-65,70. (Tang Minlan, Liu Yun. The Design of Recursive Orbit During Deorbit [J]. Aerospace Control, 2013, 31(6):62-65,70.)

[7] 陈克俊. 飞船返回再入制导方法研究[J]. 国防科技大学学报，1997，19(6)：31-35. (Chen Kejun. An Approach to Spacecraft Returning Reentry Guidance [J]. Journal of National University of Defense Technology, 1997, 19(6):31-35.)

[8] 冯必鸣,聂万胜,郑刚. 基于hp自适应伪谱法的可调推力最优离轨研究[J]. 飞行力学，2013，31(4)：354-358,362.(Feng Biming, Nie Wangsheng, Zhen Gang. Optimal Deorbit Research of Spacecraft with Variable Thrust Based on Hp-Adaptive Pseudo Spectral Method [J]. Flight Dynamics，2013, 31(4):354-358, 362.)

[9] 邹毅,张洪波,汤国建. 基于能量与动量矩指标的两次“推-滑”离轨制导方法[J]. 国防科技大学学报，2014，36(1)：46-51.(Zou Yi, Zhang Hongbo, Tang Guojian. A Burn-coast-burn-coast Deorbit Guidance Approach Based on Energy And Angular Momentum Indices [J]. Journal of National University of Defense Technology，2014, 36(1):46-51.)

[10] 邹毅,张洪波,汤国建，等. RLV 离轨制动耗尽关机制导方法研究[J]. 固体火箭技术，2013，36(5)：575-579.(Zou Yi, Zhang Hongbo, Tang Guojian, et al. Research on Depleted Shutdown Guidance Approach of Reusable Launch Vehicle Deorbit [J]. Journal of Solid Rocket Technology, 2013, 36(5):575-579.)

[11] 水尊师,周军,葛致磊. 基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J]. 宇航学报, 2011,32(6):1249-1255.(Shui Zunshi, Zhou Jun, Ge Zhilei. On-Line Predictor-Corrector Reentry Guidance Law Based on Gauss Pseudospectral Method[J]. Journal of Astronautics, 2011, 32(6):1249-1255.)

[12] 王希季. 航天器进入与返回技术[M]. 北京：中国宇航出版社，1991.(Wang Xiji. Spacecraft Entering and Returning Technology[M]. Beijing: China Aerospace Press，1991.)

Deorbit Times and Braking Strategy for Reentry Vehicle

Wang Xianzhong1,2, Tang Minlan1,2, Zhang Limin1,2，Liu Yu1,2

1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 200233, China 2. Shanghai Aerospace Control Technology Institute, Shanghai 200233, China

Thefixed-pointhorizontallandingreentryvehicleshavemorestringentrequirementsofthereentryangle,longitudinalrangeandcrossrangefromthereentrypointtothelandingpoint.Thelateralmaneuveringcapabilityofreentryvehicledeterminesthemaximumcrossrangeerrorandthetimetoreturn.Thedeorbittimesandbrakingstrategyisproposedforthistrajectorydesign.Theoptimallongitudeofascendingnodeofreentryorbitisestimated,whichisbasedontheanalysisofreentrytrajectoryandthelatitudeandlongitudeofthelandingpoint.Preferdeorbittimeisdeterminedbythecalculationofgeographicallongitudeandthelongituderangeofascendingnodeofreentrytrajectorybasedoncrossrangeerror.Thevelocityinclinationangleininertialsystemisestimated,whichisbasedonthereentryangleinthegroundsystem.Thebrakingmomentandvelocityincrementareobtainedbyapplyingthereentrypoint’sgeographicallatitude,longitude,heightandreentryangle.Thedeorbitstrategyisgeneratedbytheiterativecorrection.Thesimulationresultvalidatesthedeorbitstrategybycalculationexample.

Reentryvehicle;Brake;Deorbit;Reentrytrajectory;Reentry;Longitudinalrange;Crossrange;Reentryangle

2016-03-10

王献忠(1971-)，男，江苏太仓人，博士，研究员，主要研究方向为飞行器GNC系统研究与设计；汤敏兰(1987-)，女，江苏常熟人，硕士，工程师，主要研究方向为飞行器轨道控制研究与设计；张丽敏(1981-)，女，河南新乡人，硕士，高级工程师，主要研究方向为飞行器自主导航算法研究和设计；刘 禹(1992-)，男，江苏江都人，硕士研究生，主要研究方向为飞行器自主导航。

V448.2

A

1006-3242(2016)04-0053-06