基于Maxima软件的高等数学可视化演示

陈　华，桑兆阳，李维国

(中国石油大学(华东) 理学院，山东　青岛　266580)



基于Maxima软件的高等数学可视化演示

陈华，桑兆阳，李维国

(中国石油大学(华东) 理学院，山东青岛266580)

摘要通过使用开源软件Maxima，以可视化的方式对高等数学中极限、微积分、常微分方程、级数等部分内容进行了演示。将抽象的数学概念、繁杂的计算，通过Maxima软件以界面操作的方式表现出来，在一定程度上起到激发学生学习兴趣、促进知识理解、增强教学效果的作用。

关键词Maxima；高等数学；数学实验；可视化

数学实验是以数学理论知识作为原理，以软件编程、图形演示和数值计算等为实验内容，以实际生活问题和数学教材为实验对象，以计算机作为工具，以分析建模、模拟仿真、软件求解和总结推广为主要实验方法，并以实验报告为最终体现形式的实践活动[1]。大学数学实验作为一门新兴的数学课程在近十年来取得了迅速的发展，数学实验对数学教学改革的促进作用已得到了广泛共识[2-6]。数学实验的软件载体基本上是Matlab、Mathematica和Maple等商业化数学软件，这些软件无论在功能还是在性能上都能满足高等数学实验的要求，但这些大而全的商业软件也存在一些问题，主要有：1)价格不菲，购置其中任何一款数学软件都需要至少几十万元的投入，这对于资金紧张的学校难以购买这些商业软件；2)所占硬盘空间大，这些软件动辄几千兆的安装，使机房的软件安装与维护变得非常麻烦。而开源软件Maxima则不存在这些问题，且能够完成高等数学中各项实验。虽然Maxima几乎在中国大陆看不到踪影，但在美国、中国台湾等地使用较为普遍。

1Maxima软件简介

Maxima软件的前身是DOE-Macsyma。DOE-Macsyma是由麻省理工学院(MIT)在美国能源部的支持下于20世纪60年代末创造的一种CAS，它是用LISP实现的。Macsyma在当时是非常创新的软件，现在流行的商业计算机代数系统软件Maple及Mathematica，都是受到Macsyma的启发而设计出来的。MIT在1982年的时候决定把Macsyma变成一个关闭源码的程序，Macsyma 走上商业化的道路，于是产生了很多Macsyma的分支。

自1982年开始，Bill Schelter教授开始开发一个开放源码版的Macsyma，他把这个软件叫作Maxima。1998年，Maxima得到公开发行的许可，这已是Bill Schelter教授努力了16年之后的事。Bill Schelter教授在2001年去世，Macsyma已正式成为合法开放源码软件，因此陆续有支持开放源码的程序设计师、学者投入Maxima的开发工作。在Maxima的官方网站上有不同版本的 Maxima供各平台实用，当前最新版为2015年4月发布的Maxima-5.36.0版，大小仅为51.1 MB。下载安装后即可使用，该软件若安装在中文版操作系统下，则界面为中文界面，图1为Maxima软件主界面。

图1　Maxima软件主界面

Maxima软件界面中有文件、编辑、单元、Maxima、方程、代数、微积分、化简、绘图、数值和帮助等菜单。另外，还有大量的程序包供调用。而高等数学的主要内容涉及极限、微积分、常微分方程、级数等内容[7-8]，下面从这4个方面介绍怎样使用Maxima进行数学实验。

2高等数学实验

2.1极限

点击“微积分”菜单，找到子菜单“求极限”，出现极限对话框，根据问题要求输入即可。

进入极限对话框，输入表达式(x＾2+2)＾(1/2)/(3*x-6)，点inf(单击右侧“特殊”选择无穷大)，最后点击确认按钮，在主界面中得到极限函数表达式和计算结果：

limit((x＾2+2)＾(1/2)/(3*x-6),x,inf);

1/3

进入极限对话框，输入表达式lg(x)/x，点0，方向选择“向右”，最后点击确认按钮，在主界面中得到极限函数表达式和计算结果：

limit(lg(x)/x,x,0,plus);

-∞

该例子比前两个例子要复杂，不能直接使用极限对话框。首先加载差分方程函数solve_rec，使用solve_rec求解出an；然后再用limit求极限。在主界面中输入命令：

load(solve_rec);

solve_rec(a[n+1]=a[n]/(1+a[n]),a[n],a[1]=1);

每步输出结果如图2所示。

图2　例3输出结果

2.2微积分

进行微分计算，点击“微积分”菜单，找到子菜单“微分”，出现微分对话框，根据问题要求输入即可。

例4求函数exsin(x)的2阶导数。

进入微分对话框，输入表达式e＾x*sin(x)、变量x，微分次数设为2，最后点击确认按钮，在主界面中得到导数表达式和计算结果：

diff(e＾x*sin(x),x,2);

2excos(x)

例5求函数xf(x)的1阶导数。

进入微分对话框，输入表达式x*f(x)、变量x，其他为默认，点击确认按钮，在主界面中得到导数表达式和计算结果：

diff(x*f(x),x,1);

对于积分计算，点击“微积分”菜单，找到子菜单“积分”，出现积分对话框，根据问题要求输入即可。

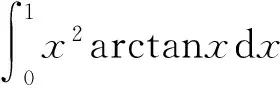
先求不定积分，进入积分对话框，输入表达式x＾2*atan(x)，其他为默认，点击确认按钮，在主界面中得到导数表达式和计算结果：

integrate(x＾2*atan(x),x);

然后求定积分，进入积分对话框，输入表达式x＾2*atan(x)，选中定积分，其他为默认，点击确认按钮，在主界面中得到导数表达式和计算结果：

integrate(x＾2*atan(x),x,0,1);

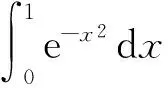
其中，erf是误差函数[9]，它不是初等函数。改为求数值积分。进入积分对话框，输入表达式exp(-x＾2)，选中定积分后，选择数值积分，其他为默认，点击确认按钮，在主界面中得到导数表达式和计算结果：

quad_qags(exp(-x＾2),x,0,1);

0.746 824 132 812 427 1

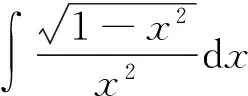
图3　例8换元界面

当然，如果不用界面，直接写3条命令即可完成该项工作，即:

’integrate(sqrt(1-x^2)/x^2,x);

2.3常微分方程

在“方程”菜单中，子菜单中有“求解常微分方程”“一阶常微分方程初始值问题”“二阶常微分方程初始值问题”“边界值问题”和“利用Laplace变换求解常微分方程”，可根据具体问题选择相应子菜单。

点击二阶常微分方程初始值问题子菜单，如图4所示，设置初始条件，点击确认按钮，在主界面中得到方程初值问题的解x=sin(t)+cos(t)。

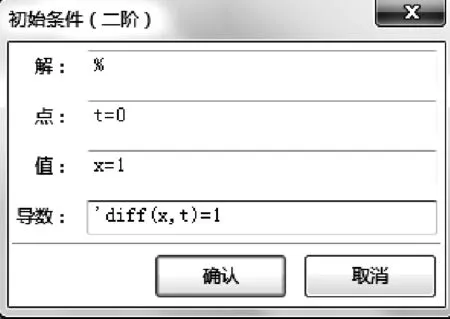
图4　例9求二阶常微分方程界面

图5　例9图解

例10悬链线(catenary)是一种曲线，因其与两端固定的绳子在均匀引力作用下下垂相似而得名。工程中的悬索桥、双曲拱桥、架空电缆、双曲拱坝都用到悬链线的原理。求解并绘制该曲线。

根据受力分析[7,12-13]，可以得到悬链线微分方程和其初始条件：

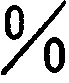
load(mnewton)$

mnewton([cosh(k1)+k2=1,sinh(k2)=0],[k1,k2],[1.0,1.0]);

计算得到k1和k2为0，即悬链线表达式为y=cosh(x)，图形如图6所示。

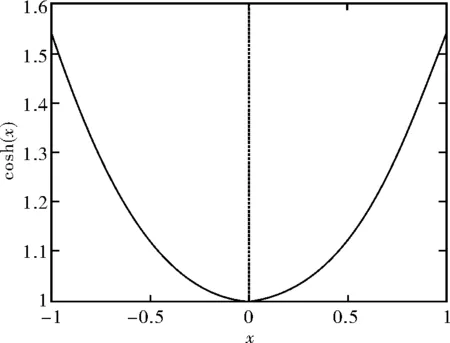
图6　例10图解

2.4级数

点击“微积分”菜单，找到子菜单“取级数”，出现级数对话框，根据问题要求输入即可。

例11将函数y=sinx+cosx展开成x的幂级数。

进入级数对话框，输入表达式sin(x)+cos(x)、变量x、点0，选中幂级数，其他为默认，点击确认按钮，在主界面中得到幂级数表达式为：

进入求和对话框，输入表达式1/k＾2、变量k从1到inf，选中化简，点击确认按钮，在主界面中得到求和表达式和计算结果：

sum(1/k＾2,k,1,inf),simpsum;

π2/6。

3结束语

在高等数学中，使用Maxima软件对极限、微积分、常微分方程、级数等部分内容，进行了可视化实验，其操作非常简单，易于作为课堂中辅助教学和实验工具。Maxima软件虽小，但功能齐全，拥有众多软件包和编程功能，因而其应用不局限于高等数学一门课，还可以用在线性代数、概率统计等其他数学课的实验中。

借助于软件技术辅助高等数学等基础课程，可以将抽象的数学转化为数学实验的形式展现出来，在一定程度上确实起到增强教学效果的作用。但是这些软件技术不可能替代数学的课堂教学，只有将两者有效结合起来，相辅相成，才会取得更好的教学效果。

参 考 文 献

[1]朱永松. 大学数学实验课程研究与实践[J]. 大学教育, 2014(15):109-110.

[2]毛仕理. 加强数学实验教学 培养学生实践能力[J]. 课程教学研究, 2014(5):43-47.

[3]崔艳巧. 开展数学实验教学的实践与体会[J]. 中国现代教育装备, 2014(2):63-64.

[4]杨韧,谢海英. 基于CDIO教育理念的数学实验课程教学改革[J]. 实验室研究与探索, 2012(4):121-123.

[5]谢治州,严忠权,罗晓宾. 数学类专业的数学实验教学研究与实践[J]. 实验室研究与探索, 2012，31(2):109-114,177.

[6]吴晓. 大学数学中的数学实验教学[J]. 大学教育, 2014(5):116-117.

[7]同济大学数学系.高等数学(上册)[M].6版.北京:高等教育出版社,2007.

[8]同济大学数学系.高等数学(下册)[M].6版.北京:高等教育出版社,2007.

[9]王伯年,王宏光. 误差函数计算方法的研究[J]. 上海理工大学学报,2004(6):529-532.

[10]严家良. 推导数学摆的无阻尼自由振动方程的新方法[J]. 广东民族学院学报(自然科学版), 1995(4):10-11.

[11]张全信,燕居让. 二阶非线性阻尼微分方程解的振动性质[J]. 数学杂志, 2007(4):455-460.

[12]胡灵斌,唐军. 悬链线方程的求解及其应用[J]. 船舶, 2004(1):17-20.

[13]王丹,刘家新. 一般状态下悬链线方程的应用[J]. 船海工程, 2007(3):26-28.

Visualization Demo of Higher Mathematics Based on Maxima

CHEN Hua, SANG Zhaoyang, LI Weiguo

(College of Science, China University of Petroleum, Qingdao 266580, China)

AbstractBy using open source software of Maxima, the limit, calculus, ordinary differential equations, and series of higher mathematics are demonstrated by visualization. Using Maxima software, the interface can present abstract mathematical concepts, complex calculations with an intuitive and visual way. It can help make an stimulate students’ learning interests and deepen the understanding of knowledge to improve the teaching effect.

Key wordsMaxima; higher mathematics; mathematics experiment; visualization

收稿日期:2015-04-04；修改日期: 2015-10-14

基金项目：中国石油大学(华东)教改项目(JY-B201455,YJ-B1416)；中国石油大学(华东)实验改革重点资助项目(SY-A201402)。

作者简介：陈华(1972-)，男，博士，副教授，主要从事地球物理测井方法和其他工业应用数学问题方面的研究。

中图分类号TP39;G6420

文献标志码A

doi:10.3969/j.issn.1672-4550.2016.02.015