一类矩阵的三特征对逆二次特征问题* 1

汪淑兰，黄贤通

(赣南师范学院 数学与计算机科学学院，江西 赣州　341000)



一类矩阵的三特征对逆二次特征问题* 1

汪淑兰，黄贤通

(赣南师范学院 数学与计算机科学学院，江西 赣州341000)

摘要：研究基于三特征对的逆二次特征问题，给出问题解存在的条件，并且求出有解存在的条件下解的表达式，给出算例并证明理论的正确性.

关键词：特征值；特征向量； 特征对；逆二次特征问题

二次特征问题，是指已知矩阵三元组(M,C,K)，求数λ和向量x满足Q(λ)x=0，这里Q(λ)=λ2M+λC+K，此时称满足detQ(λ)=0的λ为二次特征值，满足Q(λ)x=0的x称为对应于λ的特征向量，称(λ,x)为特征对.这类问题来源于文献[1]带阻尼的弹簧质点系统(此时,M对应质量矩阵,C对应阻尼阵,K对应刚度矩阵) 和文献[2]二阶四网孔电路系统(此时,M对应电感矩阵,C对应电阻阵,K对应电容矩阵).如图1所示.

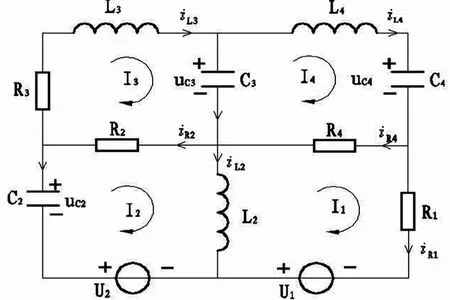
图1

图1中四网孔电路中Ui是电压，Ii是电流，Ri是电阻，Li是电感，Ci是电容.

逆二次特征问题，是指根据矩阵三元组(M,C,K)的部分信息，寻找M、C、K的全部信息，使得具有事先给定的特征值，或具有事先给定的特征对，前者被称为逆二次特征值问题，后者被称为逆二次特征对问题.文献[3-7]中探究了逆二次特征问题，当给定信息不同时， 使得满足给定条件以达到对电路的设计.本文以二阶电路系统中的四网孔电路的设计为背景，研究了三特征对的逆二次特征值问题：

问题P已知矩阵K∈R4×4中的d3，对于给定的特征值λ,μ,γ，以及对应的特征向量x=(x1x2x3x4)′，y=(y1y2y3y4)′，z=(z1z2z3z4)′，求矩阵M、矩阵C以及矩阵K中的d2,d4，使得下面的式子是成立的：Q(λ)x=0，Q(μ)y=0，Q(γ)z=0. 其中

1问题的解

假设x=(x1x2x3x4)′，y=(y1y2y3y4)′，z=(z1z2z3z4)′，对于方程的解相当于联立：

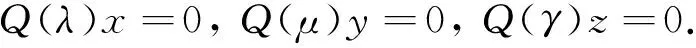
(1)

求解出l2,l3,l4,R1,R2,R3,R4,d2,d4，构造出M、C、K. 可以将问题P的解按下述策略求得：

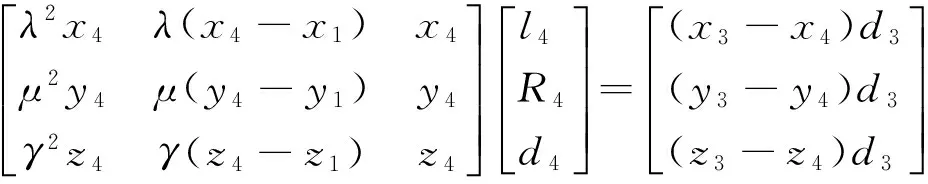
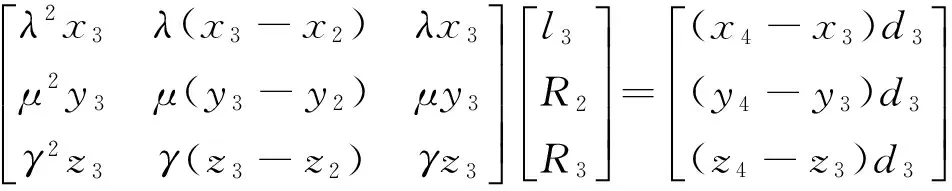
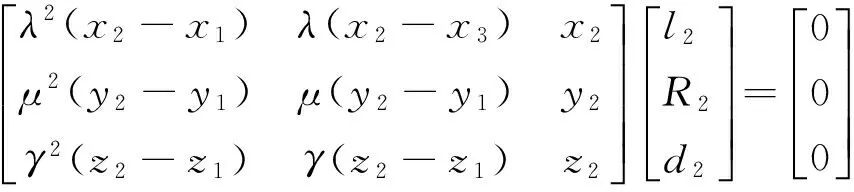
为了求解问题，P-1引入记号:

定理1对于问题P-1有唯一解的条件：当D≠0时，方程有唯一解，且解的表达式为l4=D-1D1，R4=D-1D2，d4=D-1D3.

证明对于问题P-1中矩阵方程有唯一解的条件为系数矩阵是满秩矩阵.因为系数矩阵的行列式值D≠0，系数矩阵必是满秩矩阵,方程必有唯一解.根据克莱默法则得到解的表达式为： l4=D-1D1，R4=D-1D2，d4=D-1D3.

为了求解问题P-2，引入记号:

定理2对于问题P-2有唯一解的条件：当E≠0时，方程有唯一解，且解的表达式为l3=E-1E1，R2=E-1E2，R3=E-1E3.

证明对于问题P-2中矩阵方程有唯一解的条件为系数矩阵是满秩矩阵.因为系数矩阵的行列式值E≠0，系数矩阵必为满秩矩阵，方程也必有唯一解.根据克莱默法则得到解的表达式为：l3=E-1E1，R2=E-1E2，R3=E-1E3. 为了求解问题P-3，引入记号:

定理3对于问题P-3有唯一解的条件是：F≠0,H≠0,且满足F-1F1=H-1H1,F-1F2=H-1H2，且解的表达式为l2=F-1F1，d2=F-1F2.

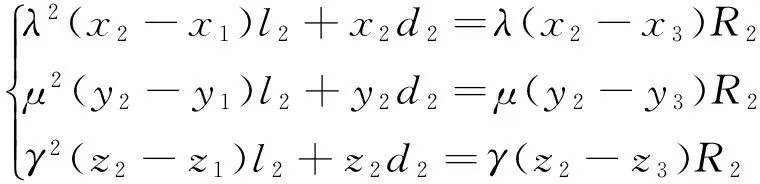
由方程组可以得到：l2=F-1F1，l2=H-1H1，所以只有满足F-1F1=H-1H1，方程组中l2才有解. 另外因为d2=F-1F2，d2=H-1H2,所以只有满足F-1F2=H-1H2，方程组d2才有解. 故得到解的表达式为：l2=F-1F1，d2=F-1F2.

定理4对于问题P-4有唯一解的条件是：M≠0,N≠0,P≠0,M1M-1=N1N-1=P1P-1，解得表达式为：R1=M1M-1.

证明因为R4,l2已求出，所以方程转化为求下列方程组中的未知数R1：

引入记号:

(2)

(3)

(4)

由(2)可知，要使方程有解，系数不能为零，即M≠0，得到R1=M1M-1；

同样由(3)(4)得到N≠0,P≠0，并且得到R1=N1N-1，R1=P1P-1.因为R1是同一个，所以M1M-1=N1N-1=P1P-1.则解得表达式为：R1=M1M-1.

2数值算例

例1已知l2=l3=l4=2，R1=R2=R3=R4=1,d2=d3=d4=1，

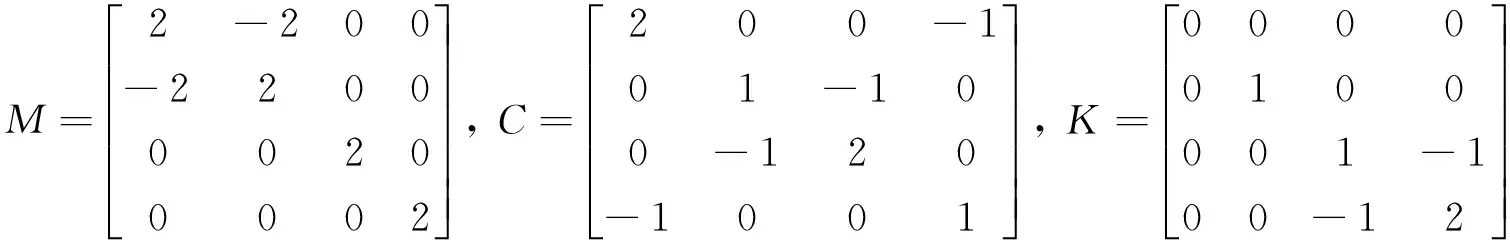
试求三元数组(M,C,K)的特征值和特征向量.

解用MATLAB数学软件计算出(M,C,K)的特征值和特征向量分别如下：

特征值： λ1=0，λ2、3=-0.251 996 16±0.621 419 06i，λ4、5=-0.260 802 89±1.029 598 85i,

λ6、7=-0.403 867 61±0.034 288 73i

特征向量：

例2给出d3=1，三个特征值相应的特征向量：λ=-0.251 996 2+0.621 419 1i, μ=-0.260 802 9+1.029 598 8i,γ=-0.403 867 6+0.034 288 7i.

求l2,l3,l4,R1,R2,R3,R4,d2,d4，从而构造出(M,C,K)，满足下面的形式：

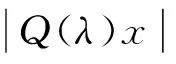
解因为d3=1根据定理并运用MATLAB数学软件计算可得：

通过求解问题P-1：得l4=D-1D1=2.000 000 00-0.000 000 06i,R4=D-1D2=0.999 999 97-0.000 000 00i,d4=D-1D3=1.000 000 00-0.000 000 02i.

通过求解问题P-2：得l3=E-1E1=2.000 000 00-0.000 000 03i,R2=E-1E2=0.999 999 99-0.000 000 02i,R3=E-1E3=1.000 000 00+0.000 000 00i.

通过求解问题P-3：得l2=F-1F1=1.999 999 99-0.000 000 01i,d2=F-1F2=0.999 999 98-0.000 000 03i.

通过求解问题P-4：得R1=M1M-1=0.999 999 93-0.000 000 03i.

参考文献：

[1]王正盛.阻尼弹簧-质点系统中的逆二次特征问题[J].高等学校计算机数学学报，2005,27(3)：217-224.

[2]Moody.T.Chu, GENEH GlouB. Inverse Eigenvalue Problems：Algorithms,and Ap-plications[M].Oxford:Oxford University Press,2005:62-164.

[3]汪淑兰，黄贤通.矩阵二次特征问题在四网孔电路分析中的应用[J].赣南师范学院学报,2014,(6)：7-1.

[4]严深海.双特征值约束下的两类逆二次特征值问题[J].江西理工大学学报,2012,33:88-92.

[5]黄贤通.双复特征值约束下的逆二次特征问题[J].工程数学学报,2015,(32):39-49.

[6]严深海,黄贤通.二阶电路系统设计中的一类逆二次特征问题[J].韶关学院学报(自然科学版),2012,(33)：10-14.

[7]黄贤通,严深海.一类特殊结构对称矩阵三元组的逆二次特征问题[J].应用数学进展，2012,(1):18-27.

* 收稿日期：2016-02-01

DOI：10.13698/j.cnki.cn36-1037/c.2016.03.004

基金项目：中央财政支持地方高校发展专项基金项目；赣南师范大学研究生创新专项资金项目(YCX14B003)

作者简介：汪淑兰(1989-)，女，赣南师范学院数学与计算机科学学院硕士研究生，研究方向：代数理论及其应用；黄贤通，男，赣南师范学院与计算机科学学院教授，研究方向：矩阵理论及其特征反问题.

中图分类号：O302

文献标志码：A

文章编号：1004-8332(2016)03-0014-04

The Quadratic Inverse Eigen-Problem for Three Eigenpairs about a kind of Matrix

WANG Shulan, HUANG Xiantong

(SchoolofMathematics&ComputerScience,GannanNormalUniversity,Ganzhou341000,China)

Abstract:The paper studies the Quadratic Inverse Eigen-Problem basded on the three eigenpairs.The condition about existence of the solution was given and the expression under the condition of solution existence is obtained. The numerical experiment has been showed that the theoretical is correct.

Key words:eigenvalues; eigenvectors; eigenpairs; Quadratic Inverse Eigen-Problem

网络出版地址：http://www.cnki.net/kcms/detail/36.1037.C.20160510.1213.030.html