基于2个独立二项分布的风险比的信仰推断

汪永辉, 金　华, 吴　琴

(华南师范大学数学科学学院, 广州 510631)



基于2个独立二项分布的风险比的信仰推断

汪永辉, 金华*, 吴琴

(华南师范大学数学科学学院, 广州 510631)

摘要：2个独立二项分布参数之间的风险比的非劣效性检验在医学统计研究中是一个非常有意义的问题,常用的限制性极大估计方法在大多数情况下都不能控制第一类错误.文中提出用基于信仰推断法来解决基于2个独立二项分布参数之间的风险比的非劣效性检验问题.模拟结果显示:在小样本的研究情况下,这种基于信仰推断法的MF检验方法能很好地控制第一类错误,检验功效也不差.

关键词：二项分布; 非劣性检验; 信仰推断;p值; 功效

非劣效性检验在医学统计研究中主要关注新药疗效是否不比标准药差.假设用随机变量X0表示治疗某种疾病的标准药的疗效,用随机变量X1表示新药的疗效. 从研究病人中随机抽取n0和n1个病人分别用标准药和新药来治疗, 并假定标准药的治愈率是p0, 新药的治愈率是p1,则X0服从二项分布B(n0,p0),X1服从二项分布B(n1,p1).

上述问题可表示为2×2列联表(表1).表中,x0和x1分别为随机变量X0和X1的观测值. 医学研究中, 常常将p0和p1分别看成使用标准药和新药治疗某种疾病的风险, 这里讨论风险比:φ=p1/p0的单边非劣性假设检验问题:

H0:p1/p0≤φ0,H1:p1/p0≥φ1，

(1)

其中,0<φ0<φ1<1为事先指定的可接受边界值.式(1)表明当H0被拒绝时,新药的疗效并不比标准药差.

表1　治疗某种疾病的2种药物的治疗效果比较

MIETTINEN和NURMINEN[1]给出了假设检验问题(1)的基于讨厌参数p0的约束p1/p0=φ0极大似然估计的检验统计量(常称为MN检验)

zMN=

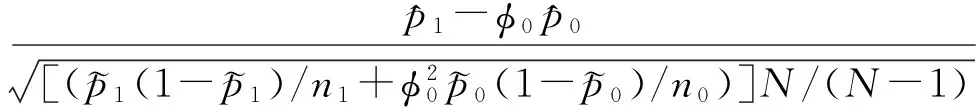
在原假设H0的条件下, 检验统计量zMN近似服从标准正态分布.因此当zMN≥z1-α(这里z1-α是标准正态分布的100×(1-α)分位点)时,在显著性水平1-α下,式(1)中原假设H0被拒绝,从而接受备择假设H1.文献[2-3]表明MIETTINEN和NURMINEN[1]的MN检验当样本量N较大时,表现良好. 但是这个检验统计量在样本量不太大的情况下不能很好地控制犯第一类错误的概率.

另一方面,有学者也利用贝叶斯方法来讨论假设检验问题(1).ZASLAVSKY[4]基于贝塔先验分布导出了2个独立二项分布的整数参数风险比精确后验分布,并给出了检验的p值:

PEB(φ=p1/p0≤φ0|x0,n0,x1,n1)=

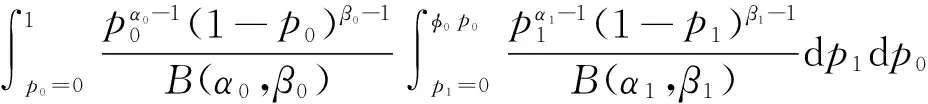
(3)

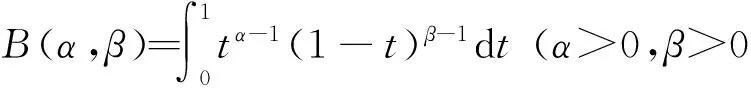
信仰推断法是FISHER[5]提出的一种统计方法.HANNIG等[6]发现信仰推断法可为小样本提供比较精确的推断结果.但是, 用信仰推断法研究关于2个独立二项分布风险比的假设检验问题, 目前国内外尚未见有相关报道.本文利用信仰推断法[6],在不涉及二项分布参数p先验分布的情况下,构造了2个独立二项分布的风险比的假设检验问题.模拟显示效果良好.

1基于信仰分布的检验方法

本节给出假设检验问题(1)的基于信仰分布的新检验方法.HANNIG[7]给出了二项分布参数p的信仰分布:

p=DU(x+1)+(1-D)U(x),

(4)

其中,D是服从均匀分布U[0,1]的随机变量,U1,…,Un是n个来自于U(0,1)的独立同分布的随机变量,U(x)是第x个次序统计量.U(x)的分布是贝塔分布Beta(x+1,n-x),U(x+1)的分布是Beta(x,n-x+1). HANNIG[7]通过模拟研究比较了几种不同D的选择,发现1个贝塔分布pSF=Beta(x+1/2,n-x+1/2)以及2个贝塔分布Beta(x+1,n-x)和Beta(x,n-x+1)的混合分布pMF=(Beta(x+1,n-x)+Beta(x,n-x+1))/2统计性质表现良好.下面基于上面2种不同的p的信仰分布,导出假设检验问题(1)的检验方法.

第1种情况, 如果二项分布参数p的信仰分布p～Beta(x+1/2,n-x+1/2),则有X0～Binomial(n0,p0),p0～Beta(x0+1/2,n0-x0+1/2);X1～Binomial(n1,p1),p1～Beta(x1+1/2,n1-x1+1/2).我们推导出的结果与贝叶斯学派使用Jeffreys先验分布Beta(1/2,1/2)得到的后验分布相同.于是,定义p值如下:

PSF(φ=p1/p0≤φ0|x0,n0,x1,n1)=

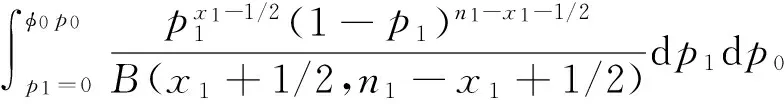
(5)

在给定检验水平α后, 当PSF(φ=p1/p0≤φ0|x0,n0,x1,n1)≤α时,我们拒绝H0,接受H1.

第2种情况,如果二项分布参数p是服从混合比为1/2的2个贝塔分布Beta(x+1,n-x)和Beta(x,n-x+1)的混合分布的随机变量,p～(Beta(x+1,n-x)+Beta(x,n-x+1))/2.这个信仰分布属于混合贝塔分布,其分布与贝叶斯学派使用任何先验分布求得的后验分布是不同的[8].此时,基于2个独立二项分布风险比φ=p1/p0的精确信仰分布是

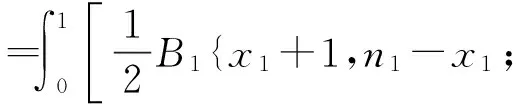
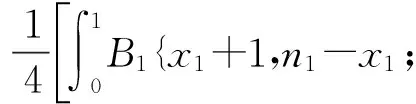
B1{x1+1,n1-x1;φp0}B0{x0,n0-x0+1;p0}dp0+

B1{x1,n1-x1+1;φp0}B0{x0+1,n0-x0;p0}dp0+

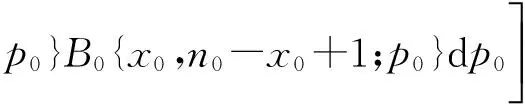
(6)

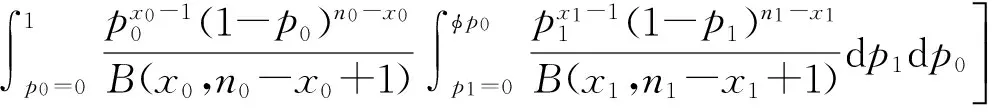
(7)

定义p值如下:

PMF(φ=p1/p0≤φ0|x0,n0,x1,n1)=

1.队伍问题。从成校方面看，目前成校教师大多由原小学、中学的专业教师转岗而来，专业性不强、年龄偏大，这些都影响整合的推进；从文化礼堂来看，管理人员往往兼任着社区里其他岗位的工作，工作繁杂，对和成校整合开展活动积极性不高。

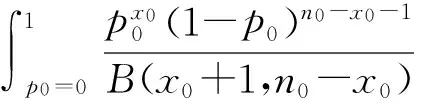
(8)

在给定检验水平α后,PMF(φ=p1/p0≤φ0|x0,n0,x1,n1)可以定出.当PrMF(φ=p1/p0≤φ0|x0,n0,x1,n1)≤α时,我们拒绝H0,接受H1.

2随机模拟

为了比较小样本情形下MIETTINEN和NURMINEN[1]的方法(简记为MN检验)、ZASLAVSKY[4]的方法(简记为EB)、基于信仰推断法的SF检验以及基于信仰推断法的MF检验的第一类错误和检验功效,本节利用统计软件R编程进行随机模拟，研究4种方法在样本量相等(n0=n1)情况下的第一类错误和检验功效. 有关参数p0,φ0以及φ1的取值参考了文献[9]. 随机模拟的结果见图1和图2.

为了考察4种方法的第一类错误,取n0=n1=20,25,30,50,φ0=0.8,0.9,和p0=0.3,0.3+0.01,0.3+0.02,0.3+0.03,…,0.8.取显著性水平α=0.05,在重复实验10 000次时,其置信水平为95%的置信区间(0.045 7,0.054 3).

图1表明,在样本量相等的小样本情形下：(i)MN检验的第一类错误率大部分都超过预先指定的显著性水平α=0.05的置信上限,不能很好地控制犯第一类错误; (ii)SF检验在参数p0的大多取值情况下,经常溢出预先指定的显著性水平α=0.05的置信上限；(iii)EB检验和MF检验的第一类错误率表现大部分是相同的,均能保证控制犯第一类错误.但是,EB检验在参数p0取一些比较小的值时,会溢出预先指定的显著性水平α=0.05.总的来说,就犯第一类错误而言,EB检验和MF检验要优于MN检验和SF检验.

比较4种检验的功效,在样本量相等的小样本情形下,取φ1=1.0和φ0=0.8,0.9,n0=n1=20,25,30,50.SF检验和EB检验的功效在大多数情况下相等,然而, EB检验在一些情况下功效高于SF检验;MN检验功效低于MF检验,尽管它们两者的功效有时会非常接近.MF检验的功效在n0=n1=20、p0的取值范围为0.40～0.65时会高于MN检验.因此,从功效来看,MF检验也并不比EB检验差多少.

下面给出一应用实例.考虑随机双盲抗血友病重组凝血因子VIIa的平行组研究[10]的数据.这项研究的主要目的是比较rVIIa 2种给药方案的治疗效果. 对于70 μg/kg组,x0=11,n0=31和对于35 μg/kg组,x1=4,n1=23. 设定非劣性检验的边界值φ0=0.91,我们来检验上面2组数据的非劣性假设检验问题：由式(2)可得频率方法中MN检验的p值为0.049 7;贝叶斯方法中EB检验的p值为0.050 2;信仰推断方法中的SF检验的p值为0.044 9;信仰推断方法中的MF检验的p值为0.048 8;比较了本文所得p值结果以及文献[4]159的例2的p值,发现这2个结果非常接近,可见本文方法的有效性.

3小结

针对传统的频率检验方法不能在小样本下控制第一类错误的问题以及贝叶斯方法中先验分布的主观性问题,本文将信仰推断法与2个独立二项分布参数风险比的单边非劣性假设检验相结合, 通过构建新的信仰单边非劣性假设检验,进而得到更加有效的检验方法.模拟结果显示:本文基于信仰推断法方法MF检验能很好地控制第一类错误,检验功效也不差;而目前常用的MN检验在大多数情况下都不能很好地控制第一类错误.

本文检验方法的样本量的计算公式,是一个值得进一步研究的问题.

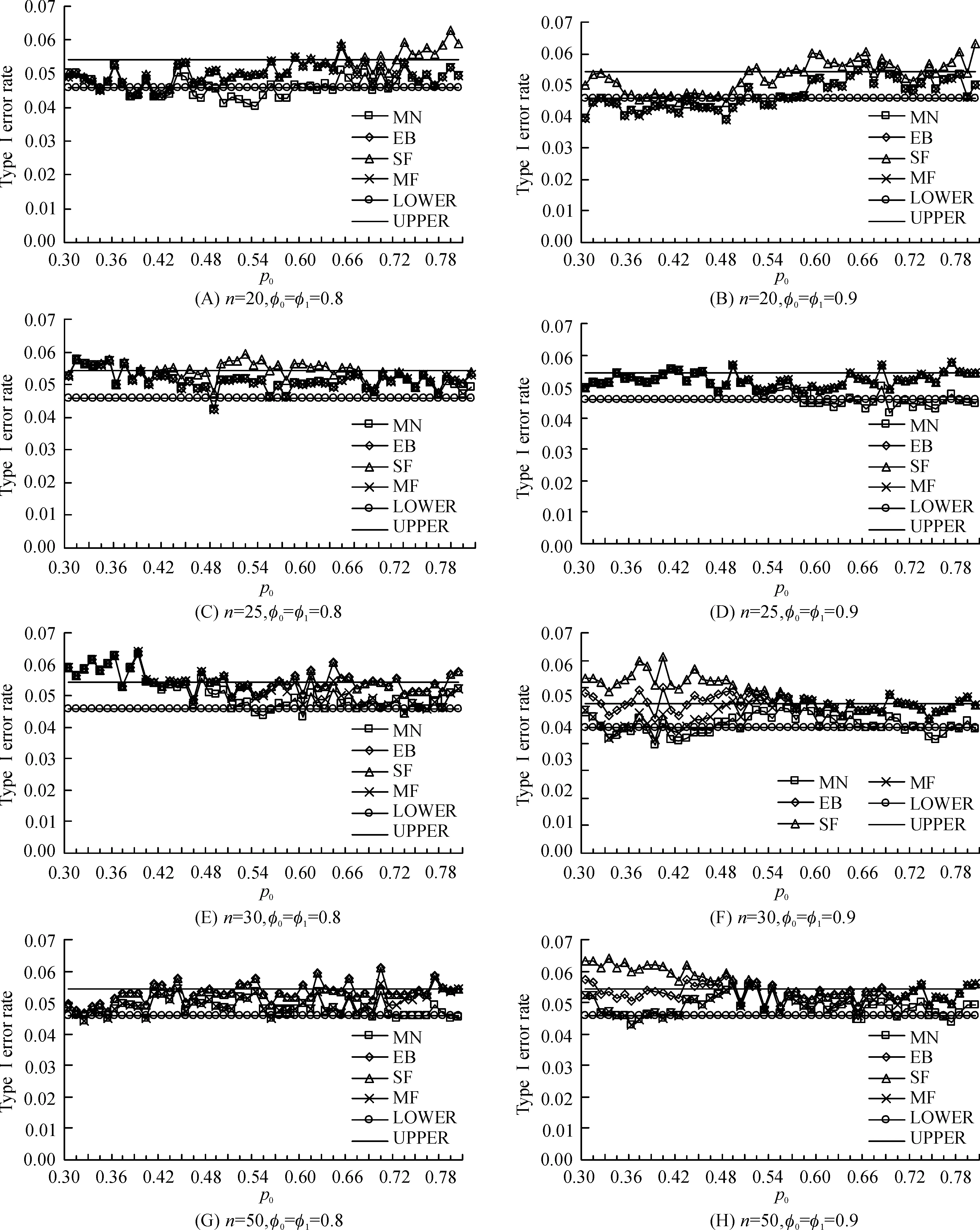
图14种检验方法在显著性水平0.05下的第一类错误率比较

Figure 1Comparison of Type I error rates of 4 test under significance level is 0.05

参考文献：

[1]MIETTINEN O, NURMINEN M. Comparative analysis of two rates[J]. Statistics in Medicine,1985，4(2):213-226.

[2]ALMENDRA-ARAO F, SOTRES-RAMOS D. Comparison of some non-inferiority asymptotic tests for two independent proportions[J]. Agrociencia, 2009,43(2):163-172.

[3]SOTRES-RAMOS D, ALMENDRA-ARAO F, RAMREZ-FIGUEROA C. Exact critical values for Farrington-Manning noninferiority exact test[J]. Drug Information Journal, 2010,44(2):159-164.

[4]ZASLAVSKY B G. Bayesian hypothesis testing in two-arm trials with dichotomous outcomes[J]. Biometrics, 2013,69(1):157-163.

[5]FISHER R A. Inverse probability[J]. Proceedings of the Cambridge Philosophical Society, 1930,26(4):528-535.

[6]HANNIG J, LAI R C S, LEE T C M. Computational is-

图24种检验方法在φ1=1.0下的检验功效比较

Figure 2Comparison of powers of 4 tests underφ1is 1.0

sues of generalized fiducial inference[J]. Computational Statistics & Data Analysis, 2014,71:849-858.

[7]HANNIG J. On generalized fiducial inference[J]. Statistica Sinica, 2009,19(2):491-544.

[8]GRUNDY P M. Fiducial distributions and prior distributions: an example in which the former cannot be associated with the latter[J]. Journal of the Royal Statistical Society: Series B, 1956,18(2):217-221.

[9]JIN H, FENG X B, CHEN M M, et al. Two new methods for non-inferiority testing of the ratio in matched-pair setting[J].TEST, 2014,23(4):691-707.

[10]LUSHER J M, ROBERTS H R, DAVIGNON G, et al. A randomized, double-blind comparison of two dosage levels of recombinant factor VIIa in the treatment of joint, muscle and mucocutaneous haemorrhages in persons with haemophilia A and B, with and without inhibitors[J].Haemophilia, 1998(4):790-798.

【中文责编：庄晓琼英文责编：肖菁】

Fiducial Hypothesis Testing for the Ratio of the Parameters of Two Independent Binomials

WANG Yonghui, JIN Hua*, WU Qin

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China)

Abstract：In medical statistics study, non-inferiority test for two independent binomial distribution parameters is a very important problem. The constrained maximum likelihood test statistic cannot control the type I error rates for some cases be investigated. In this article, the fiducial inference methodology is used in order to develop more powerful tests for non-inferiority based on the ratio between two independent binomial distributions. A broad Monte Carlo comparison between different tests for non-inferiority is presented, confirming the preference of the proposed method from a power perspective. Simulation studies suggest that the MF test can control the type I error rates and its empirical type I error rate are much closer to the prespecified nominal significance level than those of other tests well with competitive powers.

Key words：binomial proportions; non-inferiority test; fiducial inference;p-value; power study

收稿日期：2015-10-17《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

基金项目：国家自然科学基金青年项目(11401226)

*通讯作者:金华,教授, Email:jinh1@163.com.

中图分类号：O213.2;O213.8

文献标志码：A

文章编号:1000-5463(2016)01-0114-05