电润湿动力学描述及其非稳态研究进展

唐　彪， 赵　青， 周　敏， 李发宏, Robert A. HAYES, 周国富,2,3*

( 1.华南师范大学华南先进光电子研究院，彩色动态电子纸显示技术研究所，广州 510006;2.深圳市国华光电科技有限公司，深圳 518110；3. 深圳市国华光电研究院，深圳 518110)



电润湿动力学描述及其非稳态研究进展

唐彪1， 赵青1， 周敏1， 李发宏1, Robert A. HAYES1, 周国富1,2,3*

( 1.华南师范大学华南先进光电子研究院，彩色动态电子纸显示技术研究所，广州 510006;2.深圳市国华光电科技有限公司，深圳 518110；3. 深圳市国华光电研究院，深圳 518110)

摘要：电润湿作为极具前景的微流体操纵技术是近年持续的研究热点，其应用广布于光学滤光片、微变焦透镜、芯片实验室、印刷、光纤以及反射式显示器等重要光流器件领域．该文分析了主流能量最小化观点、热力学观点和电动力学观点对电润湿理论表达的区别和适用特点. 其中，电动力学观点对电润湿作用下三相接触线的移动行为赋予了明确的力学意义，适用于电润湿动态过程的描述. 文中重点对比了电润湿体系的动力学描述方法，整体能量平衡方法因其简单性和有效性可作为传统动力学理论建模手段的有力补充．电润湿动力学失稳现象主要由三相接触线附近电场分布畸变造成，同时介电层膜厚分布的不均性也会诱发电润湿动力学失稳. 在电润湿显示领域，动力学失稳引起的油墨破裂模式的差异已得到有效观测，其形成机理和控制技术研究具有重要应用意义. 最后，展望了电润湿基础理论及其动力学研究面临的挑战和研究方向.

关键词：电润湿； 动力学分析； 非稳态

早在1875年，LIPPMANN[1]根据在汞和电解液之间施加电压会出现电毛细管中汞液面下降的现象，提出了电毛细理论和著名的Young-Lippmann方程．但是由于该电毛细作用引起的接触角的变化范围很小以及当时无法克服的溶液电解问题，该理论并未得到广泛的重视．直到1993年，BERGE[2]在李普曼电润湿结构模型中引入了绝缘电介质层，有效消除了电解现象且大幅改善了液滴形状的操纵范围．这一被称为电介质上的电润湿(Electrowetting on Dielectric, EWOD)的技术突破了电极上电润湿的应用瓶颈，使电润湿理论和应用的研究进入了快速发展的新阶段．

随着对电润湿现象认识的逐步加深，围绕电润湿作用机理的研究逐渐形成了热力学观点、能量最小化观点和电动力学观点等主流学术观点．归结起来，前两者基于能量观点(即微液滴与介电层之间电荷积累产生的电容效应导致能量变化，引起微液滴表面张力改变从而使得接触角变化)[3]；而电动力学观点则认为微液滴在三相接触线上电荷累积产生的静电力导致微液滴毛细管线张力改变，从而引起接触角变化[4-5]．

随着理论的发展，各种电润湿应用技术应运而生．BERGE和PESEUX[6]发明了基于电润湿原理的微型液体透镜并已实现商业化应用； 2003年，HAYES等[7]报道了基于电润湿原理的彩色视频电子纸，引发了电润湿显示技术的研究热潮，而这仅仅是冰山一角．由于电润湿微流体器件具有调控范围宽、速度响应快、可靠性好和体积小等突出特点，其在光学、化学和电子学等诸多领域有着广泛的应用前景，如基于电润湿原理的光学滤光片、微变焦透镜、芯片实验室(Lab on Chip)、印刷、光纤以及反射式显示器等应用产品不断涌现．

目前，电润湿理论研究和应用已取得诸多进展，然而大部分的理论和实验研究集中在电润湿静态分析．而对于如电润湿显示、电润湿微透镜等大多数实际应用，电润湿系统中液体的动态响应对于器件性能的影响至关重要．如何有效描述电润湿动力学过程对于推进电润湿基础理论研究和提速电润湿应用技术开发具有重要意义．

1 电润湿理论基础

为描述润湿现象，YOUNG在1805年提出了Young方程：

γLVcosθ0=γSV-γSL,

(1)

其中，γLV、γSV和γSL分别是液-气、固-气和固-液界面的界面张力，θ0是固-液界面平衡接触角．

引入静电能的作用，可得Young-Lippmann方程(即电润湿控制方程)：

(2)

其中，θ是固-液界面接触角，θ0是固-液界面平衡接触角，ε0是真空介电常数，εr和d分别是疏水绝缘层的介电常数和厚度，V为施加的电压．热力学观点认为静电能是由液滴、疏水绝缘层和固体构成的电容被充电的结果[8]．

能量最小化观点认为，Bond常数B=ρgR2/γLV太小，重力对液滴自由能的影响可忽略不计．在没有电场力的情况下，液滴的运动过程主要由表面张力决定，其总自由能是液滴形状的函数[9].在电润湿体系中，液滴的自由能主要由电场能和界面能构成.

电动力学模型中静电场带来的电场力在液滴上的分布及其引起液滴接触角的变化具有明确的力学意义[9-13]．导电液滴在静电场中的受力分布情况可由Korteweg-Helmholtz方程[10]求得.

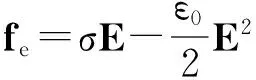
(3)

其中，σ为自由电荷体密度，E为电场强度，ε是液滴介电常数，ρ为液滴密度.式(3)右边第2项为有质动力；第3项为电致伸缩力．根据理论估算，固体表面三相接触线附近的电场力分布如图1所示，接触线附近电场力的水平分量将驱动液滴发生形变，直到与界面张力达到平衡．

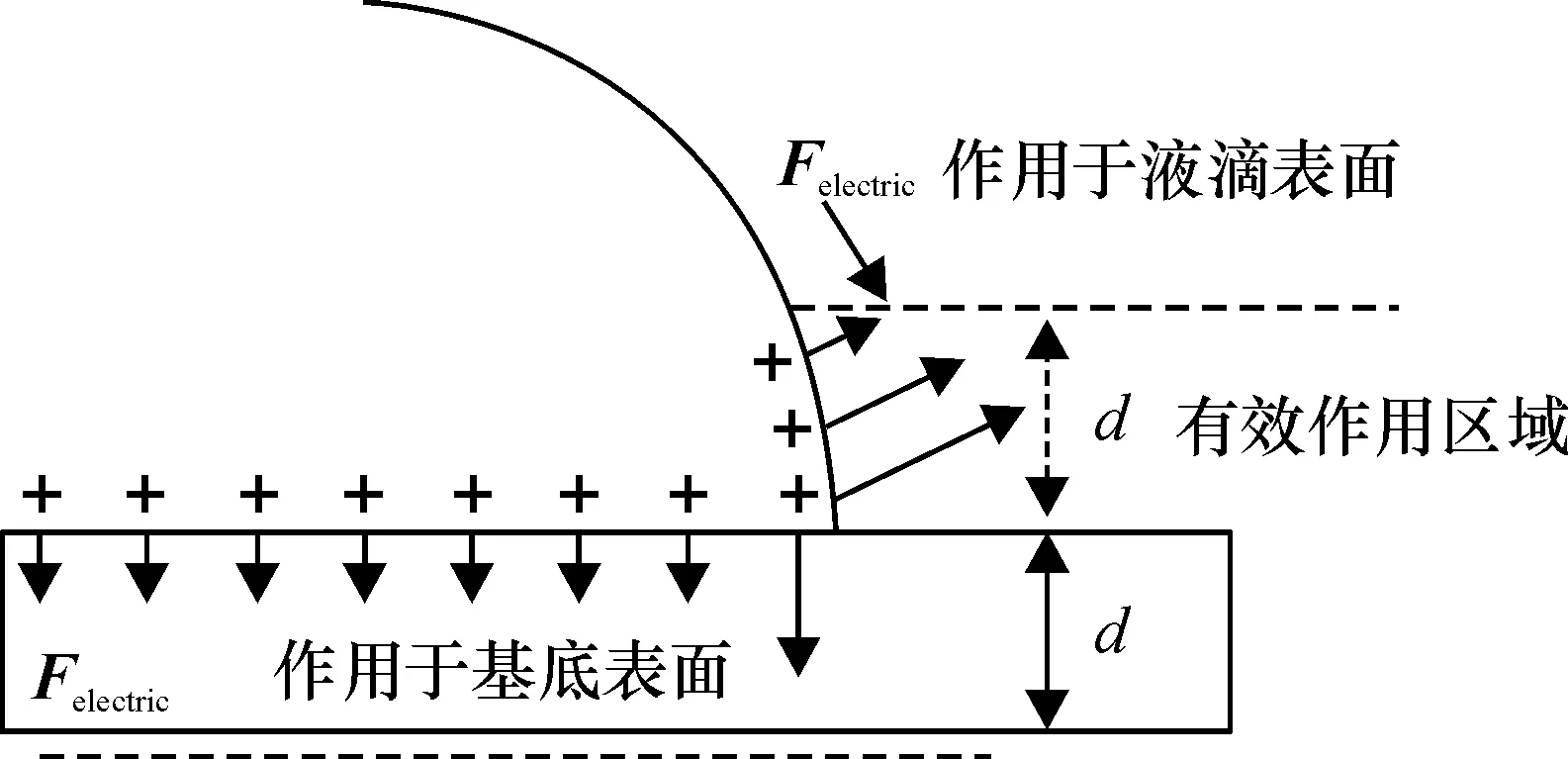
图1　固体表面三相接触线附近的电场力分布[9]714

Figure 1Electric field force distribution near the three-phase contact line of solid surface[9]714

能量最小化、热力学和电动力学的观点都可以推导电润湿的控制方程．其中能量最小化和热力学观点主要适合于对整个液滴的稳态过程进行分析，而不能像电动力学观点那样能够精确描述电场力对三相接触线的影响；电动力学的方法虽然能够预测液-气界面在距离三相接触线附近区域内会发生变形(KRUPENKIN[14]的研究结果表明弯曲确实存在)，但该方法忽略了实际情况中摩擦阻力对液滴的影响．

2电润湿体系的动力学描述

过去多数的理论和实验研究主要聚焦于电润湿体系的静态性能(或稳态性能)．然而，对于绝大多数以高响应、定量化微液滴操纵为目标的电润湿应用技术而言，体系的动力学响应同样至关重要．

2.1流体力学方法

流体力学理论是研究电润湿体系动力学响应过程的重要方法[15-19]. 例如，LOPEZ-HERRERA等[17]提出了一种使用流体体积法(VOF)来解决两相之间电流体动力学(EHD)问题的模型．通过假设所涉及的流体是纯粹的电介质(绝缘体)或完美的导体，使用“Taylor-Melcher漏电介质模式”这一惯常假设忽略电荷对流对欧姆传导的影响，提供了一种准确的电流体动力学计算方法．该电流体动力学方法采用流体体积法来解决不可压缩流体的运动，结合了Navier-Stokes方程中的电场力，而且通过传导和对流的电荷守恒方程来考虑电荷迁移．然而，对于该方法涉及的接触角在三维空间的明确定义存在难度，对三相接触线的运动难以有效模拟和预测(图2)．当前，大部分流体力学方法通常对液滴收缩和惯性作用占主导的液滴铺展的初始阶段的动力学特点可以有效描述.然而，传统流体力学模型未考虑三相接触线的作用，且未充分考虑电毛细效应或者没有提供合适的模型来计算固液界面的粘性阻力[18]．

图2计算机模拟图片与2 mm直径的水滴撞击固体表面的照片对比[18]653

Figure 2Computer generated images compared with photographs of a 2mm diameter water droplet impacting a solid surface[18]653

近年来，一些基于流体动力学的数字模拟方法在电润湿体系动力学建模领域得到了成功应用[20-21]. 利用各种数字模拟方法求解纳维-斯托克斯方程可以较好地预测整个电润湿过程．例如ROGHAIR[20]使用流体体积法处理不同的流体相，在OpenFOAM框架成功模拟了电润湿动态响应过程. 通过电荷传输方程和高斯定律,流体界面的电场力基于流体动力学求解得到有效考量和计算.模拟与实验结果表明，该模型在15、20、25 V外加电压下可以较好地描述像素开启(图3)和关闭(图4)的动力学过程. 然而，由于涉及的数值求解过程相当复杂，该方法的应用受到较大限制.

图3　液滴在25 V时的开启过程[20]480

图 4　液滴的铺展过程[20]476

2.2总体能量平衡方法

较为简单的总体能量平衡方法(OBE)可以很好地模拟液滴在固体基板上的铺展过程[21-22]，已成功用于电润湿过程[23-24]的动力学描述.通常电润湿系统的OEB方程表达为：

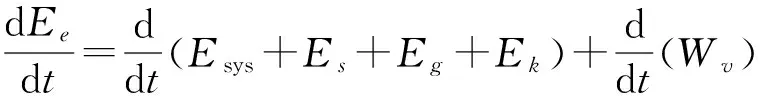
(4)

其中，Ee,Esys,Es,Eg,Ek和Wv分别表示电场能、内能、界面能、重力势能、动能和粘性耗散作用．由于电润湿系统中油滴质量和温度保持不变，因此ΔEs=0．由文献[8]4393的分析：C(V)≈CAF/water(V)，则电场能随时间的变化为：

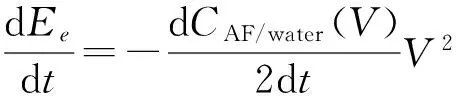
(5)

其中，C表示电容．假设液滴保持球冠形则液滴的重力势能随时间变化可以表示为[22]113

(6)

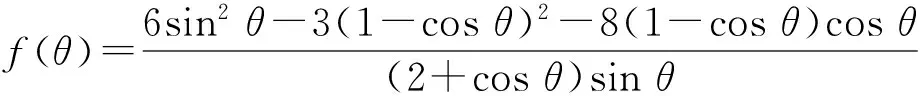
(7)

其中，m为液滴的质量．根据文献[25]的分析得到接触线摩擦力，则单位时间粘性耗散功可表示如下：

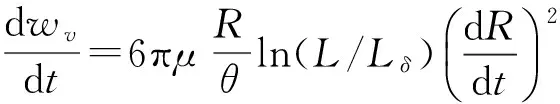
(8)

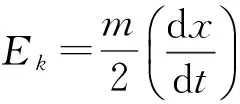
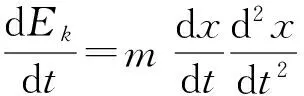
(9)

系统的总表面能相当于3个相界面(流体-固体，流体-气体和气体-固体)的自由能之和[21]，然后对表面能进行积分得

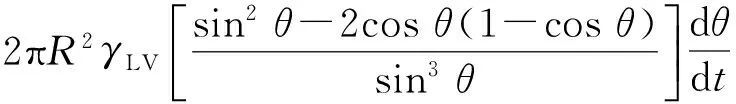
(10)

将式(6)～(9)代入方程(10)得到OBE方程：

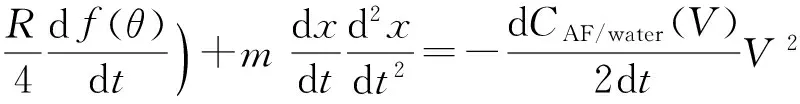
(11)

总体能量平衡(OBE)方法可以很好地分析各种能量对电润湿系统的贡献，且可以在能量平衡方法的基础上建立预测电润湿动力学响应过程的几何模型．GU和LI[21]利用简单的能量平衡方法很好地模拟了油墨铺展过程中接触角(θ)、半径(R)、高度(H)随时间的变化过程(图5)．

较简单的总体能量平衡方法克服了流体力学模型没有考虑三相接触线影响的不足，并有效地避免了复杂的数字模拟过程．但对于这些简单的模型，三相接触线的运动太过复杂，因此在这些模型中不可避免地采取依赖一定经验参数的近似．

图5　液滴在基板界面铺展的动力学过程[21]252

3动力学非稳态研究

电润湿过程中液滴与基板之间的接触线附近可在一定大小的范围内失去稳定性，导致小液滴从大液滴的边缘分离[26-27]．在一般情况下，由于拉普拉斯压力梯度的影响，任意形状的液体表面都会出现动力学非稳现象，在母体液滴周围产生固着在母体的活力较强的小液滴(图6)．

图6　从母体产生的卫星滴[27]2304

文献[28-29]认为三相交界处电荷密度的不均性导致了附近横向电场的变化.在达到某个电压阙值后接触线变得不稳定，该效应使得固着在母体上活力较强的小液滴出现震颤现象，并最终逃逸出母体形成卫星滴．

3.1电场不均引起的动力学失稳

根据电润湿的物理力学机制，电场力是液滴在电介质上发生电润湿现象的主要驱动力，因此电场不均是引起液滴在电润湿过程中出现不稳定性的重要原因. STAICU和MUGELE[30]研究了油相环境中水滴在平滑疏水表面的铺展过程，发现在水滴下方有一层非常薄的油墨滞留现象.为了描述该层油膜的陷入和滞留过程，引入附加电场力作用扩展了Landau-Levich定理来处理动态润湿过程[31]. 随着滞留的发生，油膜变得不稳定并破裂成许多更小的液滴(图7).这些液滴的尺寸分布可以通过基于润滑近似的薄膜线性稳定性分析表述.该问题可以用2个阶段来描述：油膜的流体动力学捕获过程和随后油膜的非稳态演变过程．

图7施加电压过程中选取不同时刻液滴在基板界面上的显微镜图像[30]168

Figure 7The optical microscope images of the position change of droplets at different time in the process of applying voltage[30]168

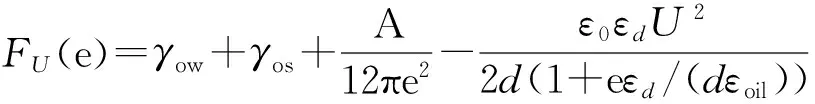
(12)

其中，e是油膜厚度，ε0是真空介电常数，εoil是油膜介电常数，εd和d分别是疏水绝缘层的介电常数和厚度，U为施加的电压．式(12)的第4项是有油膜层和电介质层为介质的平行于基板的电容器充电后的静电能量；第3项为范德瓦尔斯作用，其对油膜稳定性的影响取决于常数A[32]．可见，静电能分布不均将导致系统的自由能非稳态是电润湿过程中出现动力学非稳的重要原因．

3.2介电层厚度不均引起的动力学失稳

电润湿结构中的疏水绝缘介质层通常由高分子聚合物薄膜构成[34]. 该层薄膜的稳定性是由其表面起伏的瞬态行为决定的.通常液体的表面形貌不是理想的平面状态，分子布朗运动导致的毛细波频谱一直存在(图8). 如果施加一个外力耦合到初始毛细波频谱，该波动则可能放大或衰减. 重力、表面张力、范德华力、电场/磁场等外力以及作用在界面温度梯度等因素的相互作用在界面上形成应力并导致薄膜的失稳.

通常，高分子聚合物薄膜的不稳定性对其应用是不利的，并被试图通过各种方案加以抑制[35].然而，如果薄膜的非稳定性可以得到精确的控制，则可利用薄膜结构自发形成过程中出现的不稳定性来产生技术上需要的新型特定结构[36-38]，这在科研和工业应用中都有重要的价值.

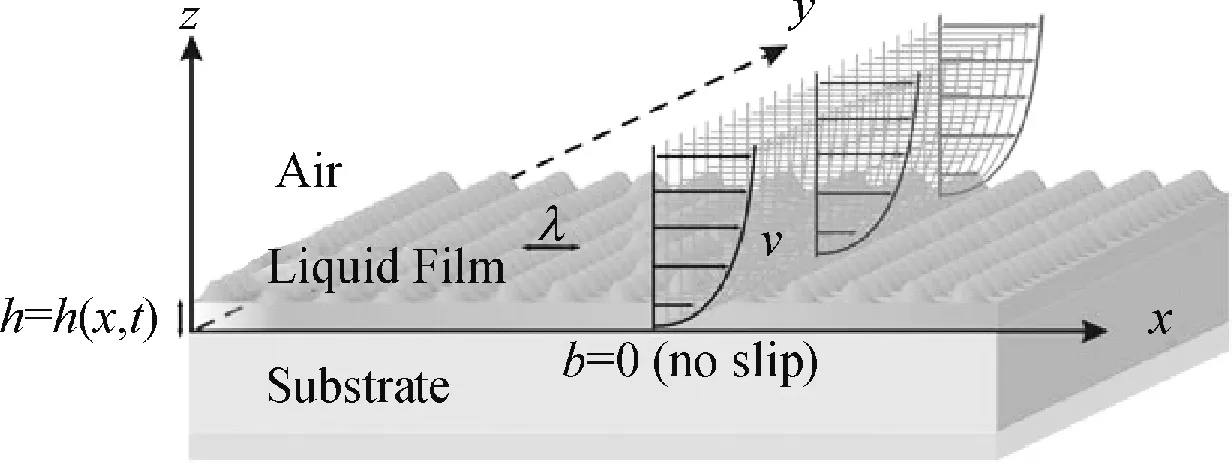
图8　厚度h的聚合物薄膜的示意图[34]15Figure 8　A schematic view of a polymer film of thicknessh[34]15注:为温度波动诱导薄膜表面毛细波动波长.

3.3液滴粘度与动力学失稳

电润湿过程中的不稳定性因素除了电场不均和聚合物薄膜缺陷外，还有着其他因素的影响．最具代表性的有：降低液滴粘度对交流电润湿动态振荡过程的影响[39]．降低液滴粘度对振荡动力学的影响主要在共振频率和振荡幅度，基于实验和理论模型对不同的交流电压和频率对液滴振荡动态进行了对照研究．实验结果表明，粘度下降很少影响共振频率，但强烈影响共振频率的振幅和峰的宽度．此外，当液滴粘度降低超过临界值时，增大施加的交流电压，液滴振荡的谐振模式不再观察到．最后，经实验观察和经验得出，其中最大振幅与液滴粘度成反比关系．

在这项研究中，用电润湿数η=εε0V2/(2dγ)(ε为绝缘层介电常数，ε0为真空介电常数，V为施加电压，d为绝缘层厚度，γ为液滴表面张力)代替施加电压．图9显示了在η=0.25时，5 μL不同粘度的液滴分别在32 Hz和98 Hz的交流电作用下的振荡行为．液滴粘度为1 mPa·s的5 μL液滴在2种不同频率下的振荡行为分别对应于图9A的P2模式和图9B的P4模式的谐振频率．可见，液滴振荡幅度随粘度增加而显著下降，且频率较低模式下的振荡幅度明显大于高频率模式[39-40]．

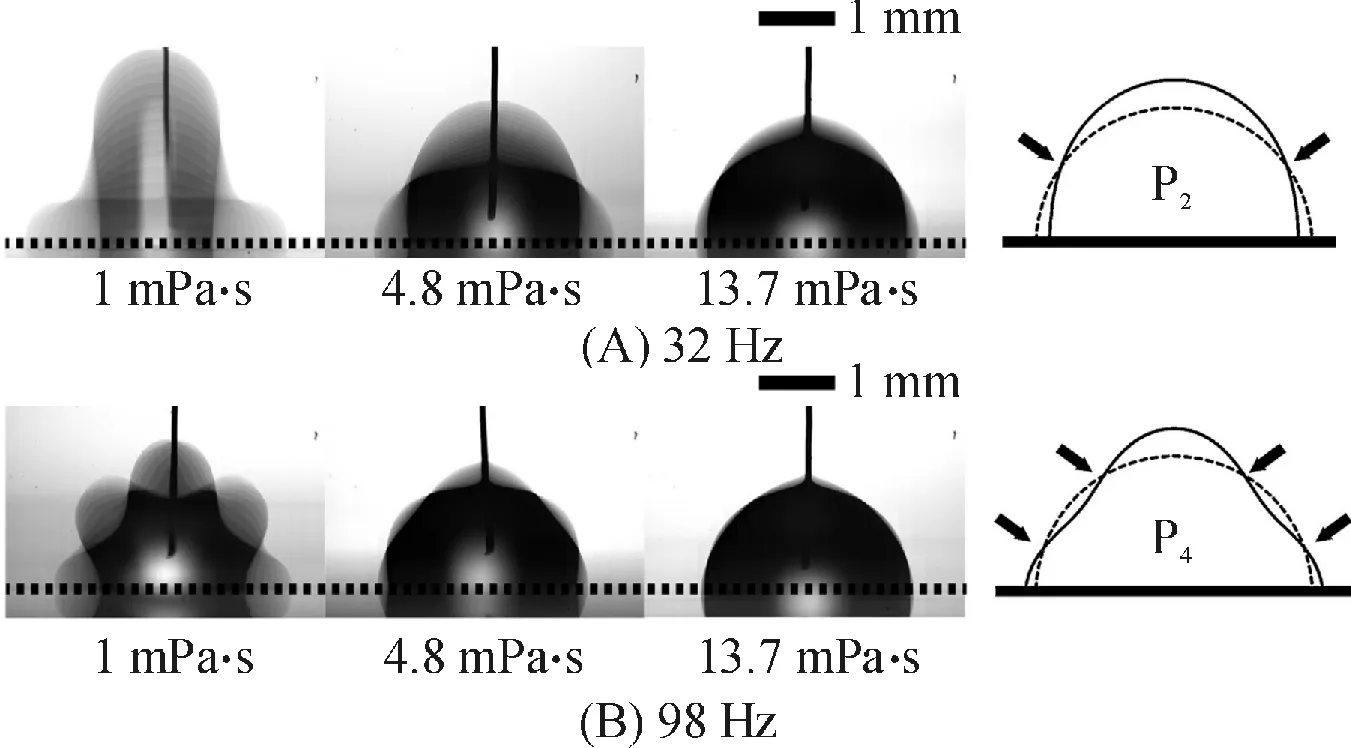
图9　5 μL不同粘度的液滴在不同频率的振荡模式[39]50

Figure 9Oscillation patterns of 5 μL drops with different viscosities frequencies[39]50

3.4电润湿显示技术中的动力学非稳现象

电润湿显示是通过外加电场控制油墨在像素单元内有效覆盖的比例来实现光学开关和灰度控制的效果．通常，对于电润湿显示器件的开口率等理论计算模型大多基于像素内油墨保持球冠形状的假设来进行．然而，在实际观察中可以发现，电润湿显示像素的光学开启过程是从油膜的破裂开始的．而且，不同像素尺寸的电润湿显示屏样品在特定电压下会产生不同的开启模式，这已在ROGHAIR等[20]的实验结果中得到证实．与我们传统的油墨几何模型的假设大相径庭，也为重新认识和优化电润湿显示器件的动力学表现提供了机遇.

笔者所在课题组在研究中也证实电润湿显示中油水界面的动力学非稳现象(表现为特定电压下像素油膜破裂的位置和形状不同)，并正在探索相关理论机理.图10为像素长宽比为1∶1、2.1∶1、4.7∶1的显示屏样品在特定电压下产生的不同开启模式.通过理论与实验数据比较，发现了一些以前未被报道的现象. 例如，从施加电压至像素光学响应之间存在一个显著的诱导时间(大约为5 ms)(图11).以上发现以及后续的理论探索，将为非开放式电润湿体系的应用开发提供广泛的指导意义.

图10　电压相关的电润湿显示像素开启模式

Figure 10Applied-voltage dependent switch-on modes of EFDs

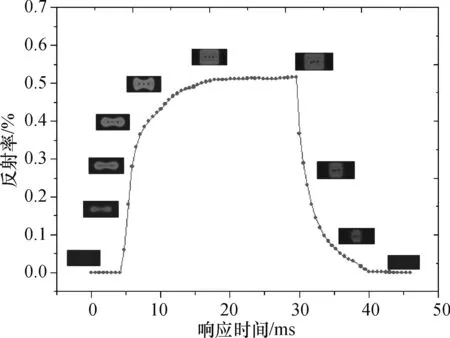
图11　电润湿显示器件光电响应测试曲线

注：施加电压为25 V, 像素尺寸315 μm×150 μm.

4总结与展望

电润湿是非常高效且易操控的微流体工具，是近年的研究热点．能量最小化和热力学观点适用于电润湿行为的稳态分析.电动力学观点对电润湿作用下三相接触线的移动行为赋予了明确的力学意义，成为描述液滴的电润湿动态过程有力工具．然而，如何在电润湿过程中引入粘性耗散等阻力的影响依然未能形成统一的理论支撑，有待进一步研究.依赖一定经验参数的整体能量平衡方法克服了流体力学模型对三相接触线影响忽略考量的不足，有效避免了复杂的数字模拟过程，是传统电润湿体系动力学描述方法的有力补充．但如何对电润湿体系动力学进行精确物理描述仍然是一个挑战．电润湿过程中出现的动力学失稳现象主要由三相接触线附近电场分布畸变造成，同时介电层膜厚分布的不均性也会诱发电润湿动力学失稳．电润湿动力学失稳引起的油墨破裂模式的差异被实验验证，相关特定模式形成机理与控制技术的成熟将为电润湿显示驱动技术的优化提供重要指导意义.

参考文献：

[1]LIPPMANN G.Relation entre les phénomènes électriques et capillaries[J]. Annales de Chimie et de Physique, 1875, 5(11):494-549.

[2]BERGE B．Electrocapillarity and wetting of insulator films by water[J]． Comptes Rendus De L′académie Des Sciences: Serie II, 1993, 317 (2): 157-163.

[3]WALKER S W, SHAPIRO B.Modeling the fluid dynamics of electrowetting on dielectric (EWOD)[J]. Journal of Microelectromechanical Systems, 2006, 15: 986-1000.[4]DIGILOV R. Charge-induced modification of contact angle: the secondary electrocapillary effect[J]. Langmuir, 2000, 16:6719-6723.

[5]JONES T B. An electromechanical interpretation of electrowetting[J]. Journal of Micromechanics and Micro-engineering, 2005, 15:l184-l187.[6]BERGE B, PESEUX J．Variable focal lens controlled by an extemal voltage：an application of electrowetting[J]. The European Physical Journal E，2000, 3(2):159-163.[7]HAYES R A, FEENSTRA B J. Video-speed electronic paper based on eleetrowetting[J]. Nature, 2003, 425: 383-385.

[8]CARMES T R, HAYES R A, FEENSTRA B J, et al. Liquid behavior inside a reflective display pixel based on electrowetting[J]. Journal of Applied Physics, 2004, 95(8):4389-4396.

[9]MUGELE F, BARET J C. Electrowetting: from basics to applications[J]. Journal of Physics: Condensed Matter, 2005, 17:705-774.

[10]JONES T. On the relationship of dielectrophoresis and electrowetting[J]. Langmuir, 2002, 18:4437-4443.[11]KANG K H. How electrostatic fields change contact angle in electrowetting[J]. Langmuir, 2002, 18:10318-10322.[12]ZENG J, KORSMEYER T. Principles of droplet electrohydrodynamics for lab-on-chip[J]. Lab on A Chip, 2004, 4(4):265-277.

[13]OH J M, KO S H, KANG K H. Analysis of electrowetting-driven spreading of a drop in air[J]. Physics of Fluids, 2010, 22(03):Art 032002,10pp.

[14]KRUPENKIN T N. From rolling ball to complete wetting: the dynamic tuning of liquids on nanostructured surfaced[J]. Langmuir, 2004, 20:3824-3827.

[15]TOMAR G, GERLACH D, BISWAS G, et al. Two-phase electrohydrodynamic simulations using a volume-of-fluid approach[J]. Journal of Computational Physics, 2007, 227:1267-1285.

[16]LIMA N C, D’AVILA M A. Electric effects on conducting newtonian and viscoelastic droplets[C]∥22nd International Congress of Mechanical Engineering. Ribeirao Preto, Brazil, 2013.

[17]LOPEZ-HERRERA J M, POPINET S, HERRADA M A. A charge-conservative approach for simulating electrohydrodynamic two-phase flows using volume-of-fluid[J].Journal of Computational Physics,2011,230:1939-1955.[18]PASANDIDEH-FARD M, QIAO Y M, CHANDRA S,et al. Capillary effects during droplet impact on a solid surface[J]. Physics of Fluids, 1996, 8:650-659.

[19]KESHAVARZ-MOTAMED Z, KADEM L. A effects of dynamic contact angle on numerical modeling of electrowetting in parallel plate microchannels[J]. Microfluidics Nanofluidics, 2010, 8(1):47-56.

[20]ROGHAIR I, MUSTERD M, ENDE M D, et al. A numerical technique to simulate display pixels based on electrowetting[J]. Microfluidics Nanofluidics, 2015, 19:465-482.

[21]GU Y, LI D. A model for a liquid drop spreading on a solid surface[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1998, 142:243-256.[22]ERICKSON D, BLACKMORE B, LI D. An energy balance approach to modeling the hydrodynamicall y driven spreading of a liquid drop[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2001, 182:109-122.

[23] LEE L, MOON H, FOWLER B,et al. Electrowetting and electrowetting-on-dielectric for microscale liquid handling[J]. Sensors and Actuators A:Physical, 2002, 95(2/3):259-268.[24]BAHADUR V, GARIMELLA S V. An energy-based model for electrowetting-induced droplet actuation[J]. Micromech Microeng, 2006, 16:1494-1503.

[25]BROCHARD-WYART F, GENNES P G. Dynamics of partial wetting[J]. Advances in Colloid and Interface Science, 1992, 39:1-11.

[26]PARK J, FENG X Q, LU W. Instability of electrowetting on a dielectric substrate[J]. Journal of Applied Physics, 2011, 109:034-309.

[27]MUGELE F, HERMINGHAUS S. Electrostatic stabilization of fluid microstructures[J]. Applied Physics Letters, 2002, 81:2303-2305.

[28]VALLET M, VALLADE M, BERGE B. Limiting phenomena for the spreading of water on polymer films by electrowetting[J]. European Physical Journal B, 1999, 11:583-591.

[29]JAMES A J, VUKASINOVIC B, SMITH M K, et al. Vibration-induced drop atomization and bursting[J]. Journal of Fluid Mechanics, 2003, 476:1-28.

[30]STAICU A, MUGELE F. Electrowetting-induced oil film entrapment and instability[J]. Applied Physics Letters, 2006, 97(16):167-801.

[31]MALEKI M, REYSSAT M, RESTAGNO F, et al. Landau-Levich menisci[J]. Journal of Colloid and Interface Science, 2011, 354:359-363.

[32]QUILLIET C, BERGE B. Investigation of effective interface potentials by electrowetting[J]. Europhysics Letters, 2002, 60:99-105.

[33]HERMINGHAUS S. Dynamical instability of thin liquid films between conducting media[J]. Applied Physics Letters, 1999, 83:2359.

[34]OPPENHEIMER P G. Electrohydrodynamic patterning of functional materials[D]. Cambridge: University of Cambridge,2013.

[35]YERUSHALMI-ROSEN R, KLEIN J, FETTERS L. Suppression of rupture in thin, nonwetting liquid films[J]. Science, 1994, 263:793-795.

[36]BOLTAU M, WALHEIM S, MLYNEK J, et al. Surface-induced structure formation of polymer blends on patterned substrates[J]. Nature, 1998, 391:877-879.

[37]CHOU S, ZHUANG L, GUO L.Lithographically induced self-construction of polymer microstructures for resistless patterning[J].Applied Physics Letters,1999, 75(7)：1004-1006.[38]CHOU S, ZHUANG L. Lithographically-induced self-assembly of periodic polymer micropillar arrays[J]. Journal of Vacuum Science & Technology B, 1999, 17:3197- 3202.[39]HONG J,KIM Y K,KANG K H,et al.Effects of drop viscosity on oscillation dynamics induced by AC electrowetting[J].Sensors and Actuators B:Chemical,2014,190:48-54.

[40]OH J M, KO S H,KANG K H. Shape oscillation of a drop in ac electrowetting[J]. Langmuir, 2008, 24:8379-8386.

【中文责编：庄晓琼英文责编：肖菁】

Research Progress in Electrowetting Dynamics and Its Instability

TANG Biao1，ZHAO Qing1, ZHOU Min1, LI Fahong1, Robert A. HAYES1, ZHOU Guofu1,2,3*

(1. Institute of Electronic Paper Displays, South China Academy of Advanced Optoelectronics, South China Normal University, Guangzhou 510006, China;2.Shenzhen Guohua Optoelectronics Tech.Co.Ltd.，Shenzhen 518110，China ；3.Academy of Shenzhen Guohua Optoelectronics，Shenzhen 518110，China)

Abstract：Electrowetting as the most promising microfluidic manipulation technique, has been a hot research topic and shows attractive potential in various optofluidic applications, such as optical filters, micro lens, lab on a chip, printing, optical fiber, and reflective displays, etc. In the present review, the differences and applicable features of the mainstream academic point of views in electrowetting theory, including energy minimization, thermodynamic approach and electromechanical method are addressed. Electromechanical method gives a clear sense of mechanics to the evolution behavior of three-phase contact line, which enables the dynamic description of electrowetting process. The dynamic descriptions of electrowetting system are discussed and compared. Since its simplicity and effectiveness, the overall energy balance approach could be a powerful option for dynamics modeling of electrowetting system. The mechanism of dynamics instability in electrowetting is fully discussed. The electric field distortion near the three-phase contact line and the unevenness in dielectric layer thickness mainly contribute to the dynamics instability phenomenon. Different modes of oil break have been observed and shown potential controllability, which may help the development of electrowetting displays. The challenges and potential research directions in the field of electrowetting fundamental theory and its dynamics have been highlighted.

Key words：electrowetting; dynamic analysis; instability

收稿日期：2015-12-31 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

基金项目：国家自然科学基金项目(51405165)；教育部“长江学者和创新团队发展计划”项目(IRT13064)；广东省引进创新科研团队计划项目(2011D039)

*通讯作者:周国富，教授，国家“千人计划”入选者、广东省领军人才，Email：zhougf@scnu.edu.cn.

中图分类号：TN27

文献标志码：A

文章编号:1000-5463(2016)01-0035-07