具有极大P-集的实对称阵及其伴随图

杜志斌

(肇庆学院数学与统计学院，肇庆 526061)



具有极大P-集的实对称阵及其伴随图

杜志斌*

(肇庆学院数学与统计学院，肇庆 526061)

摘要：实对称阵的P-集是一个基于矩阵的特征值重数以及Cauchy插值定理所提出的定义．设A为一个n阶实对称阵，记mA(0)为A的特征值为0的(代数)重数，并记A(S)为将A的第i1,i2,…,ik行与第i1,i2,…,ik列去掉后所得的主子阵，其中S={i1,i2,…,ik}为{1,2,…,n}的一个非空子集．特别地，当mA(S)(0)=mA(0)+|S|时，称S为A的一个P-集．记PS(A)为实对称阵A的P-集所含元素个数的最大值．基于每个n阶实对称阵至多包含⎣n/2」个元素，文中研究了满足PS(A)=⎣n/2」的n阶实对称阵A的结构特点，进而给出此类矩阵的若干性质，并对n为偶数时A的伴随图进行特征刻画，而对n为奇数时A的伴随图给出了猜想，推广了具有极大P-集的树矩阵的相关结果．

关键词：实对称阵； 伴随图； 特征值重数； P-集

给定一个n阶实对称阵A，根据A的主对角线以外的元素的零位模式，可定义A的伴随图，具体来说，n阶实对称阵A=(aij)的伴随图是以V={1,2,…,n}为点集，以E={ij|i≠j,aij≠0}为边集的无向简单图．特别地，若实对称阵A的伴随图为树，则称A为树矩阵．

反过来，给定一个具有n个点的无向简单图G，可定义出一个相应的实对称矩阵类：

S(G)={A|A是一个n阶实对称阵,且A的伴随图为G}．

显然，S(G)中矩阵的主对角线元素可任意选取,各个矩阵的主对角线以外的元素的零位模式是一致的，并由图G唯一决定．

对于任意实对称阵A，若0是A的一个特征值，则记mA(0)为特征值为0的(代数)重数．此外，若0不是A的特征值，则习惯上记作mA(0)=0．

设S={i1,i2,…,ik}为{1,2,…,n}的一个非空子集，现将n阶实对称阵A的第i1,i2,…,ik行与第i1,i2,…,ik列去掉，所得的主子阵记为A(S)．根据Cauchy插值定理[1] 242-243，可得

其中S为{1,2,…,n}的一个非空子集．JOHNSON等[2]353将满足

mA(S)(0)=mA(0)+|S|

的集合S称为实对称阵A的一个P-集．特别地，若S是实对称阵A的P-集，且S只含一个元素，比如S={i}，则称i为A的一个P-点．

根据Cauchy插值定理，显然P-集的每个元素都是P-点，但在一般情况下，若干个P-点所组成的集合并不是P-集．FERNANDES与DA CRUZ[3]、NELSON与SHADER[4]分别给出了若干类矩阵，使其任意多个P-点所组成的集合是P-集．

此外，P-集所含元素个数也是一个研究热点．JOHNSON等[2]给出了树矩阵的P-集所含元素个数的下界．而在研究实对称阵的P-集所含元素个数的上界时，KIM与SHADER定义了PS(A)，表示实对称阵A的P-集所含元素个数的最大值[5]400；证明了PS(A)≤⎣n/2」，其中A为任意n阶实对称阵，而且上界⎣n/2」可达[5]402-403．

文献[6]研究了满足PS(A)≤⎣n/2」的n阶树矩阵A，完全刻画出A的伴随图(树)．有趣的是，这些树恰恰是匹配数为⎣n/2」的树．本文将研究范围从树矩阵延伸到所有实对称阵，研究了满足PS(A)≤⎣n/2」的n阶实对称阵A，给出其相关性质，并对n为偶数时A的伴随图进行特征刻画，而对n为奇数时A的伴随图给出了猜想，推广了树矩阵的相关结果[6]．

1预备知识与引理

首先介绍2个重要引理．

引理1[6]29-30设A为n阶实对称阵，则PS(A)≤⎣n/2」．特别地，若PS(A)≤⎣n/2」，且α是A的一个P-集，|α|=⎣n/2」，则有下述情形之一：

(i)n为偶数，且mA(0)=0，从而mA(α)(0)=n/2，这表明A(α)的秩为0，即A(α)=0；

(ii)n为奇数，且mA(0)=1，从而mA(α)(0)=(n+1)/2，这表明A(α)的秩为0，即A(α)=0；

(iii)n为奇数，且mA(0)=0，从而mA(α)(0)=(n-1)/2，这表明A(α)的秩为1．

给定一个m×n矩阵A，记ρA为A的项秩，即矩阵A中两两不在同一行或者同一列的非零元素的最大个数．特别地，若rank A=m，则ρA=m．

设A、B皆为m×n矩阵，则由文献[1]13知:

rank(A+B)≤rankA+rankB．

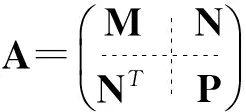
证明首先有

等价地，

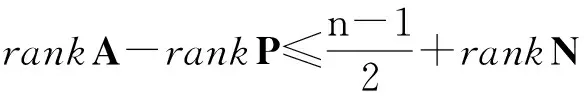
即

□

2主要结果

首先考虑矩阵阶数为偶数时的情形．

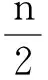
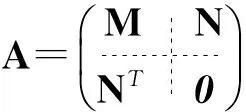
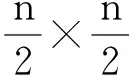
注意到，

|A|=(-1)n2/4|N|·|NT|=(-1)n2/4|N|2.

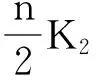
现取V=α，结果可证．

□

下面考虑矩阵阶数为奇数时的情形．

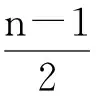
由引理1(ii)、(iii)，可得A(α)的秩为0(即A(α)=0)或为1．

情形1：A(α)的秩为0，即A(α)=0．

首先，由A(α)=0可知G(α)为空图，且A的结构如下：

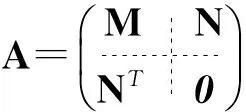
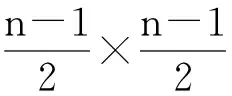
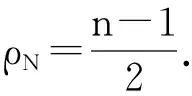
现取V=α，结果可证．

情形2：A(α)的秩为1．

首先，由A(α)的秩为1，以及A为实对称阵，可知G(α)包含一个完全图(可能只含一个点)以及若干个孤立点．

此外，A的结构如下：

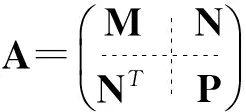
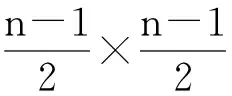
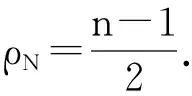
现取V=α，结果可证．

□

设G为具有n个点的图，当n为偶数时，定理1给出了S(G)中存在实对称阵A且PS(A)=n/2的一个必要条件．事实上，这也是S(G)中存在实对称阵A使得PS(A)=n/2的一个充分条件．于是有下述定理．

定理3设G为具有n个点的图，其中n为偶数．下述2个条件是等价的：

(a)S(G)中存在实对称阵A使得PS(A)=n/2；

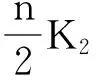
证明由定理1可得(a)⟹(b)．下面证明(b)⟹(a)．设G满足条件(b)，且不妨设V={1,2,…,n/2}．

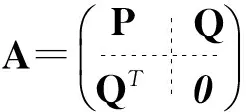
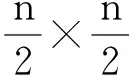
此外，注意到A(V)是一个n/2阶的零矩阵,则

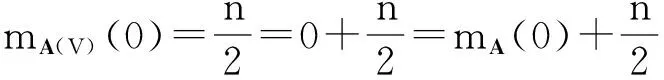
即V是矩阵A的一个P-集，这表明PS(A)≥n/2．最后，由引理1可得PS(A)=n/2，即条件(a)成立．

注1当G为具有n个点的树时，文献[6]33-34给出了S(G)中存在树矩阵A使得PS(A)=n/2的充要条件．现在，定理3将该特征刻画从树矩阵推广到所有实对称阵，完全地刻画出所有满足PS(A)=n/2的n阶实对称阵A的伴随图．

下面给出1个例子来阐明定理3给出的特征刻画．

设图G如图1所示，且有矩阵

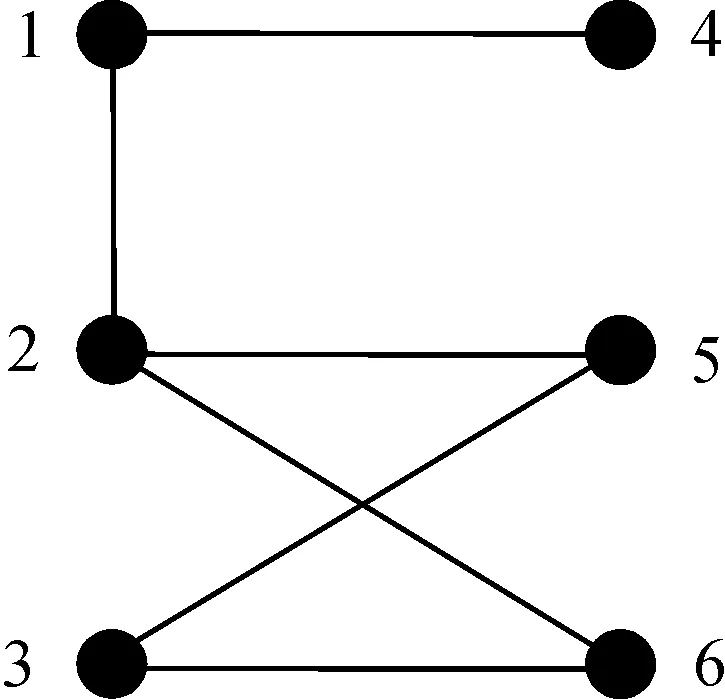
图1　图G

设G为具有n个点的图．当n为奇数时，定理2给出了S(G)中存在实对称阵A使得PS(A)=(n-1)/2的一个必要条件．结合树矩阵的相关结果[6]36，有下述猜想：

推想1设G为具有n个点的图，其中n为奇数．下述2个条件是等价的：

(a) S(G)中存在实对称阵A，使得PS(A)=(n-1)/2；

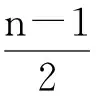
参考文献：

[1]HORNRA,JOHNSONCR.Matrixanalysis[M]. 2nded.NewYork:CambridgeUniversityPress, 2013.

[2]JOHNSONCR,DUARTEAL,SAIAGOCM.TheParter-Wienertheorem:refinementandgeneralization[J].SIAMJournalonMatrixAnalysis&Applications, 2003, 25(2):352-361.

[3]FERNANDESR,DACRUZHF.SetsofParterverticeswhicharePartersets[J].LinearAlgebraandItsApplications, 2014, 448:37-54.

[4]NELSONCG,SHADERBL.AllpairssufficeforaP-set[J].LinearAlgebraandItsApplications, 2015, 475:114-118.

[5]KIMIJ,SHADERBL.Non-singularacyclicmatrices[J].LinearandMultilinearAlgebra, 2009, 57(4).

[6]DUZ,DAFONSECACM.TheacyclicmatriceswithaP-setofmaximumsize[J].LinearAlgebraandItsApplications, 2014, 468:27-37.

【中文责编：庄晓琼英文责编：肖菁】

The Real Symmetric Matrices with a P-set of Maximum Size and Their Associated Graphs

DU Zhibin*

(School of Mathematics and Statistics, Zhaoqing University, Zhaoqing 526061, China)

Abstract：The concept of P-set of real symmetric matrices is proposed based on the multiplicity of eigenvalues of matrices and Cauchy interlacing theory. Suppose that A is a real symmetric matrix of ordern. LetmA(0) be the multiplicity of eigenvalue 0 of A, and let A(S) be the principal submatrix of A obtained from A by deleting thei1,i2,…,ikrows and columns, whereS={i1,i2,…,ik} is a nonempty subset of {1,2,…,n}. In particular, whenmA(S)(0)=mA(0)+|S|, thenSis a P-set of A. LetPS(A) be the maximum size among the P-sets of A. Based on the fact that every real symmetric matrix of ordernhas at most ⎣n/2」 elements, the structure and characteristics of the real symmetric matrices of ordernsatisfiedPS(A)=⎣n/2」 are studied; their corresponding properties are presented; the associated graphs whennis even is characterized; the associated graphs whennis odd is conjectured, which improve the results on the acyclic matrices with a P-set of maximum size.

Key words：real symmetric matrices; associated graphs; multiplicity of eigenvalues; P-set

收稿日期：2015-04-24《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

基金项目：国家自然科学基金项目(11426199)；广东省自然科学基金项目(2014A030310277)；广东省教育厅青年创新人才项目(2014KQNCX224)

*通讯作者:杜志斌，讲师，Email:zhibindu@126.com.

中图分类号：O157.5

文献标志码：A

文章编号:1000-5463(2016)01-0119-04