等离子体纳米结构Fano谐振的Q值计算研究

胡治朋， 刘　芬， 刘　柳, 张　渊

(华南师范大学华南先进光电子研究院，光及电磁波研究中心，广州 510006)



等离子体纳米结构Fano谐振的Q值计算研究

胡治朋， 刘芬， 刘柳, 张渊*

(华南师范大学华南先进光电子研究院，光及电磁波研究中心，广州 510006)

摘要：品质因子(Q值)是谐振模式电磁存储能力的一个重要评价指标，文中从定义出发得到了Q值的时域拟合公式，并结合时域有限差分方法对典型金属纳米结构以及Fano谐振各特征模式的Q值展开研究；此外，用较为简单方便的频域半高宽公式对上述结构进行了Q值计算. 通过对比2种方法得到的结果，发现尽管频域半高宽公式能够适用于简单的金属纳米结构谐振模式Q值计算，但在处理Fano谐振的Q值时将会带来较大的误差，有时甚至极大地偏离实际值导致计算结果失去意义. 文中采用的时域拟合Q值公式从谐振模式的本质出发，不受结构响应谱线型的影响，适用于各种情况下对谐振模式Q值的准确计算.

关键词：Q值; 金属纳米结构; 表面等离子体光子学; Fano谐振

Fano共振现象是FANO[1]在研究原子自电离现象时发现的. Fano共振的响应曲线与典型的Lorentz共振线型相差很大，因而这类共振模式有很多独特之处. 随着研究的深入，发现很多物理系统中都存在Fano共振现象，尤其在一些较复杂的金属纳米结构的光学响应谱中都可以观察到Fano共振的存在. 这类非对称的Fano共振模式因其独特的光学性质，近几年来受到了广泛的关注和研究，其应用领域也逐渐扩大，如基于Fano共振的纳米激光器[2]、光开关[3]、光传感[4-7]、等离子尺[8]、表面增强拉曼散射[9-10]等. 金属纳米结构的Fano共振是由于其结构中存在不同的表面等离子体共振模式之间的相互耦合形成的. 根据表面等离子纳米结构各种共振模式的远场光学特性，可以将其划分为辐射模式(一些文献中称为亮模式，Bright mode)，和非辐射模式(暗模式，Dark mode). 辐射模式可以与远场波产生作用，因此很容易通过远场激发或观测；而非辐射模式则不容易与远场入射平面波发生相互作用.

结构上的非对称性是一种较常采用的产生Fano谐振的方式， 如非对称的壳-核结构[11]、非对称盘-环结构[12-13]、纳米颗粒聚合体[14]、堆叠的环孔结构[15]、石架型结构[16]以及非对称的二量体纳米对[17-18]等. 对于这类对称性破缺结构开展了较多的理论和实验研究，主要集中在其光谱响应、电场增强等方面. 但就本质而言，表面等离子体纳米结构中的Fano谐振也是一类特殊的光学谐振器，因而其作为谐振器最重要的参数之一——品质因子(Quality factor,或Qfactor)也应该被详细研究，但目前这些方面的讨论并不多. 本文将利用时域方法对一类非对称的金属纳米结构中存在的Fano谐振的Q值展开研究，并与通常所使用的频域半高宽Q值计算公式得到的结果进行比较.

1基本理论

通常计算普通谐振器Q值表示为

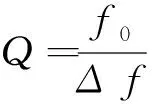
(1)

其中,f0为谐振中心频率，Δf为半高宽，本文中将式(1)简称为频域半高宽公式. 然而纳米结构的光谱响应是复杂多变的，因此有必要从谐振器Q值的原始定义进行分析.Q值的原始定义为：

(2)

根据坡印廷理论推导出色散表面等离子体纳米结构所存储的电场能[19],进而可以得到时间平均的吸收功率〈Pabs〉、辐射功率〈Prad〉及总能量〈Utotal〉的表达式：

〈Pabs〉=βabse-αt,〈Prad〉=βrade-αt，

(3)

(4)

其中，α为能量衰减系数,t为时间.通过对比式(3)和式(4)中的衰减系数α，得到时域的Q值计算式：

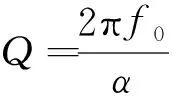
(5)其中α为能量衰减系数.根据式(3)～(5)，通过拟合纳米结构时间平均的辐射功率或吸收功率随时间变化的自然指数衰减曲线，即可求得α,从而得到Q值. 通过上述从Q值原始定义发展来的方法计算得到的谐振器Q值，对各种谐振情况都是有效且准确的.

2计算与讨论

通过考察比较几种典型的金属纳米结构(纳米棒、偶极子光学天线(optical antenna)、平行纳米棒对)及非对称的Fano谐振结构的Q值，比较时域和频域Q值计算方法的差异.

2.1典型金属纳米结构的响应谱和Q值

图1为几种基于金属纳米棒的结构，由于结构对称性高，其产生的局域等离子体谐振峰较为明确且具有典型性，因此以这些基本结构作为后面讨论Fano谐振的对比计算. 本文讨论的金属纳米结构均由横截面为50 nm×50 nm正方形的银纳米棒组成，银的材料参数(介电常数值)取自参考文献[20]，结构的其他几何特征参数由各图中插图所示. 为进一步明确所研究的问题，计算中未包括介质基底，金属结构置于空气环境中. 所有计算中平面波入射方向均垂直纸面向里，电场方向与纳米条平行(图1A). 采用时域有限差分(FDTD)方法，可以计算得到各不同纳米结构的消光谱曲线.

图1A～C为对应不同类型的金属纳米结构的消光谱线，可以看到所示结构由于对称性很高，在远场平面波的激发下只能得到一个亮模式(约300 THz处). 而图1D中所示为长度不同的“二”字型平行纳米棒对，由于在偏振方向上下2根纳米棒长度有少许差别，这种对称性的缺失会形成比较明显的Fano谐振响应线型[1]. 如图1D的谱线所示，它有3个谐振模式(M1、M2和M3)，其中M1、M3这2个峰为辐射模式即亮模式，分别在频率255 THz和320 THz处，而谷M2为非辐射模式即暗模式，位于两峰之间268 THz处.

从Q值的定义出发，利用式(5)计算出每种结构准确的Q值，如表1中时域对应数据列所示. 由计算结果可以看出，图1A～C中单一亮模式的Q值普遍较小，意味着其结构中存储电磁能量的能力比较弱，能量更容易耗散出去(通过辐射和结构的吸收). 而对于具有Fano共振的“二”字型结构(图1D)，其模式的Q值要大不少，特别是模式M1(左边亮模式)与模式M2(暗模式)的Q值要比图1A～C中单一亮模式的Q值高出2～3倍，意味着Fano共振模式下对光能的束缚能力更强大，正是Fano共振结构在纳米激光器、传感器等领域具有潜力的主要原因之一. 而模式M3(右边的亮模式)的Q值较低，与图A～C单一模式的值相当，是由于该峰的位置离Fano曲线中谷的位置较远，表明其模式之间的相互干涉耦合作用较小，仍旧保持着单个纳米棒本征谐振峰类似的光学响应.

2.2频域半高宽法与时域拟合算法计算Q值比较

在频域里，结构的Q值可通过式(1)计算得到，在本文简称为半高宽法，该方法是较常用的快速计算谐振器Q值的方式，因计算简便易行，无论是在仿真计算还是在实验测量里都有广泛的运用.

图1A～C中所示结构的光谱是比较常见的典型单峰谱线，它们的半高宽如图中位于峰值一半处的箭头所示，因此可以直接使用半高宽法得到Q值(表1). 但对于图1D中所示结构，由于模式耦合形成的Fano共振的存在，消光谱具有3个特征谐振模式(M1、M2、M3). 对于模式M1和M3，还可以利用频域Q值计算式(1)通过获取其半高宽(Δf1和Δf3)和中心频率来得到Q值，而对于Fano谷处对应的暗态模式M2，则利用频域公式来计算其Q值则将显得较为不确定. 由于2个亮模式峰值高低不等，因此在半高宽的选择上存在疑问，接下来的分析中，可以看到，由于半高宽选择方式的变化，将最终导致频域计算得到的Q值不准确. 由于Fano线形的不对称性，在用频域法计算其暗态模式时，有些研究者就采用如图1D下方插图里的方式去界定Fano谷的半高宽[21]，其半高宽Δf2取自较矮的那个亮模式M1和Fano谷M2之间的位置，即(R1+R2)/2处，最终计算出Q值，结果见表1.

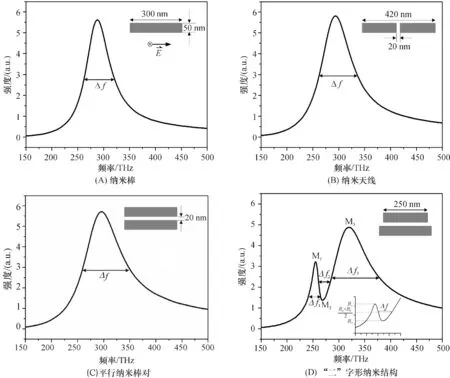
图1　不同金属纳米结构的消光光谱

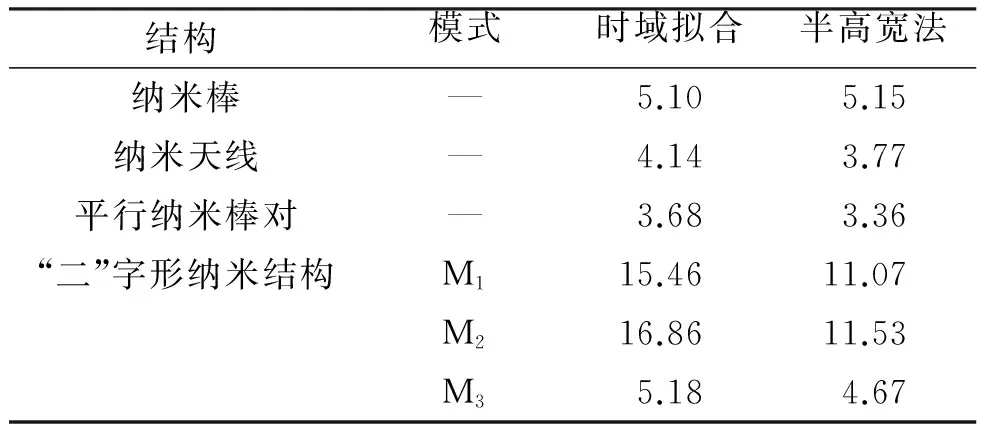
结构模式时域拟合半高宽法纳米棒—5.105.15纳米天线—4.143.77平行纳米棒对—3.683.36“二”字形纳米结构M115.4611.07M216.8611.53M35.184.67

通过对比时域拟合方法和频域半高宽法得到的Q值可以看出，对图1A～C中的纳米结构用2种方法得到的Q值是基本一致的. 然而，对图1D的Fano谐振结构，其Q值频域结果与时域计算结果相差较大，其中模式M1和模式M2的Q值差异达到30%左右，而模式M3更多地保持了单个纳米棒的谐振特性，因而2种方法计算结果差异在10%左右. 由于时域拟合方法是直接从Q值原始定义而来，其计算结果更符合实际情况，因此可以知道用半高宽法去处理Fano共振的Q值是不太准确的. Fano谐振是由不同谐振间的耦合产生的，因此其响应谱是由模式干涉叠加而成，导致其消光谱线型的非对称性比较大，特别是暗模式没有明确的半高宽，直接削弱了半高宽Q值计算公式的适用性.

Fano谐振的谱线形状随着结构参数变化(直接导致各模式间耦合情况的变化)呈现出多样化特点，有些情况下通过频域公式得到的Q值会完全偏离实际情况. 图2所示是一个由2个中间连接起来的金属纳米棒组成的“工”字结构，中间连接的金属部分长度为100 nm，其他参数与图1D中的结构一致. 该“工”字结构的光学响应谱线与图1D中的“二”字型光学响应谱有所不同，其左边亮模式M1的峰值高于右边的，其原因是中间连接部分的存在使模式间的耦合情况发生了明显的变化. 当用式(1)计算这个结构的Q值时，发现右边亮模式M3峰值的一半小于Fano谷M2的值(图中用虚线)，就意味着这一模式的半高宽无法获得，因此Q值也就无法从消光谱中获得. 而利用式(5)的时域拟合方法则不受此限制，3个特征谐振模式的Q值都能准确计算出来. 表2中列出了这个“工”字型结构分别采用式(1)和式(5)计算的Q值结果. 从结果看出，模式M1的频域计算值与时域拟合值比较接近，误差约为13%，而暗模式的结果相差巨大，误差已超过到70%(由于式(5)对各种情况均为适用的，因此以该方法计算结果为Q值的准确值)，基本可以认为用频域半高宽公式得到的这个Q值结果是不正确的.

图2　 “工”字形纳米结构及其消光光谱

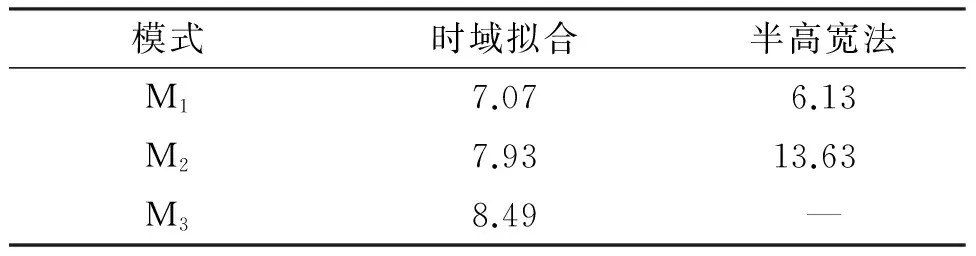
模式时域拟合半高宽法M17.076.13M27.9313.63M38.49—

通过比较表1和表2中不同方法得到的金属纳米结构Q值可知，当谐振峰谱线比较简单(近似Lorentz型)时，可以通过式(1)从结构的光学响应谱来直接计算出Q值，该方法较为简单快速. 由于金属损耗较大以及FDTD算法的网格误差等因素，时域拟合得出的金属结构谐振峰处Q值与频域半高宽法得到的结果间存在一定差别，但差别较小，基本在10%以内. 但是当用2种计算方法处理Fano谐振时，得到的结果差异很大，这种差异已经远远超出了由于金属损耗和网格划分等固有计算误差的范围，可以认为处理Fano谐振时，频域半高宽法存在严重的不足，需要谨慎使用. 遇到这种情况，应该通过式(5)来计算所设计的Fano特征谐振峰处的Q值，这样才能正确地反映所设计结构对电磁能量的实际储存能力.

3结论

本文通过时域拟合和频域半高宽2种计算方法计算了多种金属纳米结构在谐振位置处的Q值. 通过对比，发现当纳米结构的谐振模式比较简单(单一谐振峰)时，通常所用的频域半高宽法能够快速准确地得到谐振模式的Q值，但当纳米结构较复杂，出现Fano谐振时，频域半高宽法得到的Q值并不准确(有些情况下偏差很大，如本文中某些情况偏差超过70%)，导致计算结果失去实际意义.综上所述，在计算金属纳米结构Fano谐振的Q值时需避免采用频域半高宽法，而应采用FDTD算法结合时域拟合公式来计算Q值的方法；这一方法从Q值定义出发，不受纳米结构响应谱曲线形状的约束，无论对简单谐振还是复杂的Fano谐振都可以得到准确的Q值计算结果.

参考文献：

[1]FANO U. Effects of configuration interaction on intensities and phase shifts[J]. Physical Review, 1961, 124(6): 1866-1878.

[2]ZHELUDEV N I, PROSVIRNIN S L, PAPASIMAKIS N. Lasing spaser[J]. Nature Photonics, 2008, 2: 351-354.

[3]CHANG W S, LASSITER J B, SWANGLAP P, et al. A plasmonic Fano switch[J]. Nano Letters, 2012, 12(9): 4977-4982.

[4]GALLINET B, MARTINO J F . Refractive index sensing with subradiant modes: a framework to reduce losses in plasmonic nanostructures[J]. ACS Nano, 2013, 7(8): 6978-6987.

[5] ZHANG S, BAO K, HALAS N J, et al. Substrate-induced Fano resonances of a plasmonic nanocube: a route to increased-sensitivity localized surface plasmon resonance sensors revealed[J]. Nano Letters, 2011, 11(4): 1657-1663.

[6]WU C H, KHANIKAEV A B, ADATO R, et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers[J]. Nature Materials, 2011, 11(1): 69-75.

[7]CETIN A E, ALTUG H . Fano resonant ring/disk plasmonic nanocavities on conducting substrates for advanced biosensing[J]. ACS Nano, 2012, 6(11): 9989-9995.

[8]LIU N, HENTSCHEL M, WEISS T, et al. Three-dimensional plasmon rulers[J]. Science, 2011, 332: 1407-1410.

[9]YE J, WEN F, SOBHANI H, et al. Plasmonic nanoclusters: near field properties of the Fano resonance interrogated with sers[J]. Nano Letters, 2012, 12: 1660-1667.

[10]FRANCESCATO Y, GIANNINI V, MAIER S A . Plasmonic systems unveiled by Fano resonances[J]. ACS Nano, 2012, 6(2): 1830-1838.

[11]MUKHERJEE S, SOBHANI H, LASSITER J B, et al. Fanoshells: nanoparticles with built-in Fano resonances[J] Nano Letters, 2010, 10(7): 2694-2701.

[12]SONNEFRAUD Y, VERELLEN N, SOBHANI H, et al. Experimental realization of subradiant, superradiant, and Fano resonances in ring/disk plasmonic nanocavities[J]. ACS Nano, 2010, 4(3): 1664-1670.

[13]HAO F, NORDLANDER P, SONNEFRAUD Y, et al. Tunability of subradiant dipolar and Fano-type plasmon resonances in metallic ring/disk cavities: implications for nanoscale optical sensing[J]. Acs Nano, 2009, 3(3): 643-652.

[14]FAN J A, BAO K, WU C, et al. Fano-like interference in self-assembled plasmonic quadrumer clusters[J]. Nano Letters, 2010, 10(11): 4680-4685.

[15]LIU H, WANG N, LIU Y, et al. Light transmission properties of double-overlapped annular apertures[J]. Optics Letters, 2011, 36(3): 385-387.

[16]VERELLEN N, SONNEFRAUD Y, SOBHANI H, et al. Fano resonances in individual coherent plasmonic nanocavities[J]. Nano Letters, 2009, 9(4): 1663-1667.

[17]YANG Z J, ZHANG Z S,ZHANG L H, et al. Fano resonances in dipole-quadrupole plasmon coupling nanorod dimers[J]. Optics Letters, 2011, 36(9): 1542-1544.

[18]WANG J, LIU X, LI L, et al. Huge electric field enhancement and highly sensitive sensing based on the Fano resonance effect in an asymmetric nanorod pair[J]. Journal of Optics, 2013, 15(10): 105003.

[19]NI C Y A, CHANG S W, CHUANG S L, et al. Quality factor of a nanobowtie antenna[J]. Lightwave Technology, 2011, 29(20): 3107-3114.

[20]PALIK E D. Handbook of optical constants of solids[M]. Orlando, FL, USA: Academic Press, 1985: 353-357.

[21]SHEN Y, ZHOU J, LIU T, et al. Plasmonic gold mushroom arrays with refractive index sensing figures of merit approaching the theoretical limit[J]. Nature Communications, 2013, 4: 2381.

【中文责编：成文英文责编：李海航】

The Study of Quality Factor Calculation of Fano Resonance in Plasmonic Nanostructures

HU Zhipeng， LIU Fen， LIU Liu, ZHANG Yuan*

(Centre for Optical and Electromagnetic Research, South China Academy of Advanced Optoelectronics,South China Normal University, Guangzhou 510006, China)

Abstract：Fano resonance in plasmonic nanostructures has been attracted more and more attentions because of its special optical properties and application potential. Quality factor (Qfactor) is very important to evaluate the ability of electromagnetic energy storage of a resonator. In this paper, the fitting formula in time domain is firstly got from the original definition of theQfactor; based on this formula and combining with FDTD method, theQfactors of typical resonance of several plasmonic nanostructures (including metallic nanorod，nano-antenna and one sample showing evident Fano resonance) is calculated. Besides, theQfactor is also calculated by using the common frequency method (the FWHM formula). By comparing calculation results from the two method above, it is found that the FWHM formula is not suitable (sometimes incorrect) when dealing with theQfactor of Fano resonance, although it could be accuracy enough and fast when treating simple plasmonic resonance with single peak; while theQfactor fitting formula from FDTD method could be used for all type of plasmonic resonance (including Fano resonance) because of its direct origin from the definition ofQfactor.

Key words：Qfactor; metallic nanostructure; plasmonics; Fano resonance

收稿日期：2016-01-10 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

基金项目：国家自然科学基金项目(61108022)；广东省自然科学基金项目(201001D0104799318)

*通讯作者:张渊，副教授，Email: yuan.zhang@coer-scnu.org.

中图分类号：O436.2

文献标志码：A

文章编号:1000-5463(2016)01-0047-05