基于响应面法的齿轮容差设计方法研究

王桂华，井海龙，史妍妍，陈云霞（.中航工业沈阳发动机设计研究所，沈阳005；.北京航空航天大学可靠性与系统工程学院，北京009）



基于响应面法的齿轮容差设计方法研究

王桂华1，井海龙2，史妍妍1，陈云霞2
（1.中航工业沈阳发动机设计研究所，沈阳110015；2.北京航空航天大学可靠性与系统工程学院，北京100191）

摘要：随着附件传动系统不断向高速、重载方向发展，齿面接触可靠性问题越来越受关注。为提高齿轮可靠性，分析了齿轮传动系统常见误差类型及影响，开展了齿轮容差设计初步探讨。根据齿轮制造、加工及系统动态误差的产生原理和作用方式，基于齿轮接触应力仿真结果，确定了影响齿轮接触应力随机性的5种主要误差形式及其特征量分布规律，提出了基于响应面法的齿轮容差设计方法，给出了齿轮系统公差设计的改进方向：在进行齿轮公差设计时，重点控制H、V方向的轴向平行度公差。

关键词：齿轮；容差设计；可靠性；接触应力；随机性；响应面；传动系统；敏感性分析

引用格式：王桂华，井海龙，史妍妍，等.基于响应面法的齿轮容差设计方法研究[J].航空发动机，2016,42（3）1-6.WANG Guihua，JING Hailong，SHI Yanyan,et al.Methods of tolerance design for gears based on response surface methodology[J].Aeroengine，2016,42（3）：1-6.

0　引言

随着航空发动机推重比不断提高，附件传动系统逐渐向高速、重载方向发展，越发严苛的工作条件也对传动齿轮提出了更高的可靠性要求[1]。在航空发动机维修过程中发现，80%以上的齿轮失效是齿面接触疲劳造成的[2]。因此，研究齿轮的齿面接触应力可靠性，对提高附件传动系统及发动机整体工作的可靠性意义重大。

齿轮的工作可靠性受到多种随机因素的综合作用，其中制造、加工及系统动态误差的存在是随机性产生的主要原因。文献[3]针对不同轴线平行度偏差对某附件机匣传动系统轴系结构的影响进行对比仿真分析；文献[4]建立了带有安装与制造误差的齿轮参数化模型，并对其进行动态仿真，得到齿轮在安装与制造误差影响下的动态接触应力；文献[5]针对斜齿轮进行建模及仿真，分析了齿轮在齿侧间隙误差和轴平行度误差下力学性能的变化；文献[6]得到了齿形误差及公差对齿轮振动的影响。

以上研究仅针对单一误差对齿轮传动系统齿轮性能的影响做了分析，而对于多种误差协同作用对齿轮性能的影响，及每种误差因素的影响程度，并没有给出明确的结论。

本文根据齿轮制造、加工及系统动态误差的产生原理和作用方式，确定了影响齿轮接触应力随机性的5种主要误差形式及其特征量分布规律，提出了基于响应面方法的齿轮公差设计方法，并给出了齿轮系统公差设计的改进方向。

1　齿面接触应力随机性模型的构建

1.1齿轮加工误差的影响分析

受到机床加工精度等客观因素的限制，在齿轮加工过程中不可避免会存在一定的误差。根据对齿轮传动性能的影响，归纳为主要影响传递运动准确性、传动平稳性和载荷分布均匀性的3组误差项。其中，影响齿面接触应力可靠性的主要是第2、3组，见表1。

1.2齿轮装配误差的影响分析

发动机附件机匣通常采用多平行轴齿轮传动系统，装配中主要存在以下2类误差：

（1）中心距偏差（Δfa）。是指在齿轮副的齿宽中间平面内，实际中心距与公称中心距之差。

（2）轴线平行度误差。是指1对齿轮的轴线分别在2个基准平面上投影的平行度误差（在等于齿宽的长度上测量），具体分为轴线平面内的偏差（fΣδ）和垂直平面上的偏差（fΣβ），简称H、V方向的轴线平行度误差。具体形式如图1所示。

表1 影响齿面接触应力的加工误差

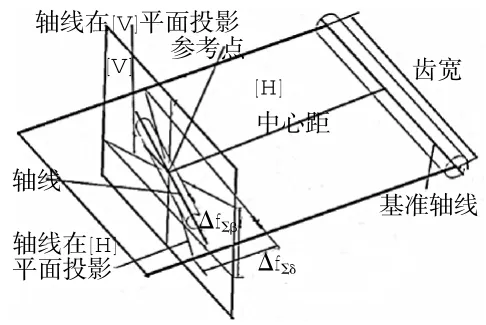
图1 齿轮系统装配误差[7]

1.3齿轮系统动态误差的影响分析

齿轮系统动态误差是指齿轮系统受到温度、振动和工作载荷等综合作用时，由其装配环境的变化引起的误差类型。该类误差一般与齿轮装配误差相互耦合，可以累加入装配误差之中。

本文主要针对影响齿轮接触应力的误差类型进行研究，根据每类误差的形成原理和作用方法，结合工程经验，筛选出影响齿轮接触应力的2类加工误差和3类装配误差，如图2所示。

根据齿轮产品在机械加工装配过程中各设计参数分布的特性，结合齿轮传动系统的实际设计资料，以附件机匣1对齿轮为例，得到了其5类误差参数，见表2。

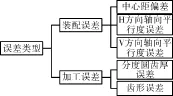
图2 影响齿轮接触应力的误差类型

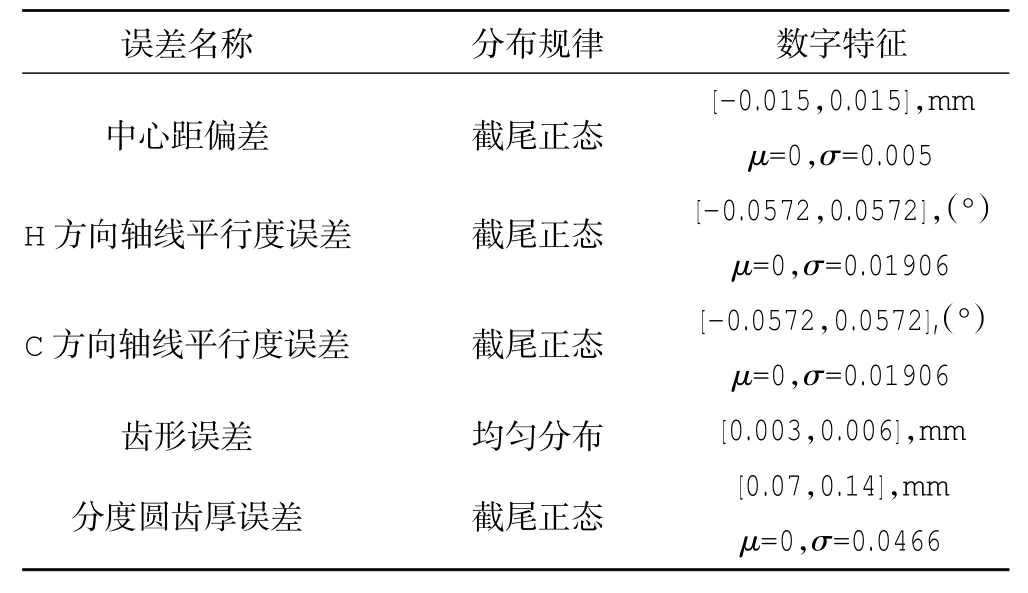
表2 齿轮公差信息

1.4构建误差齿轮模型

本文在标准齿轮副应力仿真的基础上，考虑齿轮存在的误差类型，根据各类误差的定义或常见形式，将其直接或间接转化后加入到常规标准齿轮副中形成齿轮误差模型，进行基于有限元的误差齿轮应力仿真。

根据定义，构造齿轮副中心距偏差和轴线平行度误差，如图3、4所示；将分度圆齿厚误差转换成齿轮某1齿面的偏置，如图5所示；在齿轮实际生产制造中，多数齿形误差为中凹型，且齿形误差一般处于齿面中部，所占齿面面积约为1/2，因此，针对齿轮模型构造中凹齿形误差轮齿，如图6所示。

图3 中心距偏差建模

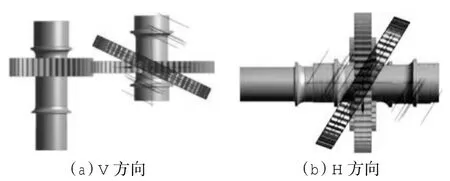
图4 轴线平行度误差

1.5误差齿轮的接触应力仿真分析

采用有限元方法进行上述5种误差因素协同作用下的齿轮接触应力仿真分析。根据表2确定的误差分布规律，随机抽样确定有限元仿真的误差参数组合，同时利用有限元瞬态动力学仿真确定最大应力出现的相位，从而建立处于最大应力相位的齿轮误差模型，进而采用有限元静力学仿真进行基于齿轮误差模型的应力仿真分析。具体流程如图7所示。

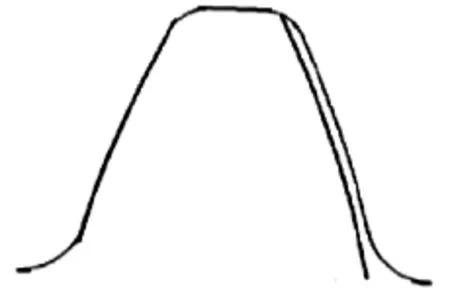
图5 分度圆齿厚误差

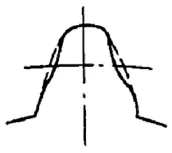
图6 齿形误差

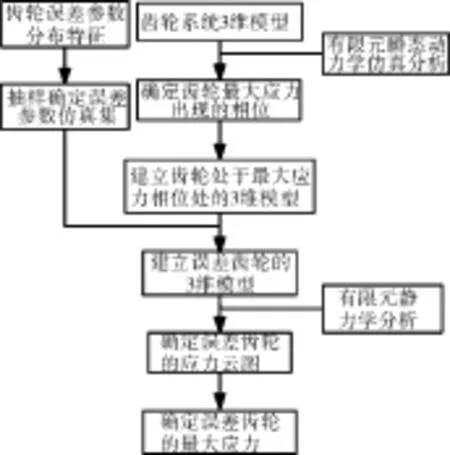
图7 基于误差的齿轮应力仿真流程

2　基于响应面的齿轮系统公差设计

2.1基本原理

基于响应面的齿轮公差设计，首先根据齿轮误差参数的分布类型进行抽样，确定误差参数仿真集，利用误差齿轮的接触应力仿真分析方法确定误差参数及对应的齿轮接触应力大小，根据抽样样本及对应的应力仿真结果建立齿轮系统应力与误差参数的响应面模型；其次根据响应面模型进行误差参数敏感性分析，确定其每种误差参数的敏感性及单因素条件下的最坏情况，再进行综合误差因素最坏情况分析，确定综合误差因素下的最大应力，若2种最坏情况的最大应力任何1个不满足要求，则计算其可靠度，若可靠度不满足要求，则需找出最坏参数组合，进而根据单因素敏感性分析结果进行参数的优化设计，具体流程如图8所示。

2.2齿轮系统接触应力响应面模型构建

响应面法[8]的基本原理是：首先假设1个包含未知系数的、由状态变量与基本变量构成的解析表达式，然后用拟合的方法确定未知系数以表达隐式函数或高度非线性函数。多项式系数的确定一般以试验设计为基础，应用正交设计或均匀设计回归得到特定因子的最小二乘估计。采用该方法时，随机变量的个数越多，试验次数便越多。

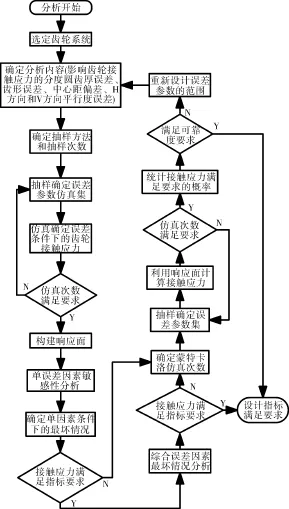
图8 基于响应面的齿轮系统公差设计

在结构力学分析领域，响应面函数模型常采用2阶多项式形式[9]

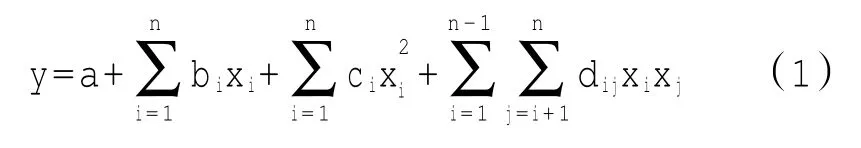
式中：a、bi、ci、di为待定系数；xi和xj（i=1,2,…,n;j=1,2,…，n-1）为基本变量。

由于齿轮误差种类较多且具有截尾分布的特点，在保证抽样结果合理性的同时，考虑仿真分析的效率。本文采用超拉丁立方[10]抽样得到80次仿真的样本值，建立齿轮系统试验误差组合集，并进行误差齿轮的接触应力仿真分析。

利用前70组数据进行响应面建模，后10组数据进行响应面模型的验证。利用完全2阶多项式对前70组数据拟合得到接触应力的响应面模型

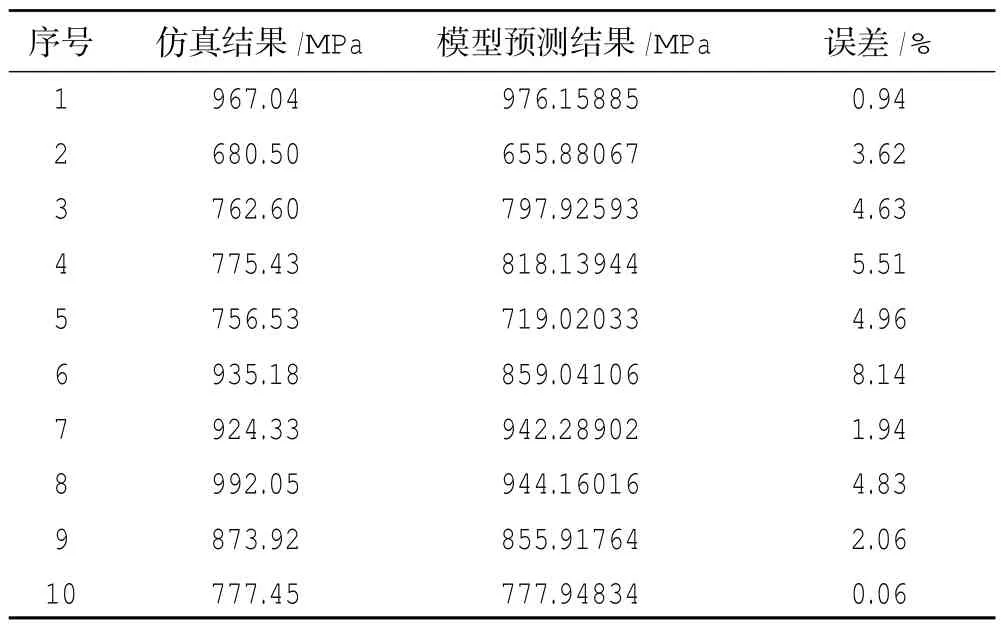
表3 响应面模型验证结果

式中：σ为接触应力；X11为分度圆齿厚误差，单位为mm；X1为有限元仿真输入参数，反映了分度圆齿厚误差，单位为mm；X2为齿形误差，单位为mm；X3为中心距偏差，单位为mm；X4为H方向轴向平行度误差，单位为°；X5为V方向轴向平行度误差，单位为°。

利用后10组数据进行接触应力模型的验证，验证结果见表3。

从表中可见，齿轮系统接触应力响应面模型预测结果与仿真分析结果误差在10%以内，认为模型可以作为后续分析的依据。

利用协方差矩阵进行贡献率分析，得到分度圆齿厚误差、齿形误差、中心距偏差和H、V方向轴向平行度误差这5种误差参数对应力分析结果的贡献率[11]分别为26.5874%、22.8871%、20.8440%、18.2140%和11.4675%。

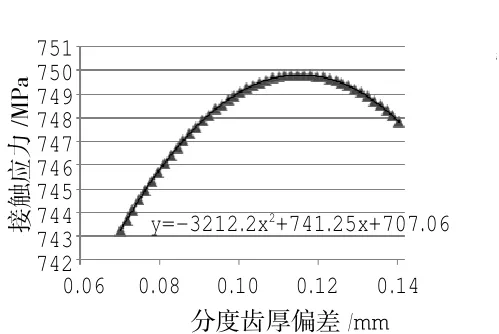
图9 齿厚误差敏感性分析结果

2.3误差参数敏感性分析

敏感性分析是指从定量分析的角度研究有关因素发生某种变化对某1个或1组关键指标影响程度的1种不确定分析技术。其实质是通过逐一改变相关变量数值来解释关键指标受这些因素变动影响大小的规律。

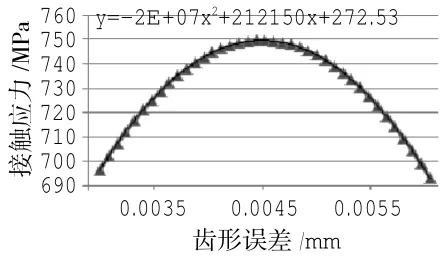
图10 齿形误差敏感性分析结果

分别将不同的齿轮误差因素设为单一变量，通过固定其它4种误差因素，对每种误差因素进行齿轮接触应力敏感性分析。

首先以齿厚误差为例，分别固定齿形误差、中心距偏差和H、V方向轴向平行度误差为均值，分析齿厚误差对齿轮系统接触应力的影响，如图9所示。

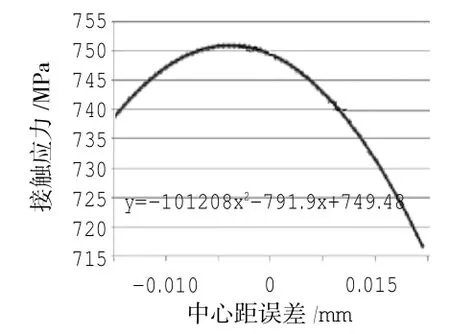
图11 中心距偏差敏感性分析结果

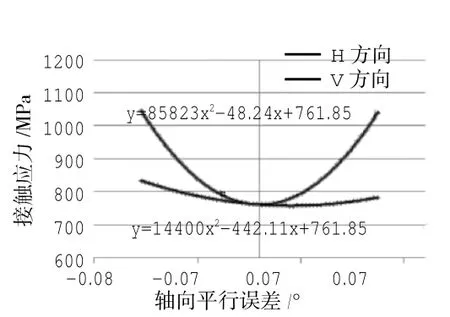
图12 轴向平行度偏差敏感性分析结果

从图中可见，在固定齿形误差、中心距偏差和H、V方向轴向平行度误差这4个误差因素的条件下，分度圆齿厚误差在[0.07，0.14]范围内变化时，齿轮的接触应力范围为[744.7，762.8]，应力幅值相对于应力均值的变化率为0.045%，变化不明显。

以此类推，得到：

（1）齿形误差在[0.003，0.006]范围内变化时，齿轮的接触应力范围为[704.7，761.9]，应力幅值相对于应力均值的变化率为4.04%，变化不明显，如图10所示。

（2）中心距偏差在[-0.015，0.015]范围内变化时，齿轮的接触应力范围为[761.1，814.5]，应力幅值相对于应力均值的变化率为3.39%，变化不明显，如图11所示。

（3）H方向轴向平行度误差在[-0.0572，0.0572]范围内变化时，齿轮的接触应力范围为[761.9，1045.4]，应力幅值相对于应力均值的变化率为15.7%，变化明显；V方向轴向平行度误差在[-0.0572，0.0572]范围内变化时，齿轮的接触应力范围为[758.5，834.2]，最大应力相对最小应力变化4.75%，变化不明显，如图12所示。

根据单误差因素敏感性分析结果，确定各误差参数的敏感性由高到低为：H方向轴向平行度误差、V方向的轴向平行度误差与齿形误差、中心距偏差和分度圆齿厚误差。因此，在进行公差设计时，应按上述敏感性从高到低考虑。

2.4综合误差因素最坏情况分析

最坏情况分析法是1种按照不常发生的最坏使用条件的组合为基础，进行确保系统可靠性要求的设计方法[12]，是1种非概率统计方法，用来分析系统的设计参数和各种内、外影响因素的参数处于最坏情况或最坏组合情况下的系统性能参数偏差。对于大规模复杂系统来说，用其分析各类参数处于最坏情况下系统的性能是否还满足指标要求，并找出导致系统性能参数处于最坏情况下的设计参数和影响因素的组合规律。

应用该方法的前提是假设各类影响因素对系统的影响是呈单调性的，即影响因素的参数取标称值时系统处于最理想状态，其参数偏离标称值越大对系统的影响也越大[13]。由敏感性分析可知，本文研究的5个误差因素只有H、V方向的轴向平行度误差对系统的影响呈现单调性。结合接触应力的响应面模型，采取仿真与数值分析相结合的方法进行最坏情况分析，H、V方向的轴向平行度误差2个参数采取上、下极限值全面组合的方法，其余3个参数采取数值分析的方法进行3参数下的最大应力分析。具体流程如图13所示。

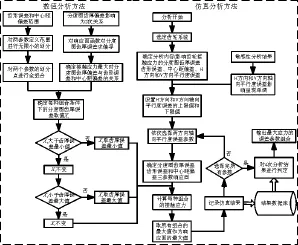
图13 综合因素最坏情况分析流程

分别对H、V方向轴向平行度误差的极限值（± 0.0572°）进行全面组合，确定分度圆齿厚误差、齿形误差和中心距偏差3参数的响应面，利用数值的方法确定其最大应力，分析结果见表4。

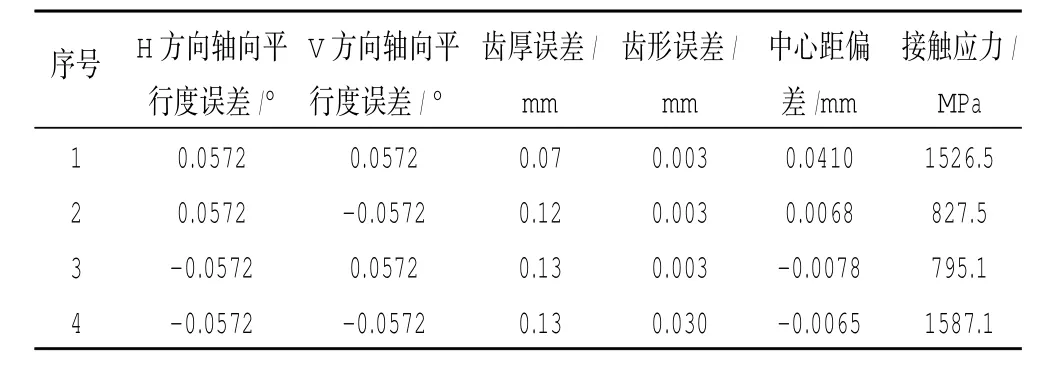
表4 综合因素最坏情况分析结果

齿轮的接触疲劳极限为1500 MPa，其设计安全系数为1.0。从表中可见，在极限1、4状态下，不满足齿轮接触应力的要求。

2.5基于响应面的齿轮系统可靠度分析

将齿轮的齿面安全系数作为可靠性分析的指标，由齿轮设计要求可知齿轮齿面的计算安全系数不能小于设计安全系数。因此，齿轮副的可靠度定义为在随机误差综合影响下齿轮副的计算安全系数不大于设计安全系数的概率，表达式如下

式中：R为齿轮副可靠度；n为齿轮齿面的计算安全系数；ns为齿面设计安全系数。齿根的安全系数定义为[14]

式中：σHlim为材料的接触疲劳极限；σH为齿轮齿面应力。

本文基于蒙特卡洛思想[15]，根据齿轮误差因素的分布特点，对其公差构成的随机变量进行大量重复抽样，将样本值带入响应面模型，确定每组误差组合的接触应力响应，得到每组误差组合下的安全系数，利用式（4）计算其可靠度为0.9923。

3　结论

本文根据齿轮制造、加工及系统动态误差的产生原理和作用方式，确定了影响齿轮接触应力随机性的5种主要误差形式及其特征量分布规律，提出了基于响应面方法的齿轮公差设计方法，并给出了齿轮系统公差设计的改进方向。

分析结果表明：影响齿轮接触应力随机性的误差主要有5种，即分度圆齿厚误差、齿形误差、中心距偏差和H、V方向轴向平行度误差。在进行齿轮公差设计时，应重点控制H、V方向的轴向平行度误差。

参考文献：

[1]林基恕.航空燃气涡轮发动机机械系统设计[M].北京：航空工业出版社，2005：157-160. LIN Jishu.Mechanical system design for aero gas turbine engines[M]. Beiijng：Aviation Industry Press，2005：157-160（.in Chinese）

[2]史妍妍.基于热分析的附件机匣若干可靠性问题研究[D].沈阳：东北大学，2009. SHI Yanyan.Study on accessory gearbox reliability based on thermal analysis[D].Shenyang：Northeastern University，2009（.in Chinese）

[3]王宇宁，孙志礼，杨丽，等.考虑装配误差的轴系结构静力学对比分析[J].中国工程机械学报，2014，12（1）：13- 17.WANG Yuning，SUN Zhili，YANG Li，et al.Statics comparative analy-sis on shafting structures with consideration of assembly error [J].Chinese Journal of Construction，2014，12（1）：13-17.（in Chinese）

[4]佟操，孙志礼，马小英，等.考虑安装与制造误差的齿轮动态接触仿真[J].东北大学学报，2014，35（7）：996-1000. TONG Cao，SUN Zhili，MA Xiaoying，et al.Dynamic simulation of spur gears with assembly errors and machining errors [J].Journal of North-eastern University（Natural Science），2014，35（7）：996-1000.（in Ch-inese）

[5]孙之星.考虑装配误差的齿轮接触应力仿真研究[D].太原：太原理工大学，2010. SUN Zhixing.Contact stress simulation study of gears with assembly error[D].Taiyuan：Taiyuan University of Technology，2010.（in Chinese）

[6]Bonori G，Pellicano F.Non-smooth dynamics of spur gears with manu-facturing errors [J]. Journal of Sound and Vibration，2007，30（6）：271-283.

[7]方昆凡.公差与配合使用手册[M].北京：机械工业出版社，2012：35-40. FANG Kunfan.Manual of tolerances and fits [M].Beijing：Machinery Industry Press，2012：35-40.（in Chinese）

[8]Chamoli S.ANN and RSM approach for modeling and optimization of designing parameters for a V down perforated baffle roughened rectan-gular channel [J]. Alexandria Engineering Journal，2015，54（3）：429-446.

[9] Myers R H，Montgomery D C，Vining G G，et al. Response surface methodology:aretrospective and literature survey[J].Journal of Quality Technology，2004，36（1）：53-77.

[10]Gangel M，Seiler M J，Collins A. Latin hypercube sampling and the identification of the foreclosure contagion threshold [J].Journal of Behavioral Finance，2013，14（2）：149-159.

[11]PianosiF，Sarrazin F，W agener T.A matlab toolbox for global sensi-tivity analysis [J]. Environmental Modeling & Software，2015，70：80-85.

[12]陈云霞，段朝阳.飞控系统最坏情况分析方法研究[J].航空学报，2005，26（5）：647-651. CHEN Yunxia，DUAN Chaoyang.Study on worst case analysis method for flight control system [J].Acta Aeronautica et Astronautica Sinica，2005，26（5）：647-651.（in Chinese）

[13]陈云霞.性能与可靠性一体化建模和分析方法研究[D].北京：北京航空航天大学，2004. CHEN Yunxia.Study on the method of integrated modeling and anal-ysis for performance and reliability [D].Beijing：Beihang University，2004.（in Chinese）

[14]孙自龙，闫凤英，刘丽.齿轮加工中剃齿的误差分析及处理[J].金属加工（冷加工），2014（5）：63-65. SUN Zilong，YAN Fengying，LIU Li.Error analysis and treatment for gear shaving during gearmachining [J].Metal W orking（Cold），2014 （5）：63-65.（in Chinese）

[15]W alter J C，Barkema G T.An introduction to Monte Carlo methods[J]. Physica A: Statistical Mechanics and Its Applications，2015，418：78-87.

（编辑：栗枢）

Methods of Tolerance Design for Gears Based on Response Surface Methodology

WANG Gui-hua1，JING Hai-long2，SHIYan-yan1，CHEN Yun-xia2
（1.AVIC Shenyang EngineDesign and Research Institute，Shenyang 10015；2.School of Reliability and Systems Engineering，Beihang University，Beijing 100191）

Abstract:With the accessory driving system takes the way towards the high speed and heavy load,the contact reliability of aviation gears make more sense. In order to improve the reliability,the common error types and effects of gear driving system were analyzed,and the study of tolerance design was proposed.According to gear rtypes and their characteristics of the random error of the contact stress of the gear were determined on the basis of the simulation results.Moreover,a method of gear tolerance design based on response surface was proposed and the improvement direction of tolerance design of gear system was given:the tolerance for the direction of H and V should be mainly controlled during the tolerance design.

Key words:gear；tolerance design；reliability；contact stress；randomness；response surface；driving system;sensitivity analysis

中图分类号：V215.1

文献标识码：A

doi：10.13477/j.cnki.aeroengine.2016.03.001

收稿日期：2015-12-30基金项目：航空动力基础研究项目资助

作者简介：王桂华（1965），女，博士，自然科学研究员，从事航空发动机强度与可靠性设计工作；E-mail：wangguih@sina.com。