压差控制器的稳定性分析和设计参数的研究

李洪胜，王　曦，王华威，党　伟，张　耿（1.中国燃气涡轮研究院，成都610500；2.先进航空发动机协同创新中心，北京100191；3.北京航空航天大学能源与动力工程学院，北京100191）



压差控制器的稳定性分析和设计参数的研究

李洪胜1,2,3，王曦2,3，王华威2,3，党伟2,3，张耿2,3
（1.中国燃气涡轮研究院，成都610500；2.先进航空发动机协同创新中心，北京100191；3.北京航空航天大学能源与动力工程学院，北京100191）

摘要：压差控制器是航空发动机燃油计量的重要部件，用于保持计量活门前后的压差恒定。为探究其控制压差能力的因素，研究了某型发动机加力系统中压差控制器的性能，分析并推导出其影响控压差能力的主要因素，并在AMESim仿真环境下对所得结果进行建模仿真，验证了所得结论的正确性。在此基础上对其进行合理的改型，为保证改型不影响系统稳定性，用小偏差原理对改型前后的压差控制器辨识，得到传递函数，确保改型并未损失其动态性能。最终得到改进压差控制器控压差能力的理论依据。

关键词：压差控制器；液压控制；稳定性；AMESim模型仿真；稳定裕度；计量活门

引用格式：李洪胜，王曦，王华威，等.压差控制器的稳定性分析和设计参数的研究[J].航空发动机，2016,42（3）：12-16.LI Hongsheng,WANG XI,WANG Huawei,et al.Differential pressure controller stability analysis and research of design parameters[J].Aeroengine,2016,42(3):12-16

0　引言

压差控制器是发动机燃油计量装置中至关重要的部分，国内的研究多是对现有型号进行仿真，通过单一变量方法逆向测试出其改型方向，其特性一般都是通过软件仿真和试验的方式获得。尚洋等[1]利用AMESim软件对压差活门的阀口直径、阀芯直径、弹簧刚度等进行了定性测试，给出压差活门的直径阀口和弹簧等参数改进的建议；康伟等[2]对发动机执行机构在EASY5框架下建模，并在静态特性仿真中得出在不同压差作用下，计量燃油量随计量形孔的变化曲线，验证了不同压差下流量变化趋势。

本文研究了某型发动机加力系统中压差控制器的性能，分析并推导出其控压差能力的影响因素，并在AMESim环境下对所得结果进行建模仿真。

1　压差控制器介绍

1.1压差控制器工作原理

压差控制器一般由压差活门与执行活门构成。压差活门感受压差变化，执行活门改变计量活门后压力。在一些小流量的压差控制器中，这2个活门一般会合二为一[3]。

根据流量公式

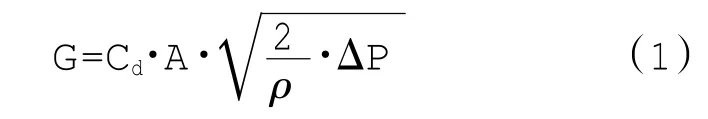
式中：Cd为流量系数；A为计量活门形孔面积；ρ为液体密度；ΔP为计量活门形孔前后压差。

由式（1）可知，若Cd、ρ和ΔP均为常数，则只需改变A的大小，G就能精确地与A呈线性变化。

某型发动机压差控制器原理如图1所示。压差活门无弹簧端作用于计量活门前油压Ps，弹簧端作用于计量活门后油压P1和弹簧力，根据两端压差进行移动，同时开大或关小高压油通往执行活门弹簧腔的阀口S0，从而控制执行活门弹簧端的油压P2，使执行活门移动，改变憋压腔出口即回油型面S1的面积[4]，控制憋压腔压力P1变化，即可保持计量活门前后油压差Ps-P1不变。

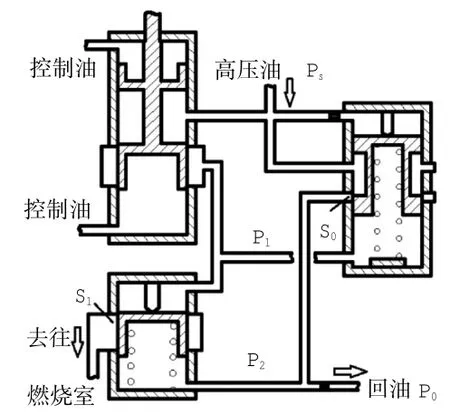
图1 某型发动机压差控制器原理

例如，计量活门前压力Ps增大时，压差活门向弹簧端移动，开大高压油通往执行活门弹簧腔的环孔面积S0，执行活门弹簧腔压力P2变大，使执行活门向无弹簧端移动，关小憋压腔出口的面积S1，憋压腔油压P1升高，计量活门前后油压差Ps-P1回落，进入另一个稳态。

1.2研究压差控制器的重要性

若计量过程中压差ΔP不稳定，就会影响G与A的线性，造成计量燃油量不准。如果发动机给油量不足，就会造成功率不足，推力不够；给油量过多，就会造成超转、超温，产生严重后果。

在发动机实际工作中，影响压差的扰动主要来自于高压油压的突然振荡、计量活门的迅速打开或关闭还有回油压力的波动等。如果压差产生波动，就会造成燃油计量不准。

所以研究压差活门的特性非常重要，确定哪些参数影响其稳态特性和动态特性，在设计压差活门时就能合理选取，保证压差控制器的性能。

2　压差活门的数学模型

2.1压差活门滑阀所受稳态液动力

液流经过阀口时，流动方向和流速的变化会造成液体动量的改变，因此阀芯上会受到附加的作用力，称为液动力[5]。在阀口开度一定的稳态流动情况下，液动力为稳态液动力，稳态液动力的方向总是使滑阀趋于关闭。

设圆形阀口开度为x，则阀口节流面积为

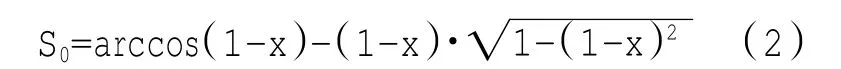
为便于计算，现将x 与S0的函数关系拟合成1条2次曲线[6]，如图2所示。

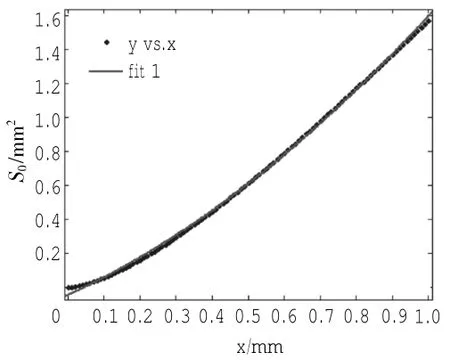
图2 阀口面积拟合曲线

则单个阀口面积随开度的关系可表示为

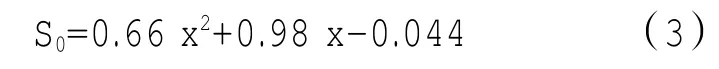
根据动量定理的计算，每个阀口处滑阀受到的稳态液动力[7]可表示为

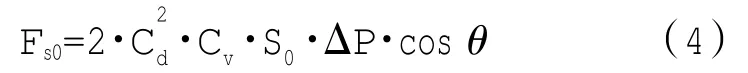
式中：取Cd=0.62；Cv为流速系数，取0.97；θ为阀口液流的射流角。

压差活门在主要工作状态中，阀口前后压差范围约为ΔP=0.58 MPa，阀口的开度约为x=0.5 mm。根据阀口射流角随阀口开度的变化关系[8]，可认为压差活门阀口在主要工作范围内的射流角均为69°。

根据以上参数可以求得滑阀受到的4个阀口处的稳态液动力为

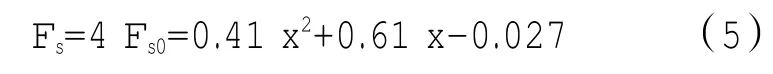
2.2压差活门滑阀的运动力学平衡方程

分析压差活门滑阀的受力[7]，滑阀上所受的外部作用力包括液压力、液动力、侧向液压力、摩擦力、弹簧力、重力、以及惯性力。

由于4个阀口为对称设计，侧向液动力相互抵消；进行稳态分析时不考虑所受瞬态液动力、摩擦力；重力相对于滑阀外部液压力非常小，可以忽略不计。

据此，列出压差活门滑阀的动力学平衡方程，即运动微分方程式，系统处于某一平衡状态时

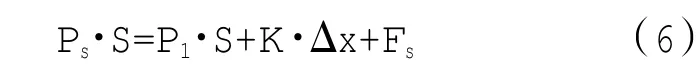
式中：P1为计量活门后压力；S为压差活门滑阀截面积；K为压差活门弹簧刚度；Δx为压差活门弹簧初始压缩量。

3　压差控制器性能分析

3.1压差变化的原因

压差控制器的作用是保证压差不变，所以首先要考虑的便是控压差这一性能。

将式（6）变形得到

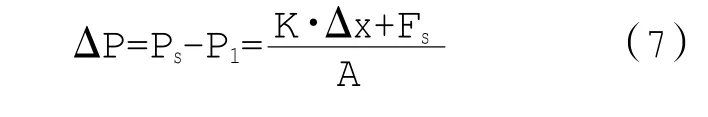
由式（7）可知，压差控制器的ΔP由弹簧力、A和Fs决定。

假设Ps增大，计量活门前后压差Ps-P1增大，压差活门阀口开度变大，使执行活门弹簧腔压力P2变大，执行活门开度变小，P1变大，Ps-P1回落，压差活门开度也随之减小，达到新的平衡状态，最终在新稳态下，阀口开度比上一个稳态略大，弹簧压缩量变大，弹簧力变大，活门受到的稳态液动力也变大，计量活门前后压差必然发生变化，即压差控制器产生了静差。

3.2静差产生原因

设Ps'为Ps的增量，P1'为P1的增量，x'为弹簧压缩量的增量，也为x的增量，可列新稳态下的阀芯受力平衡方程

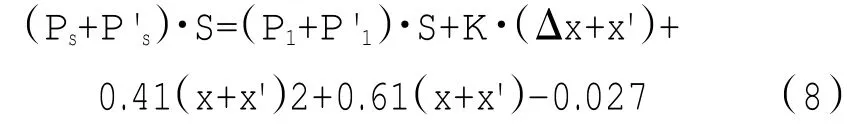
将式（6）和式（8）两边相减得到

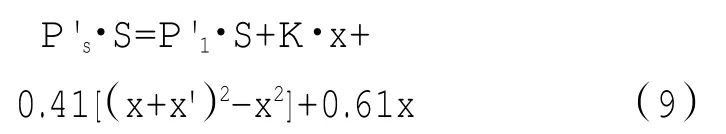
整理得到

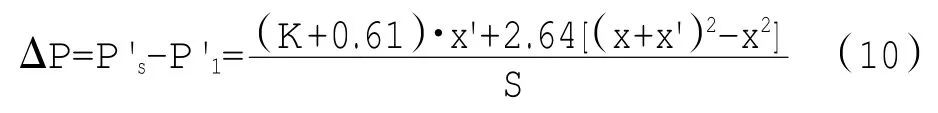
分析上式，为使压差Ps-P1不变，必须保证左端Ps'-P1'=0。压差的稳态误差来自于x'、K、x和S。由动态上分析可知，压差控制器是0型系统，利用终值定理可求出必然存在阶跃响应的稳态误差，且误差大小与开环增益K+1成反比，为减小稳态误差，需要提高开环增益，即调节上述各系数。

3.3改进压差控制器的措施

由上述分析可知，可通过以下3项措施来减小压差活门的稳态误差：增大S，即增大滑阀直径D；减小K；增加阀口的宽度，以减小x'，对于圆形阀口，即增加阀口直径d。

对于分子后半项，设

对x'1次求导后得

2次求导后得y¨=2。可知在x和x'均为正时，函数y为过原点的增函数且为凹函数，x越大斜率越大，相对的函数值y也越大，所以，另1个减小压差偏移的方法是尽量减小阀口工作时的开度x。为保证同样阀口面积的前提下减小x，即增大d，与最后1种小压差活门的稳态误差措施相同。

4　稳态分析AM ESim仿真

4.1AM ESim软件

AMESim是1款专门用于液压/机械系统建模、仿真及动力分析的优秀软件，具备图形化的仿真界面、完善的仿真类库、完整的软件接口，给航空发动机的控制系统的分析和设计带来了非常大的便利[9]。

针对3.3节中所得结论，在AMESim环境下仿真。验证结论的正确性。某型压差控制器参数见表1。

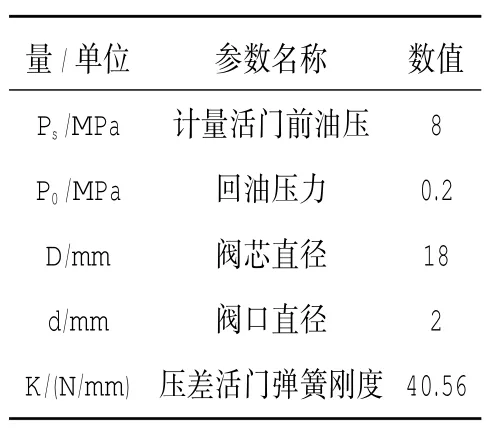
表1 某型压差控制器参数

4.2模型的建立和仿真

搭建压差控制器的AMESim模型，如图3所示。

用AMESim对3.3节中的3条措施分别仿真，得到曲线（部分），如图4~6所示。从图中可见，调节上述参数可减小压差的稳态误差。

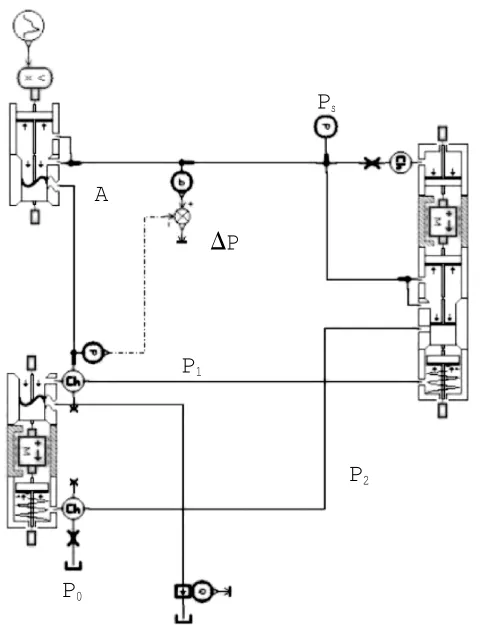
图3 阀口面积拟合曲线

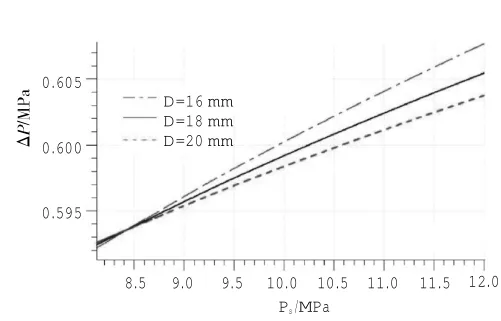
图4 不同D下，ΔP随Ps的变化曲线

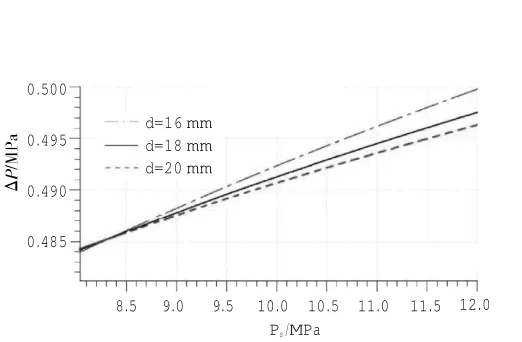
图5 不同d下，ΔP随Ps的变化曲线

5　压差控制器参数优化设计

5.1参数改进的原则

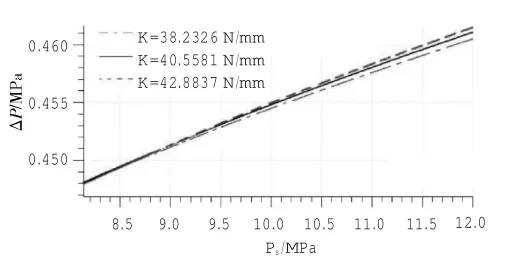
图6 不同K下，ΔP随Ps的变化曲线

在调节上述3个参数时，会存在1组最适合参数，能明显改善压差损失。定性分析参数的调节原则如下。

首先，采用单一变量原则，求出式（10）的左边分别关于D、K、d这3个参数的函数关系，定义域范围是3个参数的实际可调整范围，绘制3条函数曲线如图7所示。

从图中可见，在各参数的可调范围内，参数D对于压差影响较大，K和d对压差影响较小。

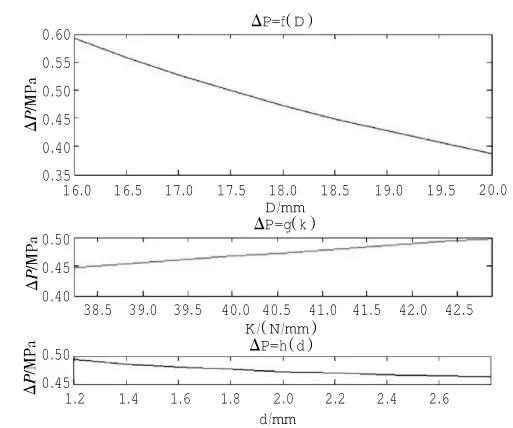
图7 参数D、K、d与ΔP的函数关系

5.2验证新压差控制器的性能

在此压差控制器基础上，对其进行改型设计，D由18 mm增大到20 mm，另外2个参数保持不变，改型前和新改型的压差控制器控压差的性能如图8~10所示。

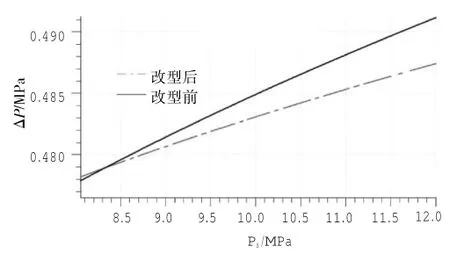
图8 改型前后压差随Ps变化情况

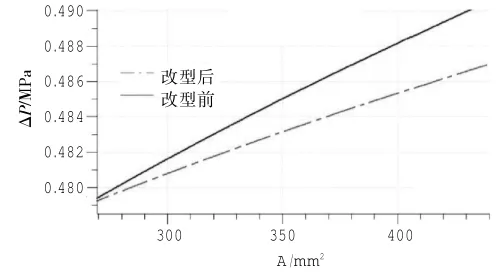
图9 改型前后压差随A变化情况

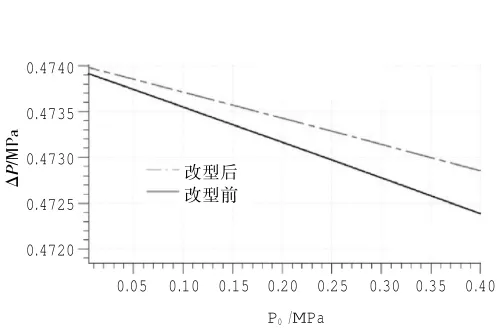
图10 改型前后压差随P0变化情况

6　动态性能的分析

以Ps输入为例，进行系统稳定性分析，验证Ps变化时改型前后系统的输出稳定性。计量面积A和回油压力P0为输入的分析与之同理，不作过多篇幅验证。

6.1辨识系统传递函数

改型后，在满足了降低压差偏移目标的同时，需要考虑改型是否影响系统的动态性能，即压差控制器从1个稳态到另1个稳态过渡的动态。这就要求调节时间不能过长，超调不能过大，要保证在稳定裕度不变小的前提下进行改型。

运用小偏差原理，通过系统辨识程序，分别辨识改型前后的传递函数。

在Ps阶跃输入信号下，压差活门位移与压差变化趋势一致，可用滑阀的位移变化来表征压差变化。同理在以面积A和回油压力P0的阶跃输入下，也可以用滑阀位移变化表征压差变化。

由于单位的关系，不同参数数值之间数量级相差较大，为避免出现较大的数值损失，且为使响应曲线更加明显利于辨识传函（实际超调小于25%），用归一化方法取系统的输入为ΔP/8 MPa输出为x'/0.3 mm。改型前和改型后系统阶跃响应曲线分别如图11和图12所示。

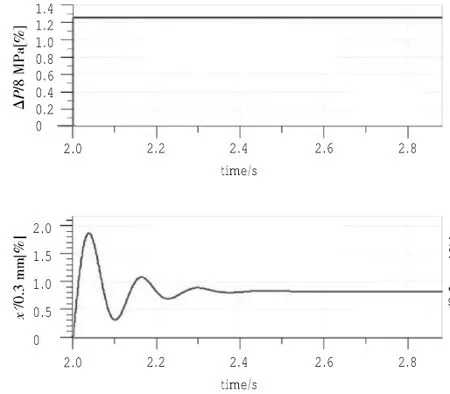
图11 改型前的输入与输出关系

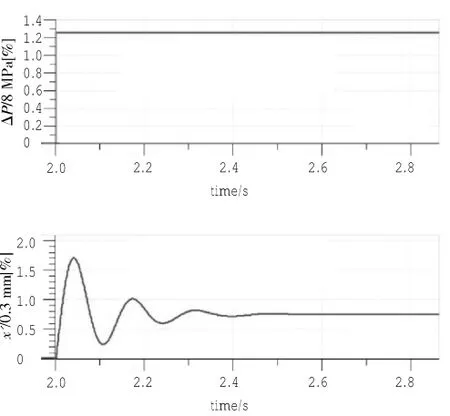
图12 改型后的输入和输出关系

辨识出的传递函数为

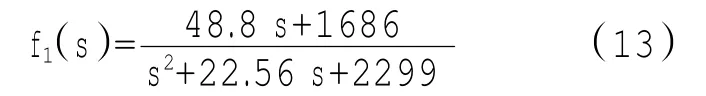
辨识所得的传递函数为

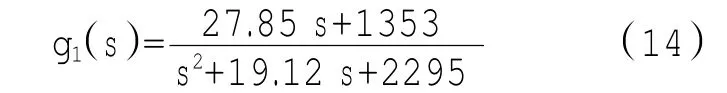
6.2分析改型前后稳定性

为得到改型前的稳定性，由传递函数式（13）可知，极点为-11.2781±49.7158i，均为负实部，且相角裕度为91.8814°，系统稳定。

为得到改型后稳定性，由式（14）可求得改型后系统极点为-9.5602±46.9401i。

其nyquist图[10]如图13所示。

从图中可见，曲线不与负实轴相交，其幅值裕度为无穷大，相角裕度稍有减小，为86.3519°，压差控制器仍然有很大的稳定裕度[11]。

对Ps加入脉动信号，正弦波模拟外部油压Ps脉动，验证其抗干扰性，输入和输出波形如图14所示，可证明其稳定性很好。

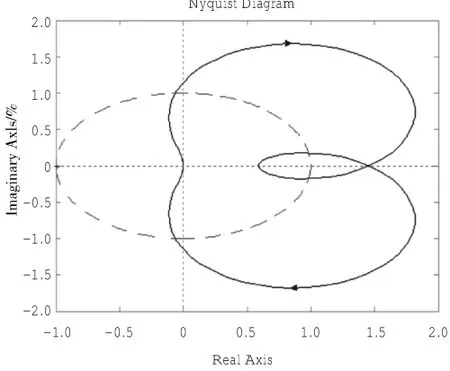
图13 改型后nyquist

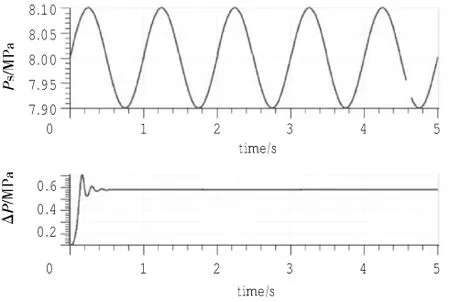
图14 输入Ps脉动的输入输出波形

7　结论

本文研究了某型压差控制器的性能影响因素，提出了改善压差偏移的措施，并改型原压差控制器，仿真表明达到了更好的控压差效果。通过以上分析得到了如下结论：

（1）为提高压差活门控压差性能，可以增大压差活门滑阀直径，增大阀口直径，降低弹簧刚度。鉴于增大滑阀直径对于控压差能力更明显，优先考虑增大滑阀直径。

（2）在动态分析中，压差控制器自身是1个稳定的系统，设计时要保证考虑其主要工作状态处于较大稳定裕度。

（3）分体式的压差控制器的部件较多，利用建立微分方程提取数学模型较为复杂，采取的辨识传递函数为近似拟合方法，精度有限。对于精度要求更高的起动总管等为一体式压差控制器，建议采用微分方程提取数学模型得到传递函数。

（4）对于3个参数，应该存在1组最佳组合，既能提高控压差能力，又能使动态损失最小，需要精确建立压差控制器的数学模型。但分体式的传递函数提取较为复杂，最优参数的定量求解方法可以在后续工作中以一体式压差控制器为对象进行研究。

参考文献：

[1]尚洋，郭迎清，王磊.压差控制器设计参数对燃油计量系统影响研究[J].航空制造技术，2013（6）：89-91. SHANG Yang，GUO Yingqing，W ANG Lei.Study of impact of design parameter of differential pressure controller on fuel metering system[J]. Aeronautical Manufacturing Technology，2013（6）：89-91（.in Chinese）

[2]康伟，潘宏亮，周鹏.某型发动机燃油控制执行机构仿真与验证试验[J].系统仿真学报，2010，22（1）：120-124. KANG W ei，PAN Hongliang，ZHOU Peng.Simulation and validation of turbojet fuel control actuator[J].Journal of System Simulation，2010，22 （1）：120-124（.in Chinese）

[3]杨峰，刘雄，贾盼盼，等.某型压差活门的动态分析与研究[J].动力控制，2014，20（1）：48-52. YANG Feng，LIU Xiong，JIA Panpan，et al.The dynamic analysis and study of hydraulic pressure compensator [J].Engine Control，2014，20 （1）：48-52（.in Chinese）

[4]曾德堂，王曦，覃道亮，等.燃油计量装置回油型面特性分析[J].航空发动机，2010，36（6）：23-25. ZENG Detang，WANG Xi，TAN Daoliang，et al. Fuel scavenger con-tour performance analysis of fuel metering devices [J]. Aeroengine，2010，36（6）：23-25.(in Chinese)

[5]樊思齐，李华聪，樊丁.航空发动机控制[M].西安：西北工业大学出版社，2008：178-180. FAN Siqi，LI Huacong，FAN Ding.Aeroengine control[M].Xian：North-western Polytechnical University Press，2008：178-180.（in Chinese）

[6]颜庆津.数值分析[M].北京：北京航空航天大学出版社，2006：207-215. YAN Qingjin. Numerical analysis [M]. Beijing：Beihang University Press，2006：207-215.(in Chinese)

[7]林建亚，何存兴.液压元件[M].北京：机械工业出版社，1988：10-14. LIN Jianya，HE Cunxing. Hydraulic components [M]. Beijing：China MachinePress，1988：10-14.（in Chinese）

[8]盛敬超.工程流体力学[M].北京:机械工业出版社，1988：54-56. SHENG Jingchao.Engineering fluid mechanics[M].Beijing：China Ma-chine Press，1988：54-56.（in Chinese）

[9]李华聪，李吉.机械/液压系统建模仿真软件AMESim[J].计算机仿真，2006，23（12）：294-297. LI Huacong，LI Ji.Modeling and simulation software AMESim for me-chanical/hydraulic system [J]. Computer Simulation，2006，23（12）：294-297.（in Chinese）

[10]薛定宇.控制系统计算机辅助设计[M].北京：清华大学出版社，2006:157. XUE Dingyu.Computer aided control system design [M].Beijing：Ts-inghua University Press，2006：157.（in Chinese）

[11]胡寿松.自动控制原理[M].北京：国防工业出版社，1984：95. HU Shousong.Principle of automatic control[M].Beijing：National De-fense Industry Press，1984：95.（in Chinese)

[12]刘铁庚.新型中小发数控系统燃油计量装置设计方案[J].测控技术，2012，31(增刊)：344-346. LIU Tiegeng.An innovational design of a fuel metering unit for small aero engine [J].Measurement and Control Technology，2012，31（S）：344-346.（in Chinese）

[13]W ang Huawei，W ang Xi，Dang W ei，et al.Generic design methodology for electro-hydraulic servo actuator in aero-engine main fuel control system [R].ASME 2014-GT-27337.

[14]周立峰.发动机燃油计量装置特性仿真与试验研究[D].南京：南京航空航天大学，2010. ZHOU Lifeng.Simulation and experiment study for characteristics of engine fuel measurement equipment[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2010.（in Chinese）

[15]付永领，祁小野.LMS Imagine.Lab AMESim系统建模与仿真参考手册[M].北京：北京航空航天大学出版社，2011：32-76. FU Yongling，QI Xiaoye.LMS Imagine.Lab AMESim modeling and simulation of system reference manual[M].Beijing：Beihang University Press，2011：32-76.

（编辑：赵明菁）

Differential Pressure Controller Stability Analysis and Research of Design Parameters

LI Hong-sheng1,2,3,WANG Xi2,3,WANG Hua-wei2,3,DANG Wei2,3,ZHANG Geng2,3
（1.AVIC China Gas Turbine Establishment,Chengdu 610500,China;2.Collaborative Innovation CenterofAdvanced Aero-Engine, Beijing 100191,China;3.School of Energy and Power Engineering,Beihang University,Beijing 100191,China）

Abstract:As an important part of aeroengine fuel measurement,differential pressure controller is used to keep the pressure drop constant of the measurement valve.In order to explore the factors of its ability,the differential pressure controller in an aeroengine afterburner was studied.The main factors that impact on the ability of control pressure drop were analyzed and deduced.Then a model was established with AMESim.Simulation was carried out to prove the correctness of the conclusion.Based on the fixed component,the differential pressure controller was remodeled reasonably.In order to keep the stability of the system from the improvement,a technical modification was done to get the transform function by using small deviation linearization method.Theoretical foundation which can improve the ability of differential pressure controller was got eventually.

Key words:differential pressure controller;hydraulic control;stability;AMESim model simulation;stability margin;metering valve

中图分类号：V233.2+2

文献标识码：A

doi：10.13477/j.cnki.aeroengine.2016.03.003

收稿日期：2015-06-12

作者简介：李洪胜（1989），男，硕士，助理工程师，主要从事航空发动机控制系统研究工作；Email：lhs_buaa@163.com。