2级涡轮内部流动定常与非定常计算差异研究

杨　杰，周　颖，潘尚能，卢聪明（中航工业航空动力机械研究所，湖南株洲412002）



2级涡轮内部流动定常与非定常计算差异研究

杨杰，周颖，潘尚能，卢聪明
（中航工业航空动力机械研究所，湖南株洲412002）

摘要：为获取进而认识涡轮内部流动状态，以某2级约化形式的动力涡轮为研究对象，分别对其进行定常和非定常数值计算和分析。研究表明：定常计算与非定常计算对涡轮内部流动的模拟结果，如叶片表面的压力分布、叶排进出口的气流角、叶片通道中的二次流流向涡、展向涡、叶片通道中的损失等，均存在差异；流动的非定常性越强，定常与非定常计算结果的差异越大，且该差异大小对于静叶与动叶呈相反的展向分布规律。

关键词：涡轮；内部流动；定常；非定常；数值模拟；涡；航空发动机

引用格式：杨杰，周颖，潘尚能，等.2级涡轮内部流动定常与非定常计算差异研究[J].航空发动机，2016,42（3）：21-27.YANG Jie,ZHOU Ying,PAN Shangneng,et al.Study of differences between steady and unsteady computation for two-stage turbines internal flow[J].Aeroengine,2016,42(3):21-27.

0　引言

对涡轮内部流动的数值模拟是获取进而认识涡轮内部流动状态的重要手段，有定常计算和非定常计算2种方法。定常计算方法所需的计算机硬件资源少、花费的机时少，能快速获取模拟结果。涡轮内部的流动本质上是非定常的，定常的数值计算必然会丢失相关的非定常信息，无法获取非定常流动特征。掌握定常计算结果与非定常计算结果之间的差异是衡量选用何种计算方式的重要依据，更是工程计算中用定常计算代替非定常计算的必要前提。对于叶轮机械的内部流动的定常和非定常数值模拟，国外[1-5]和国内[6-10]的学者都进行了大量研究，然而对于定常计算与非定常计算之间的差异的系统研究在公开文献中还很少见。

本文以某2级动力涡轮为研究对象开展了定常计算与非定常计算的对比研究。

1　研究方法

1.1研究对象

选取某2级动力涡轮为研究对象。该涡轮4排叶片数之比为0.98∶1∶1.04∶1，不成简单整数比。为了减小非定常模拟的计算量，对该涡轮的2排导叶进行了叶片数约化处理，将2排导叶的叶片数调整成与2排动叶的叶片数相等。约化后，4排叶片数之比为1∶1∶1∶1，即4排叶片的数目相等。这样在非定常计算时，可充分利用周期性边界条件，每排叶片通道均只取1个。

该涡轮2排动叶均带冠和篦齿封严，但为了模拟叶尖泄漏流，取消了2排动叶的叶冠和篦齿，2排动叶的叶尖间隙均取0.15 mm。

1.2数值模型

流场的定常和非定常模拟采用商用软件CFX求解定常的和非定常的雷诺平均方程来实现。其中湍流的模拟采用带有自动壁面处理功能的剪切应力输运模型（SST模型）；时间项的离散采用2阶向后欧拉格式，对流项和湍流项的离散均采用高阶格式。进行非定常计算时，时间步长取1倍第1级动叶通过周期（即转子转过1个第1级动叶通道的时间，实际上，由于各排叶片数相等，故各叶排的叶片通过周期相同）的1/30。非定常计算进行约70个动叶通过周期后，得到了流场的收敛解。

1.3计算模型

计算网格采用商用软件TurboGrid生成。定常和非定常计算采用相同的网格和计算域。整个计算域包括4排单叶片通道，总网格量约为160万。各叶片通道叶片表面Y+值不超过30。2排动叶叶尖间隙内有15层网格。计算域进口位置距离第1级静叶前缘约1.5倍、叶中处轴向弦长；计算域出口位置距离第2级动叶尾缘约为5倍叶中处轴向弦长。封严和泄漏位置处的网格通过商用软件ICEM标出。计算网格如图1所示。

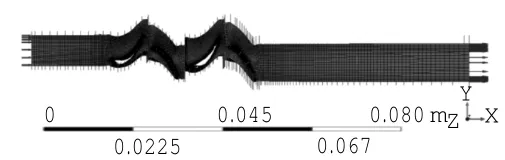
图1 计算网格

计算域进口给定总温、总压、进气方向、来流湍流度，出口给定平均静压。计算域展向两侧及叶片表面给定无滑移壁面边界条件，周向两侧设置为周期性边界。静子区域与转子区域的交接面在非定常计算时采用滑移面处理方式；在定常计算时采用混合面处理方式；在为获取非定常计算所需的初场定常计算中采用固结转子处理方式。

2　研究结果

2.1计算成本分析

约化后涡轮的定常和非定常计算的成本对比见表1（二者具有相同的计算网格和计算域）。从表中可知，非定常计算在CPU和内存消耗均比定常计算大的情况下，时间花费是定常计算的91倍。从CPU、内存、时间花费的综合成本来看（综合成本定义为CPU、内存、时间3项成本之积），非定常计算的综合成本是定常计算的176倍。由此可见，从计算经济性来看，定常计算相对于非定常计算而言，有着巨大的优势。

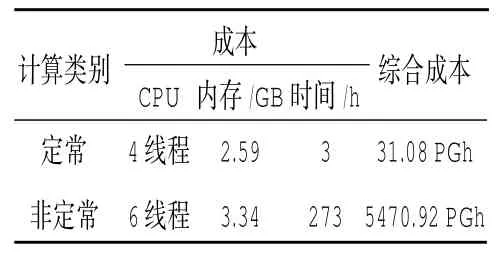
表1 定常和非定常计算成本对比

2.2性能参数分析

关于性能参数，约化后涡轮定常和非定常计算结果的对比见表2。其中流量和功率以原涡轮定常计算的结果为基准进行了无量纲化，称为相对流量和相对功率。其中效率为总对总等熵效率，即实际总焓降与总对总等熵焓降之比。

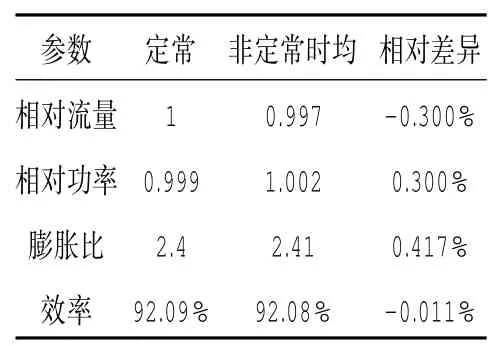
表2 性能参数的计算结果

从表中可见，对于涡轮的流量、功率、膨胀比、效率等性能参数而言，涡轮的定常计算结果与非定常计算的时均结果相差很小。流量、功率和膨胀比的变化不超过0.5%，效率的变化不超过0.1%。这表明对于该涡轮而言，其定常性能与非定常时均性能差别很小。

涡轮各排叶片通道区域的总压恢复系数的定常计算结果与非定常计算的时均结果的对比如图2所示。某排叶片通道的总压恢复系数定义为该排叶片通道出口总压与进口总压之比（静叶排为绝对总压之比，动叶排为相对总压之比）。从图中可见，S1区域的总压恢复系数的定常计算结果与非定常计算的时均结果几乎无差别；对于R1区域与S2区域，总压恢复系数的非定常时均结果比定常结果略低，相差不超过0.1%；对于R2区域，总压恢复系数的非定常时均结果比定常结果低约0.3%。这说明除S1区域外，其他各叶排区域的损失的非定常时均结果比定常结果要大，但相差不大。

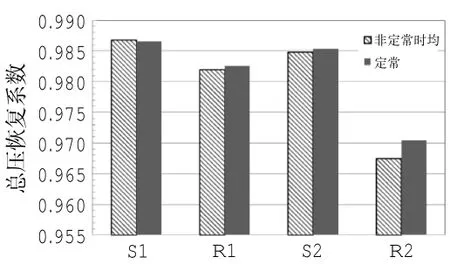
图2 各排叶片通道区域总压恢复系数定常与非定常时均结果对比

约化后涡轮非定常计算得到的效率与各排叶片通道区域的总压恢复系数随时间的变化情况如图3所示。从图中可见，约化后涡轮的效率与各排叶片通道区域的总压恢复系数的变化周期均为1个静叶或动叶通过周期（各叶排的叶片通过周期相同）。效率的变化幅值为0.61%，这说明效率在1个叶片通道周期内的变化不超过0.7个百分点，即其非定常效应较弱。各排叶片通道区域的总压恢复系数随时间变化的相位存在差异，例如S2区域与R1区域几乎反相。事实上，涡轮效率的非定常效应较弱正是与各排叶片通道区域的损失存在相位差异有关，当某叶排通道区域的损失较大时，另外的叶排通道区域的损失较小，反之亦然，从而使总损失和效率的变化较弱。另外，由于各叶排通道区域的时均损失与定常计算的结果相差也不大，故涡轮非定常时均效率与定常计算的结果相差很小。

图3 效率与总压恢复系数随时间变化

2.3流动分析

本节对约化后涡轮的定常计算和非定常计算得到的流动细节进行分析。

2.3.1第1级静叶

第1级静叶在5%、50%和95% 3个展向位置处的表面的定常压力、非定常时均压力、非定常最大值与最小值压力的分布的对比如图4所示。非定常最大值与最小值压力即流场中某点压力随时间变化周期中的最大值与最小值。

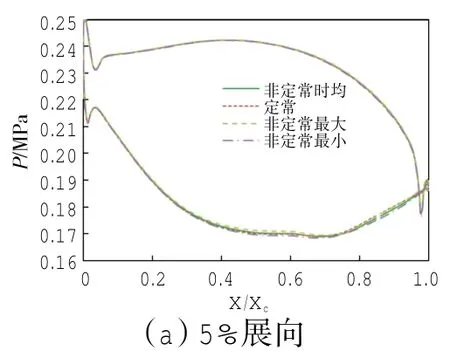
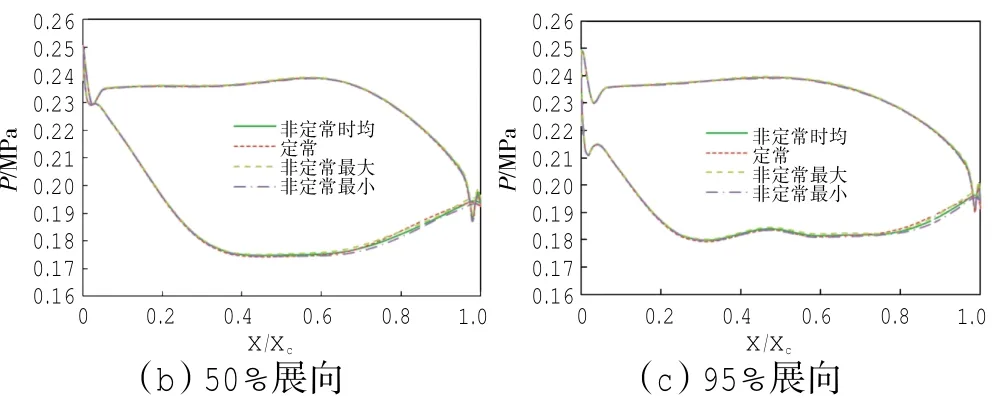
图4 第1级静叶表面压力分布

从图中可见，在叶根、叶中、叶尖3个展向位置处，第1级静叶表面的定常与非定常时均压力分布都只是在吸力面后段上微有差异，而且非定常最大值与最小值压力的分布也只是在吸力面后段上有较小差异。这表明在第1级静叶通道中，流动的非定常性很弱，定常与非定常计算的差异很小。事实上，第1级静叶通道中流动的非定常性只有来自下游第1级动叶的势扰动这一较弱的源头，故其非定常性很弱，且只表现在通道后段。

2.3.2第1级动叶

第1级动叶在5%、50%和95% 3个展向位置处的表面的定常压力、非定常时均压力、非定常最大值与最小值压力的分布的对比如图5所示。

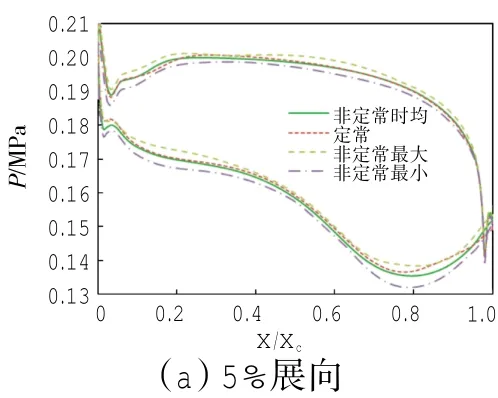
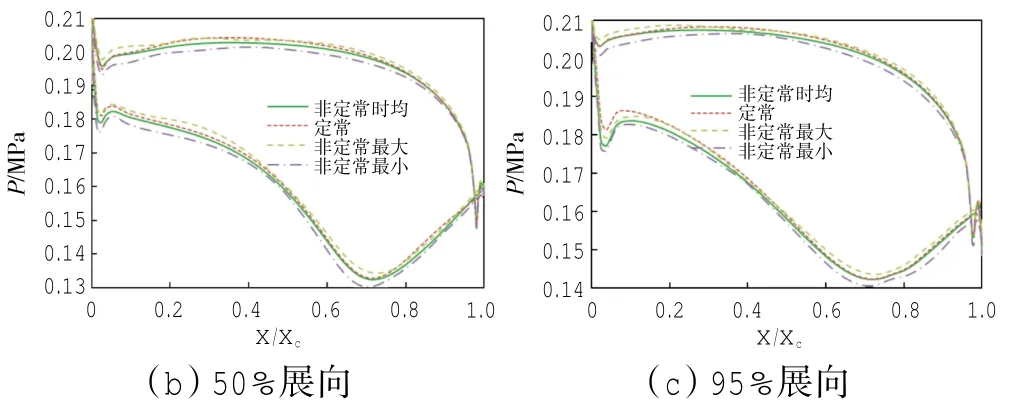
图5 第1级动叶表面压力分布

从图中可见，在叶根、叶中和叶尖3个展向位置处，第1级动叶表面的最大值压力与最小值压力的分布有显著差异，而且定常压力分布与非定常时均压力分布也有明显区别。这表明在第1级动叶通道中，流动的非定常性已经很显著，定常计算的结果与非定常计算的时均结果已经有明显区别。

定常与非定常时均压力分布值差异大的位置一般就是非定常压力最大值与最小值相差大的位置，即非定常压力扰动强的位置，这说明定常计算结果与非定常计算时均结果的差异是由于流动的非定常性造成的。

第1级转子进口的涡量云图（包括流向涡和展向涡）的定常计算结果与非定常计算的时均值、标准差的对比如图6所示。从图6（a）、（c）中对比可见，第1级转子进口定常计算的流向涡在通道上方和下方均与非定常计算的时均结果有明显差异，在通道中间区域的差别较小。事实上，由于二次流流向涡自身就具有典型的非定常流动特征，遵循自身的时间演化规律，而且受到转静干涉的影响，非定常特性非常明显。从图6（e）中可见，通道上方和下方的流向涡的强度随时间变化很剧烈，表现出很强的非定常性，这也正与图6（a）、（c）有差异的地方对应，说明非定常计算能有效地模拟出二次流流向涡的非定常特性。而定常计算一方面对通过转静交接面的通量进行了平均，导致对二次流流向涡模拟得不准；另一方面无法模拟由于转子转动产生的非定常特性，从而无法模拟二次流流向涡的时间演化规律及其非定常特性。事实上，图6（a），（c）显示定常计算模拟的通道上方和下方的二次流流向涡比非定常时均结果明显偏弱。

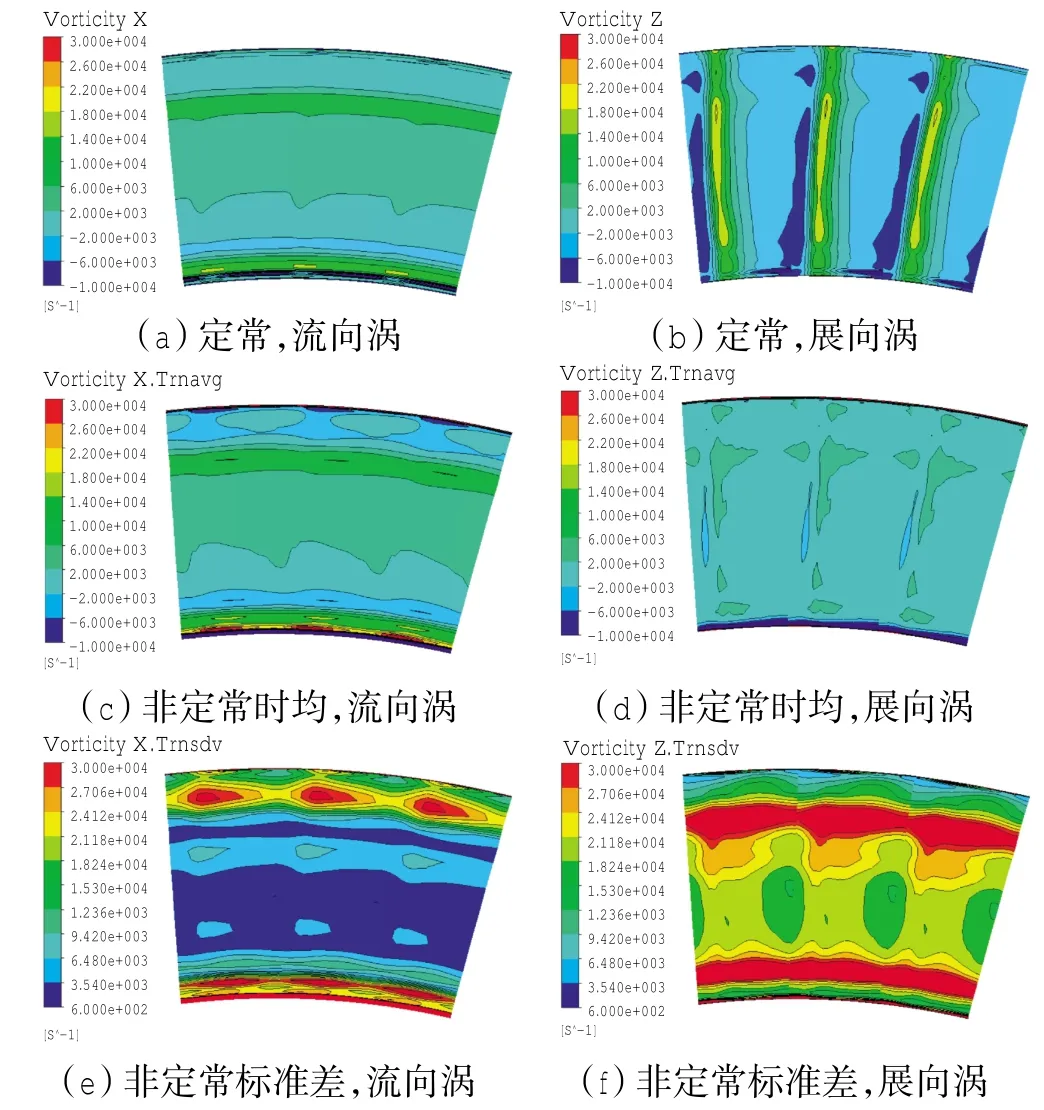
图6 第1级转子进口涡量

定常计算对第1级动叶进口展向涡的模拟结果如图6（b）所示。图中的高涡量区是第1级静叶尾迹所在位置。由于在定常计算中，转子的转动没有被模拟，故转、静子的相对周向位置不变，故第1静叶的尾迹相对于第1级动叶的位置也不变。说明在定常计算中，当计算设置的转、静子相对周向位置不同时，对于尾迹模拟的结果不同，对于上游展向涡与下游叶片的相互作用也不同，而实际上在进行定常计算时，基本上都忽略了对转、静子叶片排相对周向位置的考虑。对第1级动叶进口展向涡进行非定常模拟的时均结果如图6（d）所示。图中并不像图6（b）中显示出展向涡明显的周向分布，即尾迹位置。事实上，在非定常计算中，由于转子的转动被模拟，故在1个静叶通过周期内，静叶尾迹均匀地经过动叶通道的各周向位置，故展向涡的非定常时均结果中其周向分布基本上被抹平；另外，由于在非定常计算中，转子的转动被模拟，故计算设置中的转、静子叶片排相对位置无需考虑。非定常计算模拟的展向涡的标准差如图6（f）所示。从图中可见，上下2个高值区域正与图6（b）中的展向涡中的上下2个高涡量区域对应，即在上游尾迹的上下2个涡核中，动叶通道中展向涡的非定常性是最强的。图6（f）中显示第1级动叶进口的展向涡非定常标准差在周向上的差异并未完全抹平，事实上图6 （d）中的展向涡的非定常时均结果在周向上也仍有些差异，这是由于转子转动产生的非定常干涉造成的。转、静子相对周向位置不同，转、静干涉作用会有差异，从而造成图6（d）、（f）中展向涡时均值和标准差在周向上的差异。

图9 第1级动叶通道总压恢复系数展向分布

第1级动叶出口流向涡与展向涡标准差的云图如图7所示，第1级动叶出口气流角展向分布的定常计算结果与非定常计算时均结果的对比如图8所示，第1级动叶通道区域总压恢复系数展向分布的定常计算与非定常计算时均结果的对比如图9所示。

从图8与图7的对比中可见，第1级动叶出口气流角定常计算结果与非定常计算时均结果差异较大的展向位置，正与图7中的高值区域对应，表明二次流流向涡和展向涡的非定常性是第1级动叶出口气流角的定常计算结果与非定常计算时均结果存在差异的原因；且非定常性越强，差异越大。

同样，从图9与图7的对比中可见，定常与非定常计算得到的第1级动叶通道区域损失的差异也是源于二次流流向涡和展向涡的非定常性；且非定常性越强，差异越大。

2.3.3第2级静叶

第2级静叶在5%、50%和95% 3个展向位置处表面的定常压力、非定常时均压力、非定常最大值与最小值压力的分布如图10所示。对比图10与图5可见，在各展向位置处，第2级静叶表面压力的非定常最大、最小值分布的差异比第1级动叶要显著得多，即第2级静叶通道中的流动非定常性要比第1级动叶通道要强得多，而且越靠近叶尖，非定常性越强。相应地在各展向位置，第2级静叶表面的定常与非定常时均压力的差异也比第1级动叶的要显著得多，且总体而言，越靠近叶尖，差异越显著。

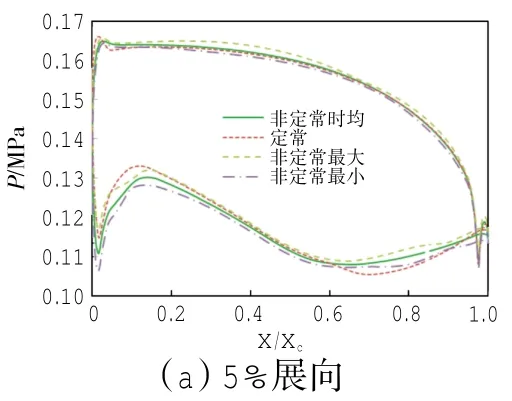
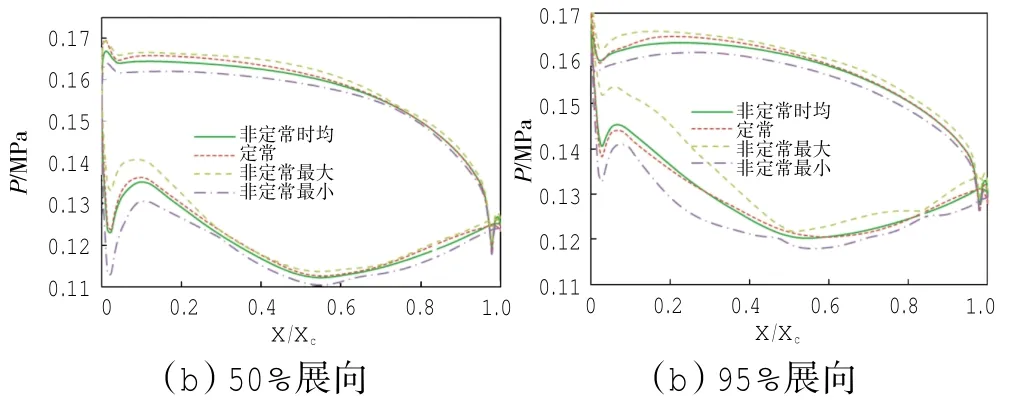
图10 第2级静叶表面压力分布

第2级静叶通道中流动的非定常扰动的源头包括来自上游动叶的势干涉、尾迹干涉、叶尖泄漏流的干涉和来自下游动叶的势干涉，而且其上游流动本身就具有非定常性，故上游流动的非定常性经过第2级静叶通道中的这些非定常扰动源的干涉而得到加强，因而第2级静叶通道中流动的非定常性要比第1级动叶通道的要强。越靠近叶尖，第2级静叶的叶片弦长越大，叶片稠度倾向于增大，而且受上游动叶叶尖泄漏流的影响越强，故上述非定常扰动源与叶片的干涉越强。

2.2.4第2级动叶

第2级动叶在5%，50%，95%这3个展向位置处的压力分布的定常计算结果和非定常计算的时均值、最大值、最小值结果的对比如图11所示。从图中可见，在各展向位置处第2级动叶表面的压力分布的定常计算的结果与非定常计算的时均结果都有极为显著的差异，比第2级静叶表面压力分布（图10）的差异更为显著。在各展向位置处，均是吸力面处的差异要大于压力面处的差异；叶片前段的差异大于叶片后段的差异；5%展向位置处的差异最大，在该处的吸力面上存在巨大的差异。

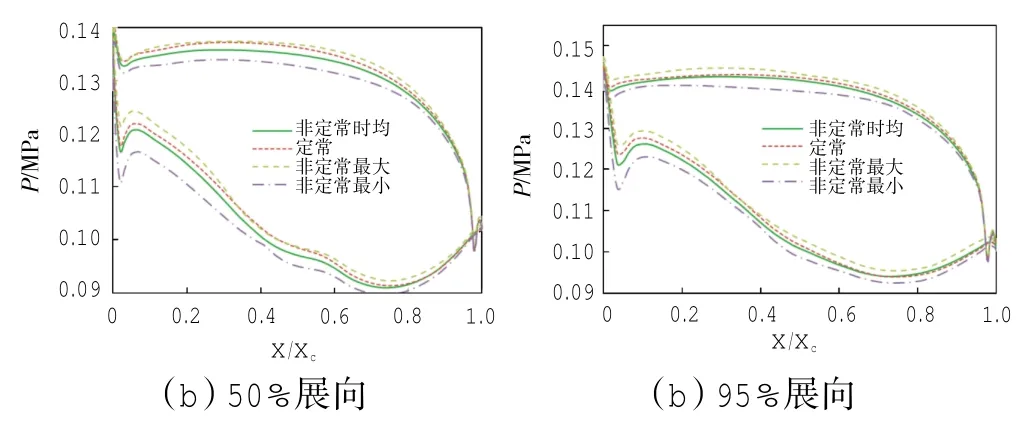
图11 第2级动叶表面压力分布

与图5和图10一样，图11中的定常结果与非定常时均结果差异大的位置一般正是非定常最大值与最小值的差异大的位置，即流动的非定常性强的位置；表明第2级动叶表面压力分布的定常计算结果与非定常计算的时均结果的差异与前3排叶片一样，也是由通道中流动的非定常性造成的。第2级通道中流动的非定常性源头主要是来自上游静叶的尾迹干涉和势干涉，已不存在来自下游的非定常扰动源，故在各展向位置处，第2级动叶后段处的压力扰动小，压力分布的定常计算结果与非定常计算的时均结果差异小。由于第2级动叶的稠度随展向高度的减小而增大，故非定常扰动源与动叶的干涉沿展向高度的减小而增强，故展向位置越低，第2级动叶上的压力扰动越大，压力分布的定常计算结果与非定常计算的时均结果差异越大。来自上游第2级静叶通道中的流动的非定常性，在第2级动叶通道的前段中由于上游非定常扰动源的作用而加强；而在第2级动叶通道的后段中由于没有来自下游的非定常扰动源，流动的非定常性减弱。

第2级动叶后10%倍叶中轴向弦长处的涡量云图的定常计算结果与非定常计算的时均值、标准差的对比如图12所示。从图中可见，在第2级动叶后不远处的截面位置，二次流流向涡和展向涡的定常计算结果与非定常计算的时均结果在拓扑上是基本一致的，有差异的区域正与图12（e）、（f）中的标准差的高值区域相对应，即定常计算与非定常计算结果的差异是由于二次流流向涡和展向涡的非定常性造成的。

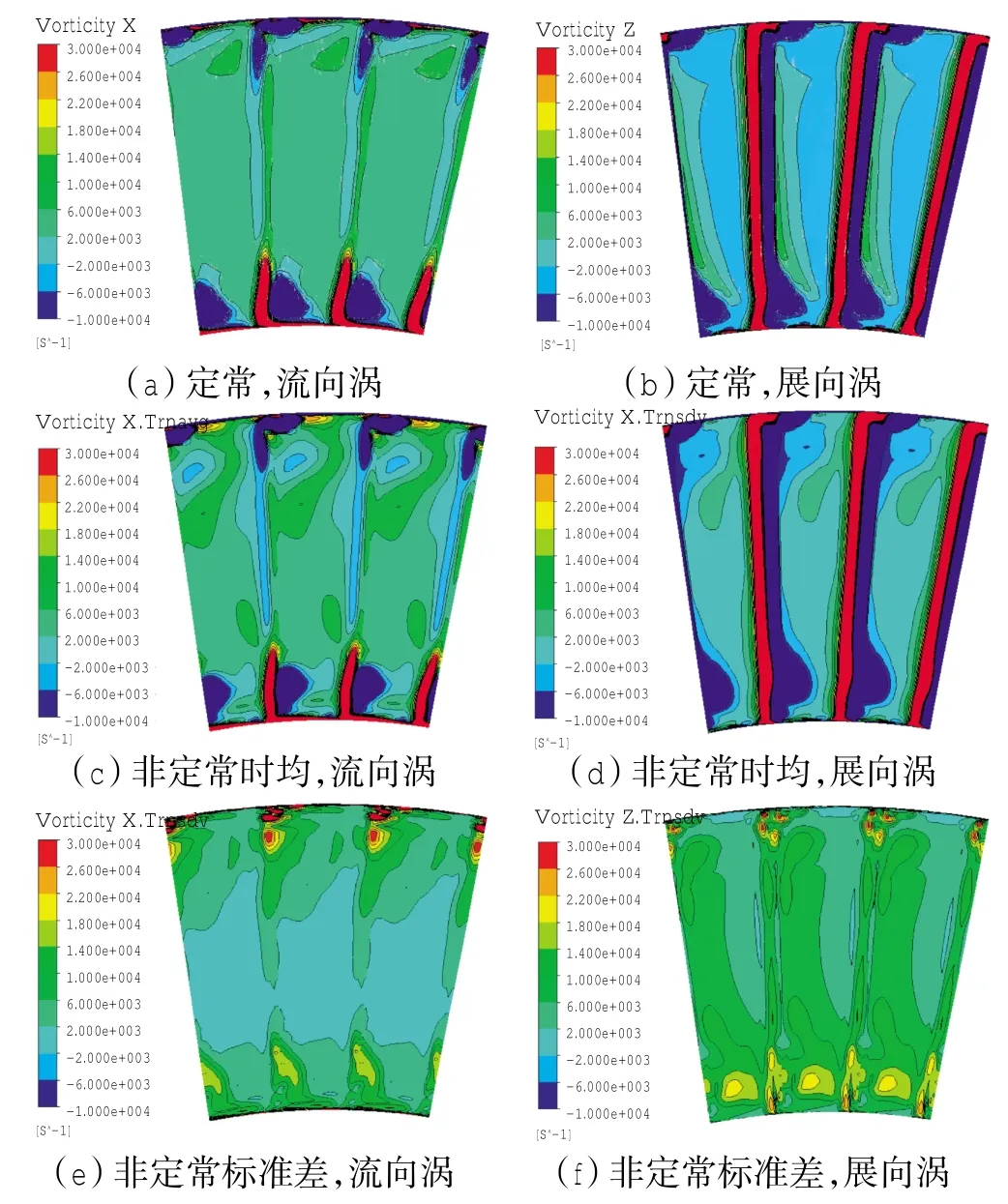
图12 第2级动叶后10%倍叶中轴向弦长处涡量

图13 第2级动叶通道出口涡量

第2级动叶通道出口处的涡量云图的定常计算结果与非定常计算的时均值、标准差的对比如图13所示。从图中可见，在第2级动叶通道出口处，二次流流向涡和展向涡的定常计算结果与非定常计算的时均结果都趋于一致，而且在周向上趋于均匀。从图13 （e）、（f）中可见，第2级动叶通道出口处的二次流流向和展向涡的非定常性已趋于消失。事实上，由于从第2级动叶出口到通道出口有近5倍第2级动叶叶中轴向弦长的一段通道。在如此长的通道中均不存在来自下游的非定常扰动，故来自第2级动叶出口的气流的非定常性和周向非均匀性，通过在如此长的通道中的流动耗散和掺混，会大幅度地减弱，以至于在通道出口处，气流的非定常性和周向非均匀性趋于消失。

3　结论

通过对某2级动力涡轮内部流动的定常和非定常计算结果的对比研究，可以得到如下结论：

（1）由于涡轮内部流动固有的非定常性的存在，定常与非定常计算对涡轮内部流动的模拟结果，如叶片表面的压力分布，叶排进出口的气流角、叶片通道中的二次流流向涡与展向涡、叶片通道中的损失等，均存在差异。流动的非定常性越强，定常与非定常的计算结果差异越大。

（2）2级涡轮的第1排叶片通道中的流动的非定常性最弱，其定常与非定常计算结果的差异最小；随着气流向后排叶片通道中输运，流动的非定常性增强，从而定常与非定常计算结果的差异增大；在最后1排叶片通道中，流动的非定常性最强，定常与非定常计算结果的差异也最大；在最后1排叶片后的无叶片长通道中，流动的非定常性发生衰减，到达通道出口时，流动的非定常性趋于消失，定常与非定常计算结果的差异也趋于消失。

（3）在2级涡轮的叶片排中，定常与非定常结果的差异，总体来说，对于静叶而言，倾向于高展向位置处比低展向位置处大；对动叶而言，倾向于低展向位置处比高展向位置处大。越是后面叶片排，流动非定常性越强，这种趋势越明显。

（4）各非定常扰动源的相互作用，使得涡轮总性能的非定常性较弱，总性能的定常与非定常计算的结果相差不大。

（5）定常与非定常计算结果的差异大小取决于流动非定常性的强弱。在工程计算中，决定采用定常计算代替非定常计算前，需要评估流动的非定常性。

参考文献：

[1]Giles M B.Calculation of unsteady wake/rotor interactions [R].AIAA-87-0006.

[2]Gondy-Burlet K L，Rai M M，Madavan N K.Unsteady three dimen-sional Navier Stokes simulations of multistage turbomachinery flows[R]. AIAA-93-1979.

[3]Dawes W N.Simulating unsteady turbomachinery flows on unstructured bashs which adapt both in time and space[R].ASME 93-GT-104.

[4]Davis R L，Shang T，Buteau J，etal.Prediction of 3D unsteady flow in multistage turbomachinery using an implicit dual timestep approach[R]. AIAA-96-2565.

[5]Suzen Y B，Huang P G.Numerical simulation of unsteady wake/blade interactions in low-pressure turbine flows using an intermittency trans-port equation[J].Journal of Turbomachinery，2005，127（3）：431-444.

[6]季路成，周盛.一个跨音风扇级转/静干扰流动的时间精确模拟[J].工程热物理学报，1999，20（4）：426-430. JI Lucheng，ZHOU Sheng.Time-accurate simulation of a transonic fan stage on rotor/stator interaction [J].Journal of Engineering Thermo-physics,1999，20（4）：426-430（.in Chinese）

[7]刘前智，周新海.单级跨音压气机三维非定常粘性流动计算[J].航空动力学报，2000，15（1）：12-16. LIU Qianzhi，ZHOU Xinhai.Computation of 3D unsteady viscous flow in transonic compressor stage[J].Journal of Aerospace Power，2000，15 （1）：12-16（.in Chinese）

[8]刘前智，周新海.多级压气机非定常流动的数值模拟[J].推进技术，2001，22（5）：408-410. LIU Qianzhi，ZHOU Xinhai.Numerical analysis of unsteady flow in multistage compressors [J].Journal of Propulsion Technology，2001，22 （5）：408-410.（in Chinese）

[9]董素艳，刘松龄，朱惠人.二维涡轮级的定常/非定常数值模拟[J].推进技术，2001，22（5）：387-391. DONG Suyan，LIU Songling，ZHU Huiren.Two dimensional steady/un-steady numerical simulation in a turbine stage[J].Journal of Propulsion Technology，2001，22（5）：387-391.（in Chinese）

[10]刘前智.双级风扇三维粘性非定常流动的数值解[J].航空动力学报，2003，18（6）：768-771. LIU Qianzhi.Numerical solutions of 3D unsteady viscous flow in a two-stage fan[J].Journal of Aerospace Power，2003，18（6）：768-771. （in Chinese）

[11]解亚东，朱贤，丁建国.大涵道比风扇转子的非定常数值模拟[J].航空发动机，2015，41（4）：20-23. XIE Yadong，ZHU Xian，DING Jianguo.Unsteady numerical simula-tion of high bypass ratio fan[J].Aeroengine，2015，41（4）：20-23.（in Chinese）

[12]邵飞，綦蕾，罗建桥，等.高压涡轮全环非定常流动数值模拟[J].航空发动机，2014，40（2）：31-37. SHAO Fei，QILei，LUO Jianqiao，et al.Numerical simulation of full scale unsteady flow in high pressure turbine [J].Aeroengine，2014，40 （2）：31-37.（in Chinese）

（编辑：张宝玲）

Study of Differences between Steady and Unsteady Computation for Two-Stage Turbine Internal Flow

YANG Jie,ZHOU Ying,PAN Shang-neng,LU Cong-ming
（AVIC Aviation Power-Plant Research Institute,Zhuzhou Hunan 412002,China）

Abstract:In order to find out internal flow state of turbine,taking a scaled two-stage power turbine as the research object,both steady and unsteady computations were conducted.The study shows that there makes obvious difference in the results of both steady and unsteady computation on the internal flow of turbines,including the pressure distribution on blade surfaces,the inlet/outlet flow angles of blade rows, the secondary flow streamwise and spanwise vortex in blade passages,the flow loss in blade passages.Moreover,the stronger the unsteadies of the flow show,the larger differences between steady and unsteady computation results are,and the magnitude of the differences between steady and unsteady computation results tend to follow opposite spanwise distribution rules for stators and rotors.

Key words:turbine；internal flow；steady；unsteady；simulation；vortex；aeroengine

中图分类号：V231.3

文献标识码：A

doi：10.13477/j.cnki.aeroengine.2016.03.005

收稿日期：2015-11-06

作者简介：杨杰（1983），男，博士，工程师，主要从事航空发动机涡轮气动设计与研究工作；E-mail:yjguy@126.com。