高转速大长径比传动杆动态特性研究

郭　霞，章焕章，程小勇，王少波（中航商用航空发动机有限责任公司，上海201108）



高转速大长径比传动杆动态特性研究

郭霞，章焕章，程小勇，王少波
（中航商用航空发动机有限责任公司，上海201108）

摘要：大客发动机径向传动杆具有长径比大、转速高等特点。为保证传动杆可靠工作，需进行精确的动态特性分析，而边界条件的选取和简化是保证传动杆动态特性准确性的关键。分别使用了简化模型和整体模型计算了传动杆的模态，通过边界条件的选取设置，对传动杆进行了动态特性分析和试验验证，并与试验结果进行了对比。结果显示，使用整体模型计算得到的传动杆模态振型与试验结果较为一致，证明了传动杆边界条件选取方法的正确性。

关键词：传动杆；动态特性；模态；有限元；试验验证

引用格式：郭霞，章焕章，程小勇，等.高转速大长径比传动杆动态特性研究[J].航空发动机，2016,42（3）：28-32.GUO Xia,ZHANG Huanzhang,CHENG Xiaoyong,et al.Dynamic characteristics study on transmission rod with high speed and large aspect ratio[J].Aeroengine,2016,42(3):28-32.

0　引言

大型客机发动机径向传动杆具有转速高（大于20000 r/min）、长径比大（大于30）的特点。其主要作用是从中央传动杆提取功率，带动发动机各附件工作。为了调整传动杆的临界转速，通常需要在传动杆的中间位置设置辅助支承轴承，传动杆两端分别通过花键与齿轮相连。由于传动杆属于多自由度的运动机构，各结构间会相互作用和影响，给传动杆转子系统的动力特性带来极大的不确定性。同时，传动杆结构复杂，工作环境恶劣，在设计阶段需要对其进行振动特性计算，以保证其可靠工作[1-3]。

传动杆属于系统工作部件，其工作特性会受到所在系统的影响。可以对传动杆单独施加边界条件进行模态计算，即简化模型；也可以对传动杆所在的系统施加边界条件进行计算，即系统模型。传动杆模态的计算结果完全取决于边界条件的设置，对于简化模型，需合理模拟传动杆的支承结构，计算相应的支承刚度；对于系统模型，则需建立传动杆及其支承结构的模型。找到1套能准确计算传动杆模态的方法，以指导传动杆的准确设计，是保证其可靠工作的前提。

本文针对大型客机发动机径向传动杆的特点，通过数学模型分析，分别建立了简化模型和系统模型，通过有限元方法计算了传动杆的模态，并将2种计算结果与传动杆模态试验结果进行对比。

1　计算方法

传动系统由多个自由度构成，任何运动都可以用其振动模态合成，通过不同模态的线性组合体现整个系统的振动状况。因此，模态分析是研究传动系统动力特性的基础，为确定其使用环境和工作状态提供理论依据[4-5]。

传动系统模态分析就是计算特征值和特征向量，即假设系统在无阻尼及外载荷状态下求解自由振动的模态矢量。对于1个无阻尼系统，其振动方程可以用矩阵形式表示[6]

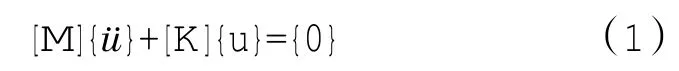
式中：[μ]为位移向量；[M]为质量矩阵；[K]为结构刚度矩阵，可包含预应力的影响。

为求式（1）所表示的系统动力特性，可将其改写为

式中：ω为系统圆频率。

这是1个求解特征值的问题，最多可以求得n个ω及其相对应的振型，均满足式（1），n为自由度数。求解式（2）通常可用跟踪法、变换法、Lanczos法等。对于传动系统，由于其计算量较大，因而考虑使用Lanczos法求解系统的各阶模态[7-8]。

2　传动杆模态计算

传动杆结构如图1所示。其中间设有刚度可变的辅助支承轴承，传动杆两端分别通过花键与齿轮连接。齿轮通过轴承支承于齿轮箱内，并与传动杆一同构成转子系统。

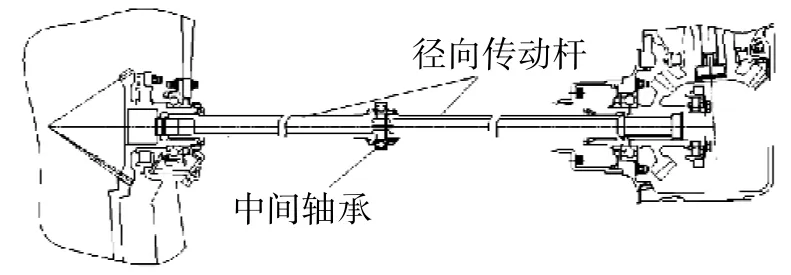
图1 传动系统结构

2.1转子模态计算

使用传统方法计算传动杆模态通常只考虑传动杆及与其相连的转动部件，而忽略轴承和支承结构，并在支承处以等效刚度代替。建立有限元模型如图2所示。其中1、5支点为滚棒轴承，需提供径向刚度；2、3、4支点为球轴承，需提供轴向、径向刚度[9-10]。

图2 传动杆有限元模型

1～5支点是由轴承与支承结构共同构成的支承系统，因此可将其视为2个串联的弹簧，利用式（3）可计算整个支承系统在轴、径向的支承刚度，并以此作为传动杆模态计算所用的等效刚度。

式中：k为支承系统刚度；k1为轴承刚度；k2为支承结构刚度，单位均为N/mm。

轴承刚度的计算方法为

式中：kbr为球轴承径向刚度，N/mm；kba为球轴承轴向刚度，N/mm；krr为棒轴承径向刚度，N/mm；Fr为轴承径向力，N；Fa为轴承轴向力，N；n为轴承滚子数量；d为轴承滚子直径，mm；L为棒轴承滚子长度，mm。

根据传动系统结构及所传递的载荷计算得到各轴承支承所受径、轴向载荷，结合轴承结构参数按式（4）～（6）可分别计算球、棒轴承的各向支承刚度，计算结果见表1。

通过有限元计算可得支承结构刚度，结合由式（4）～（6）计算可得轴承刚度，并利用式（3）可得传动杆各支点等效刚度，见表2。

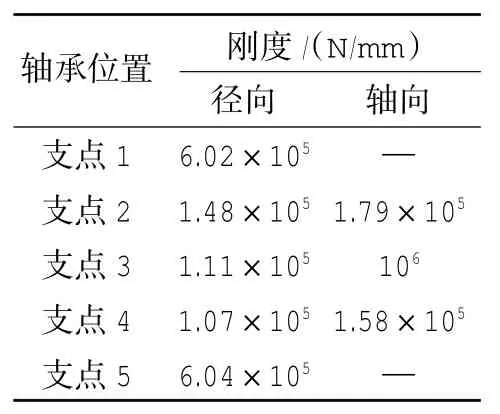
表1 轴承刚度计算结果

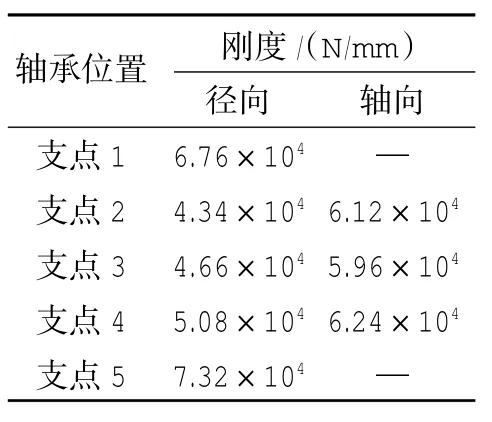
表2 等效支承刚度

在图2中各位置建立弹簧单元，并将表2中的各向刚度代入，经过模态计算可得各阶频率及振型，计算结果如图3所示。

2.2系统模态计算

为获得更精确的传动杆动态特性结果，需同时考虑其附属结构及支承结构。因此，将齿轮箱（含齿轮）、传动杆、辅助支承装置一同加以考虑，建立完整的传动系统模型，如图4所示。可先分别针对系统中的零件（齿轮箱、齿轮、传动杆等）建立有限元模型，后根据系统的装配关系，在各零件的连接位置建立弹簧元，并赋予合适的刚度[11-13]。

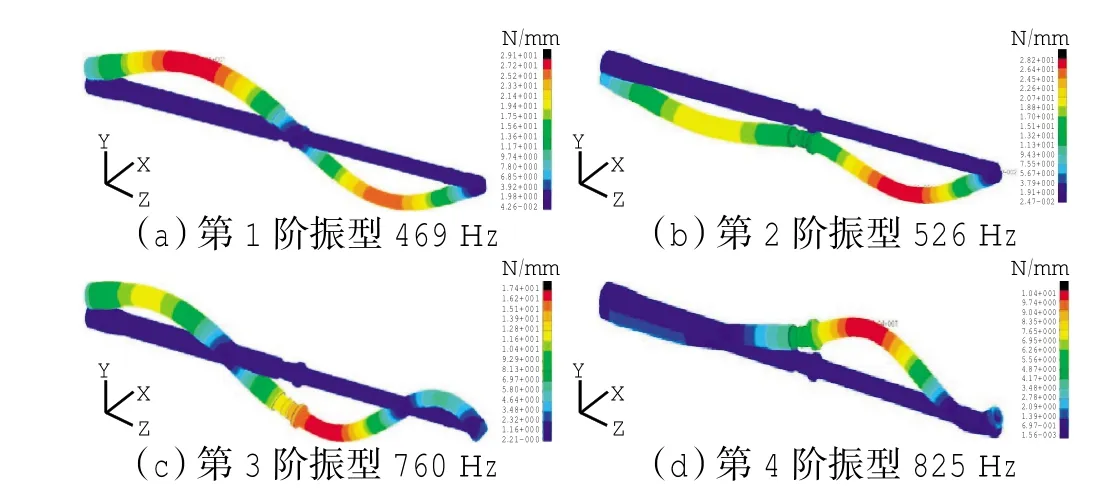
图3 转子计算传动杆各阶模态

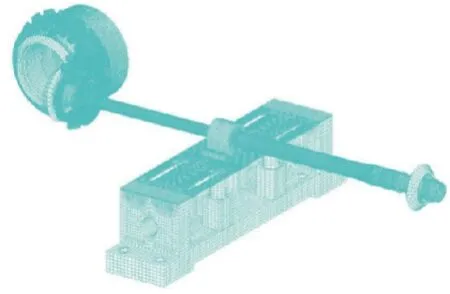
图4 有限元模型

与前文所述简化模型相比，系统模型在各连接刚度取值方面有所不同。由于系统模型中详细描述了支承结构的特性，因此不需要使用表2中的等效支承刚度，仅需在转、静子件，即传动杆转子及其支承之间以弹簧元的形式模拟轴承的刚度。通常可在每个轴承位置建立径向弹簧，对于球轴承还需建立轴向弹簧，弹簧刚度见表1。

此外，在齿轮啮合处还应建立弹簧元模拟齿轮的啮合刚度，该啮合刚度将主、从动齿轮的动态特性相互关联，相当于在传动杆的输入齿轮端附加了质量，起到了约束的效果，降低了传动杆的固有频率，对低频模态的作用更为明显。所以，啮合刚度对整个系统模态计算起到了非常重要的作用。对于一般模态计算可使用平均啮合刚度进行线性计算，其刚度取值可依照文献[14]所述方法，并结合主、从动齿轮的轮齿齿面参数计算得到。

经过模态计算可得各阶频率及振型，计算结果如图5所示。

3　传动杆模态试验验证

3.1试验方案

将传动杆安装在如图6所示的试验台上，传动杆两端分别连接主动、负载齿轮箱。安装完毕后，进行同轴度测量，确保主动、负载齿轮同轴度不大于0.10mm。

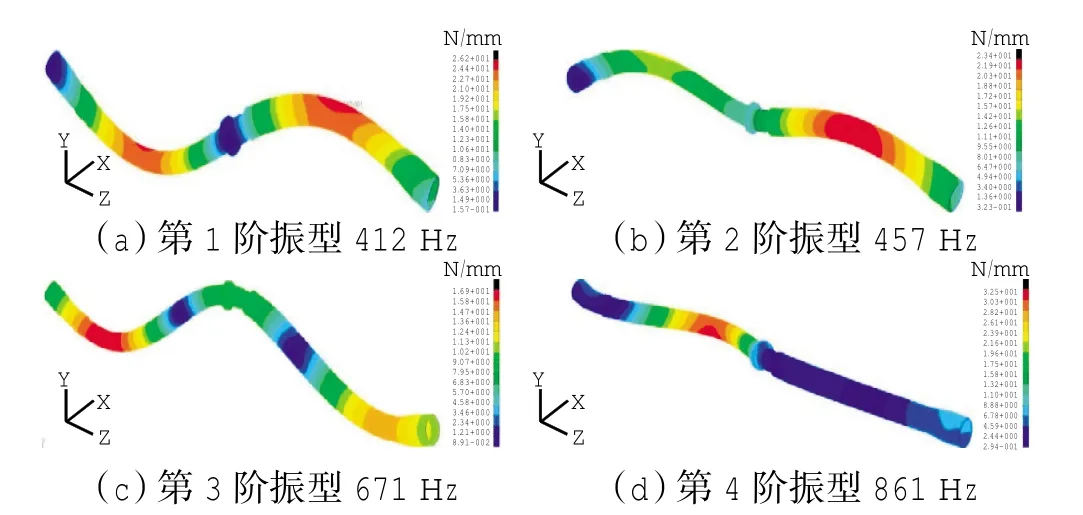
图5 系统计算传动杆各阶模态

使用LMS模态分析软件及数据采集装置进行传动杆模态测试[6-8]，并按图7所示连接设备。采用线单元建模模拟，采用笛卡尔坐标系统建立节点模型。根据测量所得的几何尺寸参数建立节点模型，如图8所示。

应用LMS软件中的ModalAnalysis模态分析模块对试验数据进行分析，经几何模型加载、模态数据选取和模态参数计算得到模态质量、模态刚度、模态阻尼等相关信息。试验模态分析计算原理如图9所示。

图6 试验台

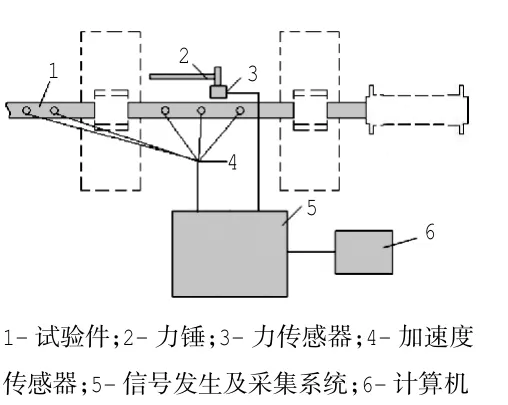
图7 模态测试

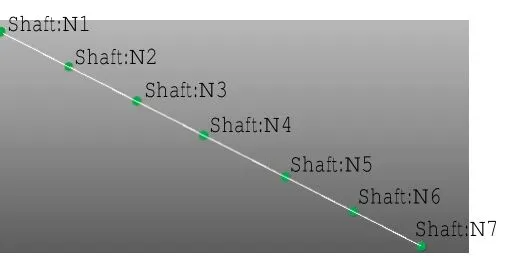
图8 传动杆试验测试模型

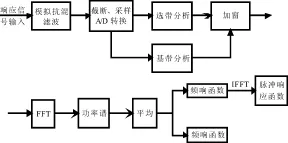
图9 模态分析计算原理

3.2测试结果

使用锤击法测量传动杆模态[15-16]，得到敲击点附近数据采集点频响函数曲线，如图10所示。由于主要关注传动杆的径向振动状态，未给出数据采集点轴向的频响函数曲线。对测试数据进行分析，获取传动杆弯曲振动信息，获得传动杆的各阶模态和振型，如图11所示。

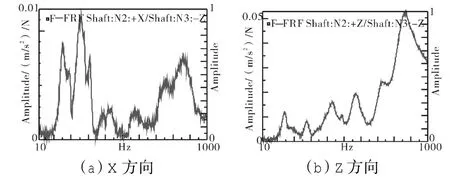
图10 数据采集点频响函数曲线

图11 传动杆各阶模态

3.3结果分析

从图5、11中可见，有限元计算和试验测试得到的前4阶模态振型一致，对使用有限元方法计算和试验测试的传动杆各阶模态结果进行对比，结果见表3。

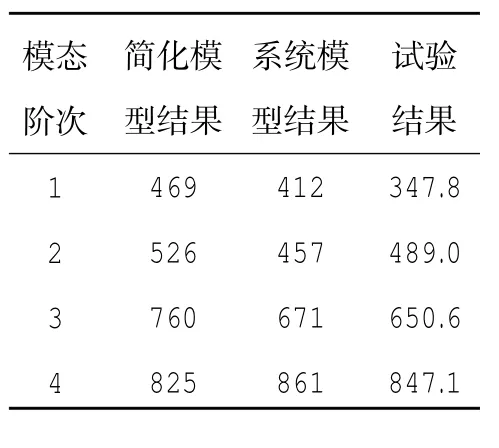
表3 模态试验结果对比Hz

通过对比可知，采用简化模型的模态计算结果前3阶频率与试验结果相差较大，使用系统模型计算能获得与试验较为一致的结果，但无论使用简化模型或者系统模型计算得到的第1阶弯曲模态均与试验结果存在一定差异。原因在于：模态试验是在如图6所示的试验台上进行的，系统中存在花键、轴承等包含阻尼的元件，锤击所产生的能量不足以克服这些阻尼，导致试验所得到的低频模态误差较大，置信度较低；随着系统响应频率的提升，阻尼的作用逐渐减弱，从而得到令人满意的结果。

此外，简化模型的计算结果与系统模型的计算结果存在较大差异，使用系统模型计算能得到更接近于实际的模态结果。由于简化模型既未考虑附加在传动杆上支承结构的质量，又未考虑实际安装状态下在支承位置处的刚度，因此在低频部分获得了较高的固有频率；随着固有频率的提高，附加在传动杆上的质量影响逐渐减小，从而能在高频处与试验结果具有较高的一致性。通常，对传动杆的动力性能计算主要关注其低阶模态，为获得较为准确的各阶固有频率，必须考虑将支承结构的质量附加于计算模型之上。但会带来很多前置工作量，且计算作用于传动杆上的附加质量较为繁琐，同时也是一种近似，因而直接进行传动系统模态计算显得相对便捷，且能获得较高的计算精度，特别是对于重点考察的低频部分，能真实反映系统的固有特性，为后续动力特性计算提供良好的基础。

4　结论

（1）无论简化模型还是系统模型，计算所得的各阶模态振型与试验结果较为吻合，且模型所包含的信息越详细，吻合度越高；

（2）在低频部分，与传动杆相连的结构质量会对计算结果产生较大影响，从而使简化模型和系统模型的计算结果产生较大差异；

（3）建立系统模型能较好地反映传动杆的真实动力性能，但会增加计算成本；

（4）由于系统中存在花键、轴承等连接结构，测试结果在高频部分的真实性有所下降，后期需对连接结构对系统动力特性的影响开展试验研究，提高试验结果的可信度。

参考文献：

[1]付才高.航空发动机设计手册：第19册[M].北京：航空工业出版社，2000：57-71. FU Caigao.Aircraft engine design manual：19th album [M].Beijing：Aviation Industry Press，2000：57-71（.in Chinese）

[2]郭梅.航空发动机中央传动杆磨损故障分析与研究[J].燃气涡轮试验与研究，2013（2）：54-58. GUO Mei.Investigation on radial driving shaft failure for an aeroengine [J].Gas Turbine Experiment and Research，2013（2）：54-58（.in Chinese）

[3]林基恕.航空燃气涡轮发动机机械系统设计[M].北京：航空工业出版社，2005：119-146. LIN Jishu.Mechanic system design of aeroengine [M].Beijing：Aviation Industry Press，2005：119-146（.in Chinese）

[4]王勖成.有限单元法[M].北京：清华大学出版社，2003：468-518. WANG Xucheng.Finite element method[M].Beijing：Tsinghua Univer-sity，2003：468-518（.in Chinese）

[5]马永列.结构模态分析实现方法的研究[D].杭州：浙江大学，2008. MA Yonglie.The research of structure modal analysis realization[D]. Hangzhou：Zhejiang University，2008.（in Chinese）

[6]孙海东，傅强.航空发动机振动监测研究[J].机械设计与制造，2007 （2）：127-129. SUN Haidong，FU Qiang.Research on vibration monitoring of aero-engine[J].Machinery Design and Manufacture，2007（2）：127-129.（in Chinese）

[7]王俨剀，王理，廖明夫.航空发动机整机测振中的基本问题分析[J].航空发动机，2012，38（3）：49-53. WANG Yankai,WANG Li,LIAO Mingfu.Analysis of basic problems for aeroengine vibration measurement [J]. Aeroengine，2012，38（3）: 49-53.（in Chinese）

[8]张宝诚.航空发动机试验和测试技术[M].北京：北京航空航天大学出版社，2005：280-282. ZHANG Baocheng.Experiment and testing technology of aeroengine [M].Beijing：Beihang University Press，2005：280-282.（in Chinese）

[9]程小勇.航空发动机转子系统模拟支承设计与刚度计算[J].航空计算技术，2012，42（6）：9-12. CHENG Xiaoyong. Rotor support simulation design and equivalent stiffness computation for aeroengine [J].Aeronautical Computing Technique，2012，42（6）：9-12.（in Chinese）

[10]洪杰.转子支承动刚度对转子动力特性的影响分析[J].航空发动机，2008，34（1）：24-27. HONG Jie.Effects of dynamicsstiffness of rotor bearing on rotor dynamic characteristics [J].Aeroengine，2008，34（1）：24-27.（in Chi-nese）

[11]欧园霞，李彦，尹泽勇，等.航空发动机整机模态计算分析[J].航空动力学报，1994，9（2）：137-141. OU Yuanxia，LI Yan，YIN Zeyong，et al.Vibration mode analysis for a complete areoengine [J]. Journal of Aerospace Power，1994，9（2）：137-141.（in Chinese）

[12]王海涛.某型航空发动机整机振动特性分析[D].南京：南京航空航天大学，2010. WANG Haitao.Research on whole body vibration of aerongine[D]. Nanjing：Nanjing University of Aeronautics & Astronautics，2010.（in Chinese）

[13]晏砺堂，朱梓根，宋兆泓.结构系统动力特性分析[M].北京：北京航空航天大学出版社，1989：35-41. YAN Litang，ZHU Zigen，SONG Zhaohong. Dynamic characteristic analysis of structure system [M].Beijing：Beihang University Press，1989：35-41.（in Chinese）

[14]方子帆.齿轮传动多体接触动力学模型[J].机械传动，2009（1）：15-18. FANG Zifan.Multi-body contact dynamic modeling of gear transmission [J].Journal of Mechanical Transmi-ssion，2009（1）：15-18.（in Chinese）

[15]李勋.锤击法在航空发动机部件模态试验中的常见问题浅析[J].航空发动机，2010，36（5）：47-51. LI Xun.Common problems analysis of impact modal test in aero-engine component[J].Aeroengine，2010，36（5）:47-51.（in Chinese）

[16]杨炳渊.应用锤击法的全弹模态试验[J].上海航天，1990（1）：41-46. YANG Bingyuan, Elastic modal test using hammering method[J]. Aerospace Shanghai，1990（1）：41-46.（in Chinese）

（编辑：栗枢）

Dynamic Characteristics Study on Transmission Rod with High Speed and Large Aspect Ratio

GUO Xia，ZHANG Huan-zhang，CHENG Xiao-yong，WAN G Shao-bo
（AVIC Commercial Aircraft Engine Co.,Ltd.，Shanghai 201108，China）

Abstract:The radial drive shaft of commercial aeroengine has the characteristics of large draw ratio and high rotate speed.In order to ensure its reliability,it is necessary to accurately processa dynamic characteristic analysis,in which the boundary conditions make huge sense.Simplified and integrated models were respectively used to analyze the mode of radial drive shaft.By setting the boundary conditions, the dynamic characteristics analysis was processed and the models were verified.The results of comparison show that the modal vibration shape calculated by integrated model is more consistent with the experimental,which demonstrates the correctness of boundary conditions choosing method.

Key words:driveshaft；dynamic characteristics；mode；finite element；experimental verification

中图分类号：V233.1

文献标识码：A

doi：10.13477/j.cnki.aeroengine.2016.03.006

收稿日期：2015-12-23

作者简介：郭霞（1983），女，工程师，主要从事航空发动机总体结构设计工作：E-mail：157863417@qq.com.