1种发动机自适应模型的修正方法

杨天南，吴　森，王　征（.海军驻沈阳地区发动机专业军事代表室；.中国人民解放军驻沈阳黎明航空发动机集团（有限）责任公司军事代表室：沈阳0043）



1种发动机自适应模型的修正方法

杨天南1，吴森1，王征2
（1.海军驻沈阳地区发动机专业军事代表室；2.中国人民解放军驻沈阳黎明航空发动机集团（有限）责任公司军事代表室：沈阳110043）

摘要：为解决由于工艺落后和性能衰退所导致的发动机模型与实际发动机失配的问题，从而达到视情维修的目的，建立了1种基于遗传算法的自适应模型修正方法。利用遗传算法高效率的全局搜索能力，以发动机性能参数为目标，优化部件参数，实现了模型的修正，并通过分析发动机性能参数对部件参数的敏感性，研究了选取不同组合的待修正部件参数对模型修正精度的影响。结果表明：采用该修正方法所建立的发动机模型准确性高、鲁棒性强，且具有良好的通用性，为发动机的健康管理和故障诊断提供了重要依据，具有很好的军事和工程应用价值。

关键词：自适应模型；修正方法；健康管理；遗传算法；视情维修；航空发动机

引用格式：杨天南，吴森，王征.1 种发动机自适应模型的修正方法[J].航空发动机，2016,42（3）：98-102.YANG Tiannan,WU Sen,WANG Zheng.A correction method for aeroengine adaptive model[J].Aeroengine,2016,42(3):98-102.

0　引言

建立精确的航空发动机模型以准确掌握每台发动机性能变化的情况，对提高飞行品质和战备完好率有重要意义。然而由于发动机的制造和装配误差以及使用过程中部件磨损、性能蜕化等原因，使得模型与实际发动机失配，因此，必须对所建模型进行修正[1]。以发动机气路故障诊断为目的的非设计点模型自适应修正已经有很多学者研究过[2-4]。Stamatis等[5]介绍了修正系数法（MF，Modification Factors），并用广义最小残差法优化修正系数；Lambiris等[6]介绍了加权误差函数并使用了多种算法去优化修正系数；Stamatis 等[7]基于奇异值分解的方法，利用敏感度分析进行快速选择并对修正系数进行优化；Kong等分别利用比例缩放法[8]和基于遗传算法的压气机特性参数耦合方法[9]对发动机性能进行自适应计算。以上自适应修正方法在偏离设计点或者退化条件的假设下，都能使仿真性能与实际发动机很好地匹配。这种设计点的自适应方法通常需要选择一些部件的设计点参数来检验和改进。但实际上，因为发动机的构造极其复杂，往往缺乏足够的部件数据来估计发动机整机的设计点特性。

本文针对以上方法存在的问题，在基于某发动机部件级数学模型的基础上，建立了1种基于遗传算法的自适应修正模型，通过修正结果对修正模型的准确性、鲁棒性和通用性进行研究，证明了基于遗传算法的自适应修正模型方法的有效性。

1　遗传算法的基本原理及其自适应模型

遗传算法（Genetic Algorithm）是1975年由美国学者Holland提出的1种寻优算法，采用人工进化的方式对目标空间进行随机搜索[10-12]。其算法流程如图1所示。由于自适应模型的待修正参数选取较多，因此计算量很大，且容易陷入局部最优解；而遗传算法模拟自然进化过程，通过变异保证了种群的多样性，全局搜索能力强，不容易陷入局部最优解，容易得到全局最优解，且遗传算法生成种群后进行并行计算，搜索效率高，适用于自适应模型的修正。基于遗传算法的发动机模型的自适应修正在确定优化目标和待修正参数后，在所选搜索空间内随机生成待修正参数的种群，之后通过选择、交叉、变异的过程不断迭代，直到找到满足需要的解为止。

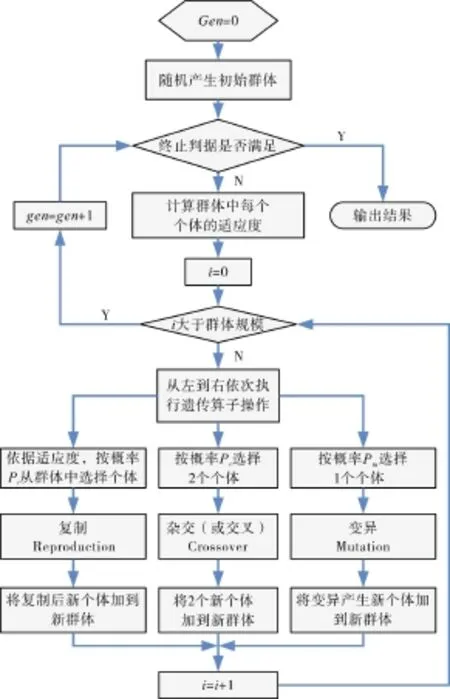
图1 遗传算法流程

将发动机性能1个状态点的自适应修正看作1个优化问题，如图2所示。由于发动机存在个体差异以及性能退化现象，因此实际上即使是同一型号的发动机其部件参数也存在很大差异，且在不同程度上偏离设计值。从图中可见，自适应模型修正过程为在线修正，在一定的环境和控制条件下，以最小化该点发动机的真实性能参数z0与模型计算的性能参数z的差值z-z为目标，修正得到的发动机模型的部件参数（即在空中工作时的真实参数），这对于发动机及其部件的健康管理和故障诊断具有较高价值。

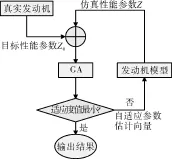
图2 基于遗传算法的自适应模型修正过程

当设计点操控条件下的测量参数z0作为目标性能参数时，任何潜在合适的部件参数x可以用目标函数来估计，目标函数定义为

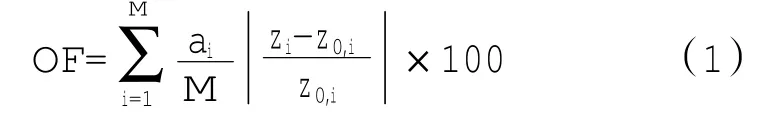
式中：z0,i为第i个目标性能参数的实际值；zi为第i个目标性能参数的模型计算值；ai为考虑一些不确定因素以及目标参数的相对重要性的权值。本文不考虑这些测量参数的不确定性，因此所有目标性能参数的权重都相等，即

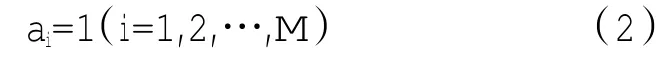
定义遗传算法中的个体的适应度函数为

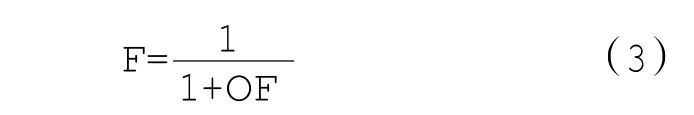
式中：目标函数OF由式（1）定义。适应度函数在0～1之间，1为最优，0为最差，表示预测性能参数和实际性能参数的差异。

遗传算法中每次交叉和变异的操作主要由指派给这些操作的概率决定，计算的结果和搜索速度由群体的大小所决定。基因代数越多、群体越大则计算结果的精度越好，但是需要牺牲计算速度[13]。因此有必要在多次试验比较后决定遗传算法中的参数设置。

当遗传算法中的参数值设置较小时，可以帮助算法快速找到正确的搜索空间，而参数值设置较大有利于算法找到最优值。遗传算法中的参数选择需要视具体问题而定，本文中遗传算法参数设置是变化的，其初始参数和计算结束时的参数不相同，具体参数设置见表1。

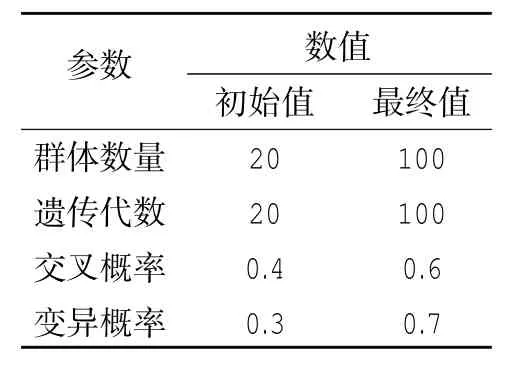
表1 遗传算法的参数设置值

从表中可见，给定待修正的自适应参数的上下限，以保证算法在正确的空间中搜索，以得到最优值。在最初的试探计算中，需要反复试验来校正自适应参数值的上下限。

2　待修正参数的选择及其敏感性分析

恰当的选择待修正的部件参数对自适应模型的求解有着十分重要的意义，在选择待修正的部件参数时需考虑以下重要因素[14-15]：

（1）所选择的待修正的部件参数必须与目标性能参数有很强的关系。否则在修正的过程中没有足够的搜索空间，不能搜索到更优的修正结果。

（2）待修正部件参数的个数没有限制，但是待修正参数选择的不同其修正效果也不同。而且，待修正部件参数的个数选择越多，搜索空间越大，所获得的修正结果越接近目标参数。

（3）待修正部件参数的上下限同样决定了搜索空间范围。因此，在自适应修正过程中，选择合适的参数上下限十分重要，这可能需要多次试验来确保最优值包含在搜索空间中。

依据以上3项原则，所选择的目标性能参数见表2，待修正部件参数见表3。1个型号发动机的部件参数可以从工程制造或公开的资料中获得，但由于制造、装配公差和健康状况等因素，每台发动机的真实部件参数都会有所差异，因此最初获得的初值不一定是合适的。

表2 目标性能参数

为了选择最合适的待修正参数组合，首先对所有待修正参数进行目标参数的敏感性分析。保持其他待修正部件参数不变，每次仅改变1个待修正部件参数值，使其增大1%，进行发动机部件级模型计算，就可得到目标性能参数对该部件参数的变化量，如图3所示。

表3 待修正的部件参数

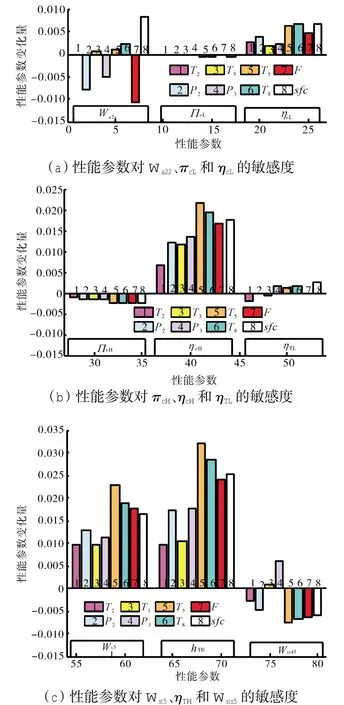
图3 性能参数对9个部件参数敏感度对比

从图中可见，目标性能参数随着部件参数的改变有不同的变化，其敏感程度同样因部件参数不同而有显著不同。例如：T5、T8、F和sfc对ηTH的变化有强烈反映，而所有的目标性能参数对πcI的变化反映十分平淡。因此，在自适应模型修正中，倾向于选择那些对目标性能参数敏感性强的部件参数。对单个待修正部件参数变化引起的各目标性能参数变化率求和，并进行归一化处理，得到性能参数对修正部件参数的敏感度，如图4所示。

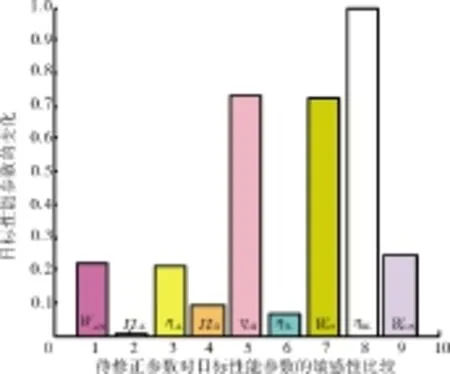
图4 性能参数对待修正参数总的敏感度

待修正部件参数初值的选择，需要匹配基本的发动机模型以便进行特性参数仿真。待修正部件参数初值的给定，需要使预测的目标性能参数尽可能接近真实值，以得到更准确的自适应修正模型。

3　不同组合的待修正参数的自适应模型

对于同1个发动机模型、同样的目标性能参数，当选择不同的待修正部件参数的组合时，会导致自适应模型的修正精度不同。

为了分析待修正部件参数不同组合的影响，根据图3、4的敏感性分析结果，设置了3组待修正参数的组合（表3）。其中，组合A包括了所有的待修正部件参数，组合B选择了6个对目标性能参数敏感的部件参数，组合C选择了3个对目标性能参数最敏感的部件参数。仍以表2中的参数作为目标性能参数，用基于遗传算法的自适应修正模型分别对表3中的3种待修正部件参数组合（组合A、B、C）进行修正计算。经过3种不同待修正部件参数组合修正后，得到待修正部件参数相对于初始值的偏差量，如图5所示；3种组合修正得到目标性能参数偏差量，如图6所示。从图6中可见，修正后的目标性能参数比未经修正的目标性能参数有明显改善；3种组合的适应度函数值比较如图7所示。从图中可见，组合A的修正效果最好，而组合C的修正效果最差。

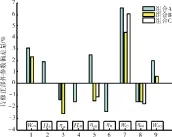
图5 3种组合修正部件参数偏差量

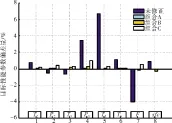
图6 3种组合修正得到目标性能参数偏差量

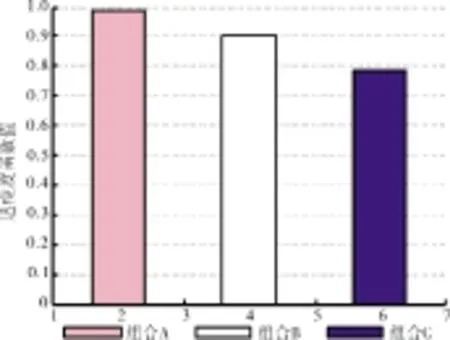
图7 3种组合的适应度函数值比较

不同待修正参数的组合会导致修正效果有一定差别，合适的参数组合能使修正后的目标性能参数十分接近于实际值。从图6中可见，组合A目标性能参数最大偏差值低于0.5%，优于组合B和C的；从图7中可见，组合A的适应度函数值可以达到0.99，优于组合B和C的。

在基于遗传算法的自适应修正模型中，没有严格选择待修正部件参数方法，因为该模型的鲁棒性较好，只要待修正部件参数选择合适，都可以计算出较接近于实际值的结果。图6、7可以说明：模型的计算结果的好坏取决于待修正参数的选择和参数上下限的给定值。

每个待修正部件参数的搜索空间必须能覆盖最优解，这样才能保证模型能够搜索到目标性能参数最接近实际值。以待修正部件参数初始值为中心的90% ~110%作为待修正参数的初始上下限，反复测试上下限以确保待修正参数的最终结果能在上下限之间。

遗传算法属于1种随机搜索算法，因此基于遗传算法的自适应修正模型即使在相同参数设置下，每次计算结果也不会完全相同。为了确保模型计算结果的准确性，需要对同样参数设置的程序运行10次。以组合A为例，运行10次程序，得到的适应度函数值有9次在0.97～0.99之间，目标性能参数值也十分接近，只有1次运行的适应度函数值为0.94，多次计算的模型适应度函数值如图8所示。从图中可见，基于遗传算法的自适应修正模型可以得到可靠结果，具有很强的鲁棒性。

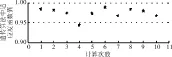
图8 10次计算的模型适应度函数值

4　结论

建立了针对单个状态点的修正模型，即基于遗传算法的自适应修正模型，并通过发动机性能参数对部件参数的敏感性分析，研究了待修正部件参数选择组合对模型修正效果的影响。仿真结果证明，基于遗传算法的自适应修正模型的精确性和鲁棒性很好、通用性好，适用于发动机模型的自适应修正，对发动机故障诊断和健康管理具有很好的工程价值。

参考文献：

[1]Link C J，Jack D M.Aircraft engine controls：design，system analysis and health monitoring[M].Alexander：American Institute of Aeronautics and Astronautics，2009：118-124.

[2]王永华，李冬.基于云粒子群算法的航空发动机性能衰退模型模型研究[J].燃气涡轮试验与研究，2012，25（1）：17-19. W ANG Yonghua，LI Dong.Research on aero-engine performance dete-rioration model based on the cloud particle swarm optimization [J]. Gas Turbine Experiment and Research，2012，25（1）：17-19.（in Chinese）

[3]郭玉明，陈东林，王宇.某型涡喷发动机状态空间模型的提取与修正研究[J].航空精密制造技术，2009，45（6）：21-23. GUO Yuming，CHEN Donglin，W ANG Yu.Research for the distillation and modification of aero engine state space model[J].Aviation Precision Manufacturing Technology，2009，45（6）：21-23.（in Chinese）

[4]郑铁军，王曦，李秀芹，等.建立航空发动机状态空间模型的修正方法[J].推进技术，2005，26（1）：46-49. ZHENG Tiejun，W ANG Xi，LI Xiuqin，et al.Modified method of estab-lishing the state space model of aero engine [J].Journal of Propulsion Technology，2005，26（1）：46-49（.in Chinese）

[5]Stamatis A，Mathioudakis K，Papailiou K D.Adaptive simulation of gas turbine performance [J].Journal of Engineering for Gas Turbines and Power，1989，112（2）：168-175.

[6]Lambiris B，Mathioudakis K，Stamatis A，et al.Adaptive modeling of jet engine performance with application to condition monitoring[J].Journal of Propulsion and Power，1994，10（6）：890-896.

[7] Stamatis A，Mathioudakis K，Papailiou K.Optimal measurement and health index selection for gas turbine performance status and fault di-agnosis [J]. Journal of Engineering for Gas Turbines and Power，1992，114（2）：209-216.

[8] Kong C，Ki J，Kang M.A new scaling method for component maps of gas turbine using system identification [J].Journal of Engineering for Gas Turbines and Power，2003，125（1）：639-646.

[9]Kong C，Kho S，Ki J.Component map generation for a gas turbine using Genetic Glgorithms[J].ASME Turbo Expo：Power for Land，Sea，& Air，2004，128（1）：469-474.

[10]崔文斌，叶志锋，彭利方.基于信息融合遗传算法的航空发动机气路故障诊断[J].航空动力学报，2015，30（5）：1275-1280. CUI W enbin，YE Zhifeng，PENG Lifang.Aero-engine gas path fault diagnosis based on Genetic Algorithm of information fusion[J].Journal of Aerospace Power，2015，30（5）：1275-1280.（in Chinese）

[11]李秋红，孙健国.基于遗传算法的航空发动机状态变量模型建立方法[J].航空动力学报，2006，21（2）：427 -431. LI Qiuhong，SUN Jianguo.Aero-engine state variable modeling based on the Genetic Algorithm [J].Journal of Aerospace Power，2006，21 （2）：427-431.（in Chinese）

[12]Ganguli S，Deo S，Gorinevsky D.Parametric fault modeling and diag-nostics of a turbofan engine [J].IEEE International Conference on Control Applications，2004，1（1）：223-228.

[13]Li Y G，Pilidis P.GA-based design-point performance adaptation and its comparison with ICM-based approach [J]. Applied Energy，2010，87（1）：340-348.

[14]李立君，尹泽勇，乔渭阳.基于多目标遗传算法的航空发动机总体性能优化设计[J].航空动力学报，2006，21（1）：13-18. LI Lijun，YIN Zeyong，QIAO W eiyang.Performance optimal design of aircraft engine based on multi-objective Genetic Algorithm [J].Journal of Aerospace Power，2006，21（1）：13-18.（in Chinese）

[15]陈永琴，苏三买.自适应变搜索域遗传算法及其在发动机模型中的应用[J].推进技术，2007，28（4）：428-432. CHEN Yongqin，SU Sanmai.Adaptive variable search scope Genetic Algorithm and its application in aero-engine mathematical model[J]. Journal of Propulsion Technology，2007，28（4）：428-432.（in Chinese）

（编辑：张宝玲）

A Correction Method for Aeroengine Adaptive Model

YANG Tian-nan1，WU Sen1，WANG Zheng2
（1.Navy Military Representative Office of Engine in Shenyang Area；2. Representative Office of PLA in Shenyang Liming Aeroengine Group Corporation Ltd.:Shenyang 110043，China）

Abstract:In order to solve the engine models mismatching the actual engines due to backward crafts and performance degradation，which calls condition maintenance, a correction method based on Genetic Algorithm for aeroengine adaptive model was proposed.W ith the efficient global search ability of Genetic Algorithm,the model was corrected by optimizing the component parameters when the performance parameters of the engine were chosen as the optimization objective.The effect of choosing different component parameter combinations on model correction accuracy was discussed by analyzing the sensitivity of engine performance parameters when the component parameters changed.The results show that the engine models have the advantages of high-accuracy,good robust performance and commonality by the method.It provides an important basis for engine health management and fault diagnosis,and has a very high military and engineering practice value.

Key words:adaptive model;correction method;health management;Genetic Algorithm;condition maintenance;aeroengine

中图分类号：V235.13

文献标识码：A

doi：10.13477/j.cnki.aeroengine.2016.03.019

收稿日期：2015-12-18基金项目：燃气轮机工程研究项目资助

作者简介：杨天南（1987），男，工程师，主要从事舰船燃气轮机和航空发动机故障诊断、测量、维修与全寿命保障等方面的研究工作；E-mail：ytn510bmw@163.com。