GPS动态变形分析中的傅里叶级数恒星日滤波
段海东 张献州 马 龙 李祖来张 拯 张正国 罗 奕
1 西南交通大学地球科学与环境工程学院,成都市犀安路999号,611756 2 高速铁路运营安全空间信息技术国家地方联合工程实验室,成都市犀安路999号,611756 3 成都铁路局成都高铁工务段,成都市荷花池路3号,610000
GPS动态变形分析中的傅里叶级数恒星日滤波
段海东1,2张献州1,2马龙1,2李祖来1,2张拯1,2张正国3罗奕3
1西南交通大学地球科学与环境工程学院,成都市犀安路999号,611756 2高速铁路运营安全空间信息技术国家地方联合工程实验室,成都市犀安路999号,611756 3成都铁路局成都高铁工务段,成都市荷花池路3号,610000
摘要:针对恒星日滤波中计算GPS卫星轨道运行周期提前时间的问题,提出一种基于傅里叶级数曲线拟合的提前时间估计方法。根据跨度达8 526 d的广播星历计算每天中所有可用卫星运行周期相对于前1 d的平均提前时间,将此平均提前时间作为采样点,以8阶三角函数形式展开的傅里叶级数进行曲线拟合,将卫星运行周期的提前时间拟合成关于时间的单一变量函数,免去了繁琐的计算步骤。实验结果表明,傅里叶级数恒星日滤波法缩小了监测点N、E、U三个方向坐标残差序列的均方根值,有效消除了GPS动态变形监测分析中的多路径影响,提高了复杂工程环境下动态变形监测中变形信息提取的能力。
关键词:GPS动态变形监测;恒星日滤波;广播星历法;傅里叶级数;曲线拟合
近年来,高频甚至超高频GPS接收机不断出现,提升了复杂工程环境下变形监测的实时动态监测能力。多路径影响是制约GPS精密动态变形监测技术发展的关键因素之一,干扰了动态变形信息的提取过程[1-2]。恒星日滤波利用GPS卫星运行的重复性特点,将低通滤波之后的坐标残差经过时间平移进行差分运算,消除两天之间具有相关性的误差,包括多路径误差[3-6]。开普勒轨道条件下,卫星重复出现在同一位置的时间应该比前1 d提前236 s,但是美国国防部并未将卫星的轨道周期约束为恒星周期,而是把地面跟踪站设定为固定站,所以卫星每天的实际轨道并不完全一致[6]。Choi等[1,7]在2004年通过对卫星轨道的分析证明,GPS卫星几何重复周期略小于恒星日,即卫星较前1 d重复出现在同一位置的时间提前量略大于236 s,约为245 s。本文采用开普勒第三运动定律计算GPS卫星运动周期及其变化情况,将此变化通过三角函数形式的傅里叶级数进行曲线拟合[8-9],以此对恒星日滤波进行修正,然后将修正后的恒星日滤波应用于GPS动态变形监测中,以便正确提取变形体的变形信息。
1广播星历法计算卫星轨道周期的统计规律
本文选取1992-02-12~2015-06-16跨度达8 526 d的GPS广播星历,覆盖了40颗卫星,包括32颗常用卫星(PRN1~PRN32)和8颗非常用卫星(PRN47、PRN65、PRN68、PRN69、PRN73、PRN76、PRN79、PRN80,因这8颗非常用卫星只在1992-08-04、08出现,故不予考虑),以广播星历法计算卫星重复出现的提前时间。
1.1广播星历法计算卫星重复出现提前时间的正确率
以236~254 s作为提前时间的合理波动范围,检验广播星历法计算提前时间的正确率(表1)。
由表1可见,在历元数目上,PRN3号卫星最多,而PRN32号卫星最少,分别为110 164个和39 765个。相应地,在广播星历法计算提前时间的正确数目上,PRN3号卫星也最多,而PRN32号卫星最少,分别为109 883个和37 081。但是,在计算正确率上,PRN19号卫星最高,而PRN29号卫星最低,分别为99.86%和83.63%。广播星历法计算32颗卫星重复出现提前时间的正确率平均值达到95.37%。
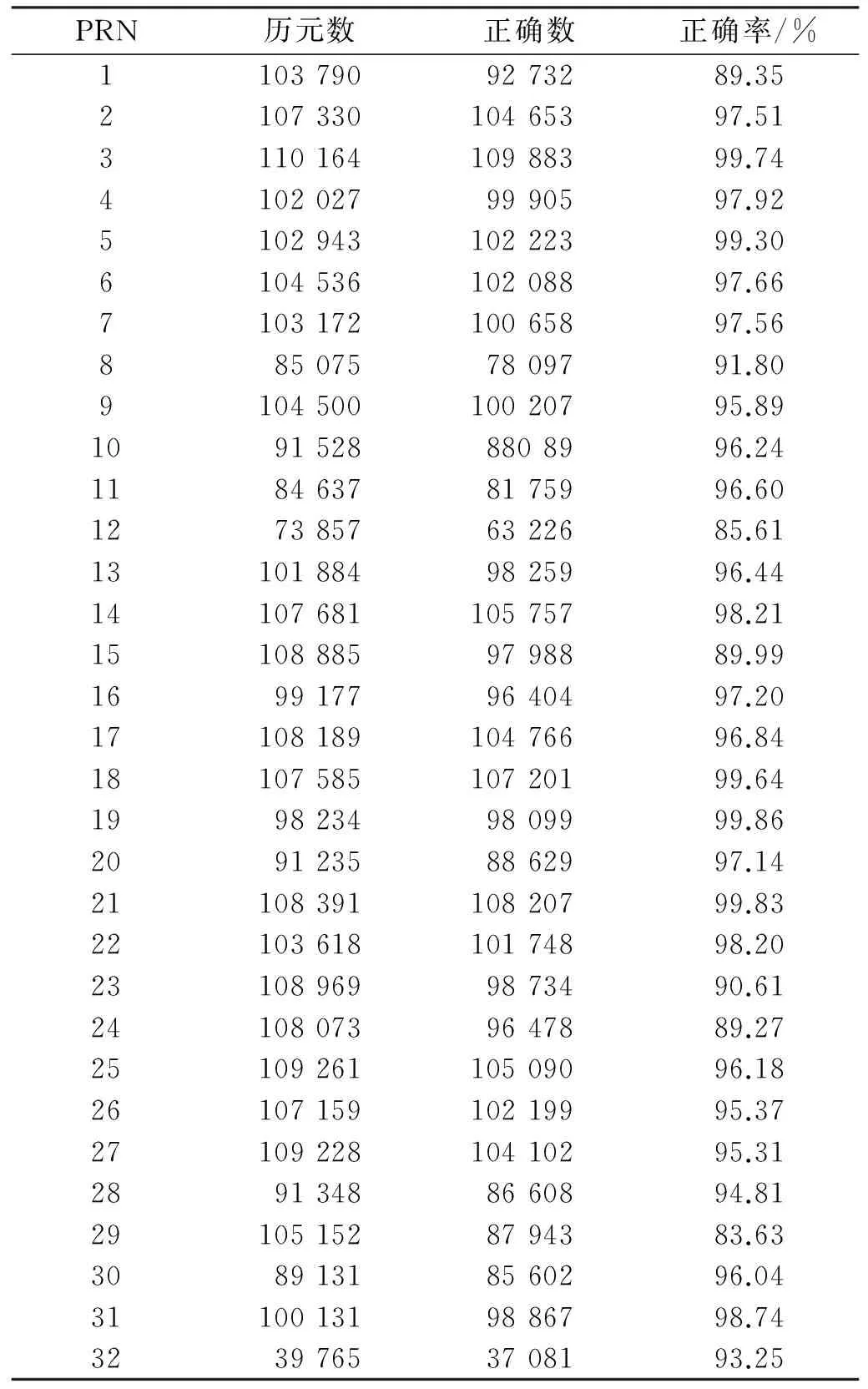
表1 广播星历法计算卫星重复出现提前时间的正确率统计
广播星历法计算卫星的重复出现提前时间存在一定的错误率,引起这一错误的原因包括地球非球形引力场摄动力、潮汐摄动力(包括地球固体潮、海潮、极移潮、负荷潮等)、日月及其他行星引力、太阳光压、地球反照压、地球辐射压、大气阻力、大气浮力、卫星本身热辐射压、姿态调整及变轨机动力、卫星退役等。当出现这种错误时需要使用其他方法进行计算,如最大互相关系数法、最小均方根误差值法等。
1.2卫星提前时间的分布
以波动在236 s~254 s范围内的每日平均提前时间作为竖轴、日期(1992-01-01~2016-01-01)为横轴作散点图。限于篇幅,只展示了PRN9、PRN17、PRN25共3颗卫星运行的日均提前时间散点分布情况(图1~3)。
由图1~3可见,广播星历法计算得到的32颗卫星的提前时间量不尽相同,单颗卫星在不同时期的提前时间也不相同。但是也不难看出:1)在大于1 a的时间跨度内,单颗卫星的提前时间在波动范围内具有一定的周期重复性,但每颗卫星的重复周期不尽相同,单颗卫星在不同时期内的重复周期也不尽相同;2)在1 a以下的时间跨度内,每颗卫星的提前时间具有一定的趋势性,但每颗卫星的趋势不尽相同,单颗卫星在不同时期内的趋势也可能不一样。
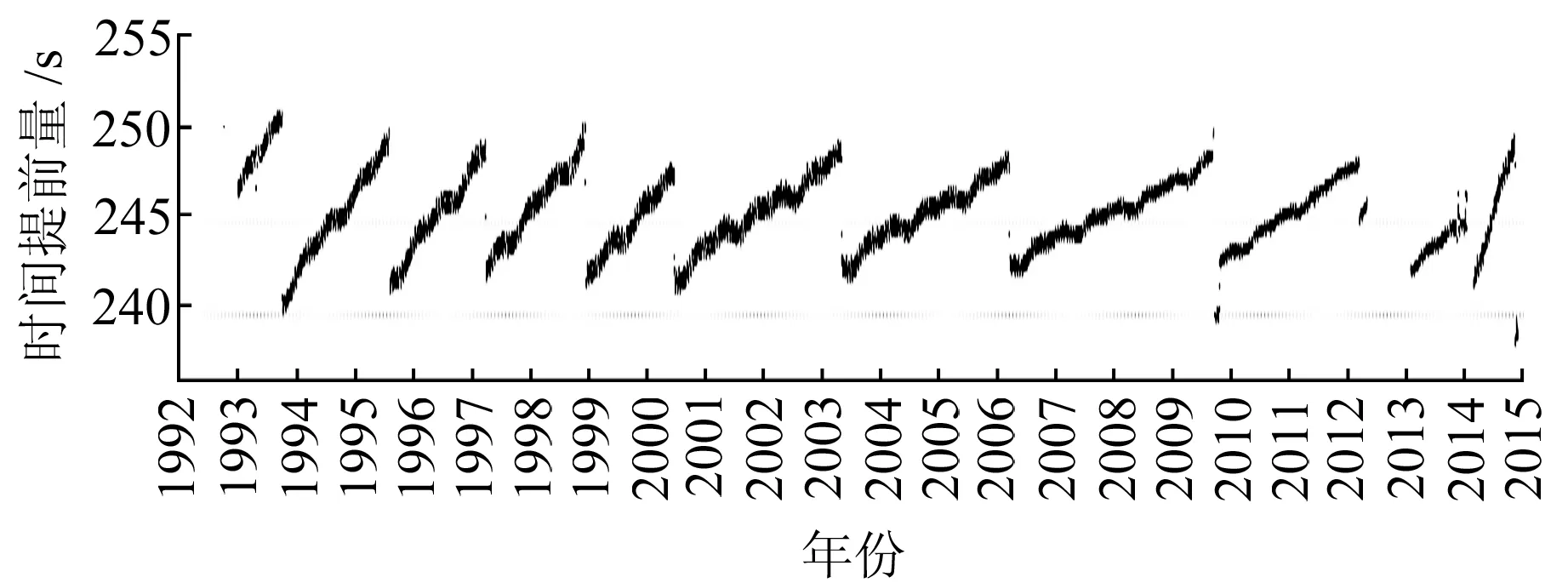
图1 PRN9号卫星的日均提前时间散点图Fig.1 Scatter of daily average preset time of PRN9

图2 PRN17号卫星的日均提前时间散点图Fig.2 Scatter of daily average preset time of PRN17
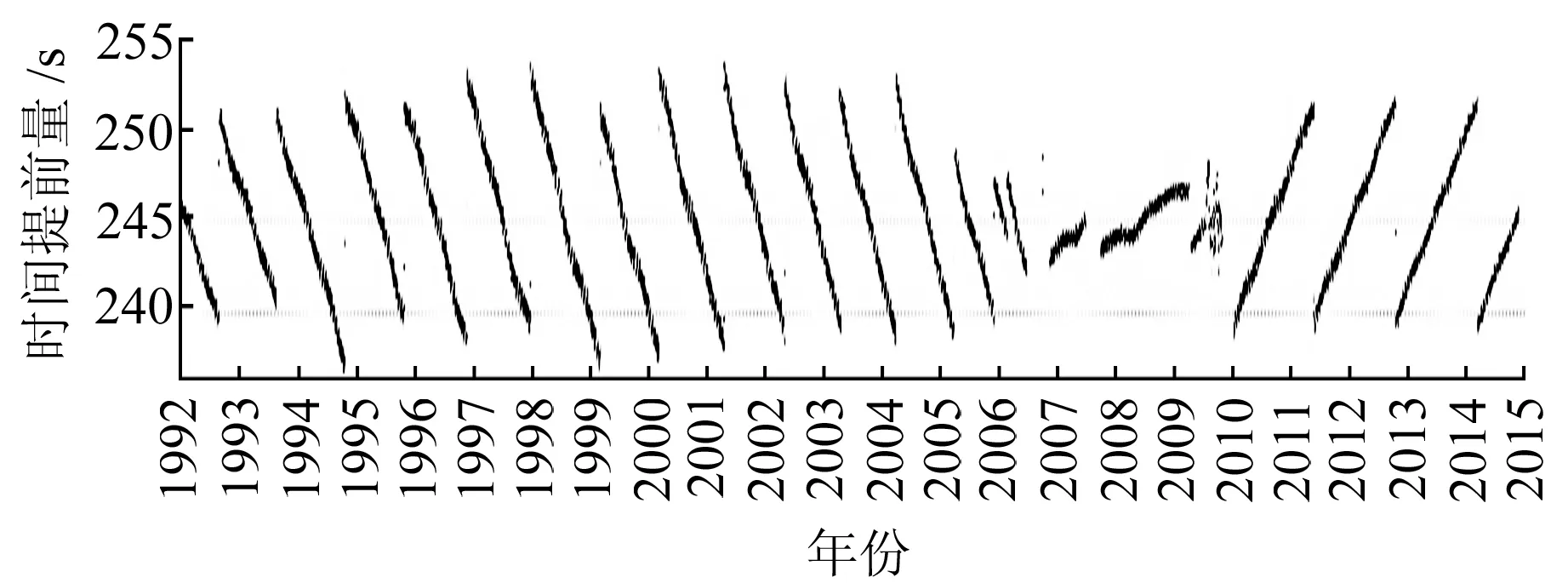
图3 PRN25号卫星的日均提前时间散点图Fig.3 Scatter of daily average preset time of PRN25
根据在短时间内卫星运行周期提前时间的趋势性,如遇到上文所述的广播星历法计算卫星运行周期提前时间出现错误时,可用插值法确定其正确的提前时间(简单的线性内插基本能够满足要求),也可以在短时间内对卫星运行周期的提前时间作出预测。
2卫星轨道周期提前时间曲线的函数拟合
将同1 d内所有可见卫星的日均提前时间进行均值运算,即为当日用于削弱多路径影响的坐标残差序列提前时间,图4中较细曲线即为日期-提前时间曲线。1992-02-12~2015-06-16每恒星日提前时间基本在244~247 s,提前时间随时间波动,呈现出一定的周期重复性。将提前时间用傅里叶1~8阶三角函数展开式进行最小二乘曲线拟合[8-9]。经计算,拟合残差在8阶时已经趋向收敛。同时,为了不增加过多的计算量,选取拟合残差最小的8阶傅里叶展开式作为拟合函数:
(1)
将1992-02-12作为时间起算原点,每恒星日作为1个采样间隔,每日的提前时间作为采样值,用傅里叶8阶展开式进行曲线拟合,在95%的置信水平下求得曲线拟合函数的参数,见表2。
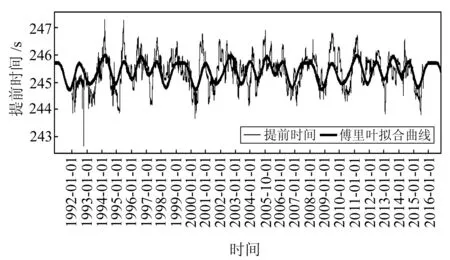
图4 提前时间及傅里叶拟合曲线Fig.4 Preset time and Fourier series curve fitting

参数参数值参数参数值参数参数值a0245.4000ω0.0021a1-0.1045b1-0.0047a2-0.0212b2-0.0238a3-0.0817b3-0.1551a4-0.0461b40.1003a5-0.0521b50.2606a6-0.1182b60.1414a70.0063b7-0.1518a8-0.1097b80.1532
拟合均方根误差RMSE= 0.496 5 。将拟合参数代入式(1),得到卫星运行周期提前时间的拟合函数式,提前时间具有一个周期为3 057.5 d的重复。
3实例分析
某隧道地处天山山脉中段南部、塔里木盆地北缘,附近约3 km 范围内荒无人烟,几乎无植被,仅有少许耐旱、耐盐杂草零星散布。隧址区GPS动态变形监测在隧道的两个洞口外各布设2个监测点,进口端布设GPS1、GPS3点,出口端布设GPS2、GPS4点,GPS3距离洞口较远,GPS3与GPS1、GPS2、GPS4分别相距约200 m、2.3 km、2.4 km。以GPS3作为固定站进行单历元差分解算,短距离基线有利于削弱GPS卫星信号传播路径中的相关性误差。
将2014-09-19和2014-09-20两天的13:50~17:15高频(1 s采样率)观测数据采用GAMIT/GLOBK软件的Track模块进行单历元解算,差分后的坐标残差序列先用db8小波低通滤波去除高频观测噪声[10],之后利用上述的傅里叶拟合曲线估计当日卫星运行周期的提前时间,最后用恒星日滤波法削弱多路径误差[11]。傅里叶拟合曲线估计得到2014-09-20卫星运行周期的提前时间为245.412 s,将当日的坐标残差序列平移245个历元,与19日的坐标残差序列作差,即可用恒星日滤波法削弱当日的多路径误差。由于篇幅原因,本文只对GPS1点坐标残差中的多路径误差削弱情况作出图形分析。由表3可见,N、E、U3个方向的坐标残差均方根值由恒星日滤波前的3.79 mm、3.14 mm、8.80 mm分别缩小到2.82 mm、2.27 mm、6.53 mm,分别缩小25.47%、27.86%、25.80%。图5~7为GPS1点在N、E、U3个方向在恒星日滤波前后的坐标残差对比。恒星日滤波后的坐标残差削弱了多路径影响,坐标残差序列趋向更加平稳、无规律的小幅波动,主要以随机噪声和变形体的变形信息为主。

表3 傅里叶级数恒星日滤波前后坐标残差序列的均方根值统计

图5 恒星日滤波后GPS1点N方向坐标残差Fig.5 N direction residuals before and after sidereal filtering of GPS1 station
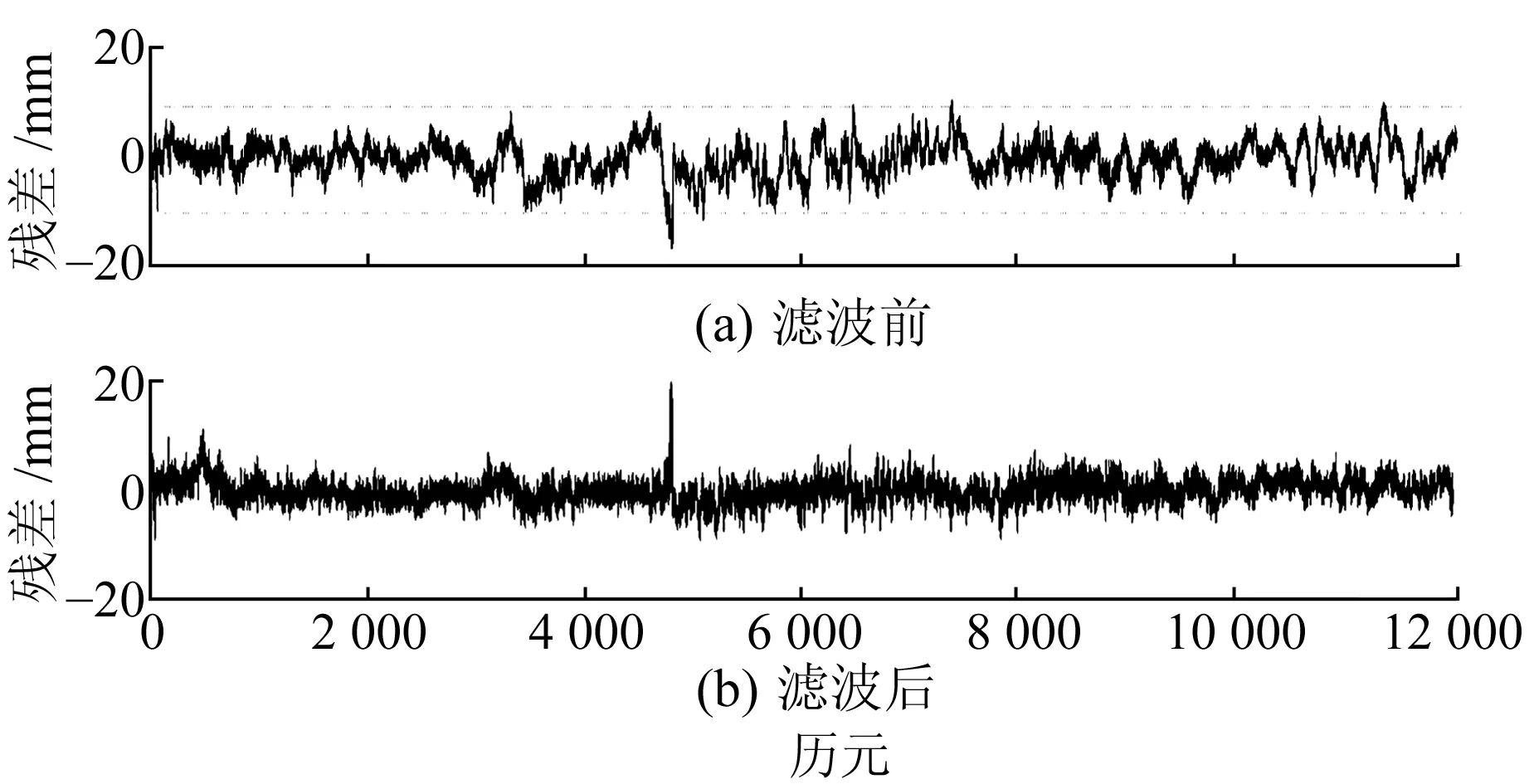
图6 恒星日滤波后GPS1点E方向坐标残差Fig.6 E direction residuals before and after sidereal filtering of GPS1 station

图7 恒星日滤波后GPS1点U方向坐标残差Fig.7 U direction residuals before and after sidereal filtering of GPS1 station
4结语
本文基于三角函数展开形式的傅里叶级数对恒星日滤波方法进行改进,采用超过23 a时长跨度的海量广播星历数据,由广播星历法计算GPS卫星运行周期的每日平均提前时间,将此提前时间作为拟合采样点,用8阶傅里叶三角函数展开式将GPS卫星运行周期的提前时间拟合成关于时间的函数。在实际应用中,只需基于本文提出的拟合函数,通过日期计算卫星运行周期的提前时间,即可免去繁杂的提前时间计算过程,用改进后的恒星日滤波法消除多路径影响。基于三角函数展开式的傅里叶级数的恒星日改进方法,可以缩小点位N、E、U3个方向的坐标残差序列均方根值,消除多路径影响之后的坐标残差序列主要以随机噪声和变形体的变形信息为主。本文提出的基于三角函数展开式的傅里叶级数的恒星日滤波方法,其计算步骤简单并能有效消除多路径影响,有利于提高工程动态变形监测中变形信息的提取能力,可广泛应用于复杂环境下的工程动态变形监测。
参考文献
[1]伊廷华,张永恒,李宏男,等.多路径效应在GPS结构健康监测中的研究进展[J].振动与冲击,2009,28(9):102-108(Yi Tinghua, Zhang Yongheng, Li Hongnan, et al. Study Progress of Multipath Effect in Structural Health Monitoring Based on GPS[J].Journal of Vibration and Shock,2009,28(9):102-108)
[2]黄丁发,陈永奇,丁晓利,等.GPS高层建筑物常荷载振动测试的小波分析[J].振动与冲击,2001,20(1):12-17( Huang Dingfa, Chen Yongqi, Ding Xiaoli, et al. Wavelet-Based Analysis Technique for the Monitoring of Tall Structure under Normal Loading Using GPS[J].Journal of Vibration and Shock,2001,20(1):12-17)
[3]Choi K, Bilich A, Larson K M, et al. Modified Sidereal Filtering: Implications for High-Rate GPS Positioning[J]. Journal of the Korean Orthopaedic Association, 1999, 15(2):178-198
[4]钟萍,袁林果,丁晓利.GPS多路径重复性试验研究[J].测绘科学,2010,35(2):43-45(Zhong Ping, Yuan Linguo, Ding Xiaoli. Experimental Analysis of GPS Multipath Day-to-Day Repeatability[J]. Science of Surveying and Mapping, 2010,35(2):43-45)
[5]Schwahn W, Söhne W. Modified Sidereal Filtering-Tool for the Analysis of High-Rate GPS Coordinate Time Series[J]. International Association of Geodesy Symposia, 2009, 134:219-224
[6]殷海涛,甘卫军,肖根如.恒星日滤波的修正以及对高频GPS定位的影响研究[J].武汉大学学报:信息科学版,2011, 36(5):609-616( Yin Haitao,Gan Weijun,Xiao Genru. Modified Sidereal Filter and Its Effect on High-Rate GPS Positioning[J]. Geomatics and Information Science of Wuhan University,2011, 36(5):609-616)
[7]Larson K M, Bilich A, Axelrad P. Improving the Precision of High-Rate GPS[J]. Journal of Geophysical Research,2007,32(B05 422):1-11
[8]田亮,赵淑芬,赵亚平,等. 基于GPS测站坐标残差序列的傅里叶模型建立与分析[J].测绘技术装备,2012,3(14):11-13(Tian Liang, Zhao Shufen, Zhao Yaping, et al. The Establishment and Analysis of the Fourier Model Based on the GPS Measuring Station Coordinate Residual Series[J]. Geomatics Technology and Equipment,2012,3(14):11-13)
[9]刘维仲,牟景文,戴积成,等.傅里叶级数的曲线仿真应用及算法[J].天津大学学报,1996,29(1):108-112(Liu Weizhong, Mou Jingwen, Dai Jicheng,et al. The Application and Algorithm of Curve Simulation Based on Fourier Series[J]. Journal of Tianjin University, 1996,29(1):108-112)
[10]苏小宁,孟国杰,胡新康,等.高频GPS单历元定位精度及噪声特征[J].大地测量与地球动力学,2014,34(2):150-154(Su Xiaoning, Meng Guojie, Hu Xinkang, et al. Precision and Noise Characteristics of High-Frequency GPS Epoch-by-Epoch Positioning[J]. Journal of Geodesy and Geodynamics,2014,34(2):150-154)
[11]孙常建,杨晓超.GPS多路径效应规律研究[J].测绘通报,2006(11):12-15(Sun Changjian, Yang Xiaochao. The Research of the Rules of GPS Multipath Effect[J]. Bulletin of Surveying and Mapping,2006(11):12-15)
Foundation support:Program for Changjiang Scholars and Innovative Research Team in University,No. IRT13092;State-Province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety;Science and Technology Research and Development Program of China Railway,No.2012G009-C.
About the first author:DUAN Haidong, postgraduate, majors in precise engineering surveying and deformation monitoring,E-mail:466481290@qq.com.
Fourier Series Sidereal Filtering in GPS Dynamic Deformation Analysis
DUANHaidong1,2ZHANGXianzhou1,2MALong1,2LIZulai1,2ZHANGZheng1,2ZHANGZhengguo3LUOYi3
1Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, 999 Xi’an Road, Chengdu 611756, China 2State-Province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety,999 Xi’an Road, Chengdu 611756, China 3High-Speed Railway Track Maintenance Division of Chengdu Railway Bureau,3 Hehuachi Road, Chengdu 610000, China
Abstract:High-rate GPS receivers are popular in real-time dynamic monitoring, but the multi-path effect is one of the key obstacles that restricts its development. However, a sidereal filter can eliminate this effect and improve positioning accuracy. The sidereal filter requires the preset time of each satellite compared to the day before. In this research, 8 526 days broadcast ephemerides are used to calculate the preset time. The Fourier series of 8 orders trigonometric functions is used to fit the series of the preset time. It shows a simple and effective way to estimate the preset time, instead of a more complex calculation. Using this method, the root mean square values of the residual coordinate sequences of N, E and U directions are reduced, and the ability of extracting deformation information is improved.This method therefore can be applied in engineering dynamic deformation monitoring.
Key words:GPS dynamic deformation monitoring; sidereal filtering; method based on broadcast ephemeris; Fourier series; curve fitting
收稿日期:2015-07-25
第一作者简介:段海东,硕士生,主要从事精密工程测量与变形监测研究,E-mail:466481290@qq.com。
DOI:10.14075/j.jgg.2016.07.011
文章编号:1671-5942(2016)07-0609-04
中图分类号:P228
文献标识码:A
项目来源:长江学者和创新团队发展计划( IRT13092);高速铁路运营安全空间信息技术国家地方联合工程实验室项目;原铁道部科技研究开发计划(2012G009-C)。

