用顾及大气层延迟的PVA模型Kalman滤波解算载体运动加速度

王　乐　王跃钢　腾红磊　任强强　黄武星

1　火箭军工程大学304教研室，西安市同心路2号,710025

用顾及大气层延迟的PVA模型Kalman滤波解算载体运动加速度

王乐1王跃钢1腾红磊1任强强1黄武星1

1火箭军工程大学304教研室，西安市同心路2号,710025

摘要：为解算航空重力测量中的载体运动加速度，对GPS载波相位伪距双差观测量进行分析。考虑对流层延迟和电离层延迟的影响，并通过对载体的运动学建模，提出一种基于PVA模型的Kalman滤波算法。相对于传统的差分方法，该算法可从相位观测量中直接解算载体运动加速度。通过仿真分析验证，采用自适应Kalman滤波，得到的未经低通滤波处理的载体加速度标准差为7.26×10-3m/s2。

关键词：GPS双差观测量；运动加速度；对流层延迟；电离层延迟；PVA模型

航空重力测量的基本原理是在重力仪测得的比力中去除载体运动加速度，从而得到重力异常信号[1-2]。因此，载体运动加速度的解算一直是航空重力测量领域的热点问题[3-4]。近20 a来，随着载波相位差分GPS技术的快速发展，载体运动加速度的精度不断提高。目前，利用该技术解算载体运动加速度的差分方法有3种：1)位置微分法[5]，由载波相位导出载体位置，再微分两次得到加速度；2)相位时序差分法[6]，由载波相位微分得到相位率，由相位率导出载体速度，再微分得到加速度；3)加速度直接解法[7]，由载波相位进行两次微分得到相位加速率，再导出载体加速度。研究表明，第3种方法的理论精度最高，但因为采用的是载波相位伪距观测简化模型，忽略了大气层延迟影响，仅适用于短基线测量。张开东[8]分析了简化模型的误差影响，但并未提出有效的改进方法。

近年来，卡尔曼滤波算法在载体运动加速度的解算中得到广泛应用 。应俊俊等[9]采用基于相位的Kalman滤波方法测定载体速度，进而利用非均匀B样条最小二乘拟合方法计算载体加速度。王静波等[10]采用Kalman滤波平滑技术计算航空重力测量中载体速度和加速度。林旭[11]采用基于常加速度模型的ALS-Kalman滤波解算载体加速度，但未考虑大气层延迟。

本文提出一种基于PVA模型(即位置、速度、加速度同时解算的模型)的自适应Kalman滤波算法，能够直接从GPS载波相位双差观测量中同时解算载体的位置、速度和加速度。与传统的差分方法相比，避免了差分过程对噪声的放大作用，并将对流层延迟和电离层延迟的影响包括在状态方程中，计算相应的转移矩阵和协方差矩阵，提高了加速度解算的精度。

1数学方法

1.1观测模型

本文算法的原理是直接从GPS双差载波相位伪距观测量中解算出加速度参数。采用GPS双差相对测量方法可以消除卫星钟差和接收机钟差，削弱电离层延迟和对流层延迟。但在实际测量中，随着载体和基准站相对距离(km级)的增加，差分GPS对大气层延迟的削弱效果将减弱，因此，必须在观测模型中考虑这两种延迟的影响。对于GPS的L1和L2波段载波相位伪距观测量，建立接收机i、j相对于卫星k、l的双差观测模型[12]：

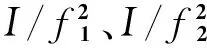
对流层延迟包括天顶干延迟(ZDD)和天顶湿延迟(ZWD)两部分[13]，其中，ZDD可以通过建模精确确定，本文不作讨论；ZWD则需要进行估算。接收机与卫星间的对流层延迟表示为：

(2)

式中，ΔZWD为天顶湿延迟残差，m为映射函数，可采用Saastamoinen模型计算[14]。

1.2载体运动学模型

解算载体运动加速度的Kalman滤波模型表示为:

(3)

式中，Xk为状态向量，Φk为一步转移矩阵，Zk为观测向量，Hk为量测矩阵，Wk、Vk分别是Kalman滤波模型的状态噪声和量测噪声，Qk、Rk分别是状态噪声和量测噪声的协方差阵。

本文旨在利用GPS载波相位伪距双差观测方程，通过建立PVA模型，设计Kalman滤波器，精确解算载体运动加速度，因而需要将对流层延迟和电离层延迟包括到系统状态向量中。另外，观测量中的整周模糊度参数可通过其他算法单独确定，本文不作考虑。因此，系统状态向量表示为：

(4)

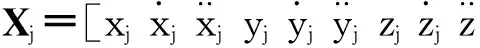
系统状态向量对应的状态转移矩阵表示为:

(5)

由于载体飞行状态较为稳定，对载体进行建模时，采用常加速度模型描述，故载体的状态转移矩阵表示为：

(6)

(7)

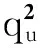
3.2.1推动种植业提质增效 推动长江流域省市加快粮食生产功能区和重要农产品保护区划定，高标准农田建设资金优先支持长江经济带流域第一批完成“两区”划定任务县。支持长江经济带11省(市)建立健全耕地质量监测网络，开展耕地质量调查评价，实施耕地轮作休耕试点。开展绿色高质高效创建，集成全环节绿色高效技术，构建全过程社会化服务体系，打造全链条产业融合模式。支持发展节水农业，培育推广耐旱品种，因地制宜推广管道输水等高效灌溉技术。

双差电离层延迟是关于时间和测量基线长度变化的一阶高斯-马尔科夫过程，可表示为[17]:

(8)

对应的协方差矩阵表示为:

(9)

对流层延迟IΔZWD的协方差矩阵表示为:

(10)

式中，天顶湿延迟谱密度qΔZWD可由经验自协方差函数计算[18]。

1.3量测方程

GPS载波相位双差观测方程是非线性方程，对其作线性化处理，整理为式(3)的形式，其量测矩阵可表示为：

(11)

其中，基准站和载体的坐标组成可表示为：

(12)

对流层天顶湿延迟的系数可表示为：

(13)

量测噪声协方差阵Rk可由量测噪声通过误差传播定律确定[15]。

2仿真验证

由于航空重力测量重点在于解算垂直加速度，本文对所设计的算法进行数值仿真时，重点对垂直方向(即Z方向)的加速度解算进行仿真。由Matlab仿真产生采样频率为1Hz的载波相位伪距测量值的时间序列。为验证本文方法的有效性，分别采用以下2种方案对载体运动加速度进行解算：1)方案1，采用二阶差分法求解加速度；2)方案2，采用本文提出的基于PVA模型的自适应Kalman滤波方法求解加速度。

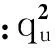
Kalman滤波的过程表示如下：

(14)

表1给出了两种方案的状态估计结果。可以看出，采用二阶差分法计算得到的加速度标准差为2.58×10-2m/s2；本文算法得到的标准差为7.26×10-3m/s2，精度相对较高。究其原因在于：二阶差分法是对GPS位置序列进行差分得到加速度，位置序列的确定本身存在误差，且差分过程放大了噪声，导致最终误差相对偏大；本文算法由于直接对载波相位伪距观测量进行解算，考虑了大气层延迟的影响，并在Kalman滤波过程中对噪声进行了估算，故估计结果较好。

表1　解算精度对比

图1给出了本文所提算法的载体垂直方向加速度解算结果，图2给出了相应的加速度解算精度，精度衡量标准为解算得到的加速度数值相对仿真数据参考值的误差。

需要指出的是，航空重力测量的加速度精度需要达到mGal级，因此，在实际的航空重力测量中，还须对本文的解算结果进行必要的低通滤波处理，在此不作赘述。

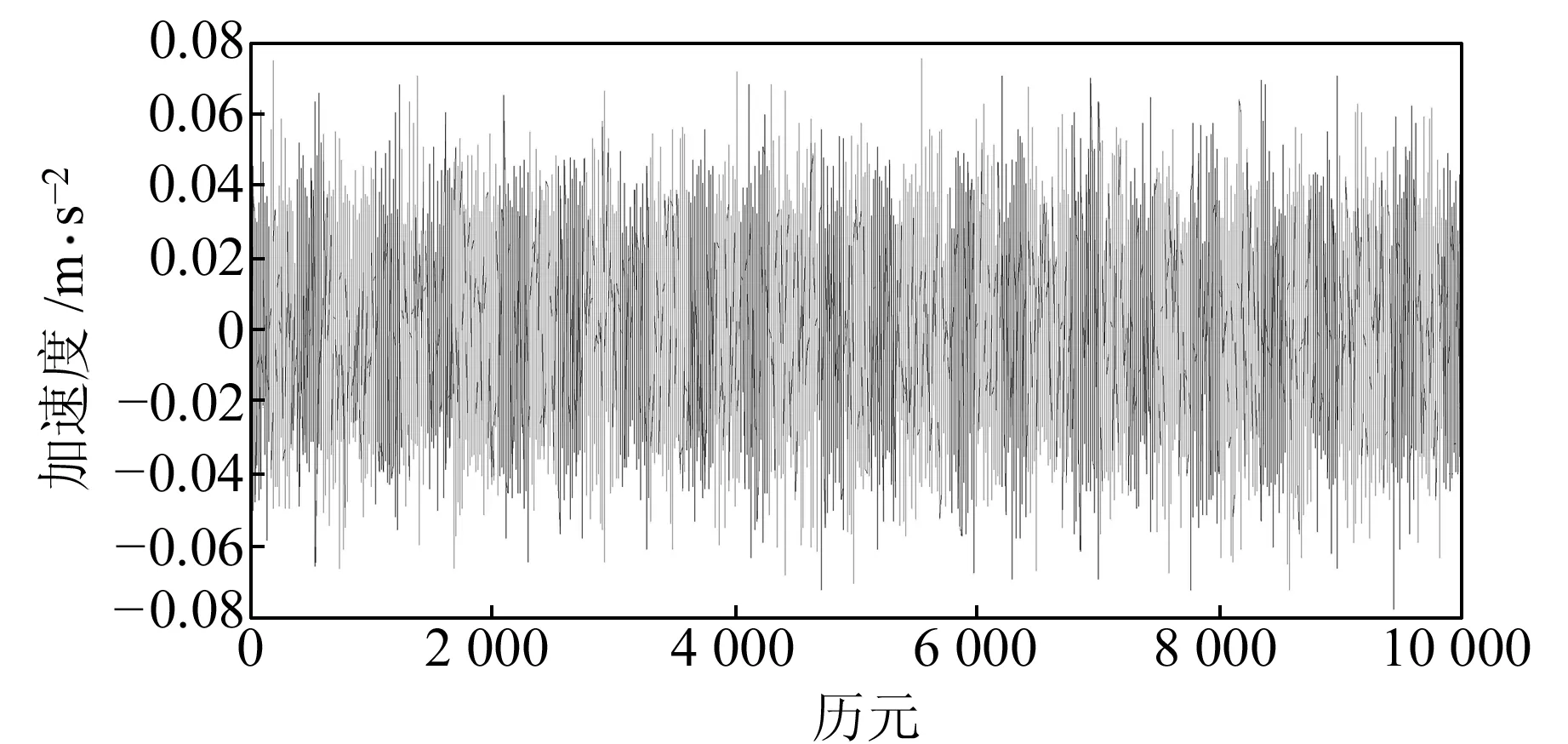
图1　方案2加速度解算结果Fig.1　Results of the estimated accelerations in scheme 2

图2　方案2加速度解算精度Fig.2　Precision of the estimated accelerations in scheme 2

3结语

本文介绍了一种考虑大气层延迟的PVA模型Kalman滤波解算载体运动加速度的方法。该方法直接从GPS载波相位伪距观测值中解算载体运动加速度，考虑了大气层延迟的影响，提高了解算精度。最后通过仿真分析，验证了所提算法的有效性。

然而，关于这种方法还有许多问题值得进一步探讨与研究，如在系统状态转移矩阵中考虑整周模糊度参数的解算，进一步提高算法的实时性和精度等。

参考文献

[1]孙中苗. 航空重力测量理论、方法及应用研究[D]. 郑州：信息工程大学，2004 (Sun Zhongmiao. Theory, Methods and Applieations of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004)

[2]李晓斌. 航空重力测量中GPS定位、速度及加速度解算技术与应用[D]. 北京：中国地质大学(北京)，2010(Li Xiaobin. Determining the Position, Velocity and Acceleration Using GPS in Airborne Gravimetry[D]. Beijing: China University of Geosiciences, 2010)

[3]肖云, 夏哲仁. 航空重力测量中载体运动加速度的确定[J]. 地球物理学报, 2003, 43(1): 62-66 (Xiao Yun, Xia Zheren. Determination of Moving-Base Acceleration in Airborne Gravimetry[J]. Chinese J Geophys,2000, 43(1):62-66)

[4]Jekeli C , Garcia R. GPS Phase Accelerations for Moving-Base Vector Gravimetry[J]. Journal of Geodesy, 1997,71: 630-639

[5]孙中苗, 夏哲仁. FIR低通差分器的设计及其在航空重力测量中的应用[J]. 地球物理学报, 2000, 43(6): 850-855(Sun Zhongmiao, Xia Zheren. Design of FIR Low Pass Differentiator and Its Applications in Air-Borne Gravimetry[J]. Chinese J Geo-Phys，2000, 43(6): 850-855)

[6]Bruton A M, Glennie C L, Schwarz K P. Differentiation for High Precision GPS Velocity and Acceleration Determination[J]. GPS Solutions, 1999, 2(4): 7-21

[7]Jekeli C, Garcia R. GPS Phase Accelerations for Moving-Base Vector Gravimetry[J]. Journal of Geodesy,1997, 71: 630-639

[8]张开东. 基于SINS/DGPS的航空重力测量方法研究[D]. 长沙：国防科学技术大学，2007 (Zhang Kaidong. Research on the Methods of Airborne Gravimetry Based on SINS/DGPS[D]. Changsha: National University of Defense Technology, 2007)

[9]应俊俊，刘根友. 航空重力测量中利用GPS测定载体的速度和垂直加速度[J]. 大地测量与地球动力学, 2009, 29(5): 68-72(Ying Junjun, Liu Genyou. Determination of Velocity and Vertical Acceleration in Airborne Gravimetry by Using GPS[J]. Journal of Geodesy and Geodynamics,2009, 29(5): 68-72)

[10] 王静波，熊盛青，郭志宏，等. 航空重力数据Kalman滤波平滑技术应用研究[J]. 地球物理学进展, 2012, 27(4):1 717-1 722(Wang Jingbo, Xiong Shengqing, Guo Zhihong, et al. Kalman Smoothing for Air-Borne Gravity Data[J]. Progress in Geophys, 2012, 27(4): 1 717-1 722)

[11] 林旭. 自适应Kalman滤波方法及其在航空重力测量中的应用[D]. 武汉：武汉大学，2014 (Lin Xu. Adaptive Kalman Filter and Its Applications in Airborne Vector Gravimetry[D]. Wuhan: Wuhan University, 2014)

[12] Goad C C, Yang M.A New Approach to Precision Airborne GPS Positioning for Photogrammetry[J].Photogrammertic Engineering and Remote Sensing, 1997,63:1 067-1 077

[13] Hofmann-Wellenhof B, Lichtenegger H, Collins J. GPS Theory and Practice(5th ed)[M].Wien, Austria:Springer, 2001

[14]Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J].Geophys Monogr Ser,1972, 15:247-251

[15]Bogatin S, Foppe K, Wasmeier P. Evaluation of Linear Kalman Filter Processing Geodetic Kinematic Measurements[J].Measurement, 2008, 41:561-578

[16]林旭，罗志才，姚朝龙. 常加速度模型的简化自协方差最小二乘法[J]. 测绘学报, 2014, 43(11): 1 144-1 150(Lin Xu, Luo Zhicai, Yao Chaolong. Simplified Autocovariance Least-Squares Method for Constant Acceleration Mode[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1 144-1 150)

[17]Yang M, Tang C H, Yu T T. Development and Assessment of a Medium-Rang Real-Time Kinematic GPS Algorithm Using an Ionospheric Information Filter[J]. Earth Planets Space, 2000, 52: 783-788

[18]Schuler T. On Ground-Based GPS Tropospheric Delay Estimation[D].Munchen:Universität der Bundeswehr,2001

Foundation support:National Defense Pre-Research Foundation of China.

About the first author:WANG Le,postgraduate,majors in GPS precise data processing and algorithm of airborne gravimetry, E-mail: wangaz14@163.com.

Calculation of Motion Acceleration with the Consideration of Atmospheric Delay Using PVA Model Kalman Filter

WANGLe1WANGYuegang1TENGHonglei1RENQingqing1HUANGWuxing1

1304 Unit, Rocket Force University of Engineering, 2 Tongxin Road, Xi’an 710025, China

Abstract:In order to calculate motion acceleration of the airborne gravity measurement, double difference GPS (DDGPS) carrier phase pseudo-range observations are analyzed considering ionospheric and tropospheric delay effects. Then, through the kinematic modeling of the carrier, a new Kalman filtering algorithm based on PVA model is proposed. The algorithm can directly calculate kinematic acceleration from the phase observations, relative to traditional difference method. Validated by the simulation analysis, when adopting the adaptive Kalman filter, the standard deviation of kinematic acceleration without low-pass filtering is 7.26×10-3m/s2.

Key words:GPS double difference observations; kinematic acceleration; tropospheric delay; ionospheric delay; PVA model

收稿日期：2015-11-26

第一作者简介：王乐，硕士生，主要研究方向为航空重力测量中的GPS精密数据处理与算法，E-mail: wangaz14@163.com。

DOI：10.14075/j.jgg.2016.07.020

文章编号：1671-5942(2016)07-0650-04

中图分类号：P223

文献标识码：A

项目来源：国防预研基金。