一种改进的中长基线三频模糊度解算方法研究

刘卫华　吴江飞　栗广才　赵才新　常　岑

1　信息工程大学地理空间信息学院，郑州市科学大道62号,450001

一种改进的中长基线三频模糊度解算方法研究

刘卫华1吴江飞1栗广才1赵才新1常岑1

1信息工程大学地理空间信息学院，郑州市科学大道62号,450001

摘要：研究了一种改进的三频模糊度解算方法。对宽巷和窄巷模糊度固定时受到的噪声误差进行分析得出，选用文中给出的无几何无电离层组合解算的窄巷模糊度噪声标准差均为B3载波波长的8.262 8倍。用实测的北斗三频数据进行了实验验证分析。

关键词：TCAR； 北斗三频； 模糊度解算； 无几何无电离层组合； 噪声标准差

传统的双频模糊度解算方法是以残差平方和最小为准则，通过搜索得到模糊度固定解，该方法比较复杂且计算量大。三频模糊度固定算法简单，能够避免复杂的搜索过程。TCAR(three carrier ambiguity resolution)与CIR(cascade integer resolution)是目前最具代表性的两种三频模糊度解算方法[1-3]，其基本原理均是基于无几何模型的Bootstrapping算法[4]。范建军等[5]指出单历元短基线三频模糊度解算成功率较低的原因主要是TCAR算法中的宽巷模糊度很难确定，并构造了超宽巷和宽巷模糊度的搜索空间，改进了综合TCAR方法。经典TCAR方法由于受到电离层延迟误差的影响，主要适用于短基线的情形[6]。针对中长基线的三频模糊度解算，为了消除电离层延迟项误差对模糊度固定的影响，许多学者提出相应的改进算法[7-9]。对TCAR算法的改进虽然可以消除或减弱电离层延迟误差对模糊度固定的影响，却严重地放大了观测噪声。

本文分析双差电离层残差对TCAR方法中宽巷和窄巷模糊度固定的影响，并深入研究无几何无电离层组合方法求解窄巷模糊度的优缺点。最后，在文中所设定的噪声水平条件下，给出求解相应宽巷和窄巷模糊度的无几何无电离层或无几何弱电离层组合的最优组合系数，并用实测北斗三频数据进行验证。

1影响TCAR算法的因素分析

表1给出了本文所用到的线性组合观测量及其特征值[8]。

表1　BDS三频最优组合观测量及其特征值

本文所选取的超宽巷、宽巷和窄巷组合分别为φ(0,-1,1)、φ(1,-1,0)和φ(0,0,1)，则TCAR的计算过程可表示如下。

1)解算超宽巷模糊度：

(1)

2)解算宽巷模糊度:

(2)

3)解算窄巷模糊度:

(3)

式(1)中解算超宽巷模糊度的组合为一无几何无电离层组合，因此超宽巷模糊度的解算仅受噪声的影响。式(2)和式(3)解算宽巷和窄巷模糊度时，仅消除了几何项误差的影响，所以宽巷和窄巷模糊度的解算除受噪声的影响外，还受到双差电离层延迟误差的影响。

短基线情况下，经典TCAR方法中每一步模糊度浮点解的噪声标准差(单位为周)为：

(4)

(5)

(6)

为不失一般性，假设北斗非差伪距和相位观测值的噪声标准差分别为0.3 m和0.005 m。将相应数值代入式(4)、(5)和(6)，得：

(7)

(8)

(9)

由以上各式可知，以周为单位的超宽巷模糊度浮点解噪声标准差为0.105，因此对于用无几何无电离层组合求解的超宽巷模糊度浮点解直接取整固定，能保证很高的成功率；以周为单位的宽巷和窄巷的模糊度浮点解噪声标准差分别为0.344和0.240，因此在短基线情况下，忽略双差电离层延迟误差后，对宽巷和窄巷模糊度浮点解直接取整固定，也能取得较高的成功率。

在中长基线情况下，不能忽略双差电离层延迟误差的影响，此时宽巷和窄巷模糊度的固定同时受到双差电离层延迟和噪声的影响。假设观测值的噪声误差服从标准正态分布，则TCAR方法中每一步解算得到的模糊度浮点解分别服从下列正态分布[9]：

N(0,-1,1)～N(0，σN(0,-1,1)λ(0,-1,1))

(10)

N(1,-1,0)～N((β(0,-1,1)-β(1,-1,0))δI1,σN(1,-1,0)λ(1,-1,0))

(11)

N(0,0,1)～N((β(1,-1,0)-β(0,0,1))δI1,σN(0,0,1)λ(0,0,1))

(12)

为保证经多历元平滑后得到的宽巷和窄巷模糊度固定解的正确性，应满足下列条件：

(13)

(14)

由式(13)和式(14)分别可得|δI1|<1.420 m和|δI1|<0.042 m。可见，与宽巷模糊度的固定相比，窄巷模糊度的固定对双差电离层延迟误差更为敏感。造成这一结果的原因主要有两个：一是窄巷组合的波长与宽巷组合相比较小；二是在求解宽巷模糊度时，削弱了电离层延迟误差的影响，而求解窄巷模糊度时，放大了电离层延迟误差的影响。实际上，在基线稍长的情况下双差电离层延迟误差很容易超过0.042 m，因此在经典TCAR方法中，对窄巷模糊度浮点解直接取整得到的固定值可靠性不高。图1为一条31.5 km长的基线由正确固定后的模糊度值求得的不同双差卫星对在B1载波上的双差电离层延迟误差。

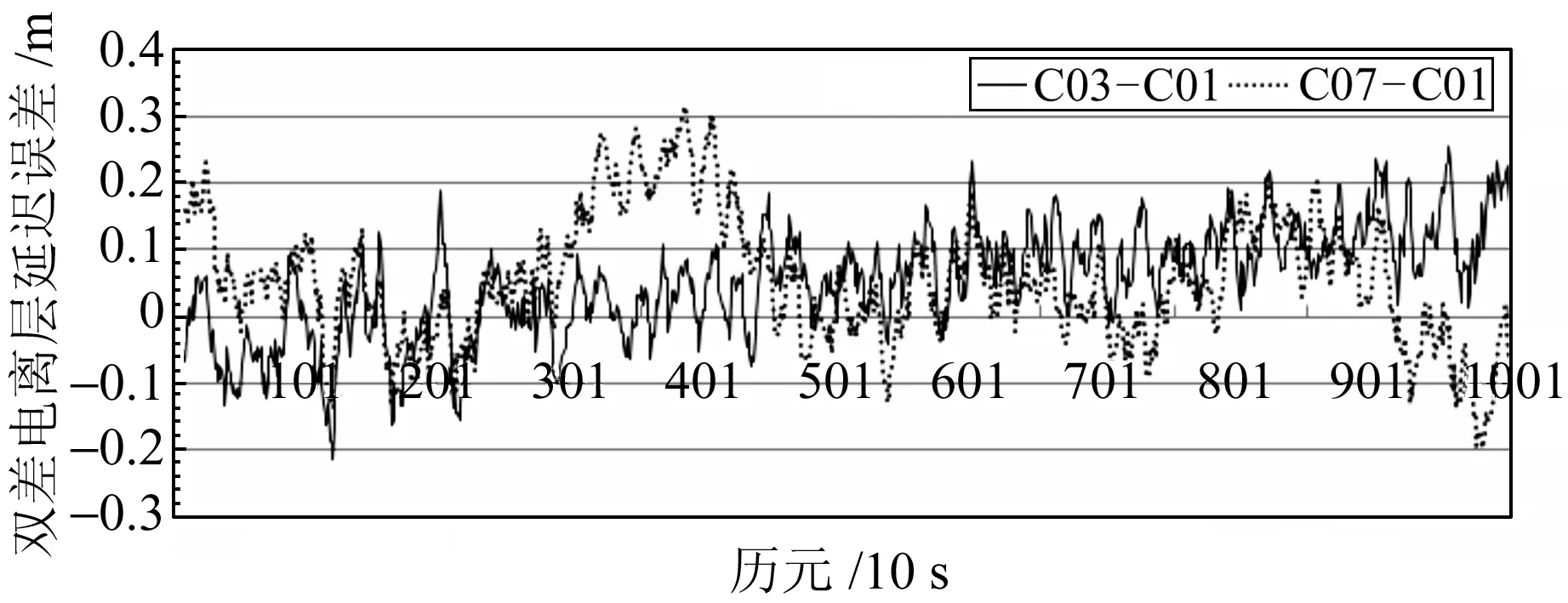
图1　不同差分卫星对的双差电离层延迟误差Fig.1　The DD ionospheric delay error for different differential satellite pairs

由图1可知，对于31.5 km长的基线，两个双差卫星对绝大多数历元的电离层延迟误差均大于0.042 m，但小于1.420 m。因此，对于该中等长度基线而言，宽巷模糊度能高成功率、可靠地固定为整数，而窄巷模糊度的固定成功率则会很低。随着基线长度的增大，双差电离层延迟误差也会相应增大，当双差电离层延迟误差大于1.420 m时，宽巷模糊度的成功率也会随之下降。因此，在中长基线情况下，用TCAR方法进行三频模糊度固定时必须消除或减弱双差电离层延迟误差的影响。

2对TCAR方法的改进

2.1宽巷模糊度的固定

在中长基线情况下，若得到较高的模糊度固定成功率，必须消除或减弱双差电离层延迟误差的影响。参考文献[9]中宽巷模糊度固定的方法，取第一步中模糊度固定的超宽巷组合和3个双差伪距观测值与宽巷组合构成无几何无电离层组合求解宽巷模糊度，其表达式如下：

(15)

其中组合系数a2、b2、c2和d2满足无几何无电离层以及低噪声的条件：

a2+b2+c2+d2=1

(16)

综合电离层延迟与噪声误差对模糊度固定的影响，在电离层延迟误差不太大的情况下，为达到总误差较小的目的，可用弱电离层组合代替无电离层组合：

(17)

上式中,k在0～1的闭区间内取值，可根据不同的双差电离层延迟误差大小调整k的取值，以确保获得最大的宽巷模糊度固定成功率。

表2列出了北斗系统在本文所设置的伪距和相位噪声条件下，用无几何无电离层或无几何弱电离层组合求解宽巷模糊度时的最优组合系数。

表2　不同k值条件下对应的最优组合系数

给定相应的噪声水平和双差电离层延迟，TCAR方法中的宽巷模糊度固定成功率理论上可用以下高斯概率密度函数计算得到：

(18)

式中，x代表模糊度浮点解与正确模糊度值的偏差，μ为模糊度浮点解受到的双差电离层延迟偏差，σ为模糊度浮点解受到的噪声标准差，x、μ和σ均以m为单位。

就北斗系统而言，对于不同的电离层延迟误差，分别用无几何无电离层组合、无几何弱电离层组合和经典TCAR方法，理论上它们对应的宽巷模糊度固定成功率如图2所示。

图2　不同双差电离层延迟水平条件下不同方法对应的单历元宽巷模糊度固定率Fig.2　WL single epoch AR success rate versus DD levels of ionospheric for different methods

由图2可知:1)当双差电离层延迟误差小于0.5m时，用k= 0.2的无几何弱电离层组合单历元求解宽巷模糊度固定的成功率最高；2)当双差电离层延迟误差介于0.5～2.1 m时，用k= 0.1的无几何弱电离层组合单历元求解宽巷模糊度固定的成功率最高；3)当双差电离层延迟误差大于2.1 m时，用无几何无电离层组合单历元求解宽巷模糊度的成功率最高；4)用经典TCAR方法和用k= 0.3的无几何弱电离层组合单历元求解宽巷模糊度的成功率几乎相同。这主要是因为经典TCAR方法与k=0.3的无几何弱电离层组合法的电离层延迟放大系数和噪声标准差均近似相等，由式(18)可知，用这两种方法单历元求解宽巷模糊度的成功率几乎相同。

2.2窄巷模糊度的固定

在三频线性组合中，对于所有的超宽巷和宽巷组合只有两个是独立的，一旦其中的两个被固定，其余的都可以通过简单的线性组合变换得到[10]。因此，可以得到另外的噪声水平较小且模糊度准确固定的三频线性组合观测量。

由于窄巷模糊度的固定对电离层延迟误差比较敏感，所以对于窄巷模糊度的固定使用无几何无电离层组合，以完全消除电离层延迟误差项的影响。参照文献[9]，使用一个模糊度固定的超宽巷组合观测值和一个模糊度固定的宽巷组合观测值，与3个双差伪距观测值以及窄巷组合观测量构成无几何无电离层组合：

(19)

组合系数满足无几何无电离层以及噪声最小条件：

a3+b3+c3+d3+e3=1

(20)

表3列出了几组满足无几何无电离层以及噪声最小条件的组合系数，其中第7列为以m为单位的噪声标准差，第8列为以周为单位的最小噪声标准差相对于B3频点波长的倍数。

表3　最优组合观测量系数及相应的最小噪声水平

从表3可知，3个不同的无几何无电离层组合的噪声水平均较大，因此不能通过单历元获得可靠的窄巷模糊度固定解；选用任一模糊度固定的宽巷观测量组成的无几何无电离层组合的噪声水平都相同，均为B3频点波长的8.262 8倍。

3算例分析

3.1宽巷模糊度固定成功率

使用一条72.6 km的中等长度基线对本文所提出的宽巷模糊度固定方法进行验证。 数据采样间隔为1 s，总历元数为23 528个。统计无几何无电离层组合以及不同k值的无几何弱电离层组合单历元求解宽巷模糊度的固定成功率，并与经典TCAR方法单历元固定宽巷模糊度的成功率进行比较，如表4所示(单位：%)。定义模糊度固定成功率为模糊度正确固定的历元数除以总历元数。

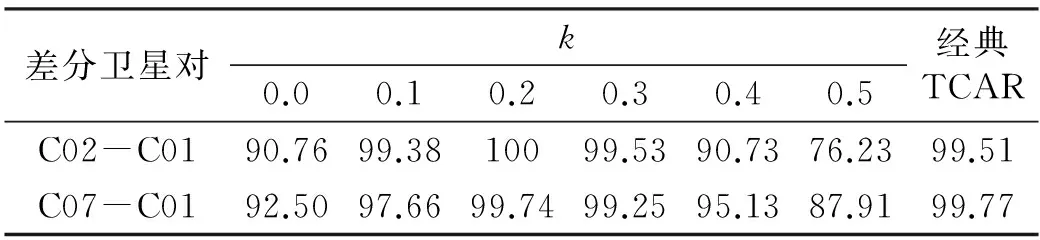
表4　不同k值的改进TCAR方法和经典TCAR方法宽巷模糊度固定成功率

由表4可知，对于双差电离层延迟误差相对较小的中等长度基线，选择k=0.2的弱电离层组合得到的宽巷模糊度固定成功率较其他无电离层或弱电离层组合高，其成功率和经典TCAR方法相当或略高于经典TCAR方法。k=0.3的弱电离层组合得到的宽巷模糊度固定成功率与经典TCAR方法几乎相当，这也验证了由图2得到的第4个结论。

对于长基线，本文使用1组连续观测的北京至上海的北斗实测三频数据(观测时间段内无周跳)，采样时间为2015-02-01，采样间隔为1 s，总历元数为1 800个，基线长度约为1 058.352 km。同样取双差卫星对C02-C01和C07-C01(表5,单位:%)。

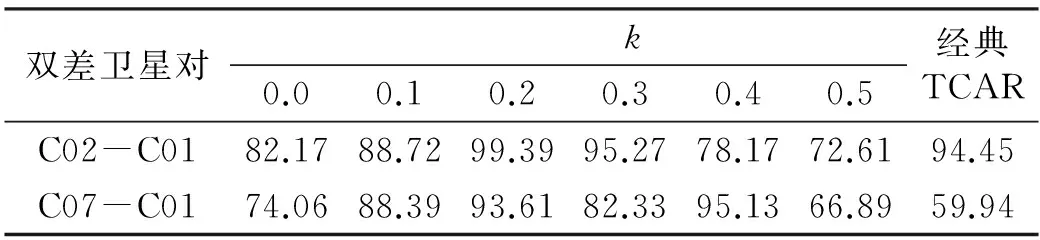
表5　长基线条件下不同k值的改进TCAR方法和经典TCAR方法宽巷模糊度固定成功率

从表5可知，对于该长基线的这两个双差卫星对,用k=0.2的无几何弱电离层组合能得到最大的宽巷模糊度固定成功率。由图2的结论可以推断出，该长基线的双差电离层延迟误差相对较小。表中的无几何无电离层组合求解的宽巷模糊度固定成功率相对较低，这主要是因为消去双差电离层误差的同时放大了噪声的影响。

3.2窄巷模糊度固定

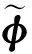
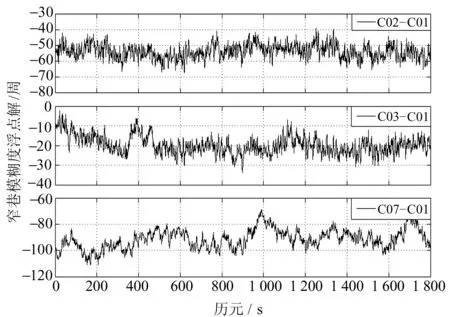
图3　不同双差卫星对的窄巷模糊度浮点解Fig.3　NL float ambiguity resolution of different satellite pairs

从图3可以看出，3个双差卫星对的模糊度浮点解均不能单历元固定模糊度。表3给出了求解窄巷模糊度的无几何无电离层组合的最小噪声标准差，若使噪声标准差通过多历元平滑后减小到B3频点波长的0.5倍，理论上需要的历元个数为275。

图4给出了逐个历元平滑后的窄巷模糊度浮点解,图中从上至下依次为双差卫星对C02-C01、C03-C01和C07-C01平滑后的窄巷模糊度浮点解。由图4可见，经过275个历元平滑后，模糊度依然不能直接取整固定。这主要是因为北斗观测值中的多路径误差的周期较大，无法通过短时间的数据平滑进行消除[11]，因此窄巷模糊度浮点解经275个历元数据平滑后并不能得到正确的模糊度解。因为伪距观测值的多路径误差较大，且双差并不能消除多路径误差，当引进双差伪距观测值组成无几何无电离层组合解算窄巷模糊度时，会使得窄巷模糊度的解算受多路径误差的影响较严重。因此用该无几何无电离层组合解算窄巷模糊度，若不设法消除伪距多路径的影响，会使得窄巷模糊度解算值不可靠。

图4　不同双差卫星对平滑后的窄巷模糊度浮点解Fig.4　Smoothed NL float ambiguity resolution of different satellite pairs

4结语

本文对中长基线条件下影响TCAR的因素进行分析得出，影响宽巷模糊度固定成功率的主要因素是双差电离层延迟，而影响窄巷模糊度固定成功率的主要因素除双差电离层延迟误差外还有噪声误差和多路径误差。在设定的噪声水平条件下，文中给出了用无几何无电离层或无几何弱电离层组合求解宽巷模糊度的最优组合系数。针对窄巷模糊度的固定，选用文中给出的无几何无电离层组合，解算的窄巷模糊度噪声标准差均为B3载波波长的8.262 8倍。最后，通过实测数据简要分析了伪距多路径误差对窄巷模糊度固定的影响。

参考文献

[1]Forssell B, Harris R A, Martinneira M, et al. Carrier Phase Ambiguity Resolution in GNSS-2[C]. ION GPS, Kansas City, 1997[2]Vollath U, Birnbach S, Landau H, et al. Analysis of Three Carrier Ambiguity Resolution(TCAR) Technique for Precise Relative Positioning in GNSS-2[C]. ION GPS,Toulouse, 1998

[3]Hatch R, Jung J, Enge P, et al. Civilian GPS: the Benefits of Three Frequencies[J]. GPS Solution, 2000, 3(4): 1-9

[4]Teunissen P, Joosten P, Christian T, et al. A Comparison of TCAR, CIR and LAMBDA GNSS Ambiguity Resolution[C]. ION GPS, Portland, 2002

[5]范建军，王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报，2007，36(1):43-49.(Fan Jianjun, Wang Feixue. A Method for GNSS Three Frequency Ambiguity Resolution Based on Short Baselines[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 43-49)

[6]李金龙. 北斗/GPS多频实时精密定位理论与算法[D]. 郑州： 信息工程大学，2014 (Li Jinlong. BDS/GPS Multi-Frequency Real-Time Kinematic Positioning Theory and Algorithms[D]. Zhengzhou: Information Engineering University, 2014)

[7]Feng Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862

[8]Tang W M, Deng C L, Shi C,et al. Triple-Frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J]. GPS Solution, 2013, 18(3): 335-344

[9]Zhao Q L, Dai Z Q, Hu Z G, et al. Three-Carrier Ambiguity Resolution Using the Modified TCAR Method[J]. GPS Solution, 2014, 19(4): 589-599

[10] LI B F, Feng Y M, Shen Y Z. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-Generated Triple Frequency GPS Signals[J]. GPS Solution, 2010, 14(2): 177-184

[11] Zhang X H, He X Y. Performance Analysis of Triple-Frequency Ambiguity Resolution with Beidou Observations[J]. GPS Solution, 2016, 20(2): 269-281

Foundation support:National Natural Science Foundation of China, No.41174006; China Postdoctoral Science Foundation, No.201003772,20100481458.About the first author:LIU Weihua，postgraduate，majors in GNSS data processing, E-mail: 1113988385@qq.com.

Study of a Modified Method for Medium and Long Triple-Frequency Ambiguity Resolution

LIUWeihua1WUJiangfei1LIGuangcai1ZHAOCaixin1CHANGCen1

1Institute of Surveying and Mapping，Information Engineering University，62 Kexue Road, Zhengzhou 450001，China

Abstract:This paper studies a modified TCAR method and analyzes the noise error that affects the ambiguity resolution of wide-lane(WL) and NL, and points out that the noise standard deviation of the geometry-free and ionosphere-free combinations given by this paper all equal 8.262 8 times the B3 carrierwave length. Finally, the real measured Beidou navigation satellite system(BDS) triple-frequency data is used to verify and analyze the conclusion.

Key words:TCAR; BDS triple-frequency; ambiguity resolution; geometry-free and ionosphere-free combination; noise standard deviation

收稿日期：2015-11-10

第一作者简介：刘卫华，硕士生，研究方向为GNSS数据处理，E-mail: 1113988385@qq.com。

DOI：10.14075/j.jgg.2016.07.005

文章编号：1671-5942(2016)07-0581-05

中图分类号：P228

文献标识码：A

项目来源：国家自然科学基金(41174006)；中国博士后科学基金(201003772,20100481458)。