LMD-GM(1,1)模型及其在变形监测中的应用
池其才 周世健 王奉伟
1 东华理工大学测绘工程学院,南昌市广兰大道418号,330013 2 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013 3 南昌航空大学校长办公室,南昌市丰和南大道696号,330063
LMD-GM(1,1)模型及其在变形监测中的应用
池其才1,2周世健3王奉伟1,2
1东华理工大学测绘工程学院,南昌市广兰大道418号,330013 2流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013 3南昌航空大学校长办公室,南昌市丰和南大道696号,330063
摘要:将局部均值分解(LMD)方法应用在监测数据中。实验结果表明,LMD-GM(1,1)模型的拟合效果和预测效果比EMD-GM(1,1)模型和GM(1,1)模型好,具有更高的应用价值。
关键词:局部均值分解(LMD); GM(1,1)模型; 经验模态分解(EMD); LMD-GM(1,1)模型
常用的变形量预测方法有时间序列法、人工神经网络、灰色理论和模糊方法等[1-4]。大坝水平位移是非平稳序列,而传统的预测方法假设其为平稳序列,预测精度往往不高。为了提高精度,将数据进行分解,常用的方法有小波分解和经验模态分解(EMD)[5-6]。前者不是自适应性的,精度很难控制;后者虽然是自适应性的,但其IMF分量必须满足一个条件,即在整个数据段内,极值点的个数和过零点的个数必须相等或者相差最多不超过1个,这就限制了在IMF分量的任意两个相邻极值点之间不可能存在非过零点的局部波动。与此相反,局部均值分解(local mean decomposition,LMD)方法中,PF分量定义为一个纯调频信号和相应的时变包络信号的乘积。所以在实际信号分析中,PF分量相比于IMF分量可以反映更多的原信号局部特征信息。本文将LMD模型和GM(1,1)模型相结合,对大坝位移进行短期预测,并将拟合结果和预测结果与其他模型进行比较分析。结果表明,本文模型在多尺度变形监测中具有更好的实用性。
1LMD基本算法
LMD方法不仅可以自适应地对任一信号进行分解,且得到的分解量具有非负性和物理意义。获取PF单分量值后,再求解其瞬时幅值及频率。包络信号可认为是单分量值的瞬时幅值,并且单分量值的瞬时频率是在纯调频信号的基础上通过直接法解算出的。最后通过单分量值中瞬时频率及幅值不断分类合并,从而获取时频分布图。对一任意信号x(t),其分解过程如下[7]。
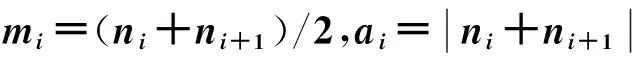
2)把局部均值函数m11(t)不断从仿真信号x(t)中分离出来,得到h11(t)=x(t)-m11(t),解调h11(t),得到x11(t)=h11(t)/a11(t)。理论上,s11(t)为纯调频信息量,a12(t)=1为其局部包络函数。如果a12(t)≠1,那么重复以上程序,直至s1n(t)为纯调频信息值,也就符合s1n(t)的包络估计函数a1(n+1)(t)=1。

4)获取仿真信号中的首个PF1单分量值后,把包络信号a1(t)与纯调频信号s1n(t)相乘,可获取PF1(t)=a1(t)s1n(t)。
5)将PF1值从仿真信号x(t)中除去,获取新的信号量:
(1)
把u1(t)理解为仿真数据,按上述步骤不断运算k次,直至uk(t)为一个一次函数为止。依据以上得出的各个分量值,仿真信号可被k个单分量PF及uk(t)重新组合构成,即
(2)
2传统GM(1,1)预测模型建模机理[8]

GM(1,1)模型的白化型响应式为:
由最小二乘法得:
其中,
3LMD-GM(1,1)模型
灰色GM(1,1)模型只对短期数据具有较强的适应能力,且要求数据最好具有单调性。由于大坝监测数据序列的影响因素复杂,是非平稳数据,直接利用灰色GM(1,1)模型进行拟合和预测,其精度往往不高。本文采用LMD方法先对数据进行分解,得到PF分量和余项res,并绘制出各个分量的曲线图,观察其规律性,采用适宜的方法进行拟合与预测。余项res具有单调性,可直接采用GM(1,1)模型进行拟合与预测,最终将这些结果叠加。
4实例分析
对四川省广元市三维镇境内的宝珠寺水电站大坝22号坝段551 m高程的3号测点水平位移分别建立GM(1,1)灰色模型、EMD-GM(1,1)模型和LMD-GM(1,1)模型。表1为测点2004~2009年之间的一组监测数据[9],用这3种模型分别拟合此数据并计算出预测值,通过计算残差值来检验模型精度。

表1 大坝位移量的实测数据
利用LMD模型对大坝的位移量进行分解,得到PF1、PF2和余项res(表2),并画出分解结果的曲线图(图1)。从图1可以看出,分量PF1具有较强的周期性,故采用周期函数进行预测;分量PF2采用SVM(支持向量机)进行预测;余量res具有单调性,采用GM(1,1)进行预测。PF1、PF2和余量res的拟合结果见表3。
由表3和表4分别计算各模型拟合值和预测值的残差平方和的平均数MSE。可以看出,LMD-GM(1,1)模型的拟合值和预测值的MSE都明显小于EMD-GM(1,1)模型和GM(1,1)模型。各模型拟合值与实测值的曲线图见图2。

表2 LMD分解得到的PF1、PF2和余项res

图1 PF1、PF2和余项res的曲线图Fig.1 The curves of PF1,PF2 and res

时间实测/mmGM(1,1)模型EMD-GM(1,1)模型LMD-GM(1,1)模型拟合值/mm残差/mm拟合值/mm残差/mm拟合值/mm残差/mm2004-120.450.45000.00000.4635-0.01350.01910.43092005-06-2.83-2.6598-0.1702-2.4760-0.3540-3.08910.25912005-12-0.31-0.1535-0.1565-0.2200-0.0900-0.39800.08802006-06-3.98-3.7416-0.2384-3.8470-0.1330-3.5368-0.44322006-12-0.61-0.3285-0.2815-0.67200.0620-0.6129-0.00292007-06-3.38-2.9753-0.4047-3.52300.1430-3.3921-0.01212007-12-0.98-0.5639-0.4161-1.03600.0560-0.9062-0.07382008-06-4.38-4.67510.2951-4.3630-0.0170-4.15910.2209MSE0.30680.08950.0639

表4 各方法预测值与实测值对比
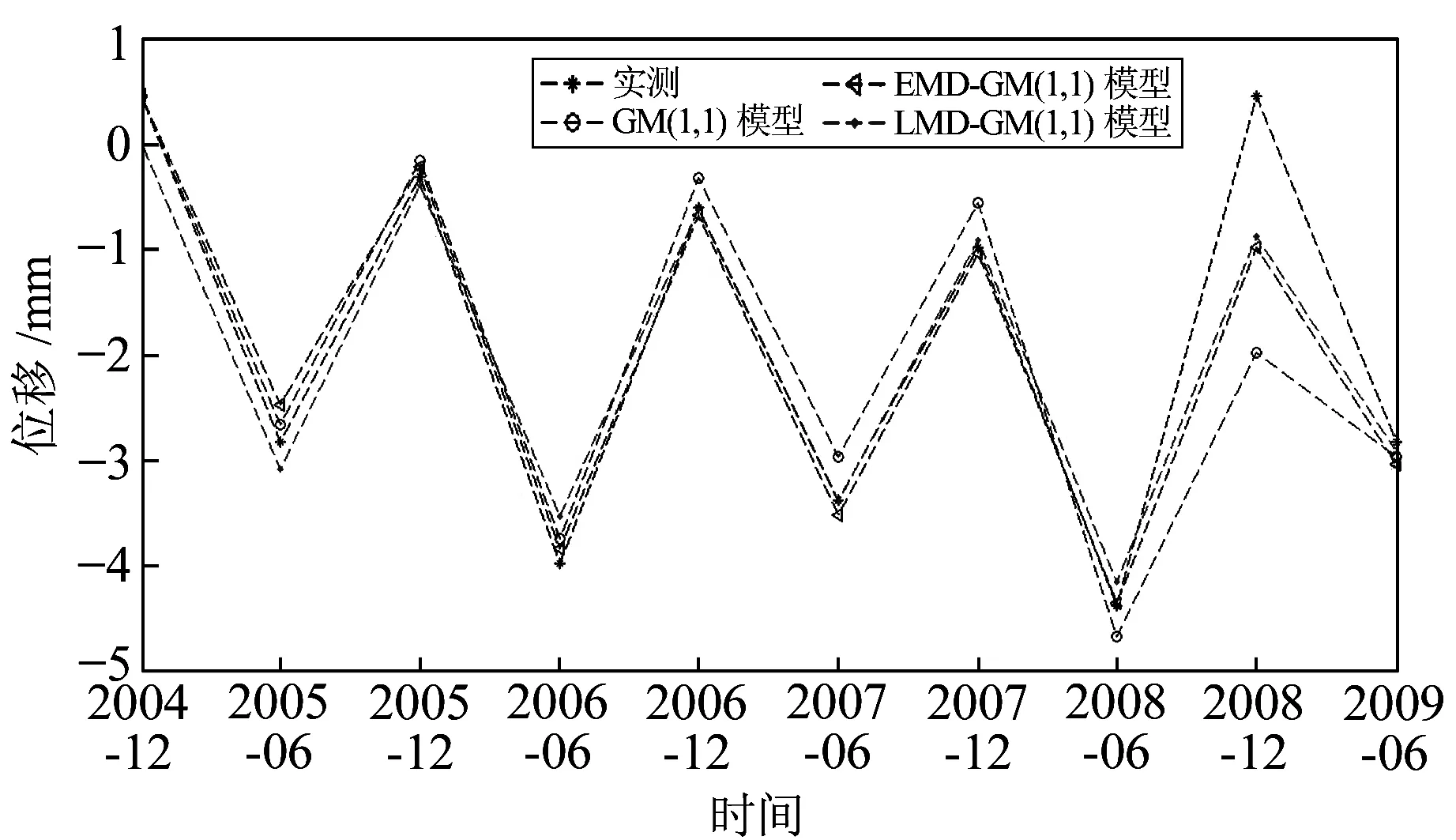
图2 各个模型拟合值的曲线图Fig.2 Fitted values curve of each model
5结语
本文通过LMD把大坝水平位移数据序列分解成独立的PF分量和余项res,采用适宜的模型对PF分量进行建模,采用GM(1,1)模型对余项res进行建模,最后将这些结果进行叠加,得到最终的预测结果。从实验结果可以看出,LMD-GM(1,1)模型的拟合精度和预测精度相对于其他两种模型都有很大提高。
参考文献
[1]李捷斌, 孔令杰. 基于Kalman滤波的BP神经网络方法在大坝变形预测中的应用[J]. 大地测量与地球动力学, 2009, 29(4):124-126 (Li Jiebin,Kong Lingjie. Applicationg of BP Neural Network Based on Kalman Filtering to Dam Deformation Prediction[J]. Journal of Geodsey and Geodynamics,2009, 29(4):124-126)
[2]池其才, 周世健, 王奉伟. 基于时间序列的变形监测数据处理方法比较研究[J]. 测绘与空间地理信息, 2015(7):193-195 (Chi Qicai,Zhou Shijian,Wang Fengwei. Deformation Monitor Data Processing Methods Based on Time Series Comparative[J]. Geomatics & Spatial Information Technology, 2015(7):193-195)
[3]国计鑫. 小波分析与时间序列组合模型在变形监测分析预测中的应用研究[D]. 西安:长安大学, 2014 (Guo Jixin. Application of Wavelet Analysis and Time Series Analysis Combined Model in Predicting the Deformation Monitoring[D]. Xi’an: Chang’an University,2014)
[4]蓝悦明, 王新洲. 灰色预测用于大坝水平变形预测的研究[J]. 武汉测绘科技大学学报, 1996(4):350-354 (Lan Yueming, Wang Xinzhou. Research of Grey Forecast on Dam Level Displacement[J].Journal of Wuhan Technical University of Surveying and Mapping,1996(4):350-354)
[5]罗飞雪, 戴吾蛟. 小波分解与EMD在变形监测应用中的比较[J]. 大地测量与地球动力学, 2010, 30(3):137-141 (Luo Feixue, Dai Wujiao. Comparison of EMD with Wavelet Decomposition for Dynamic Deformation Monitoring[D].Journal of Geodsey and Geodynamics,2010, 30(3):137-141)
[6]范千, 方绪华. 基于经验模式分解消噪的高层建筑物变形监测数据处理方法[J]. 江南大学学报:自然科学版, 2010, 9(5):555-558 (Fan Qian, Fang Xuhua. Method of Deformation Monitoring Data Processing for High-Rise Building Based on Empirical Mode Decomposition Denoising[J].Journal of Jiangnan University:Natural Science Edition, 2010, 9(5):555-558)
[7]Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface, 2012, 11(3):703-704
[8]邓聚龙. 灰理论基础[M].武汉:华中科技大学出版社,2002(Deng Julong.Outline on Grey System Theory[M].Wuhan: Huazhong University of Science and Technology Press, 2002)
[9]蔡小辉, 张瀚, 崔冬冬. EMD-GM(1,1)模型及在大坝变形预测中的应用[J]. 人民长江, 2011, 42(10):91-94 (Cai Xiaohui,Zhang Han,Cui Dongdong.Research on EMD-GM(1,1) Model and Its Application in Dam Displacement Forecast[J]. Yangtze River,2011, 42(10):91-94)
Foundation support:National Natural Science Foundation of China, No.41374007; Innovation Fund Designated for Graduate Students of Jiangxi Province, No.YC2015-S262; Fund of Educational Innovation for Graduate Students of Jiangxi Province (Surveying,Mapping and Geoinformation).
About the first author:CHI Qicai, postgraduate, majors in deformation monitoring, E-mail:chiqicai126.com.
LMD-GM(1,1) Model and Its Application in Deformation Forecating
CHIQicai1,2ZHOUShijian3WANGFengwei1,2
1Faculty of Geomatics, East China University of Technology,418 Guanglan Road,Nanchang 330013, China 2Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road,Nanchang 330013, China 3Principal’s Office,Nanchang Hangkong University, 696 Fenghenan Road, Nanchang 330063,China
Abstract:Local mean decomposition (LMD) method is applied in monitoring data. Experimental data show that the fitting effect of the LMD-GM (1, 1) model is better than those of the EMD-GM (1,1) and GM (1,1) models. Therefore, LMD-GM (1,1) model has a higher application value in deformation monitoring.
Key words:local mean decomposition (LMD);GM(1,1);empirical mode decomposition (EMD); LMD-GM(1,1)
收稿日期:2015-11-24
第一作者简介:池其才,硕士生,主要研究方向为变形监测,E-mail:chiqicai126.com。 通讯作者:周世健,博士,教授,博士生导师,主要研究方向为变形监测、GIS质量评价等,E-mail:408608628@qq.com。
DOI:10.14075/j.jgg.2016.07.012
文章编号:1671-5942(2016)07-0613-04
中图分类号:P258
文献标识码:A
Corresponding author:ZHOU Shijian,PhD, professor,PhD supervisor,majors in deformation monitoring and GIS quality evaluation, E-mail:408608628@qq.com.
项目来源:国家自然科学基金(41374007);江西省研究生创新基金(YC2015-S262);测绘地理信息江西省研究生创新教育基地项目。

