基于最小二乘法的改进的Logistic人口模型
李苑等

【摘 要】人口变化对社会发展有着直接的影响。人口增长率是研究人口增长的重要指标之一,人口增长的预测对人口政策的制定有着非常重要的作用。本文在有关人口的理论知识基础上,根据中国1971年-2014年人口数据,基于最小二乘法的改进的Logistic模型,分别建立模型来预测中国人口的增长趋势,并将预测的函数曲线与真实数据进行比较,得到较好的结果。利用曲线拟合的理论,采用MATLAB软件得到阻滞函数,再用Logistic模型来预测中国人口。结合我国人口低出生率、人口老龄化等问题,国家调整决定开放二胎政策,以期将我国人口调整为更加合理的发展方向。
【关键词】人口增长; Logistic模型;曲线拟合
【Abstract】Population change of future social development has a direct impact. The population growth rate is an important indicator of research and population growth, population growth has a very important role in the formulation of population policies. In this paper, based on the theoretical knowledge of the relevant population, according to the 1971 to 2014 population data, Chinese population Logistic model based on the theory of differential equations, respectively model to predict the growth trend of China's population. And predictable function curve and real data to get better results. Using the theory of curve fitting using the MATLAB software block function, and then the Logistic model predicted that China's population.Combined with the problem of the low birth rate and aging population,China decide to adjust the policy of opening a second child to make our country become better.
【Keywords】Population growth;Logistic model;Curve fitting
0 引言
人口总数的预测是人口研究中最重要、最基本的内容之一,未来人口总数不仅对自身有重要意义,同时也是其他预测的基础。人口预测的基本方法是在认识人口发展变化的客观规律和人口变量的特征及其内在联系的基础上,建立数学模型来进行测算。研究人口问题不仅需要对人口总数进行研究,还要对人口总数的总体状况、变化趋势、发展规模以及对影响人口发展的各种因素等进行研究。本文将以往的人口预测模型进行改进并结合最小二乘法,拟合出较为符合实际的人口变化情况。以往的人口预测对于增长率的研究不是十分理想,对于人口阻滞增长模型的各种因素对人口增长的影响程度没有具体的量化,只是以一种定性研究存在。本文通过改进Logistic 模型中的增长率计算方式使得于预测更加准确。通过查阅中国统计年鉴了解我国从1970年到2014的人口总数,利用以往的Logistic模型进行计算,并画图拟合出中国人口变化情况。将以往Logistic模型中的参数进行改进,利用改进后的Logistic模型进行计算,同时计算出人口增长率,作图拟合出增长率的变化情况,不难发现改进后的模型计算所得结果相比于原来的模型更加符合实际情况。利用结合最小二乘法的改进Logistic模型进行人口总数的预测有较好的结果。人口的变动会影响到基本国策的制定,联系当今中国国情和开放二胎政策,使得对人口总量以及增长率的研究变得尤为重要。目前我国人口低出生率、老龄化状况明显,这种现象对于我国的年龄组成是一种巨大的挑战,为使我国人口可以以一种健康稳定的态势发展,中国政府结合实际情况正开展逐步放开生二胎的政策,以期可以顺利调整人口状况,使我国以更加合理的方式发展。
1 相关理论
1.1 人口阻滞增长模型(Logistic 模型)
2 人口预测模型建立
2.1 中国总人口的估计Logistic模型
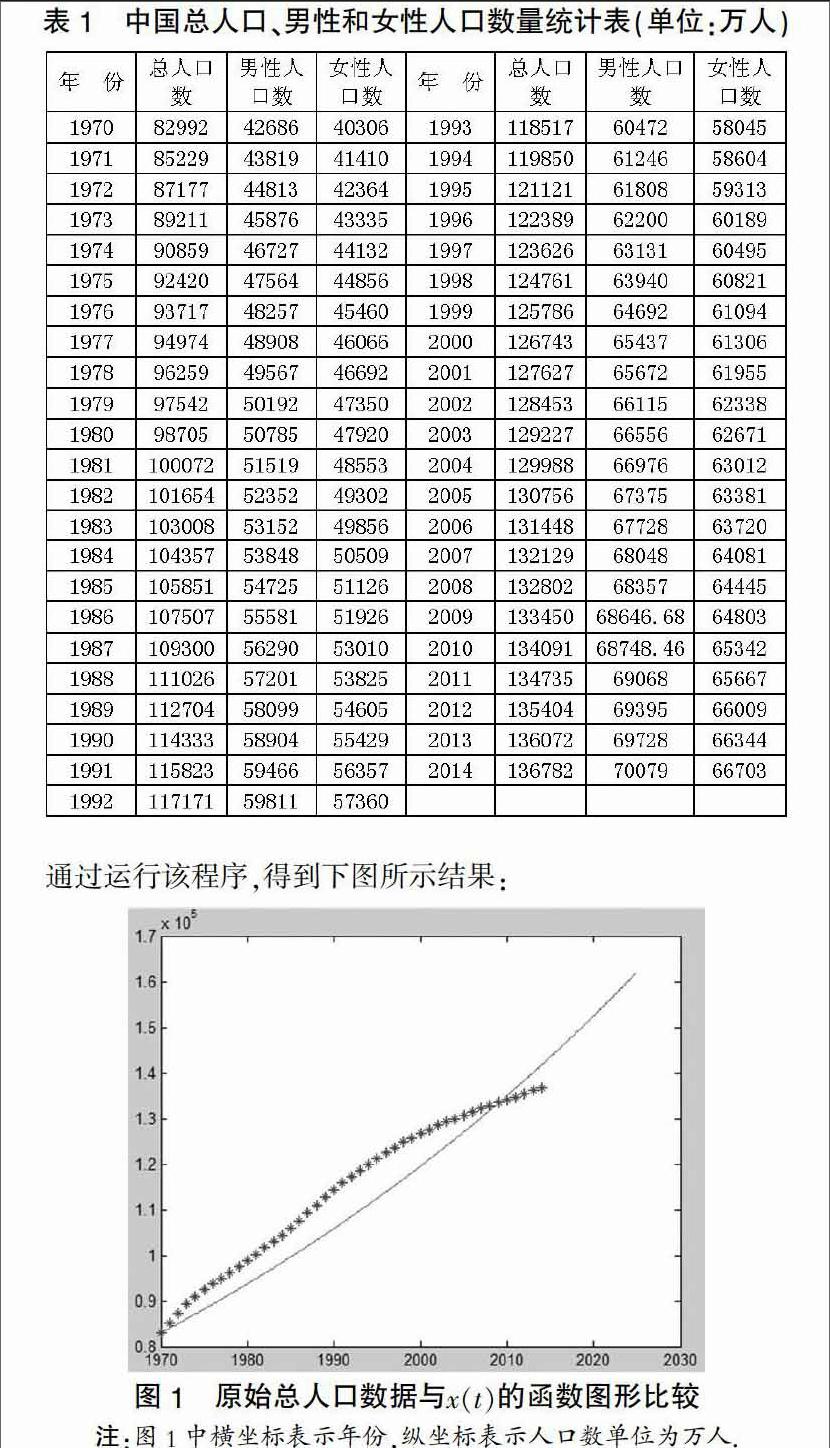
通过查阅2014年中国统计年鉴,得到从1970年到2014年中国总人口、男性和女性人口数量表格。由于表1.1从1949年到1969年之间数据不全,我们选取从1970年到2014年的数据进行分析处理,先计算出这40年间各类人口的平均增长率,总人口平均增长率分别为0.01216032,设X(t)=x(t),其中x(t)表示第t年总人口的数量,并以1970年的人口数据X0=x0作为t=0年的数据,将这些数据公式代入(1.1),得到x(t)=82992e0.01216032t(1.5)。
为了验证预测结过的合理性,我们将1970到2014年的原始总人口数据与利用公式(1.5)中x(t)的函数图形进行比较,利用MATLAB编写程序[7]如下:
2.2 改进的Logistic 模型
在Logistic模型中,对公式(1.4)系数r、xm主要通过估计[9]或统计得到,来分析预测人口发展态势。事实上我们知道r(x)为x的线性减函数,即r(x)=r-sx,(r>0,s>0),而系数r、s不好确定。为此我们改进Logistic模型中r(x)确定方法,我们根据人口的每年的变化率与人口数量之间的关系,采用曲线拟合的方式来确定r(x)=r-sx的参数r、s,对具体人口预测效果会更好。
2.2.1 中国人口增长率的拟合
我们通过利用表1.的数据可以计算出从1970-2014年的中国人口的增长率
2.2.2 中国人口阻滞增长函数的拟合
为了得到Logistic模型的阻滞增长函数r(x)=r-sx,(r>0,s>0),的系数我们利用最小二乘拟合方法来拟合增长率r(x)与人口总数x之间的函数关系。根据表2编写MATLAB程序,来拟合增长率与人口总数之间的关系。
运行可得到中国人口阻滞增长函数r(x)=0.0678-0.0047x。同时得到中国人口增长率与人口数量(亿)的关系和拟合的阻滞增长函数对比关系。
2.2.3 应用改进的Logistic 模型方法预测中国人口
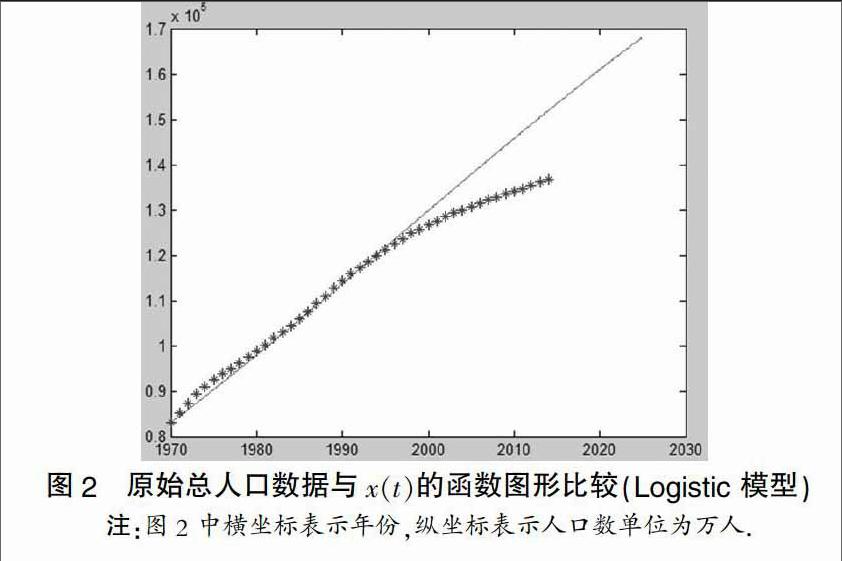
为了验证预测结过的合理性,我们将1970到2014年的原始总人口数据与利用公式(1.7)中x(t)的函数图形进行比较,利用MATLAB编写程序如下:
通过分析利用Logistic 模型求出的总人口数据与x(t)的函数图形比较,利用改进的Logistic 模型求出的总人口数据与x(t)的函数图形比较可以发现图4更准确,更具有实际意义[10]。
3 结束语
人口增长系统是一个复杂的动态系统,人口变化对未来经济,社会发展有着直接的影响。人口增长率是研究人口增长的重要指标之一,人口增长的预测对人口政策的制定有着非常重要的作用。我国人口总数在逐年增加,人口质量明显提高,但增长率却是降低的。通过人口数据的处理和图像拟合的结果不难看出这一规律。人口的增长变化主要是由自身的发展规律和客观条件决定的。对于我国现状而言,由于出生率低,国家人口规划指出要完善生育政策在低出生率和人口老龄化加速的社会大趋势下,在计划生育基本国策不变的前提下做出一定程度的变化,国家决定“开放二胎”政策。全国分步实施以期达到全国全面放开二胎的目标。进一步改善我国人口低出生率和老龄化的现状,提高我国的人口净增长率。
【参考文献】
[1]郑小洋,罗其莉,姚蕾,宋江敏.人口阻滞增长模型的参数估计与程序实现[J].数学学习与研究,2015,01:132.
[2]余惠霖.几种常微分方程解法中的数学化归思想[J].柳州师专学报,2011,02:123-126.
[3]沈小凤.几类人口预测模型的改进及实证分析[D].中央民族大学,2012.
[4]余爱华.Logistic模型的研究[D].南京林业大学,2003.
[5]贾小勇,徐传胜,白欣.最小二乘法的创立及其思想方法[J].西北大学学报:自然科学版,2006,03:507-511.
[6]程玉民.移动最小二乘法研究进展与述评[J].计算机辅助工程,2009,02:5-11+20.
[7]姜衍猛.基于MATLAB的数据采集与分析系统的研究及设计[D].山东大学,2012.
[8]杨莉.人口预测中的数学模型探析[J].中国电力教育,2006,S4:106-108.
[9]葛华才,樊晓贺.实验数据线性拟合时应注意的问题[J].实验室科学,2010,06:91-93.
[10]王彦,马伯强,20世纪80年代以来我国人口发展的数学模型和展望[J],北京大学学报:自然科学版,39(增刊):28-33,2003.
[责任编辑:曹明明]

