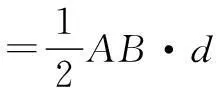拓展思维空间 激发创新意识

朱春强

(江苏省宜兴市第二高级中学，214204)



拓展思维空间激发创新意识

朱春强

(江苏省宜兴市第二高级中学，214204)

创新是时代的要求,创新教育势在必行.中学的创新教育,主要定位于培养学生的创新意识.在中学数学教学中,就是着力去开发学生的思维空间,让学生在数学学习中自主探究,发现问题,解决问题,有所创造．运用多媒体辅助教学，利用《几何画板》软件在解析几何教学中的强大功能(能够动态地保持给定的几何关系),可形象、生动、直观地让学生感受数学,从而培养和拓展学生的思维空间,激发学生的创新意识．

前不久，笔者利用多媒体辅助教学,在校内开设了一堂公开课.这里谈一下笔者对“直线与圆关系”一课的教学认识,也算是对创新教育教学模式的一次尝试．

一、教学目标

(1)认知目标:探讨、判断直线与圆位置关系的方法;熟悉掌握、运用圆中半弦、弦心距、半径之间的关系．

(2)能力目标:提高猜想,合理推理能力．培养发现问题、提出问题,并用所学的数学知识解决问题的能力．

(3)情感目标:通过对问题的探究,利用多媒体的优越性,直观、动态地感受,研究几何图形,感悟数学美．

二、教学重点、难点

强化发现问题、认识问题的意识,感受、认识、理解几何图形的位置关系,通过直观发现,感受数学的内在美．

三、教学方法

利用多媒体辅助教学手段，充分发挥几何画板在解析几何教学中的强大功能及Powerpoint动画设计功能.

四、教学过程

1.复习

(1)判断直线与圆位置关系的方法:

(i)圆心到直线的距离d与圆半径r的关系；

(ii)直线与圆的方程联立,通过判别式Δ(相离:d>r⟺ Δ< 0,相切:d=r⟺Δ=0, 相交d0).

(2)圆中半弦m,弦心距d,半径r之间的关系:m2+d2=r2.

(学生在初中对以上问题较熟悉,结论易得)

2.通过一题多变训练学生思维的变通性

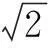
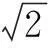
设计变题

(1)距离为1的点有几个?

(2)距离为2的点有几个?

(4)距离为5的点有几个?

(用同样的分析方法,直观发现答案分别为4,2,1,0个)

通过例1,让学生直观感受几何图形,总结结论(学生总结).

点的个数与直线l垂直的圆的直径两端点到直线l的距离有关．

设计意图改变题设中的距离数值,发现问题规律．利用PowerPoint动画设计功能,直观、明显地得出结论.学生通过观察,可以很快得到结论,培养学生发现问题的能力.

例2已知圆x2+y2=1,当k为何值时，直线l：y=k(x-2)+3与圆有两个交点、一个交点、没有交点?

分析考察图1，直线l是含参数k(扮演角色是直线的斜率)过点P(2,3)的直线系．与圆的位置关系可用《几何画板》软件的动画让直线l运动起来,通过观察,找到直线l与圆相交时的临界位置(无交点↔有一个交点↔ 有两个交点↔ 有一个交点↔没有交点)，经过这样一个过程,容易得到相切时直线斜率k的值是临界位置的k值，从而易得结论．

变题1 (考察图2)，m为何值时，直线l:x+y-m=0与圆x2+y2=1有两个交点、一个交点、没有交点?

设计意图变题1是改变直线l的方程,引进新的参数m(扮演的角色是直线l的纵截距)，通过探究直线与圆的位置关系找临界位置,观察直线l的纵截距的变化过程．

变题2改变曲线的方程(由圆变成半圆)观察直线与曲线的位置关系及交点变化情况．

变题3改变曲线方程,再改变直线方程,观察直线与曲线的位置关系及交点变化情况,研究直线l的纵截距的变化过程．通过改变题设条件更深入地理解问题的本质．

解决直线与圆位置关系的问题关键在于利用数形结合找临界位置，把握参数在直线中扮演的角色．通过改变题目的题设条件,消除同学对题目的神秘感,培养和锻炼让学生动态地全面地认真问题的本质.这样做，有利于加强学生知识的横向和纵向的知识的联系，有利于调动学生探索问题的积极性,可使学生感到出题和解题的乐趣，感受数学的内在美，提高学生的思维品质．将题目改造过程有计划地展示给学生，学生学习积极性,提高效果明显,加之《几何画板》动态地演示更加激发学生的学习兴趣,激发学生的创新思维．

3.通过一题多解,训练学生思维的多向性

例3已知圆C:(x-1)2+(y-2)2=16,直线l:mx+3y-4m-6=0.

(1) 证明:直线l与圆相交；

(2)求直线l被圆C截得的弦长最小(最大)时,直线l的方程.

分析第(1)问学生易从直线与圆位置的位置关系d与r的关系判断．证明直线l与圆相交,即d

第二种方法:直线l含参数m, 通过前面所学知识可知直线l必过定点P(4,2),可从另一方面着手,看点P与圆的位置关系(点P在圆内,过点P直线必与圆相交;点P在圆上,过点P的直线与圆可相交或相切;点P在圆外,过点P的直线与圆可以相交、相切或相离)从而由点P在圆内进行证明．

对于第(2)问，学生易从直线l动态变化的过程中,直观观察出当直线l与圆心C和点P的 连线CP垂直时(如图5),弦AB最短;过圆心C时,弦AB最长．圆的弦中直径最长易解释,而为什么当l⊥CP时弦AB最短,不易说明．然而可利用几何图形——直角三角形中线段的大小关系证明垂径定理,很容易说明问题．(利用几何画板的动画证明,简单、直观)

由点到线，再到面，引出如下的思考题:

当直线l倾斜角为何值时,直线l被圆C截得弦与圆心C构成的三角形面积最大?

学生易从求三角形面积着手考虑问题．把AB当作为底(如图6),圆心C到直线l的距离作为高,求解三角形面积，这是最易想到的一般方法．

方法1设直线l的方程为y-2=k(x-4),则圆心到直线l的距离(如图6)为

(到此，学生感到很棘手,对于一个二次函数求最值,是一个难点)

这里通过分解、化难为易、分步处理:

=-9t2+2t+7

(到此学生认为大功告成,回头看解题,会发现设直线里l的方程是点斜式方程,点斜式有其局限性,不能表示斜率不存在的直线．)

纵观上面3种方法,方法1解法最繁冗,但如果改变题设,会发现若直l与圆心构成三角形不能为直角三角形时，方法2,方法3就不再奏效了．因而方法2,方法3解决此问题要有前提条件，方法1是通法．

一题多解,让学生从不同的角度去观察思考数学问题,用学过的不同的知识,达到解题的目的,这样能够训练学生思维的多向性,课堂上学生思维活跃,跃跃欲试.(一位同学,竟联想到补三角形为菱形,当此菱形为正方形时面积最大)

五、教后反思

(1)利用多媒体教学,方法与手段上都丰富了传统教育教学模式．利用几何画板及powerpoint动画效果,增强了同学对几何图形的直观认识．学生很喜欢,学习情绪高涨,表现出极大的热情和一定的创造力．

(2)几何画板在数学课堂上的运用极大地发挥了这一教学软件在解析几何教学中的强大的直观、动态的功能，丰富了课堂气氛,让学生直观感受到了数学的内在美,丰富了课堂内容，学生学习兴趣有明显的提高,课堂思维活跃．

(3)利用多媒体教学增加了学习的趣味性,课堂容量丰富了许多,讲授内容也多了许多．

然而如何让多媒体教学与传统教学合理的融为一体,是我们当前创新教育时代要思考的一个很重要的问题．这就要求我们每位教师对《新课程标准》要有深刻理解,对新课程改革作出积极探索;对传统教育学合理地批判与继承.在实际教学中合理地设计教学,设计教学中学生主体活动的结构,为学生发展开拓有效的活动空间．多使用一些需要学生创造性思考的教学方法,不断培养学生的创新意识,为促进学生的全面发展创造条件．让我们用创造性的教唤起学生创造的学,用我们创造性的思维方法铸起学生创造性的思维品质,让教与学和谐地碰撞出创造的火花．