立体几何中的展开翻折问题探究

魏成年

(甘肃省武威市第六中学,733000)



○数学探究○

立体几何中的展开翻折问题探究

魏成年

(甘肃省武威市第六中学,733000)

立体几何中的最值问题常常需要将几何体或旋转体展开成平面图形(空间问题平面化),利用平面几何的知识来解决.或者将平面图形折叠成立体图形,求解立体图形中的空间角、证明位置关系问题等.这类问题是考查学生空间想象能力与逻辑思维能力的好题,也是高考的热点. 对于这类问题,要结合多面体或旋转体的定义和结构特征,发挥自己的空间想象能力,必要时还可制作平面展开图进行操作实践.在数学教学中要多渠道、多层次通过变式拓展,操作实践,引导培养学生养成观察、操作、探索、合情推理的习惯,形成稳定的空间想象能力.现举例如下.

一、展开图中求“最短”

一般地,多面体或旋转体绕侧面或表面最短距离的问题,除球体外,基本都是通过展开图来解决,关键是找准剪开的线,准确用展开图中的某条线段来表示这个最短距离.另外，这里所谓最短距离,实质是沿多面体或旋转体侧(表)面的最短路径.解题的一般思路是沿着它的某条棱或母线剪开成平面图形,借助这些几何体的展开图，利用“两点之间线段最短”的公理来求解、讨论.

对于此类问题,我们在教学中可以一道例题(如下面的例1)为“母题”,进行变式、拓展,形成问题链.通过对问题链的解决,使学生对多面体或旋转体中的最短距离有一个更深的理解,使每个学生的空间思维得到升华,空间想象能力得到提高.

思路分析解决这类问题的方法就是先把多面体侧面展开成平面图形,再用平面几何的知识来求解.本题中沿点A、P所在侧棱剪开展平,再利用平面几何知识或解三角形知识求解.

在本例的教学中,如果平铺直叙地给出展开图,学生很难留下深刻的印象.为了增加学生对数学的兴趣,培养学生对数学的探究精神,老师可以带领学生创设情境(如求一只蚂蚁在三棱锥表面爬行一周又回到出发点的最短距离),从创设的问题出发,动手探索,使学生对最短距离问题有更深的理解、记忆,从而达到良好的教学效果

变式1(棱柱上沿侧面行程的距离最短问题)在三棱柱ABC-A1B1C1中,侧棱AA1垂直于底面,且侧棱AA1=5,底面ABC是边长为2的正三角形,求从点A出发沿三棱柱表面绕两周到达点A1的最短距离.

思路分析有了例1的探究、分析、解答,学生容易将三棱柱沿AA1展开,可利用勾股定理易得从点A出发沿三棱柱表面绕两周到达点A1的最短距离为13.

变式2如图3,长方体ABCD-A1B1C1D1中,AB=a,BC=b,BB1=c,并且a>b>c>0，求沿着长方体的表面自A到C1的最短线路的长.

思路分析在长方体的展开图中,沿着不同的棱展开会得到不同的结论,因此,对于这类问题,需分类展开分类讨论.

解将长方体相邻两个面展开有三种可能,如图4,三个图形(1)(2)(3)中，AC1的长分别为:

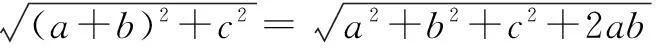
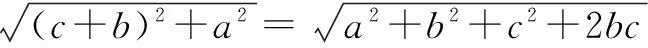
∵a>b>c>0，

∴ab>ac>bc>0.

思路分析圆锥上沿侧面行程的距离最短问题与棱锥上沿侧面行程的距离最短问题是相似的,类比棱锥中求展开图的两点间的距离,在圆锥中便是求侧面展开图中扇形的圆心角所对的弦长,利用平面几何知识可轻松得解.

变式4圆柱的轴截面是边长为5 cm的正方形ABCD,圆柱侧面上从A到C的最短距离是多少?

思路分析展开圆柱的侧面,其侧面为矩形,则在侧面上从A到C的最短距离就是对角线AC的长.

通过上面的变式探究,学生对于多面体或旋转体中绕侧面或表面最短距离的问题就不会陌生,思路一旦打开,一种柳暗花明的感觉就油然而生.

二、翻折问题找“不变”

解决翻折问题在于画好翻折前后的图形,寻找折痕以及与折痕相关的量,分清各元素在翻折前后的“变”与“不变”.一般情况下,在折线同侧的量,折叠前后不变,“跨过”折线的量,折叠前后可能会发生变化，这是解决这类问题的关键. 另外,在解题时还要仔细审视从平面图形到立体图形的几何特征的变化情况,注意相应的点、直线、平面间的位置关系,线段的长度、角度的变化情况.

例2如图7所示,在Rt∆ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将∆ADE沿DE折起到∆A1DE的位置,使A1F⊥CD.

(1)求证:DE∥平面A1CB;

(2)求证:A1F⊥BE;

(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ? 请说明理由.

思路分析在本题的折叠前后有,平行不变量DE∥BC;垂直不变量DE⊥A1D，DE⊥CD,DC⊥BC;长度不变量AD=A1D=DC,弄清了这些不变的量,解答题目就不会感到困难.

解(1)证明:因为D,E分别为AC,AB的中点,所以DE∥BC.

由平行不变量DE∥BC，

又DE⊄面A1CB,所以DE∥平面A1CB.

(2)证明:由垂直不变量DE⊥A1D、DE⊥CD,且AD∩CD=D,所以DE⊥面A1DC,

而A1F⊂面A1DC,所以DE⊥A1F.

又因为A1F⊥CD,所以A1F⊥面BCDE,所以A1F⊥BE.

(3) 线段A1B上存在点Q,使A1C⊥面DEQ.

理由如下:

如图8所示,分别取A1C、A1B的中点P、Q,连结DP,PQ,QE,则PQ∥BC.

又由平行不变量DE∥BC,

所以DE∥PQ,所以平面DEQ即为平面DEP.

由(2)知,DE⊥面A1DC,所以DE⊥A1C.

由长度不变量AD=A1D=DC,所以P是等腰∆DA1C的底边A1C的中点,所以A1C⊥DP,所以A1C⊥平面DEQ.

故线段A1B上存在点Q,且Q为A1B的中点时,使得A1C⊥面DEQ.

在数学教学中,老师的责任就是引导,引导学生对折叠前后图形的元素进行分析,分清不变量与变量,深刻理解折叠前后图形中元素不变的原因,提高学生的空间想象能力,力争使学生对空间图形的剖析认识上升一个台阶.

总之,立体几何中的这些问题,只要我们善于归纳、总结,按照“直观感知、操作确认、思辨论证、度量计算”的思路,理清折叠、展开的相互联系,立体几何的学习就会成竹在胸、得心应手.