一道课本例题的应用探究
钟时泉
(广东省惠州市第一中学,516007)
一道课本例题的应用探究
钟时泉
(广东省惠州市第一中学,516007)
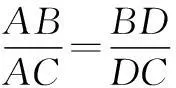
这是个初中和高中都没有直接给出的重要定理,在高中教材中也只是以一个例题形式出现.但它的应用是广泛的.下面就其四个方面的应用加以介绍,仅供参考.
一、倍角与半角
以必修2练习中出现的两个习题为例,按照5个必修课本的使用顺序1-4-5-2-3,在此时学习完了三角函数的半角与倍角公式,用三角函数公式来解,简单快捷.但如果按照教材编排的顺序和不把必修4的内容提前讲,那么碰到这类题很多教师都删了.教材编写者认为放在这里肯定没有问题的,通过初中学过的平面几何知识可以很巧妙地解决这类问题.
例1已知两点A(-2,-10),B(6,-4),直线l的倾斜角是直线AB的倾斜角的一半,求直线l的斜率.
如图1,作直角∆ACB,AD是∠A的平分线,其中点C(6,-10).
由勾股定理,得AB=10,
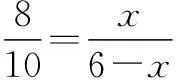
例2一条直线l经过点P(2,1),并且满足倾斜角是直线l1:x-4y+3=0的倾斜角的两倍,求直线l方程.

如图2,作直角三角形ACB,AD是角A的平分线,其中点A(-3,0),C(1,0),D(1,1).
设BD=x,则AB=4x.又由勾股定理,得
(4x)2=42+(x+1)2,
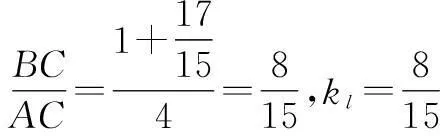
又直线l经过点P,所以直线l的方程为8x-15y-1=0.
二、求轨迹方程
我们知道,设动点P与两个定点A,B的距离的比为定值λ,若λ=1,则动点P的轨迹是线段AB的垂直平分线;若λ≠1,则动点P的轨迹是圆.因此,可以通过用坐标法求出动点P的轨迹方程,进而说明轨迹形状.下面从几何角度求出动点P的轨迹.
例3已知定点A(-2,0),B(1,0),动点P与A,B两点的距离的比为2∶1,求动点P的轨迹方程.

因此,P的轨迹是以N为圆心,2为半径的圆,所以动点P的轨迹方程为(x-2)2+y2=4.
三、三角形内心的向量式
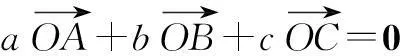
(A)内心(B)外心(C)重心(D)垂心

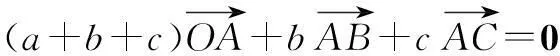
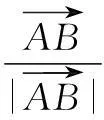
四、在高考解题中的应用
华南师范大学蔡润芳老师在《数学通讯》2012(4)20-21一文中探究了圆锥曲线焦点三角形顶角平分线的性质,得到以下结论:
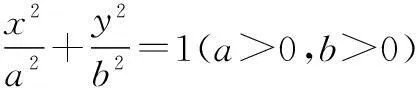
由此还可得到结论:
椭圆的焦点三角形的顶角P的角平分线与椭圆在点P的切线互相垂直.
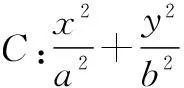
(1)若点Q的坐标为(4,4),求椭圆C的方程;
(2)证明:直线PQ与椭圆C只有一个交点.

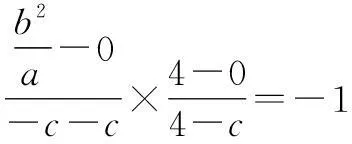
①

②
c2=a2-b2(a,b,c>0).
③

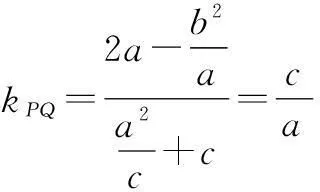
由上面的结论,可知∠F1PF2的角平分线所在直线的斜率为

所以直线PQ与∠F1PF2的平分线垂直,所以PQ为椭圆的切线,所以直线PQ与椭圆C只有一个交点.
本题主要考查椭圆方程和椭圆的几何性质,直线与椭圆的位置关系等基础知识,总体难度不大.第(2)问可以直接通过直线PQ方程和椭圆方程联立求解,而通过上面的结论则从几何方面揭示了该题的背景.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连结PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围.


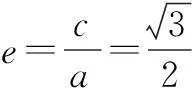

(2)若运用夹角公式或到角公式进行条件转化的思路,同样可以得到m与x0的式子,但化简过程是一难题,所以可以考虑用角平分线的性质去解题.因为PM是∠F1PF2的角平分线,所以在ΔF1PF2中,有
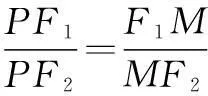
设P(x0,y0) (y0≠0),则由椭圆焦半径公式,得
PF1=a+ex0,
PF2=a-ex0,