两相均流板对弯管中气固两相运动分布特征的影响

潘晓慧，马春元，崔琳（山东大学燃煤污染物减排国家工程实验室，山东 济南 250061）



两相均流板对弯管中气固两相运动分布特征的影响

潘晓慧，马春元，崔琳
（山东大学燃煤污染物减排国家工程实验室，山东 济南 250061）

摘要：针对燃煤电厂烟气污染物脱除设备入口弯管内气固两相分布不均的问题提出一种新型两相均流板，采用CFD数值模拟首先对比分析了安装两相均流板与常规导流装置的均流效果，之后详细研究了新型两相均流板对弯管水平出口管道中气流速度、颗粒质量分布规律的影响以及板型及板间夹角对两相均流板均流效果的影响，并结合Design-Expert响应面法获得两相均流板的最优结构，将最优结构应用于工业性实验中，最后将计算结果与工业性实验数据进行了比较。结果表明：弯管内安装两相均流板较安装导流板/三角翼挡板气固两相均流效果更优，既可以使气固两相均匀分布又可以有效降低系统的压阻；随板间夹角的增大，管内的气流速度分布以及颗粒的质量浓度分布呈阶段性变化，而管内的压降则随板间夹角增大而增大；最佳两相均流板结构为夹角为75.49°的直板型两相均流板。模拟与实验结果吻合较好，利用提出的数值模拟方法可以详细真实地模拟计算大型及具有复杂内部结构的除尘器入口弯管中气固两相流动。

关键词：两相流；弯道；数值模拟；均化；分布

2015-11-02收到初稿，2016-02-27收到修改稿。

联系人：马春元。第一作者：潘晓慧（1987—），女，博士研究生。

Received date: 2015-11-02.

Foundation item: supported by the National Natural Science Foundation of China (51006063), the Shandong Province Natural Science Foundation (2014EEM040), the Shandong Province Independent Innovation Foundation (2014ZZCX05201) and the Fundamental Research Funds of Shandong University (2014QY001-04).

引　言

受空间布置的限制，弯管在燃煤电厂烟气污染物脱除系统中广泛应用，由于气固两相流场的流动特性十分复杂，出现回流、偏流等问题[1-4]，易在管壁附近形成分离区，管道横截面上产生二次流动，同时受惯性影响，颗粒通常在弯道外侧聚集，导致设备入口的气固两相分布不均匀[5-9]。

目前多采用导流板、三角翼挡板等常规均流装置进行均流处理。弯道中安装导流板可达到均匀气体速度的目的，但颗粒在导流板近壁区富集，导致多个板间通道内气固两相分布不均，影响后续设备工作效率。如SCR脱硝入口气固两相不均造成催化剂局部磨损严重，对气体污染物扩散阻挡不均而脱除反应不均，干/湿式静电除尘器入口气固两相不均致使除尘器内部颗粒荷电不均、团聚与分离效果不佳[10-15]。弯道中安装三角翼挡板，其钝体结构可以优化挡板后气固两相均布效果，但同时极大地增加了系统的压阻。如在600 MW电厂SCR烟气脱硝反应器入口烟气管道内安装三角翼挡板，随着安装角度的减小，气固混合作用增强，但烟道进出口的压降相对增加了80%～140%[16-19]。

为解决上述问题，本文提出一种迎风面流线体背风面钝体结构的两相均流板，以克服常规均流装置气固两相均流效果不佳、阻力大等缺点，期望在较低的压阻下解决燃煤电厂烟气污染物脱除系统入口气固两相混合不均匀的问题，有效提高污染物脱除效率。

1　计算模型与计算方法

本文提出的两相均流板的具体结构如图1所示。整个均流板由前端导流板部分和后方涡街发生体部分构成，涡街发生体的结构分为直板型、弧板型和曲板型，其尺寸随板间夹角θ变化。将两相均流板置于90°方形弯管中，具体的几何模型如图2 （a）所示（以θ=30°的直板型两相均流板为例）。为了便于模型验证，以300 MW燃煤机组电除尘器入口处直角弯管原型为几何研究对象，将弯管分成入口垂直段、弯曲段和出口水平段3部分，弯管的方形横截面尺寸为4800 mm×3600 mm，水力直径D为1441 mm，弯管段的曲率直径比为Rc/D=1.17，曲率半径Rc为4800 mm。为了更准确地了解整个出口管道的气流分布状况，根据GB/T 16157—1996《固定源排气中颗粒和气态污染物的采样方法》中的规定，在水平出口段取6个观测横截面，具体位置如图2(a)所示。

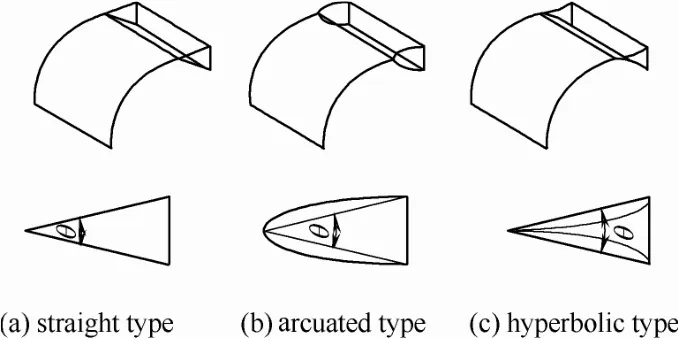
图1　两相均流板结构Fig. 1　Schematic diagram of structure of two-phase deflector (Above: three-dimensional structure. Below: two-dimensional cross-sectional structure)

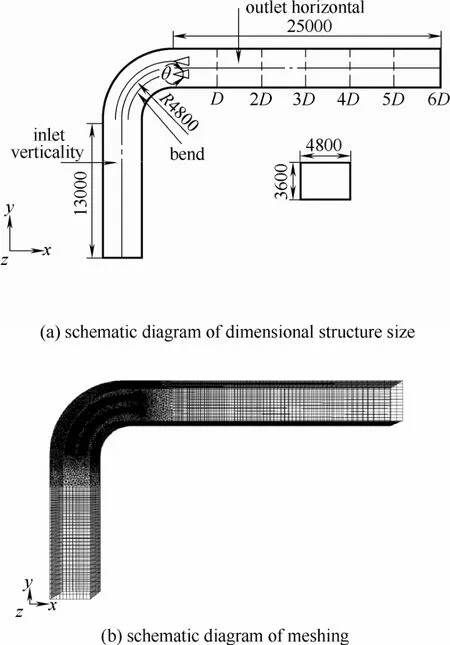
图2　计算模型Fig.2　Schematic diagram of simulation model

通过前处理软件GAMBIT进行网格划分，入口垂直段和出口水平段均采用正六面体结构化网格，弯曲段采用size function对两相均流板附近进行网格加密处理，最终网格生成图如图2（b）所示。以板间夹角为30°的直板型两相均流板为例，通过调整网格数量对模拟结果进行对比验证，综合考虑求解精度和计算耗时等因素，当模拟结果随网格数量的增加误差不超过2%时获得网格独立解，此时网格总数为2.422×106个。

管内气固两相流假设为稳态不可压缩流。采用Euler-Lagrange方法对气固两相流进行模拟，即连续相气相采用Euler方法模拟，固体颗粒相采用Lagrange方法模拟。由于颗粒在气流中的容积含率小于10%，采用气固双向耦合方法模拟，即模型考虑气固之间的相互作用而忽略颗粒间的相互碰撞作用，湍流模型采用标准k-ε方法。

模拟选用的流体为常温状态下空气，密度为1.225 kg·m−3，黏度为1.7894×10−5kg·m−1·s−1；入口选择速度入口，入口流速10 m·s−1；出口边界条件选择压力出口，压力为大气压。固体颗粒密度为1770 kg·m−3，粒径取0～200 μm，采用Rosin-Rammler正态分布，入口速度取10 m·s−1，质量流量为8 kg·s−1（相当于入口颗粒相体积分数0.126%，入口体积流量30 g·m−3），同时采用随机轨道模型考虑颗粒的湍流扩散作用，将出口设为颗粒完全逃逸，颗粒轨道计算在出口处终止。在弯管的壁面部分和均流板的壁面位置，气相采用无滑移边界条件，应用标准壁面函数法近似处理近壁网格区域。颗粒与壁面之间的作用通过碰撞恢复系数描述，采用Jun等[20]提出的反弹经验公式预测颗粒与壁面的碰撞过程，表达式如式（1）所示

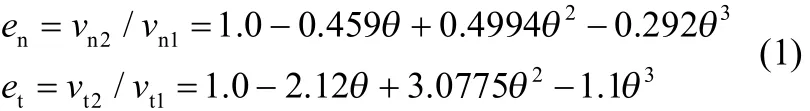
式中，vn1、vn2、vt1、vt2分别为颗粒碰撞壁面前后法向与切向的分速度，en为法向恢复系数，et为切向恢复系数，θ为颗粒的撞击角。

2 计算结果与分析

2.1两相均流板与常规均流装置的均流效果对比分析

分别模拟了弯管中不安装导流装置（a）、安装常规导流板（b）、安装三角翼挡板（c）及安装两相均流板（d）4种情况（考虑到4种情况之间的可比性，设定常规导流板与两相均流板前端导流板尺寸相同，三角翼挡板与两相均流板后方涡街发生器迎风面阻挡面积相等）下管内的气固两相流速度、浓度和压强分布，对模拟结果进行对比分析，并根据JB/T 7671—2007计算气流速度/浓度标准偏差系数，对气流速度/浓度优劣做出判定。

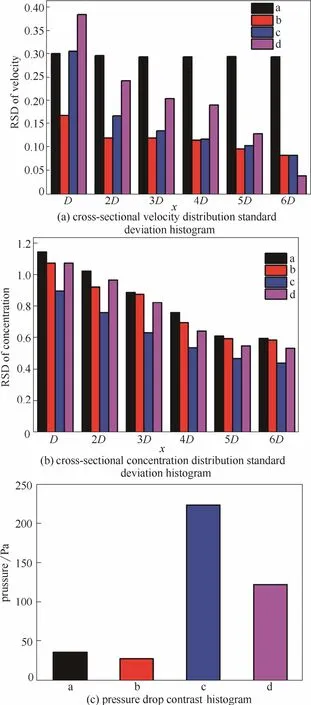
图3　两相均流板与常规均流装置的均流效果模拟计算结果Fig.3　Simulation result of flow uniform effect of two-phase deflector and conventional deflector

计算结果如图3（a）、（b）所示。由图3（a）可以看到，弯管中安装导流板后速度分布状况最优，安装两相均流板及三角翼挡板后在弯管后较短距离内速度分布均匀性较差，但随着气流的发展速度分布逐渐趋于均匀，而且标准偏差均在0.25以下，速度分布均匀性良好，在出口处基本与导流板的均匀效果一致；如图3（b）所示，在整个出口管道中颗粒质量浓度分布优劣状况为c＞d＞b＞a，两相均流板对气固两相质量浓度均流效果仅次于三角翼挡板；如图3（c）所示，在弯管内安装两相均流板后整个管内的压降较管内安装三角翼挡板降低50%左右。综合分析可知，处理装置入口气固两相流的均流问题时，导流板、三角翼挡板和两相均流板均可以保证弯管内气流速度分布均匀，但两相均流板/三角翼挡板对颗粒分布的均匀性更优，而两相均流板较三角翼挡板有更低的管内压降。因此，在弯管内安装两相均流板较安装导流板/三角翼挡板更优，既可以使气固两相均匀分布又可以有效降低系统的压阻。

2.2安装两相均流板后弯管内运动分布特征

通过以上分析可知，两相均流板与常规导流板/三角翼挡板相比，对气固两相流进行均流处理时效果更佳。以涡街发生体板间夹角30°为例进一步详细模拟分析了弯管内安装两相均流板后管内气固两相运动分布特征，结果如图4～图6所示。

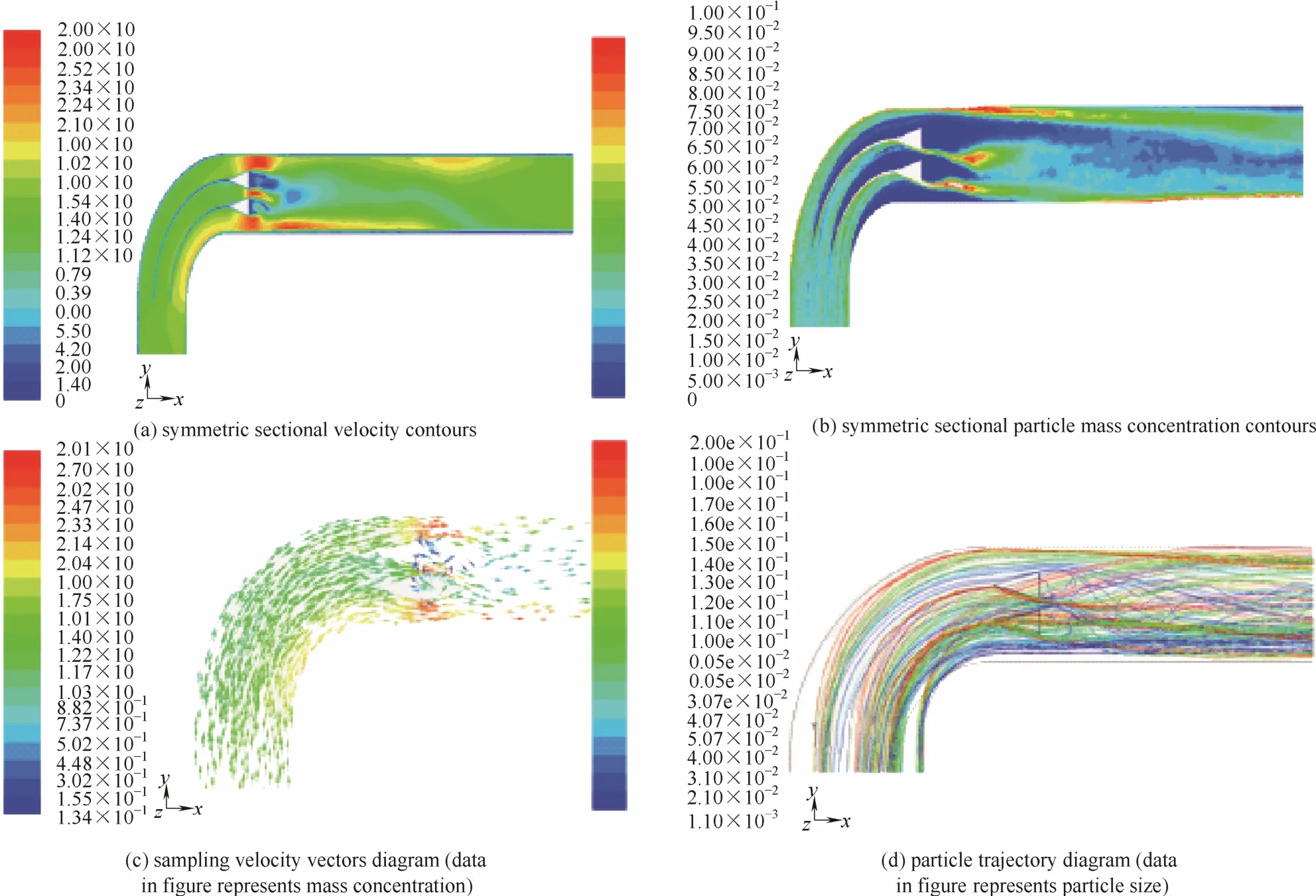
图4　气固两相分布特征计算结果Fig.4　Simulation results of distribution characteristics of gas-solid two-phase flow

图4（a）给出了弯管对称截面气流速度分布云图。弯管段后方布置数个涡街发生体，气流经过迎风面流线体结构并逐渐向背风面钝体结构过渡的过程中管内流通面积随之减小，在经过背风面钝体结构后管内流通面积恢复，在此过程中管内流通面积经历了由大变小又变大的过程。在流通面积由大变小阶段，气流速度逐渐增大，呈喷射状冲入水平直管段，同时由于背风面钝体结构的阻挡作用其后方出现小区域的低速区，但随着气流逐渐发展，在水平管段气流速度分布变得十分均匀。

图4（b）、（c）为弯管对称截面颗粒质量浓度分布云图以及弯管局部速度矢量图。可见在弯管段颗粒主要集中于前置导流板的贴壁处，远离导流板处形成较小的低浓度区。在进入水平直管段后，气流在流经涡街发生体之间以及涡街发生体与管壁之间形成的狭小通道时颗粒出现富集现象。同时涡街发生体的背风面钝体结构后方产生较大区域的低浓度区，而且此区域的颗粒多为小粒径颗粒[如图4（d）所示，多为0.06 mm以下]，但由于钝体结构的作用，板后产生连续涡街，如图4（d）所示，气流在涡街作用下发生紊流扰动，使此区域颗粒质量浓度分布较为均匀，可在两相均流板后的较短距离内（x=0～D）形成均匀的低颗粒质量浓度区。之后，随着涡街发生体后流通面积增大，颗粒质量浓度逐渐增大，在水平管段颗粒质量浓度逐渐变得均匀。

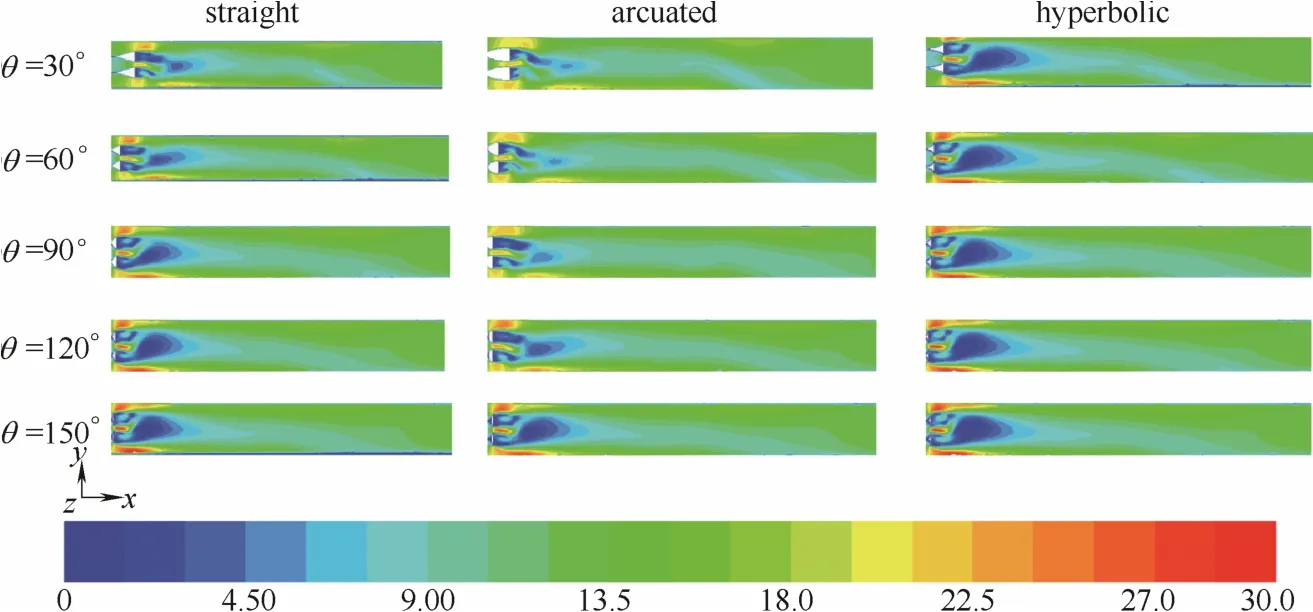
图5　水平出口管段对称截面气流速度分布云图Fig.5　Velocity contours of longitudinal cross-section of horizontal pipe

图6　水平管段颗粒质量浓度分布云图Fig.6　Concentration contours of longitudinal cross-section of horizontal pipe

2.3不同板型及板间夹角对两相均流板均流效果影响分析

图5和图6为两相均流板板间夹角从30°增大到150°的过程中不同的涡街发生体板型（直板/弧板/曲板）对气固两相流在管内的速度、浓度和压强分布的影响。

图5给出了水平出口管段对称截面气流速度分布云图。弯管中安装不同板型的涡街发生体后，在涡街发生体后方短距离（x=0～D）内速度分布有明显的差别，管道中心位置会产生小区域的低速区，曲板型涡街发生体后方产生的旋涡湍动性强，旋涡的卷吸作用导致旋涡中心区域的低速区增大，而且随着气流的发展旋涡的衰减过程较长，在涡街发生体后方产生一个范围相对较大的低速区，相比之下，直板型涡街发生体后方的低速区范围较小，弧板型涡街发生体后方的低速区范围最小，此阶段随着板间夹角的增大低速区范围逐渐扩大，气流速度分布均匀性逐渐变差。x=D～6D段，沿水平管速度分布特征基本相似，随着板间夹角的增大气流速度分布越来越均匀。其中，x=D～4D段，气流速度由中心向两侧逐渐增加；x=4D～5D段，气流速度由管道上侧向下侧逐渐降低，在板型引起的管内压强分布差异以及出口大气压的综合影响下管道上侧出现不同范围的局部高速区，但随着板间夹角的增大管道内部压强分布随之发生变化，高速区逐渐减小，在板间夹角增大到150°时基本消失，其中安装曲板型两相均流板的弯管内此处高速区最小，气流分布均匀度最佳，直板型次之，弧板型最差；x=5D～6D段，管内速度分布均已呈现均匀状态。

图6（a）和图6（b）给出了水平出口管段对称截面以及横截面颗粒质量浓度分布云图。如图所示，在涡街发生体后方产生的旋涡作用及弯道后方的射流作用的综合影响下水平管段的颗粒质量浓度分布趋势相似，局部略有不同。水平管段x=0～D段，涡街发生体后方产生的旋涡对颗粒质量浓度分布有较大的影响，根据以上分析的不同板型的涡街发生体后方旋涡的湍动性强弱程度、产生位置和持续范围来看，曲板型均流板后方的颗粒分布最为均匀，截面颗粒质量浓度从中心向边界逐渐递增；弧板型均流板后方的颗粒分布均匀程度最差，截面颗粒浓度分布呈上、下两部分，上部浓度小而下部浓度大，由此也可以看出弧板型均流板对板后的气流的扰动程度较弱，不足以达到使颗粒均匀分布的目的；直板型均流板后方的颗粒分布均匀性居中，颗粒质量浓度分布趋势与曲板型均流板相似，但由浓度中心向边界递增的过程中梯度更大，而且在界面底部出现小面积高浓度区。水平管段x=D～6D段，颗粒质量浓度分布趋势基本一致，随着气流向出口发展的过程，管道上部的高浓度区域逐渐减小且浓度逐渐降低，管道下部颗粒质量浓度逐渐增大，到出口处时上部和下部的颗粒浓度基本一致。由于弧板型均流板对板后的气流的扰动程度较弱，射流作用在此阶段仍然对颗粒质量浓度分布有影响，相对其他板型的均流板，弧板型均流板后方管道上部颗粒高浓度区范围更大，均流效果最差。

随着板间夹角的增大，板前方的流线体的降阻作用减弱，气流对均流板迎风面的冲击力增加，均流板对气体的扰动作用增大，在气流经过弯管后产生的射流作用的综合作用下颗粒沿流线体下方的聚集程度逐渐增加，板后较短距离x=0.5D处截面中心出现的高浓度区的浓度呈递增趋势；x=0.5D～D段，截面中心的局部高浓度区在板后的旋涡的作用下开始扩散，随着板间夹角的增大板后的旋涡的湍动作用增大，产生的扩散作用增强，中心高浓度区完全扩散开的距离减小。在板间夹角达150°时，板后的旋涡的扩散作用最剧烈，局部高浓度区在最短的距离内就完全扩散开，在x=D界面处整个截面的浓度分布已经十分均匀；随后x=D～6D段，均流板的扰动作用和气流的射流作用随气流流动方向逐渐减弱，颗粒自身的重力作用和扩散作用逐渐增强，整个管道的气流速度分布呈现出由上侧向下侧递减的趋势，随着板间夹角的增加，截面上方的浓度逐渐减小，截面下方的浓度逐渐增加，整个截面的浓度梯度减小，分布更加均匀。

图7给出了安装不同板型及板间夹角均流板的管道内压降变化曲线。管内安装三角翼挡板时，随着板间夹角的增大，均流板前方的流线体的有效迎风面积增大，整个管道的有效流通面积随之减小，整个管道的压阻随之呈直线上升趋势，直板型和弧板型均流板使管内压降随板间夹角的增大而剧烈变化，曲板型则随板间夹角的增大变化不明显，弯管中压阻大小排序为弧板型＞直板型＞曲板型。安装曲板型两相均流板后弯管进出口压差较大的主要原因在于曲板的前方与空气的接触面积较大，而且曲板形状会导致空气在流经曲面时产生一个向后的卷吸力，进一步增加气流流动阻力，从而增加了管内压差。

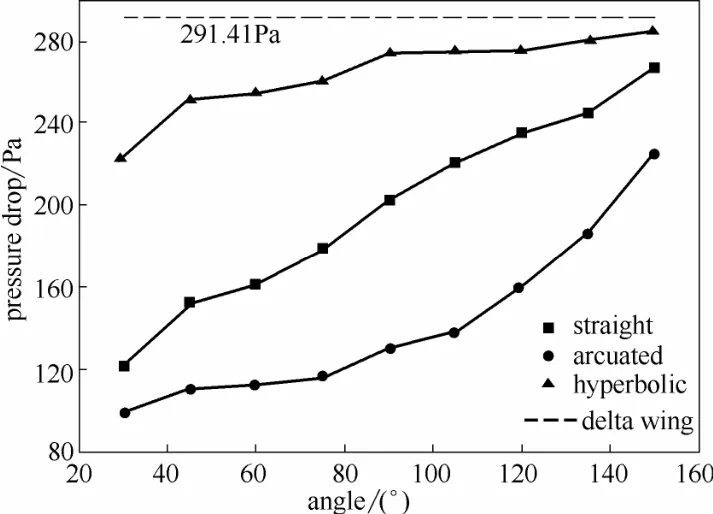
图7　管道内压降变化曲线Fig.7　Pressure drop profile of elbow

3　两相均流板结构优化分析

利用CFD软件计算模拟弯管中安装不同板型及板间夹角的两相均流板时管内气固两相运动分布特征，将速度、浓度和压降值进行标准偏差系数计算，并将计算结果进行比较分析。图8（a）和图8 （b）给出了不同的板型和板间夹角情况下速度与浓度分布标准偏差柱状图。结合以上的压降变化曲线图（图7）可以看出，不同形状的涡街发生体对管内速度、浓度和压降的影响程度各不相同，涡街发生体为弧板型时管内气流速度分布最均匀，直板型次之，曲板型最差；涡街发生体为曲板型时管内颗粒质量浓度分布最均匀，直板型次之，弧板型最差；涡街发生体为曲板型时管内压降最大，直板型次之，弧板型最小，但均小于安装三角翼挡板的管内压降。虽然管内安装曲板型两相均流板气固两相均流效果最佳，但管内压阻最大；弧板型两相均流板的管内压阻最小，但两相均流效果最差；直板型与曲板型两相均流板的管内均流效果相似，但随着板间夹角的减小，直板型较曲板型进出口压降相对减少25%～45%。同时可以看到，板间夹角的变化也会影响管内速度、浓度和压降的变化，随着板间夹角的增大，管内的速度和浓度的分布呈阶段性变化，但整个变化趋势基本遵循板间夹角越大均匀程度越差的规律；管内的压降随板件夹角的增大呈直线上升趋势，直板型和弧板型均流板会使管内压降随板间夹角的增大而剧烈变化，曲板型则随板间夹角的增大变化不明显。

图8　横截面速度、浓度计算结果Fig. 8　Simulation results of velocity vectors and particle concentration of cross-section

安装两相均流板要达到最佳效果，必须满足气流速度分布均匀、浓度分布均匀，而且在此前提下保证管内压降最小。从以上分析可知，板型和板间夹角会对管内气流速度和颗粒质量浓度分布均匀性以及管内压降产生不同程度的影响，有利有弊，对速度分布均匀性、浓度分布均匀性以及管内压降赋予不同的权重，满足条件的最优结构随之不同。考虑到本研究的目的是克服三角翼挡板导致管内压降过大的缺点，将压降变化产生的影响赋予最高权重，同时保留三角翼挡板对颗粒质量浓度有较好均匀效果的优点，将管内颗粒质量浓度的分布均匀性赋予第二位权重。以此为判断依据，使用软件Design-Expert（美国Stat-Ease公司开发的实验设计软件系统，该软件在各类多因素实验设计和分析领域应用广泛）对实验数据进行统计分析、拟合曲线、建立数学模型并给予期望函数进行多目标优化，当速度标准偏差RSDv、浓度标准偏差RSDc和压降∆p最小化时两相均流板的结构为最优。设置两相均流板的压降标准偏差、浓度标准偏差与速度标准偏差的权重系数分别为5、4、3（权重系数的取值范围为1～5，默认取值为3，该系数表示多个响应之间的优先级，数值越大优先级越高[21]），预测响应值的期望用式（2）进行定义[22]

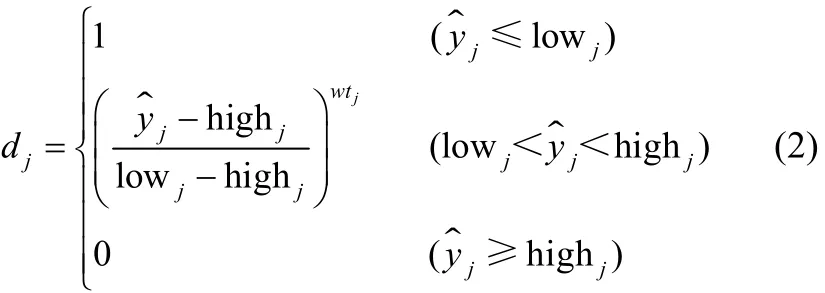
式中，lowj和highj分别是第j个响应的最小值和最大值；wtj为权重；dj是计算获得的第j个响应期望值，期望值的取值范围从0（响应值在不能接受的范围内）到1（响应值为最优）。

表1　通过期望函数获得的最优设计参数Table 1　Optimum design parameters obtained by desired function

表1给出了不同板型条件下系统推荐的同时满足较低压降标准偏差值、较低浓度标准偏差值与较低速度标准偏差值的优化结构尺寸，由表中期望值可以看出，当两相均流板的板型为直板型，板间夹角为75.49°时，期望值最高，为最优结构。

4　数值模拟结果与测试结果的对比验证

为了验证数学模型的正确性和计算方法的准确性，利用本研究建立的模型计算弯管内安装最优两相均流板结构（涡街发生体板间夹角75.49°）时管道内气固两相流的运动特性，同时将最优结构应用于300 MW燃煤机组电除尘器入口处直角弯管内，分别使用热风测速仪、ELPI和烟尘平行采样仪现场测量弯管段后方相连的直管段各截面的速度、颗粒浓度与压强分布，将计算结果与工业性实验现场的测试结果进行对比分析。

在气流分布均匀性的实验中，利用微压计和崂应3012H型自动烟尘（气）测试仪对直管段各截面的气流速度和浓度分布情况进行了现场测量。沿气流运动方向布置6个测试面(D，2D，3D，4D，5D，6D），每个测试面上测点布置为沿直管段高度方向(y方向)均匀布置8排、沿宽度方向(z方向)均匀布置8排，分别对比分析了各个截面上的气流速度分布与颗粒质量浓度分布的实验结果与模拟结果。以3D截面为例，图9显示了沿高度y方向和宽度z方向气流速度分布与颗粒质量浓度分布的实验结果与模拟结果的对比情况，由图可以看出现场测得的数据和模拟数据基本吻合，反映的出口直管段3D截面处的气流速度和浓度分布规律与以上分析的气固两相流的运动特性结果一致。同时在现场实验中利用烟尘平行采样仪对进、出口阻力分布情况进行了现场测量（118.20 Pa），与模拟结果（121.3573 Pa）相对比，误差为2.6%，也基本吻合。

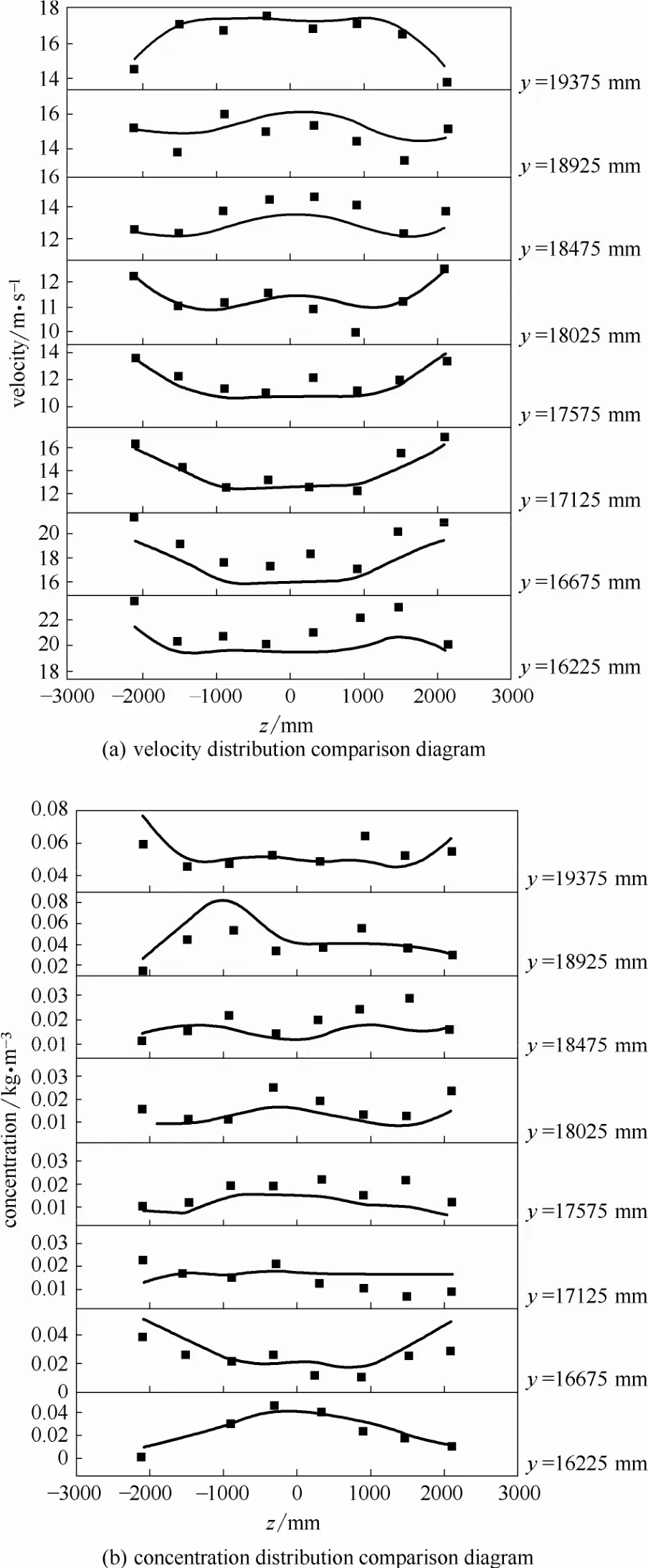
图9　数值模拟与实验结果的对比Fig.9　Comparison diagram of numerical and experimental results at outlet— numerical results；• experimental results

根据现场测得的数据分别计算各截面气相速度标准偏差与截面颗粒质量浓度标准偏差，与模拟结果对比，结果见表2。二者平均误差均为2%左右，均在可接受范围内，说明利用此数值模拟方法，采用与300 MW燃煤机组电除尘器入口处直角弯管原型完全相同的几何模型，可以详细真实地模拟安装有两相均流板的弯管中气固两相运动分布特征，模拟结果与现场实验结果吻合较好，证明了该方法可以很好地应用于大型及具有复杂内部结构的除尘器入口弯头的真实细致模拟。

表2　数值模拟与实验结果标准偏差对比Table 2　Numerical and experimental results of RSD

5　结　论

（1）利用本研究提出的数值模拟方法可以详细真实地模拟计算大型及具有复杂内部结构的除尘器入口弯管中气固两相流动，模拟计算结果与现场测试结果吻合较好。

（2）在弯管内安装两相均流板较安装导流板/三角翼挡板更优，既可以使气固两相流均匀分布又可以有效降低系统的压阻。

（3）管内安装曲板型两相均流板时气固两相均流效果最佳，但管内压阻最大；管内安装弧板型两相均流板时管内压阻最小，但两相均流效果最差；直板型与曲板型两相均流板的管内均流效果相似，但随着板间夹角的减小，直板型较曲板型进出口压降相对减少25%～45%。

（4）随着板间夹角的增大，管内的气流速度分布以及颗粒质量浓度分布呈阶段性变化，而管内的压阻则随板间夹角的增大而增大。

（5）满足较低压降标准偏差值、较低浓度标准偏差值与较低速度标准偏差值的结构为板间夹角为75.49°的直板型两相均流板。

References

[1]XU C, LIANG C, ZHOU B, et al. HHT analysis of electrostatic fluctuation signals in dense-phase pneumatic conveying of pulverized coal at high pressure [J]. Chemical Engineering Science, 2010, 65(4): 1334-1344.

[2]JASSIM E, BENSON S A, BOWMAN F M, et al. The influence of fragmentation on the behavior of pyrite particles during pulverized coal combustion [J]. Fuel Processing Technology, 2011, 92(5): 970-976.

[3]CHINNAYYA A, CHTAB A, SHAO J Q, et al. Characterization of pneumatic transportation of pulverised coal in a horizontal pipeline through measurement and computational modelling [J]. Fuel, 2009, 88(12): 2348-2356.

[4]DRITSELIS C D, VLACHOS N S. Large eddy simulation of gas-particle turbulent channel flow with momentum exchange between the phases [J]. International Journal of Multiphase Flow, 2011, 37(7): 1-16.

[5]AKILLI H, LEVY E K, SAHIN B. Gas-solid flow behavior in a horizontal pipe after a 90° vertical-to-horizontal elbow [J]. Powder Technology, 2001, 116(1): 43-52.

[6]YILMAZ A, LEVY E K. Formation and dispersion of ropes in pneumatic conveying [J]. Powder Technology, 2001, 114(1): 168-185.

[7]蔡杰, 钟文琪, 袁竹林. 提升管内细长颗粒流化运动的气固多向耦合模型的构建 [J]. 化工学报, 2015, 66(11): 4342-4350.DOI: 10.11949/j.issn.0438-1157.20150445. CAI J , ZHONG W Q, YUAN Z L. Modeling of gas-solid multi-way coupling of fluidization of slender particles in riser [J]. CIESC Journal, 2015, 66(11): 4342-4350.

[8]古新, 朱培纳, 刘敏珊, 等. 变截面导流筒换热器入口流场均化性能数值仿真 [J]. 化工学报, 2012, 63(12): 3839-3846.DOI: 10.3969/j.issn.0438-1157.2012.12.015. GU X, ZHU P N, LIU M S, et al. Modeling of gas-solid multi-way coupling of fluidization of slender particles in riser [J]. CIESC Journal, 2012, 63(12): 3839-3846.

[9]李相鹏, 洪滔, 高增梁. 催化剂颗粒在弯道与渐扩管组合管系内的运动分布特征 [J]. 中南大学学报(自然科学版), 2012, 43(12): 4722-4728. LI X P, HONG T, Gao Z L. Motion and distribution of catalyst particles in pipe system combined with elbow and diverging tube [J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4722-4728.

[10]王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京:清华大学出版社, 2004: 221. WANG F J. Computational Fluid Dynamics Analysis: CFD Software Principles and Applications[M]. Beijing: Tsinghua University Press, 2004: 221.

[11]王慧, 黄咏梅. 不同形状涡街发生体流场仿真及特性研究 [J]. 中国计量学院学报, 2013, 24(3): 237-242. WANG H, HUANG Y M. Fluid simulation and characteristic investigation for different vortex shedders [J]. Journal of China University of Metrology, 2013, 24(3): 237- 242.

[12]张颉, 张泽, 胡永锋. 高浓度电除尘器入口封头气固两相流动的近流线数值模拟 [J]. 化工学报, 2004, 55(9): 1448-1454. ZHANG J, ZHANG Z, HU Y F, et al. Close-to-streamline numerical simulation of gas-solid flow in high concentration ESP gas inlet hood [J]. Journal of Chemical Industry and Engineering(China), 2004, 55(9): 1449-1454.

[13]TSAI R, HUANG J S. Combined effects of thermophoresis and electrophoresis on particle deposition onto a vertical flat plate from mixed convection flow through a porous medium [J]. Chemical Engineering Journal, 2010, 157(1): 52-59.

[14]CHEN C L, CHAN K C. Combined effects of thermophoresis andelectrophoresis on particle deposition onto a wavy surface disk [J]. International Journal of Heat & Mass Transfer, 2008, 51(11): 2657-2664.

[15]BOLOGA A, SEIFERT H, PAUR H R, et al. Collection of fine particles by novel wet electrostatic precipitator [J]. IEEE Transactions on Industry Applications, 2010, 45(6): 2170-2177.

[16]沈丹, 仲兆平, 过小玲. 600MW电厂SCR烟气脱硝反应器内不同导流板的流场数值模拟 [J]. 电力科技与环保, 2007, 23(1): 42-45. SHEN D, ZONG Z P, GUO X L. Numerical simulation of different guide plates in selective catalytic reduction denitrification reactor of 600MW power plant[J]. Electric Power Environmental Protection, 2007, 23(1): 42-45.

[17]俞逾, 杨晨, 范莉. 电厂SCR系统的设计与数值模拟 [J]. 现代电力, 2007, 24(3): 58-62. YU Y, YANG C, FAN L. Design and numerical simulation for selective catalytic reduction system in power plant[J]. Modern Electric Power, 2007, 24(3): 59-61.

[18]洪文鹏, 兰江. SCR脱硝系统静态混合器数值模拟 [J]. 锅炉技术, 2014, 45(3): 68-73. HONG W P, LAN J. Numerical simulation of static Mixer in static mixer in SCR denitrification system [J]. Boiler Technology, 2014, 45(3): 68-74.

[19]杨超, 张杰群, 郭婷婷. SCR烟气脱硝装置烟气流场数值模拟 [J].东北电力大学学报, 2012, 32(1): 66-70. YANG C, ZHANG J Q, GUO T T. Numerical simulation of the flow field in a SCR system [J]. Journal of Northeast Dianli University, 2012, 32(1): 66-70.

[20]JUN Y D, TABAKOFF W. Numerical simulation of a dilute particulate flow (laminar) over tube banks [J]. Journal of Fluids Engineering, 1994, 116(4): 770-777.

[21]JOFRÉ V P, ASSOF M V, FANZONE M L, et al. Optimization of ultrasound assisted-emulsification-dispersive liquid-liquid microextraction by experimental design methodologies for the determination of sulfur compounds in wines by gas chromatographymass spectrometry [J]. Analytica Chimica Acta, 2010, 683(1): 126-135.

[22]NEUBURGER M, ROTZINGER M, KAISER H. A simplex method for function minimization [J]. Computer Journal, 1965, 7(4): 308-313.

Motion and distribution of gas-solid two-phase flow in elbow with two-phase deflector

PAN Xiaohui, MA Chunyuan, CUI Lin
(National Engineering Laboratory for Coal-fired Pollutants Emission Reduction, Shandong University, Jinan 250061, Shandong, China)

Abstract:In view of the problem that gas-solid two-phase flow is not evenly distributed in the elbow of the entrance of flue gas pollutants removal system in the coal-fired power plant，a new two-phase deflector structure was put forward. CFD numerical simulation was employed to analyze the uniform effect of two-phase deflector and conventional deflector. The effect of the two-phase deflector on the distribution law of flow velocity and particle mass, and the effect of the plate shape and the plate angle on the uniform effect of two-phase deflector were simultaneously studied. Finally, the optimum structure of the two-phase deflector was obtained by the Design-Expert response surface method and CFD. The optimal structure was applied to the industrial test and the final result of the calculation and industrial test data were compared. The results showed that it is better to install two-phase deflector than deflector or delta wing baffle in the elbow because of the more uniform distribution and lower pressure drop. The flow velocity distribution and the particle mass concentration distribution changed gradually with the increase of the angle between the plates and the pressure drop of the elbow increased with theangle between the plates too. The optimum structure was the two-phase deflector with the angle of 75.49°and straight plate type. The comparison between the simulation and field measurements showed good agreement. The numerical simulation method proposed by this paper can be used to calculate gas-solid flows in the ESP inlet elbow with complex internal structure in detail.

Key words:two-phase flow; elbow; numerical simulation; homogenization; distribution

中图分类号：TQ 051.1

文献标志码：A

文章编号：0438—1157（2016）06—2308—10

DOI：10.11949/j.issn.0438-1157.20151633

基金项目：国家自然科学基金项目（51006063）；山东省自然科学基金项目(2014EEM040)；山东省自主创新基金项目（2014ZZCX05201）；山东大学基本科研业务费专项资金项目（2014QY001-04)。

Corresponding author:Prof. MA Chunyuan, sdetechym@163.com