回质回热吸附式制冷循环的热力学分析与方案优选
徐圣知,王丽伟,王如竹(上海交通大学制冷与低温工程研究所,上海 200240)
回质回热吸附式制冷循环的热力学分析与方案优选
徐圣知,王丽伟,王如竹
(上海交通大学制冷与低温工程研究所,上海 200240)
摘要:吸附式制冷是一种能利用低品位热能的节能环保的制冷方式。在空调工况下,硅胶-水回质回热系统应用最多。为了解在特定工况下选择何种循环能提升系统性能,应用热力学第一与第二定律评价指标分析了基本循环、回质循环、回质回热循环的COP、㶲效率、循环熵产。分析表明,回质循环存在推荐最高热源温度和最优热源温度,回质回热循环存在推荐最低热源温度和最优热源温度。例如对于典型夏季空调工况热源温度90℃、蒸发温度10℃、冷凝温度40℃,回质循环的推荐最高热源温度为93℃,高于实际热源温度90℃,选用回质循环更合适而非回质回热循环。最后,对制冷机组的分析表明给出的方法和推荐工作温度区间能针对实际系统给出方案优选和系统控制的指导性建议。
关键词:吸附式制冷;回质回热;热力学;熵;㶲
2015-11-30收到初稿,2016-03-07收到修改稿。
联系人:王如竹。第一作者:徐圣知(1992—),男,博士研究生。
Received date: 2015-11-30.
Foundation item: supported by the National Natural Science Foundation of China of Innovation Team (51521004).
引 言
20世纪以来,随着世界工业和经济的发展,能源危机和环境污染的问题日益严峻。这样的背景推动了一系列能源利用和环境保护技术的开发。吸附式制冷作为一种能够利用低品位热能并且环境友好的制冷技术,在世界上受到越来越多的关注[1]。
目前在设计和评价吸附式制冷系统时多采用热力学第一定律,例如能效比COP的分析[2-6],或者结合传热和试验分析系统的单位质量吸附剂制冷功率SCP[5-6]。为了从能量品位的角度分析吸附式制冷循环,应该引入热力学第二定律㶲和熵的分析。㶲的分析在吸附式制冷领域应用较少,主要用于吸附冷电联产系统[7-8],应用时主要考虑到功与热不在一个品位等级,为了更好地反映系统的总体性能而引入㶲效率的分析。熵的分析主要为针对具体系统计算熵产[9-10],也有针对工质对和循环进行熵产分析[11],但涵盖面不够广泛,也没有给出具体的针对方案优选和系统控制等方面的建议。
对于空调制冷工况,硅胶-水吸附式制冷系统受到更多关注,因为它能使用包括太阳能在内的低品位热能[12]。在硅胶-水吸附式制冷系统中,应用最多的是回质回热系统。例如Wang等[13]设计并测试的回质回热系统在热水温度84.8℃,冷却水温度30.6℃,冷冻水温度11.7℃时,制冷量和COP可分别达7.15 kW和0.38,已有较好的实用性能。Lu等[14]报道了回质回热对硅胶-水吸附式制冷空调性能的提升,例如当热水进口温度、冷却水进口温度、冷冻水出口温度分别为55、26、16℃时,回质COP可达0.31。当热水进口温度、冷却水进口温度、冷冻水出口温度分别为80、30、15℃时,回质COP可达0.5,回质回热COP可达0.53,接近回质COP。可见不同工况和循环下系统的性能有所不同,在某些工况下选择特定的循环能显著提高系统的性能。因此,在热力学评价指标的评判下,在何种工况下选择何种循环,又在何种工况下这些循环对能量的利用效果更好是本文研究的重点。
因吸附式制冷系统中不包含热功转换过程,故本文主要从循环分析的角度,选定硅胶-水基本循环、回质循环、回质回热循环为研究循环,选用更有参考价值的热力学第一、第二定律分析评价指标COP、㶲效率和循环熵产,对吸附式制冷循环进行较为全面的热力学分析,以提供方案优选的指导性建议,帮助选择合适的循环和工况,对现有吸附式制冷系统进行热力学评价,给出系统控制的指导性建议。
1 选定吸附式制冷循环的数学建模
1.1基本循环
对于物理吸附,基本吸附式制冷循环的Clapeyron图如图1所示[15]。
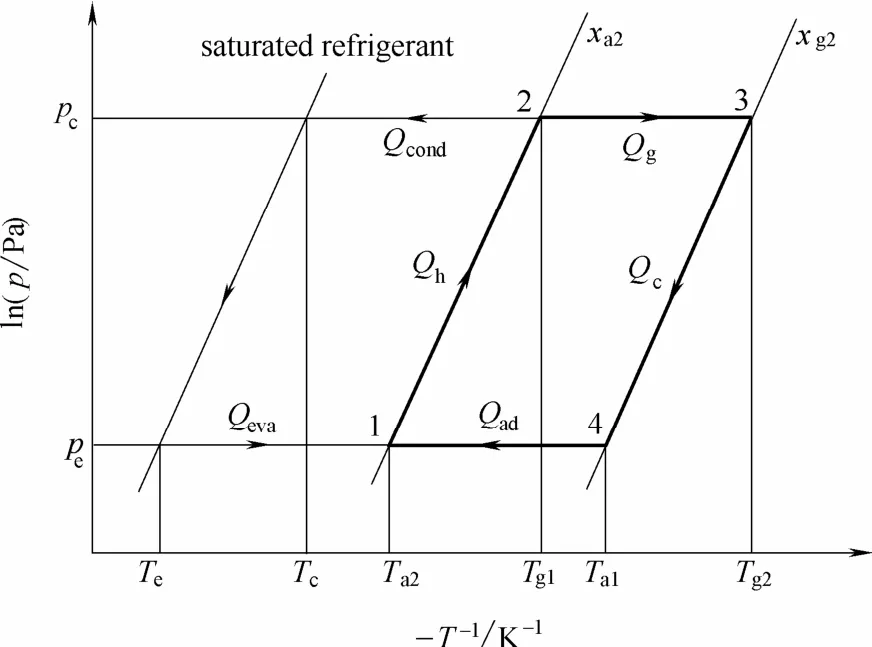
图1 基本物理吸附式制冷循环Clapeyron图Fig.1 Clapeyron diagram of basic physical adsorption refrigeration cycle
物理吸附的平衡吸附率可通过Dubinin-Astakhov(D-A)方程的简化形式[16-17]计算得到
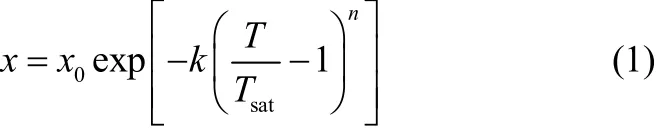
式中,x为平衡吸附率,kg·kg−1;T为吸附床温度,K;Tsat为制冷剂饱和温度,K;x0、k、n为方程参数,对于硅胶-水工质对,x0=0.346 kg·kg−1,k=5.6,n=1.6[18]。
基本物理吸附式制冷循环的循环吸附量为

式中,xa2为吸附终了吸附率,kg·kg−1;xg2为解吸终了吸附率,kg·kg−1。
文献[15]中,加热过程(图1中过程1-2)吸附床吸收的热量为
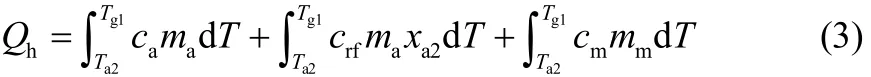
式中,ca为吸附剂的比热容,J·kg−1·K−1;ma为吸附剂的质量,kg;crf为制冷剂液体的比热容,J·kg−1·K−1;cm为吸附床金属的比热容,J·kg−1·K−1;mm为吸附床金属的质量,kg;T为吸附床温度,K;Tg1为解吸开始温度,K。
解吸过程(图1中过程2-3)吸附床吸收的热量为
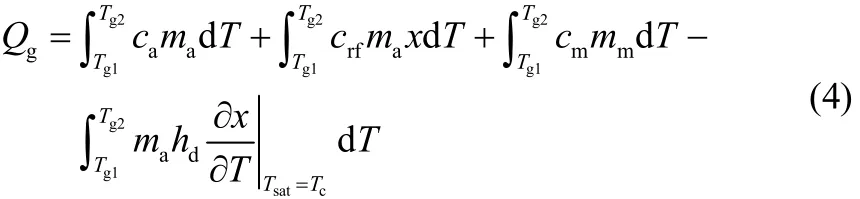
式中,hd为单位质量制冷剂的解吸热,J·kg−1。
冷却过程(图1中过程3-4)吸附床放出的热量为
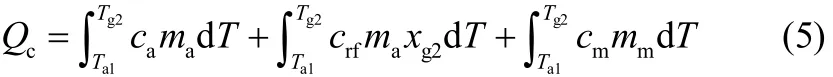
式中,Ta1为吸附开始温度,K。
吸附过程(图1中过程4-1)吸附床放出的热量为
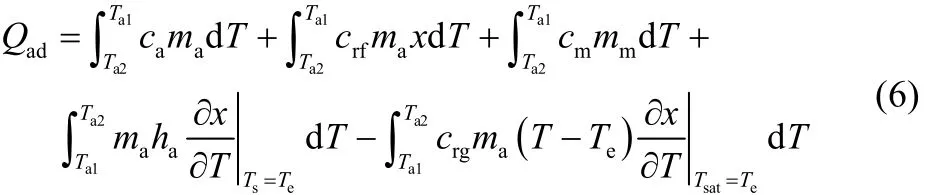
式中,ha为单位质量制冷剂的吸附热,J·kg−1;crg为制冷剂气体的比定压热容,J·kg−1·K−1。
适用于物理吸附的Clausius-Clapeyron方程为[15]
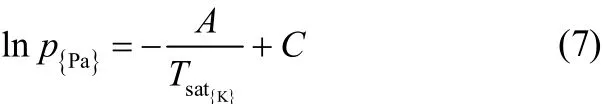
式中,p为制冷剂压强;Tsat为制冷剂饱和温度;A、C为方程参数。
单位质量制冷剂在冷凝压强下解吸时的解吸热和蒸发压强下吸附时的吸附热分别为
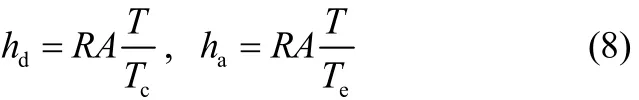
式中,R为制冷剂的理想气体常数,J·kg−1·K−1;A为式(7)的参数,K;T为吸附床温度,K。
基本物理吸附式制冷循环的循环制冷量为
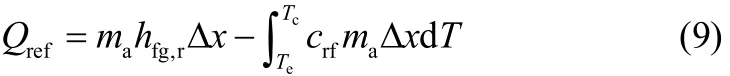
式中,hfg,r为单位质量制冷剂在蒸发温度下的汽化潜热,J·kg−1。
基本物理吸附式制冷循环的COP为

忽略传热温差,基本物理吸附式制冷循环的㶲效率可定义为冷量㶲比热量㶲
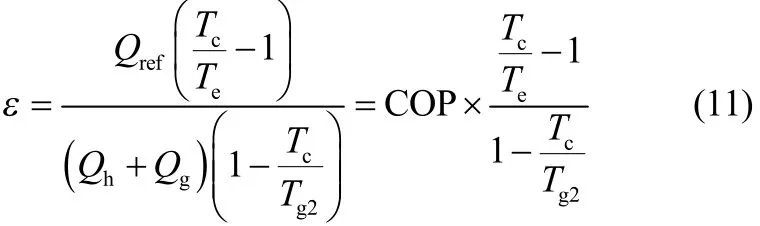
关于循环熵产,在一个制冷循环之后,系统的熵变为0,则熵产是熵流的相反数。对于基本物理吸附式制冷循环,单位质量吸附剂对应的循环熵产(J·kg−1·K−1)为
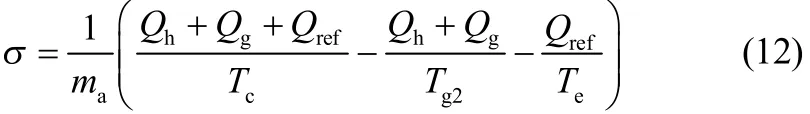
1.2回质循环
回质循环是质驱动的优化循环,利用吸附床解吸完成和吸附完成时的压差,将两个压强不同的吸附床连通,这样可以促进压强较高的吸附床进一步解吸,压强较低的吸附床吸附这部分解吸的制冷剂,从而增加了循环吸附量和循环制冷量。对于物理吸附,回质循环的Clapeyron图如图2所示[15,19]。
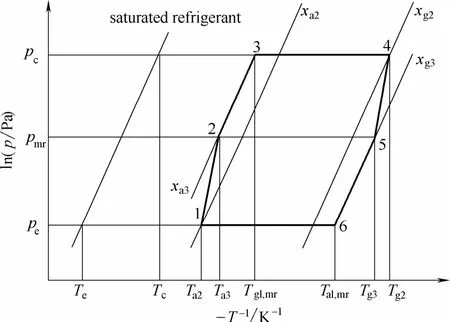
图2 回质物理吸附式制冷循环Clapeyron图Fig.2 Clapeyron diagram of mass recovery physical adsorption refrigeration cycle
图2中1-2和4-5的过程分别是压强较低的吸附床和压强较高的吸附床的回质过程。回质后两个吸附床的压强均为回质压强pmr。对比图1可以看出,回质循环的循环吸附量xa2−xg3高于相同工况下基本循环的循环吸附量xa2−xg2。在分析回质循环时可以只考虑单吸附床,不会对结果产生影响。
对于回质物理吸附式制冷循环,存在吸附率关系

式中,xa3为吸附回质吸附率,即压强较低的吸附床回质后的吸附率,kg·kg−1;xg3为解吸回质吸附率,即压强较高的吸附床回质后的吸附率,kg·kg−1。
回质过程为两个吸附床各自的绝热过程,则高温吸附床的解吸热会导致高温床的温度降低,有
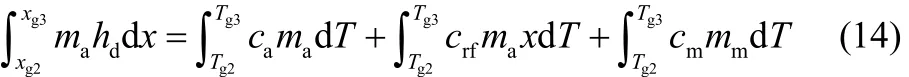
式中,Tg3为解吸回质温度,即压强较高的吸附床回质后的温度,K。
低温吸附床的吸附热及高温吸附床解吸出的高温气态制冷剂的显热会导致低温床的温度上升,有
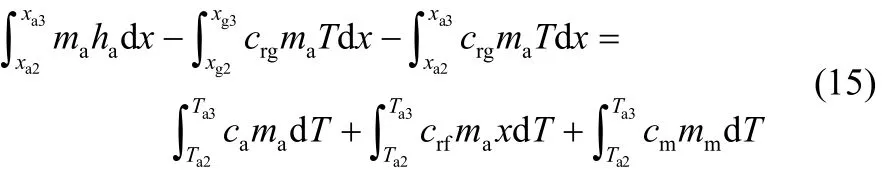
加热过程(图2中过程2-3)吸附床吸收的热量为
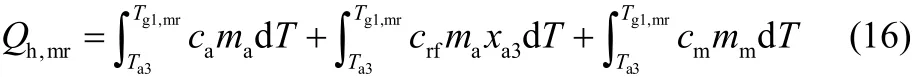
解吸过程(图2中过程3-4)吸附床吸收的热量为
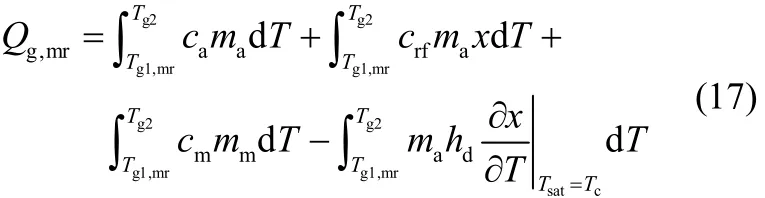
类似于基本循环,回质物理吸附式制冷循环的COP为
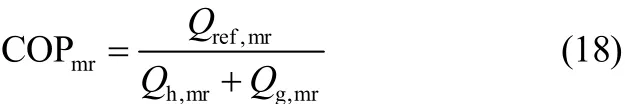
回质物理吸附式制冷循环的㶲效率为
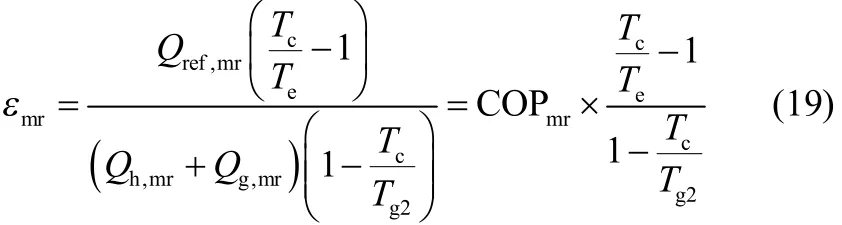
对于回质物理吸附式制冷循环,每千克吸附剂对应的循环熵产为
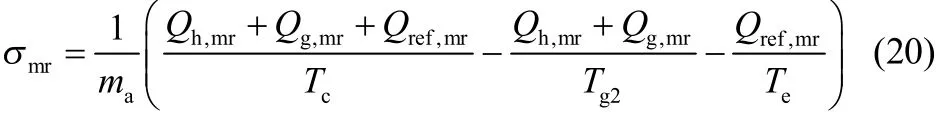
除了普通的回质过程,还有一种类回质过程。类回质过程,即对两个吸附床对应的蒸发器和冷凝器进行回热,而并非直接将两个吸附床连通使两个吸附床之间有制冷剂的物质交换,这样就不需要在两个吸附床之间设置阀门,一定程度上增加了系统的可靠性[20]。
1.3回质回热循环
尽管回质循环利用吸附床解吸完成和吸附完成时的压强差增加了循环吸附量,回质后的两个吸附床仍然一个温度较高需要冷却,另一个温度较低需要加热。回质回热循环即在回质循环的基础上利用高温吸附床回质后冷却时多余的热量加热低温吸附床,以减少系统对外界热源输入热量的需求。对于物理吸附,回质回热循环的Clapeyron图如图3所示[15,19]。
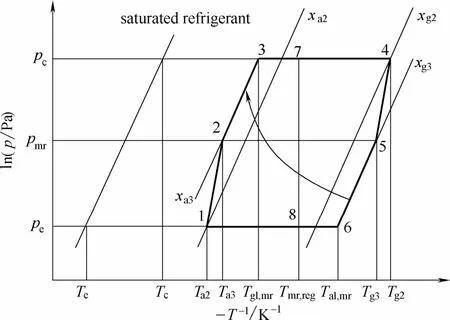
图3 回质回热物理吸附式制冷循环Clapeyron图Fig.3 Clapeyron diagram of mass and heat recovery physical adsorption refrigeration cycle
图3中相应的状态点与回质吸附式制冷循环(图2)相同。区别在于图3中2-3-7过程所需的加热量由5-6-8过程放出的热量提供。状态7、8对应回质回热温度Tmr,reg,保证回热过程的热量从高温向低温传递。与回质循环类似,在分析回质回热循环时可以只考虑单吸附床,不会对结果产生影响。
在回热过程中,高温吸附床放出的热量等于低温吸附床吸收的热量,即

回质回热物理吸附式制冷循环的COP为回质回热物理吸附式制冷循环的㶲效率为
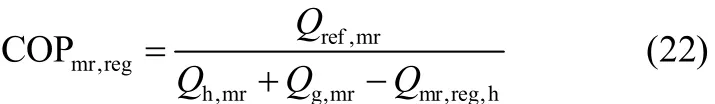
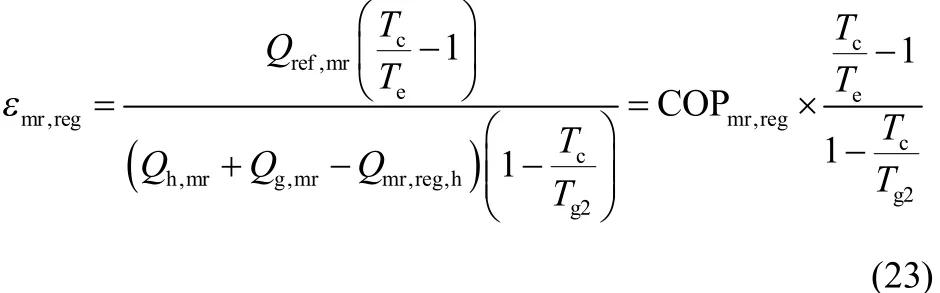
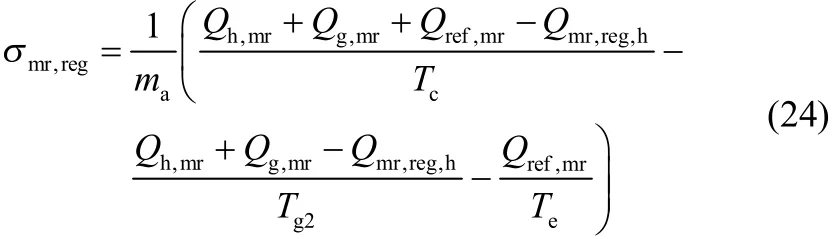
对于回质回热物理吸附式制冷循环,每千克吸附剂对应的循环熵产为
2 吸附式制冷循环的热力学分析
2.1吸附床金属比热容与非平衡吸附考虑
考虑到不同的设计方案吸附床的金属比热容也不同,为了得到一个普适的结果,在计算中忽略了吸附床的金属比热容。同样地,为了在计算时不需要引入具体系统参数和循环时间等变量,在计算时只考虑了平衡吸附率,没有引入非平衡吸附计算模型。因此实际系统的热力学评价指标会有一定的变化。但是,因为在计算过程中已经充分考虑了平衡吸附与解吸的热动力学,所以给出的结论仍然基本适用。这样,本文给出的结果就可以作为吸附式制冷系统设计和优化的参考,在进行详细的系统设计前给出方案优选和系统控制的指导性建议,确定优选的循环和工况。
2.2基本循环、回质循环与回质回热循环
以空调工况为例,考虑硅胶-水工质对,分别计算基本循环、回质循环、回质回热循环在冷凝温度20~40℃、蒸发温度1~20℃、热源温度50~120℃工况下的COP、㶲效率、循环熵产,部分结果如图4~图6所示。
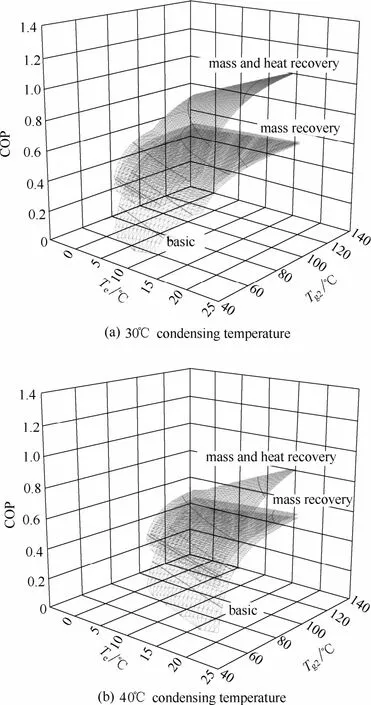
图4 基本循环、回质循环、回质回热循环的COPFig.4 COP of basic cycle, mass recovery cycle, and mass and heat recovery cycle
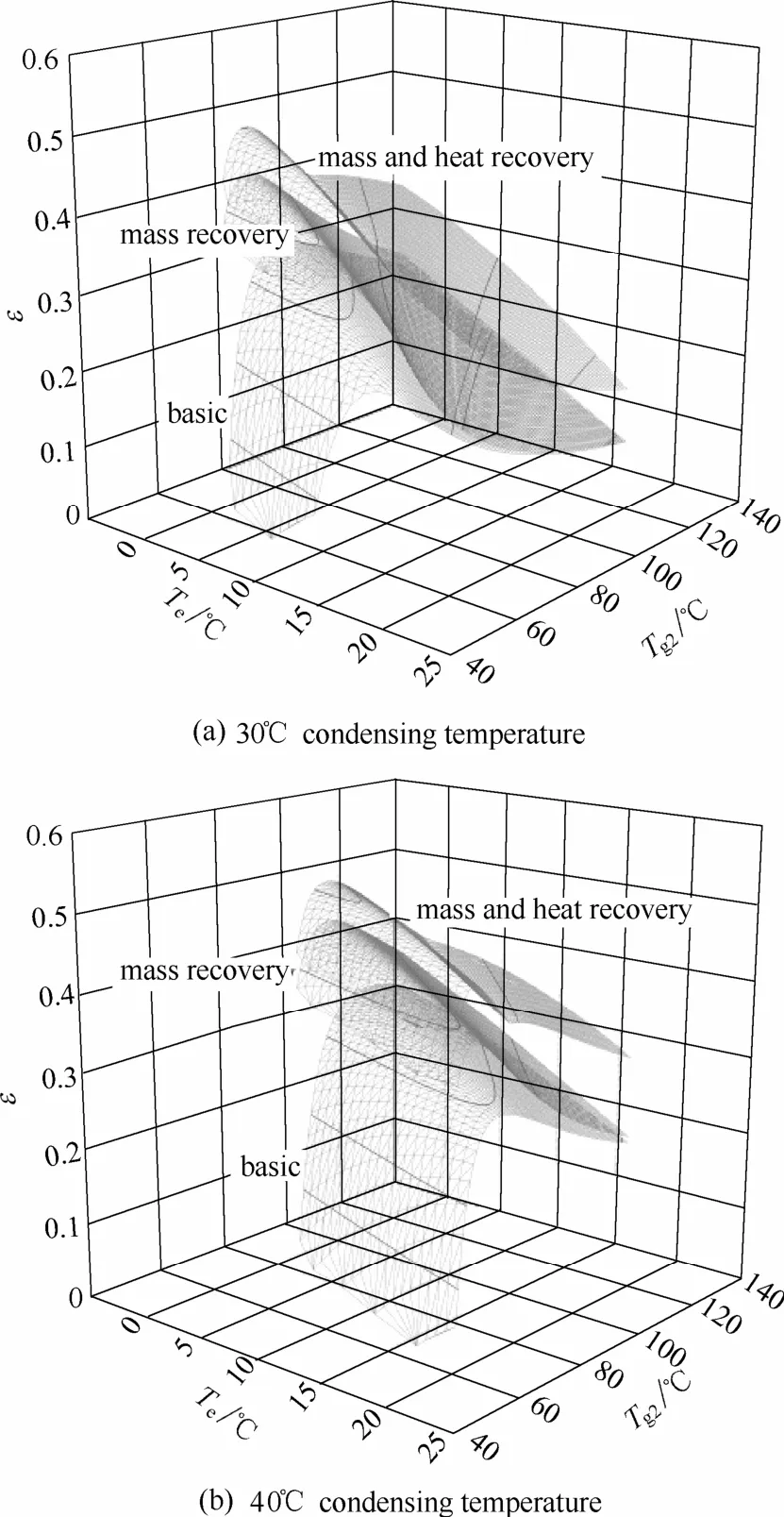
图5 基本循环、回质循环、回质回热循环的㶲效率Fig.5 Exergetic efficiency of basic cycle, mass recovery cycle, and mass and heat recovery cycle
从图4可以看出,在相同工况下,回质循环的COP均高于基本循环,回质回热循环的COP均高于回质循环。仅在热源温度较低时回质循环的COP相较于基本循环有显著提升,而回质回热循环仅在热源温度较高时COP相较于回质循环有显著提升。例如当冷凝温度为30℃、蒸发温度为5℃、热源温度为60℃时,基本循环的COP为0.174,回质循环的COP为0.410,相较于基本循环提升136%,回质回热循环的COP为0.472,相较于回质循环仅提升15%。当热源温度升高到100℃、其他工况不变时,基本循环的COP为0.563,回质循环的COP为0.604,相较于基本循环仅提升7%,回质回热循环的COP为0.802,相较于回质循环提升33%。考虑到实际系统中增加回质和回热过程可能产生的能量浪费,可以取20%作为判断标准,即当回质循环的COP超过基本循环20%时,推荐采用回质循环,当回质回热循环的COP超过回质循环20%时,推荐采用回质回热循环。这样就可以确定回质循环的推荐最高热源温度和回质回热循环的推荐最低热源温度。这个比例可根据实际需要选取。
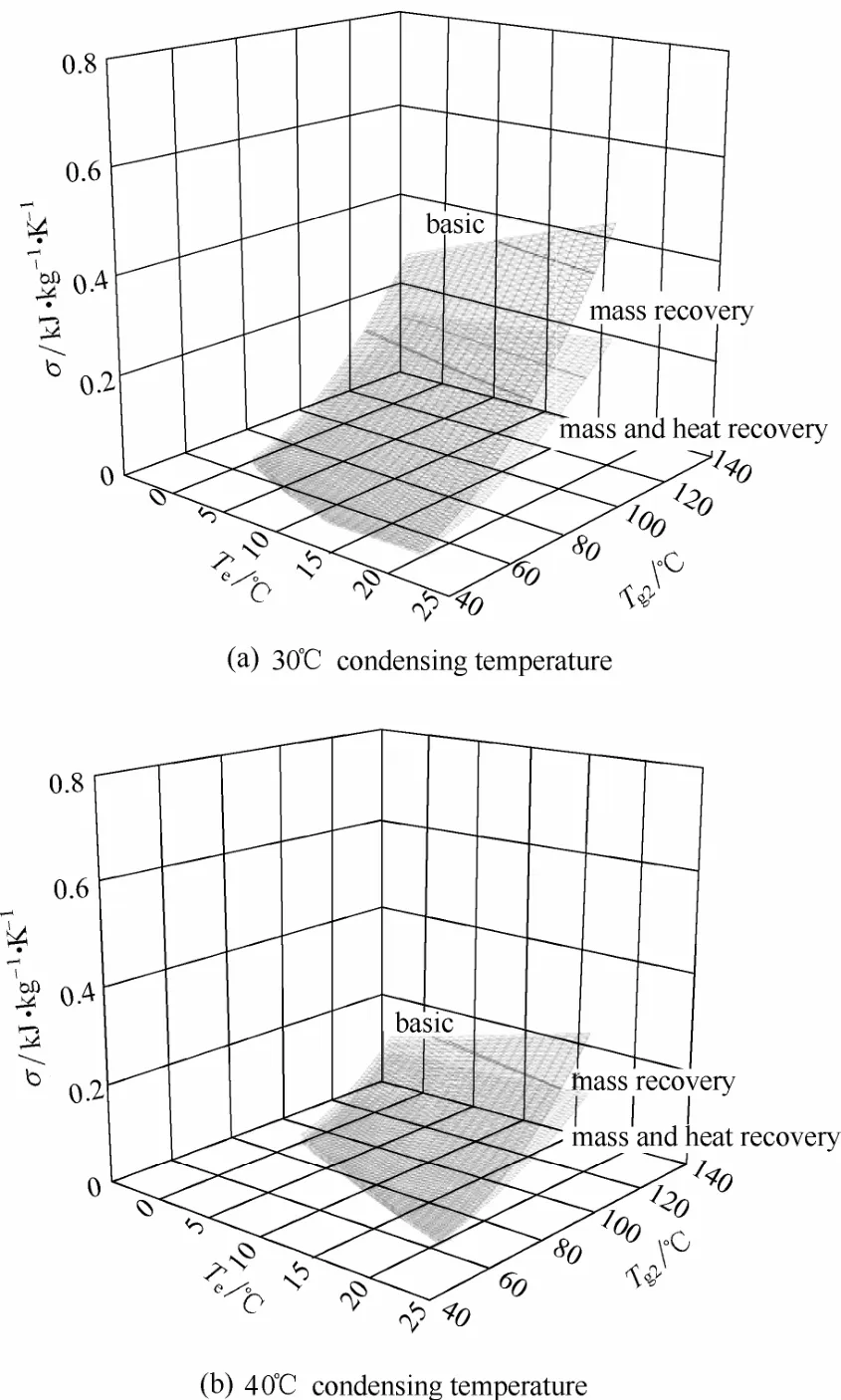
图6 基本循环、回质循环、回质回热循环的循环熵产Fig.6 Cycle entropy production of basic cycle, mass recovery cycle, and mass and heat recovery cycle
从图5可以看出,回质循环与回质回热循环的㶲效率均随着热源温度的升高先上升后下降。因此,回质循环与回质回热循环均存在关于㶲效率的最优热源温度,且两种循环的最优热源温度基本相同。例如当冷凝温度为40℃、蒸发温度为10℃时,回质循环的最大㶲效率为0.432,对应的热源温度为81℃,回质回热循环的最大㶲效率为0.491,对应的热源温度也为81℃。
从图6可以看出,回质循环的循环熵产与基本循环基本相同,而回质回热循环的循环熵产明显低于回质循环和基本循环。例如当冷凝温度为30℃、蒸发温度为5℃、热源温度为100℃时,基本循环的循环熵产为0.201 kJ·kg−1·K−1,回质循环的循环熵产为0.195 kJ·kg−1·K−1,回质回热循环的循环熵产为0.128 kJ·kg−1·K−1。由此可以认为,吸附式制冷系统内部的传质过程如回质过程并不会显著影响循环熵产,增加内部换热过程则能降低系统对外部热源输入热量的需求,从而显著降低循环熵产。
因此,在热力学评价指标的评判下,理论上回质回热循环始终优于回质循环,而回质循环始终优于基本循环。但根据COP与㶲效率的分析和实际系统的考虑,回质循环有最优热源温度和推荐最高热源温度,回质回热循环有推荐最低热源温度和最优热源温度,加上驱动回质循环的最低热源温度和硅胶允许的最高工作温度的限制,可以给出回质循环与回质回热循环的推荐工作温度区间指导表格。
表1列出了回质循环的最低热源温度、最优热源温度、推荐最高热源温度。
表1中工质对为硅胶-水;Th,min代表驱动回质循环的最低热源温度;Th,opt代表回质循环的最优热源温度;Th,max代表回质循环的推荐最高热源温度;“/”代表无推荐最高热源温度且在该工况下不推荐选用回质循环;仅考虑了热源温度大于等于50℃的情况。
从表1可以看出,回质循环的最优热源温度总在最低热源温度与推荐最高热源温度之间。例如当冷凝温度为30℃、蒸发温度为7℃时,驱动回质循环的最低热源温度为55℃,推荐最高热源温度为71℃,表示热源温度在这个范围内时,可以选用回质循环以获得比基本循环更高的COP。在这个温区中,如果热源温度接近于61℃,系统将获得最优的能量品位利用效果,即最高的㶲效率。当冷凝温度为20℃、蒸发温度为5℃以上时,回质循环的COP相较于基本循环提升不高,考虑到引入实际回质过程相比理论情况会有一定的性能下降,这时不推荐选用回质循环,可以只采用基本循环,可能会获得更好的性能。
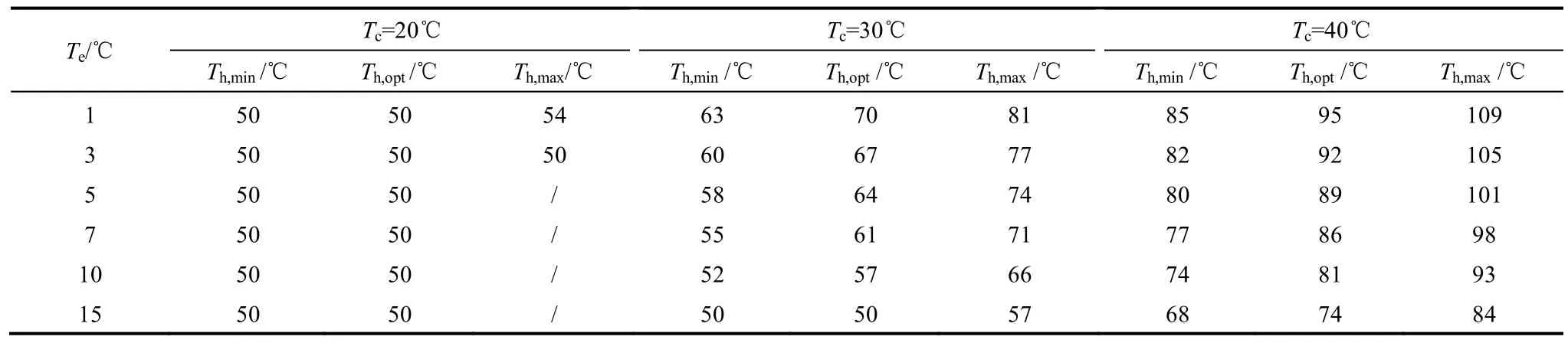
表1 回质循环的最低热源温度、最优热源温度、推荐最高热源温度Table 1 Lowest, optimum and recommended highest heating source temperature of mass recovery cycle
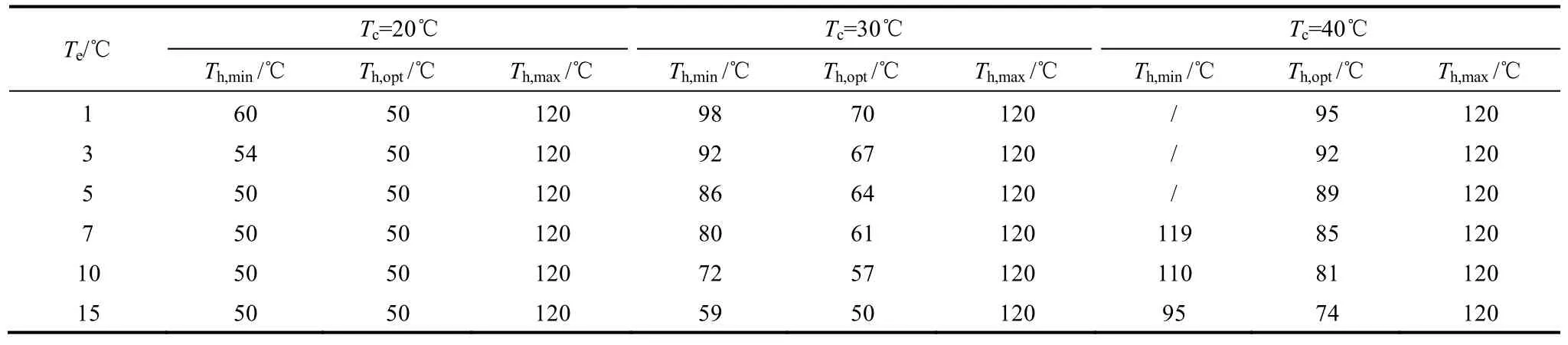
表2 回质回热循环的推荐最低热源温度、最优热源温度、最高热源温度Table 2 Recommended lowest, optimum and highest heating source temperature of mass and heat recovery cycle
表2列出了回质回热循环的推荐最低热源温度、最优热源温度、最高热源温度。
表2中工质对为硅胶-水;Th,min代表回质回热循环的推荐最低热源温度;Th,opt代表回质回热循环的最优热源温度;Th,max代表回质回热循环允许的最高热源温度;“/”代表无推荐最低热源温度且在该工况下不推荐选用回质回热循环;仅考虑了热源温度大于等于50℃且小于等于120℃的情况。
从表2可以看出,回质回热循环的最优热源温度不在推荐最低热源温度与最高热源温度之间,这是因为回质回热循环在热源温度较高时的COP提升效果更好,而在这个温区㶲效率已经开始显著下降。例如当冷凝温度为30℃、蒸发温度为7℃时,回质回热循环的推荐最低热源温度为80℃,允许的最高热源温度为120℃,表示热源温度在这个范围内时,可以选用回质回热循环以获得比回质循环更高的COP。但如果热源温度接近于61℃,系统将获得最优的能量品位利用效果,即最高的㶲效率。这时就需要根据热源的情况进行权衡。当冷凝温度为40℃,蒸发温度低于5℃时,回质回热循环相较于回质循环的性能提升不显著,这时应一并参考表1确定优选循环,如果符合回质循环的推荐工作温度区间,应选择回质循环。如果选定的工况同时在回质循环与回质回热循环的推荐温区之外,例如当冷凝温度为30℃、蒸发温度为7℃、热源温度在72~79℃之间时,应考虑选择基本循环。
2.3实际系统的热力学评价
根据对如图7所示的一台硅胶-水类回质回热吸附式制冷机组的分析测试[21],将文献[21]中的试验数据与本文的模拟计算结果相比较,可以得到表3。
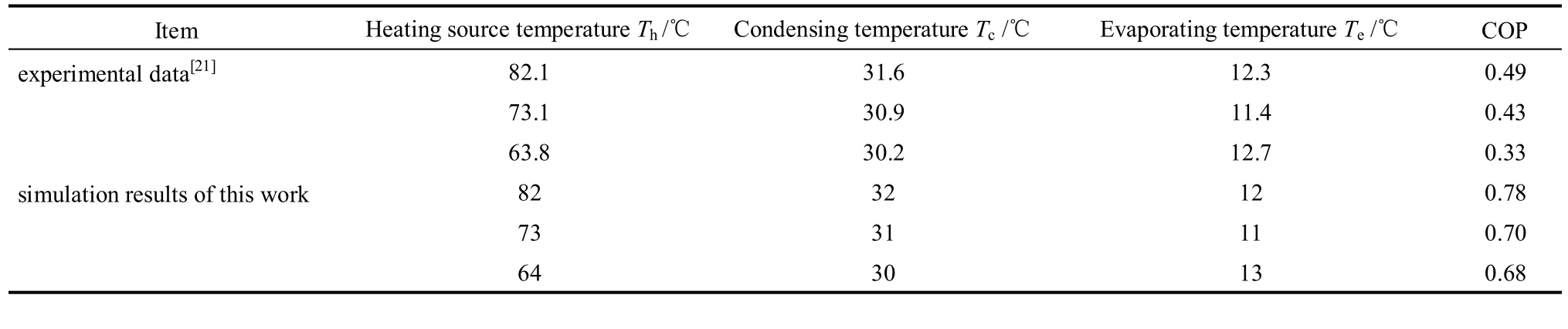
表3 试验数据与模拟计算结果比较Table 3 Comparison of experimental data and simulation results

图7 硅胶-水类回质回热吸附式制冷机组Fig.7 Silica gel-water mass recovery-like and heat recovery adsorption chiller
从表3可以看出,因为本文在模拟计算时充分考虑了平衡吸附与解吸的热动力学,所以本文计算结果的趋势与文献[21]一致。然而,因为在计算时忽略了非平衡吸附以及吸附床金属比热容的影响,前两组计算数据的COP均比文献[21]中的试验结果高出约60%。值得注意的是,第3组计算数据的COP与试验数据相差很大,高出了106%。
参照表2可以发现其原因:对于第3组数据的工况,近似取冷凝温度为30℃,蒸发温度在10~15℃之间,这时回质回热循环的推荐最低热源温度在59~72℃之间,中间值为65.5℃,高于试验时的热水进口温度63.8℃。按照本文中的结论,热源温度在推荐最低热源温度以下时,回质回热循环相对于回质循环的性能提升效果不明显,又因为引入实际回质回热过程会产生一定的能量浪费,这时回质回热循环的表现可能反而不如回质循环或基本循环。因此表现为本文中的模拟计算结果显著高于试验数据。
参照表1可以发现,这一组数据的热源温度也高于回质循环的推荐最高热源温度,因此在这个工况下回质循环相对于基本循环的性能提升也不显著,可以考虑在这个工况下控制机组阀门切换为基本循环或回热循环工作模式,可能会获得更好的性能。
3 结 论
(1)考虑到循环的实际工作能效比,热力学第一定律评价指标COP应是循环优选的首选参考指标,其次应在许可范围内考虑热力学第二定律评价指标㶲效率的提升,优化循环对能量品位的利用效果。相比之下,循环熵产仅能反映循环的热驱动优化效果如回热,不能反映质驱动优化如回质,因此不太适合用于包含回质的吸附式制冷循环与工况的选择优化。
(2)认为回质循环存在最优热源温度和推荐最高热源温度,如表1所列。例如当冷凝温度为40℃、蒸发温度为5℃时,硅胶-水回质循环的最低热源温度为80℃,最优热源温度为89℃,推荐最高热源温度为101℃。类似地,认为回质回热循环存在推荐最低热源温度和最优热源温度,如表2所列。
(3)对硅胶-水类回质回热吸附式制冷机组的分析表明,虽然本文中的模拟计算忽略了非平衡吸附和吸附床金属比热容的影响使得结果与实际系统的COP有一定的偏差,但本文给出的方法和推荐工作温度区间能够针对实际系统给出方案优选和系统控制的指导性建议。
符号说明
A——Clausius-Clapeyron方程参数,K
C——Clausius-Clapeyron方程参数
COP——能效比
c——比热容,J·kg−1·K−1
ha——单位质量制冷剂的吸附热,J·kg−1
hd——单位质量制冷剂的解吸热,J·kg−1
hfg,r——单位质量制冷剂的汽化潜热,J·kg−1
k——D-A方程参数
m——质量,kg
n——D-A方程参数
p——压强,Pa
R——制冷剂的理想气体常数,J·kg−1·K−1
Q——热量,J
T——温度、吸附床温度,K
x——平衡吸附率,kg·kg−1
x0——D-A方程参数,kg·kg−1
Δx——循环吸附量,kg·kg−1
ε——㶲效率
σ——单位质量吸附剂对应的循环熵产,J·kg−1·K−1
下角标
a, ad——吸附、吸附剂、吸附床
c, cond——冷凝、冷却
e, eva——蒸发
g——解吸
h——加热,热源
m——金属
max——最大值
min——最小值
mr——回质
opt——最优值
ref——制冷
reg——回热
rf——制冷剂液体
rg——制冷剂气体
sat——饱和
References
[1]王如竹. 吸附式制冷新技术[J]. 化工学报, 2000, 51(4): 435-442. WANG R Z. Adsorption refrigeration: a new refrigeration technology [J]. Journal of Chemical Industry and Engineering (China), 2000, 51(4): 435-442.
[2]刘艳玲, 王如竹, 夏再忠. 一种新型太阳能吸附式制冷系统的设计及性能模拟[J]. 化工学报, 2005, 56(5): 791-795. LIU Y L, WANG R Z, XIA Z Z. Design and performance simulation of continuous solar powered adsorption air conditioning system [J]. Journal of Chemical Industry and Engineering (China), 2005, 56(5): 791-795.
[3]杨培志, 陈焕新. 吸附式制冷循环热力学及性能[J]. 中南大学学报(自然科学版), 2007, 38(3): 461-467. YANG P Z, CHEN H X. Thermodynamic analysis and performance of adsorption refrigeration loop [J]. Journal of Central South University (Science and Technology), 2007, 38(3): 461-467.
[4]孔祥强, 王如竹, 李瑛. 硅胶-水吸附式制冷机组变热源下制冷性能[J]. 农业机械学报, 2009, 40(9): 127-130, 160. KONG X Q, WANG R Z, LI Y. Refrigeration performance of a silica gel-water adsorption chiller driven by variable heat source [J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(9): 127-130, 160.
[5]胡远扬, 王健, 蔡浩仁, 等. 低温热源驱动的二级吸附冷冻循环实验研究与性能分析[J]. 制冷学报, 2010, 31(6): 6-11. HU Y Y, WANG J, CAI H R, et al. Experimental study and performance analysis on a two-stage adsorption freezing cycle driven by low-temperature heat source [J]. Journal of Refrigeration, 2010, 31(6): 6-11.
[6]罗伟莉, 王健, 王丽伟, 等. 采用SrCl2-NH4Cl-NH3工质对的二级吸附式冷冻循环性能[J]. 化工学报, 2012, 63(4): 1004-1010. LUO W L, WANG J, WANG L W, et al. Performance of two-stage adsorption freezing cycle with SrCl2-NH4CI-NH3[J]. CIESC Journal, 2012, 63(4): 1004-1010.
[7]WANG L W, ZIEGLER F, ROSKILLY A P, et al. A resorption cycle for the cogeneration of electricity and refrigeration [J]. Applied Energy, 2013, 106: 56-64.
[8]BAO H S, WANG Y D, ROSKILLY A P. Modelling of a chemisorption refrigeration and power cogeneration system [J]. Applied Energy, 2014, 119: 351-362.
[9]CHUA H T, NG K C, MALEK A, et al. Entropy generation analysis of two-bed, silica gel-water, non-regenerative adsorption chillers [J]. Journal of Physics D: Applied Physics, 1998, 31(12): 1471-1477.
[10]THU K, KIM Y D, MYAT A, et al. Entropy generation analysis of an adsorption cooling cycle [J]. International Journal of Heat and Mass Transfer, 2013, 60: 143-155.
[11]MEUNIER F, KAUSHIK S C, NEVEU P, et al. A comparative thermodynamic study of sorption systems: second law analysis [J]. International Journal of Refrigeration, 1996, 19(6): 414-421.
[12]WANG D C, XIA Z Z, WU J Y, et al. Study of a novel silica gel-water adsorption chiller (Ⅰ): Design and performance prediction [J]. International Journal of Refrigeration, 2005, 28(7): 1073-1083.
[13]WANG D C, WU J Y, XIA Z Z, et al. Study of a novel silica gel-water adsorption chiller (Ⅱ): Experimental study [J]. International Journal of Refrigeration, 2005, 28(7): 1084-1091.
[14]LU Z S, WANG R Z. Performance improvement by mass-heat recovery of an innovative adsorption air-conditioner driven by 50–80℃ hot water [J]. Applied Thermal Engineering, 2013, 55(1/2): 113-120.
[15]王如竹, 王丽伟, 吴静怡. 吸附式制冷理论与应用[M]. 北京: 科学出版社, 2007. WANG R Z, WANG L W, WU J Y. Theory and Application of Adsorption Refrigeration [M]. Beijing: Science Press, 2007.
[16]CRITOPH R E. Performance limitations of adsorption cycles for solar cooling [J]. Solar Energy, 1988, 41(1): 21-31.
[17]TAMAINOT-TELTO Z, CRITOPH R E. Adsorption refrigerator using monolithic carbon-ammonia pair [J]. International Journal of Refrigeration, 1997, 20(2): 146-155.
[18]DI J, WU J Y, XIA Z Z, et al. Theoretical and experimental study on characteristics of a novel silica gel-water chiller under the conditions of variable heat source temperature [J]. International Journal of Refrigeration, 2007, 30(3): 515-526.
[19]WANG R Z. Adsorption refrigeration research in Shanghai Jiao Tong University [J]. Renewable and Sustainable Energy Reviews, 2001, 5(1): 1-37.
[20]陈传涓, 夏再忠, 王如竹. 基于分布参数模型的硅胶-水制冷机的研究[J]. 工程热物理学报, 2009, 30(8): 1363-1365. CHEN C J, XIA Z Z, WANG R Z. Numerical simulation of a silica gel-water adsorption chiller based on a transient distributed-parameter model [J]. Journal of Engineering Thermophysics, 2009, 30(8): 1363-1365.
[21]陈传涓. 硅胶-水吸附式制冷系统的热设计方法研究[D]. 上海: 上海交通大学, 2010. CHEN C J. Study on the thermal design method for silica gel-water adsorption chillers [D]. Shanghai: Shanghai Jiao Tong University, 2010.
Thermodynamic analysis of mass and heat recovery adsorption refrigeration cycles and scheme selection
XU Shengzhi, WANG Liwei, WANG Ruzhu
(Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract:Adsorption refrigeration is an energy-saving and environmental-friendly refrigerating method, which can utilize low-grade thermal energy. Under air-conditioning working conditions, silica gel-water mass and heat recovery systems are most often used. In order to understand which kind of cycle can improve the performance of the system under specific working conditions, the evaluating indicators of the first and the second laws of thermodynamics were adopted to analyze the COP, the exergetic efficiency and the cycle entropy production of the basic cycle, mass recovery cycle and mass and heat recovery cycle. The analysis showed that only when the heating source temperature was relatively low, the COP of mass recovery cycle was remarkably higher than that of basic cycle. The COP of mass and heat recovery cycle was significantly higher than that of mass recovery cycle only when the heating source temperature was relatively high. Consequently, the mass recovery cycle had its recommended highest heating source temperature and optimum heating source temperature, while the mass and heat recovery cycle had its recommended lowest heating source temperature and optimum heating source temperature. For example, under the typical air-conditioning working condition in summer of 90℃ heating source temperature, 10℃ evaporating temperature and 40℃ condensing temperature, the recommended highest heating source temperature of mass recovery cycle was 93℃, which is higher than the heating source temperature of 90℃. As a result, the mass recovery cycle was more suitable under this working condition and should be chosen rather than the mass and heat recovery cycle. Finally, the analysis of a chiller indicated that the given method andrecommended working temperature intervals could provide guidance or advice on the scheme selection and system control for real systems.
Key words:adsorption refrigeration; mass and heat recovery; thermodynamics; entropy; exergy
中图分类号:TB 61+1
文献标志码:A
文章编号:0438—1157(2016)06—2202—09
DOI:10.11949/j.issn.0438-1157.20151803
基金项目:国家自然科学基金创新研究群体项目(51521004)。
Corresponding author:Prof. WANG Ruzhu, rzwang@sjtu.edu.cn

