竖直平板间液桥形状的观测与预测模型开发
庄大伟,杨艺菲,胡海涛,丁国良(上海交通大学制冷与低温工程研究所,上海 200240)
竖直平板间液桥形状的观测与预测模型开发
庄大伟,杨艺菲,胡海涛,丁国良
(上海交通大学制冷与低温工程研究所,上海 200240)
摘要:了解析湿工况下液桥对管翅式换热器性能的影响,需要对液桥形状进行实验研究并建立描述液桥形状的方法。通过搭建可视化实验台观察了液桥在竖直平板间的形状,并测量了液桥的接触线和接触角。实验研究了不同体积、不同平板间距、不同平板材料间形成的液桥,并通过实验数据开发了能够描述液桥形状的关联式,包括接触线伸长比和接触角分别与Bond数的关联式。还根据关联式建立了描述液桥形状的方法并将结果与实验数据进行对比,对比结果显示接触线的描述方法平均误差为3.4%,接触角的描述方法平均误差为7.9%。
关键词:液桥形状;接触角;预测;模型;实验验证
2015-11-11收到初稿,2016-02-16收到修改稿。
联系人:丁国良。第一作者:庄大伟(1987—),男,博士后。
Received date: 2015-11-11.
Foundation item: supported by the National Natural Science Foundation of China (51576122) and the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (51521004).
引 言
空调蒸发器的空气侧运行在湿工况下[1-3],使得湿空气中的水蒸气会在翅片表面冷凝形成液滴[4-6];液滴会随着冷凝过程不断长大[7-9],并不断与相邻翅片上的液滴发生接触并连接形成大量的液桥[10]。这些液桥若不能及时排出翅片,就会堵塞换热器空气侧流道、占用翅片换热面积,从而严重影响换热器的性能[8, 11-13]。要提高湿工况下换热器性能,就需要使形成的液桥能够快速排出换热器。为了能够使液桥快速排出,就需要对液桥的形状进行了解,并建立描述液桥形状的方法。
液桥形状包括液桥-翅片界面形状和液桥-湿空气界面形状,可通过液桥三相接触线和接触角来描述[14]:① 液桥-翅片界面是由三相接触线围成的平面;② 液桥-湿空气界面是以接触角为斜率的曲线绕接触线一周围成的曲面。因此要实现液桥形状的描述,就必须开发液桥三相接触线和接触角的定量预测模型。
液桥三相接触线和接触角模型的开发需要能够反映液桥所受表面张力、重力这两个因素的耦合影响。针对接触线和接触角的现有研究主要针对受到表面张力和轴向重力作用下的液桥,研究包括实验[14-17]和数值模型[18-21]两类。
已有实验研究包括对液桥轮廓的研究[14-16]和对接触线和接触角的测量[17]。Verges等[14]通过实验研究了液桥接触线的平均曲率,结果表明受到表面张力和轴向重力的液桥与平板间的接触线可以由圆形来表示。Ferrera等[15]采用TIFA方法对表面张力进行了计算并通过实验分析了液桥形状与表面张力之间的关系。Chen等[17]通过实验研究了接触角滞后性对液桥轮廓的影响。
已有数值模型的研究包括对液桥接触线和接触角的描述方法[18-21]。液桥在给定接触角以及忽略重力的情况下可以简化为旋转轴对称模型[18]。Vogel[20]分析了轴向重力对于液桥形状的影响,结果表明轴向重力会导致液桥形状的变形。Chen等[21]建立了能够反映接触角滞后性对液桥形状影响的模型,并发现在给定的平板间距下液桥在平衡状态可能会出现两种不同的形状。
上述关于液桥的研究是针对受表面张力和轴向重力影响的情况。实际换热器竖直翅片间附着的液桥所受的重力方向为沿液桥径向方向。径向重力作用不但会使得液桥接触线沿竖直方向发生伸长现象,还会导致接触线上各点的接触角随着方位角不断变化。已有研究中圆形接触线和等接触角模型难以描述实际换热器中受表面张力和径向重力共同作用的液桥的形状。
本研究目的是基于实验,提出描述径向重力-表面张力耦合作用下竖直翅片间液桥的形状的方程,包括液桥三相接触线方程、接触角方程。
1 实验设计
1.1实验目的
换热器竖直翅片间附着的液桥的形状如图1所示。由于受到径向重力作用,液桥的形状沿z轴方向非对称,从而导致接触线沿竖直方向伸长且接触角不断变化。本文的目的为通过实验观测竖直翅片间的液桥形状,并测量液桥接触线和接触角;在此基础上开发接触线和接触角的定量预测模型,从而实现对液桥形状的描述。
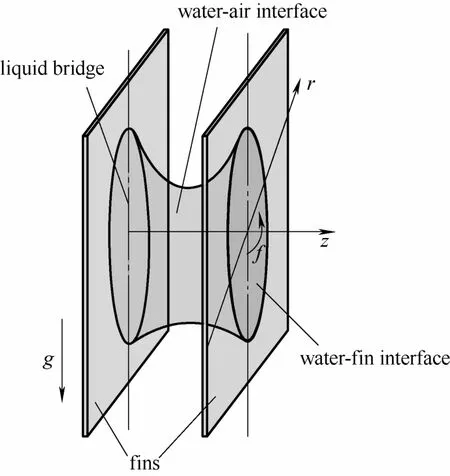
图1 翅片间液桥示意图Fig. 1 Schematic diagram of water bridge between fins
1.2实验装置
为了研究竖直平板间液桥的接触线和接触角,实验装置需要满足以下要求:① 液桥可以在竖直平行平板间形成;② 平板间距可以调整;③ 可以对液桥形状进行观察和记录;④ 可以从不同角度对液桥的接触角进行观察和测量。
根据上述要求,实验装置包括液桥形成系统、平板固定系统、拍摄系统、旋转系统,完整实验装置如图2所示。
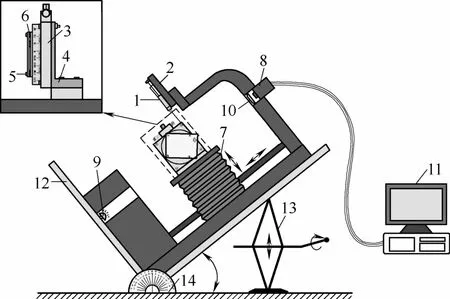
图2 实验装置Fig. 2 Schematic diagram of experimental apparatus1—syringe;2—motor;3—platform;4—bracket;5—retaining nuts;6—shims;7—x-y-z movable platform;8—CCD camera;9—light source;10—microscopic lens;11—computer;12—rotating arm;13—jack;14—protractor
液体注射系统包括自动注射器和步进电机。由于人工注射形成的液桥可以通过人为控制使形成的液桥趋于对称,比冷凝形成的液桥更有利于实验观测,因此本文采用人工注射的方式在平板间形成液桥。其中注射器的精度为±0.02 μl,注射器针头直径为0.3 mm。步进电机可以通过计算机控制开停,从而实现对自动注射器的上升和下降的调节。
平板固定系统包括旋转平台、支架、螺丝、垫片和移动平台。其中旋转平台旋转精度为±10′;移动平台的精度为±0.01 mm,通过移动平台可以实现对平板位置的调节;该系统中的支架可以实现旋转系统和固定系统的连接;平板可以通过螺丝固定在旋转平台上;4种不同的垫片用来调节两个平板之间的间距。平板固定系统各部件结构与安装位置见图3。
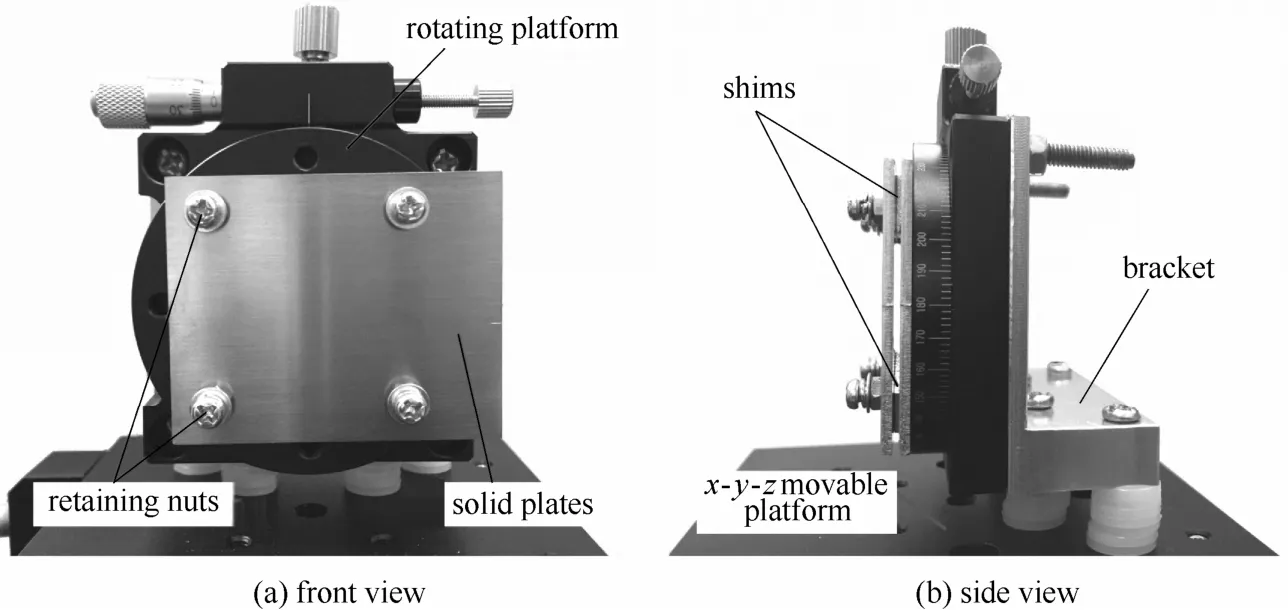
图3 平板固定系统照片Fig. 3 Photos of solid sample fixed system
拍摄系统包括CCD相机、LED冷光源、透镜和电脑。其中LED冷光源可发出亮度可调节的单色光,用来观察液桥轮廓;透镜的放大倍数为0.7~4.5,光学变形率为0.01%;CCD相机分辨率为752×480,可以拍摄液桥轮廓并储存在计算机中。
旋转系统包括旋转架、千斤顶和量角器。旋转架为10 mm厚的不锈钢板;通过千斤顶可以使整个旋转台及旋转台上的系统进行旋转运动;通过量角器控制旋转角度。
1.3实验样件
考虑到换热器翅片上冷凝所形成的液态水可认为是蒸馏水,因此实验液体试样选择为蒸馏水。
本文实验的固体样件采用了5种润湿性不同的材料制成的固体平板,包括铝、铜、不锈钢、光学玻璃、有机玻璃。其中铝、铜和不锈钢是换热器中的常见材料,光学玻璃和有机玻璃是透明的,所以能够方便地观察到液桥的接触线形状。5种材料的润湿性见表1。
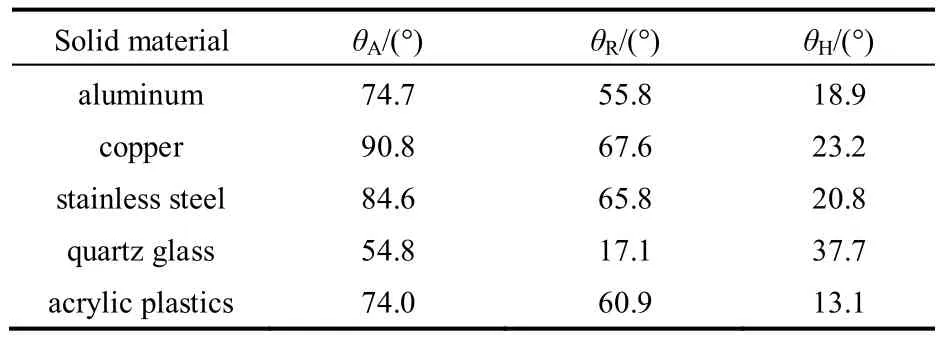
表1 5种固体材料表面的润湿性Table 1 Wettability of five types of solid plane surfaces
1.4实验步骤
详细的实验操作步骤如下。
(1)将平板与旋转平台通过4个螺丝进行连接,连接过程可采用不同厚度的垫片实现竖直平行平板间距的调节。
(2)通过电机以及移动平台使注射器处于合适的位置,注射蒸馏水在竖直平行平板间形成液桥,并通过控制注射器来控制形成液桥的体积。调节透镜和光源使CCD相机可以获得清晰的液桥轮廓图像。
(3)通过调整千斤顶使得旋转架与其他机构一起旋转,同时将旋转平台进行旋转,保证液桥处于竖直向下方向。当量角器达到所需角度后停止旋转并拍摄该角度下的液桥轮廓。
(4)测量不同观察角度下的液桥最大接触角和最小接触角,以及分别测量液桥接触线长轴和短轴的长度。
1.5实验工况与误差分析
为了通过实验对液桥接触线和接触角进行研究,实验工况包括不同液桥体积(3~21 μl)、不同平板间距(0.5~2.0 mm)和不同观察角度(0°~90°)。
接触线长轴和短轴的测量误差可以由像素分析法得出为0.005 mm。接触角的测量误差由接触角测量仪厂商提供为0.1°。
2 液桥接触线的实验结果及预测模型
2.1接触线的实验观察结果
图4是通过CCD相机拍摄的竖直平板间液桥的轮廓。图中液桥体积为6 μl,平板间距为1 mm,平板材料为有机玻璃。
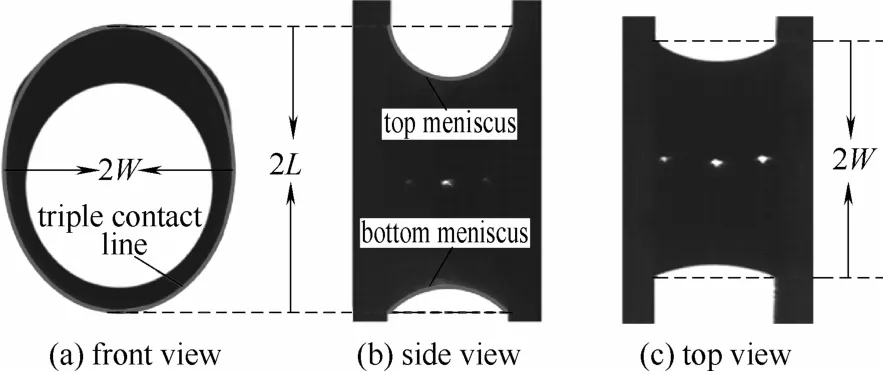
图4 竖直平板间液桥轮廓Fig. 4 Contour of water bridge between vertical plates
从图4(a) 中可得,液桥与竖直平板间的接触线近似为椭圆形。图4(b) 中顶部弯液面与底部弯液面形状不同,此时液桥长度为2L,即为接触线椭圆的长轴长。图4(c) 为液桥的俯视图,即方位角为90°的情况下的液桥轮廓照片,在该视图下液桥的两个弯液面近似相同,液桥此时的长度为2W,即为接触线椭圆的短轴长。
2.2接触线预测模型
根据实验观测结果,接触线可以表达为椭圆方程,该方程在圆柱坐标系下可以表示为
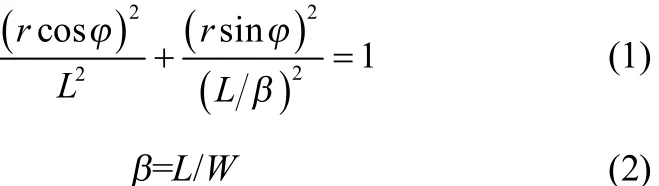
其中,r是椭圆弦长; φ是方位角,和观测角相等; L是长轴长度; W是短轴长度; β是伸长比, 表示液桥在重力方向上的伸长程度。
由式(1)和式(2)可知,影响接触线形状的关键因素是伸长比β。图5显示了不同Bond数Bo下的伸长比,Bo定义如下

其中,ρ是蒸馏水的密度; g是重力加速度; d是平板间距; σ是气液交界面的表面张力;L和W分别是椭圆接触面的半长轴和半短轴。根据实验数据拟合得到伸长比β关于Bo的拟合方程
2.3接触线预测模型的精度验证
如图5所示,伸长比β随着Bo增加而增加,且近似为线性关系。图中共有21个数据点,所有数据点与接触线的预测模型的误差均在±5%的范围内,平均误差为3.4%。
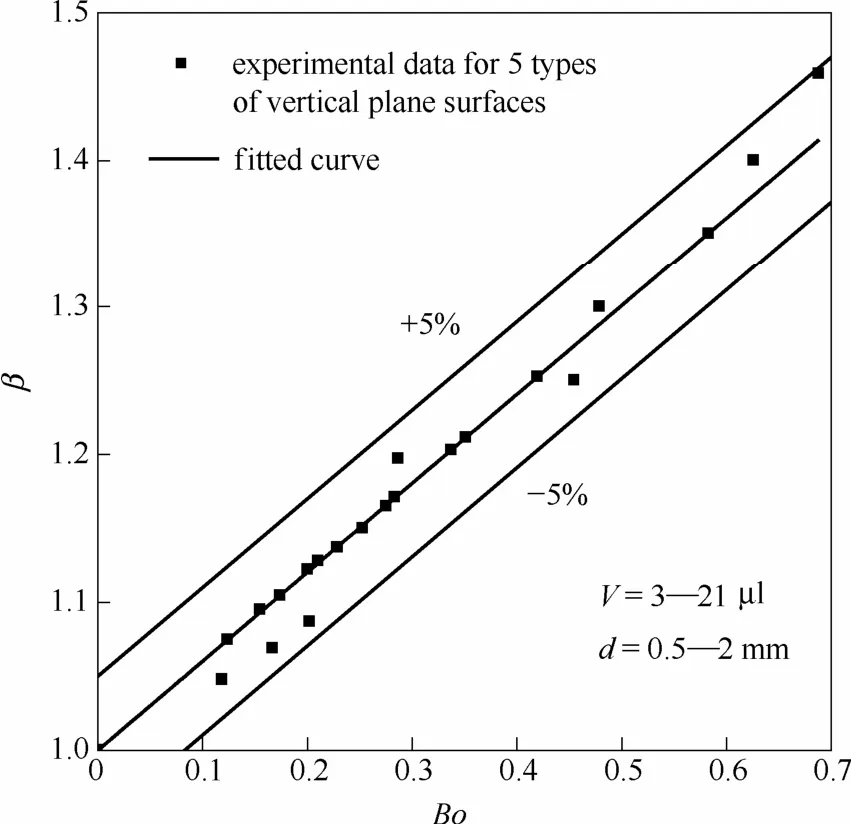
图5 接触线伸长比预测值与实验值的对比Fig. 5 Comparison between predicted results and experimental data of β
3 液桥接触角的实验结果及预测模型
3.1接触角的测量结果及预测模型
根据接触角的测量结果可知,对于不同的平板材料上形成的液桥的接触角与方位角的关系均呈三次方的函数关系
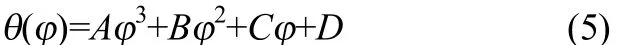
其中,θ(φ)是不同方位角的接触角; φ是方位角; A、B、C、D是待定系数,可根据如下边界条件得到
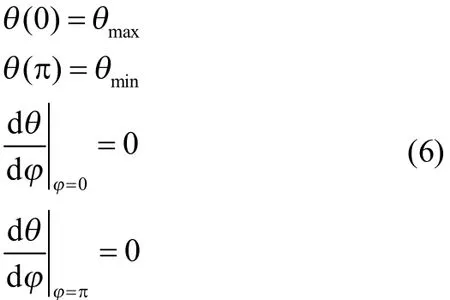
其中,θmax是在φ=0时的最大接触角; θmin是在φ=π时的最小接触角。
由式(5)和式(6)可以计算出待定系数A、B、C和D,如式(7)所示
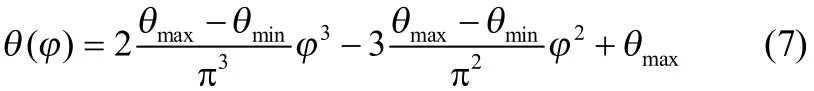
由式(7)可得,最大接触角和最小接触角是计算不同方位角下接触角的关键参数。
根据实验测试结果发现,液桥的最大接触角近似等于水在平板材料上的前进接触角;最小接触角的表达式如式(8)所示,该公式预测值与实验值平均偏差为5.9%。
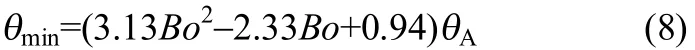
将式(8)代入式(7),可以得到预测液桥接触角的模型,如式(9)所示
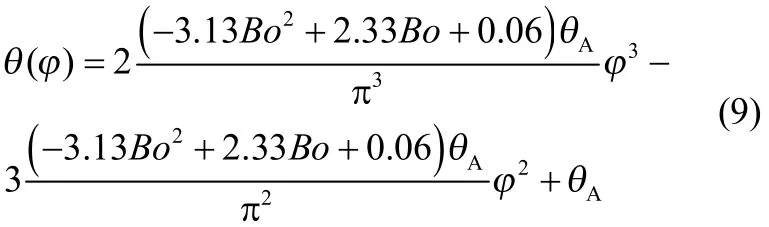
3.2液桥接触角预测模型的精度验证
图6显示了根据式(9)对液桥接触角的预测值与实验值的对比。图中共包含78个数据点,其中有95%的点处于误差±20%的范围内,平均误差为7.9%。从图中可以看出,模型在接触角范围为20°~90°的范围内可以较好地预测液桥的接触角。
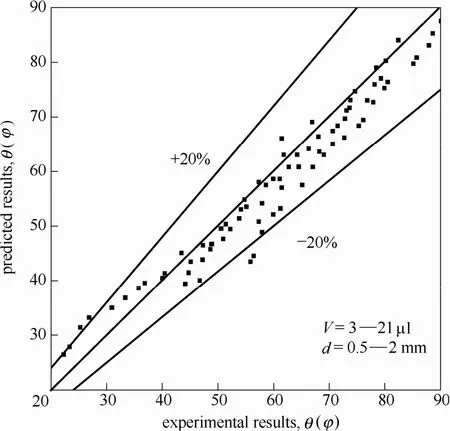
图6 接触角预测结果与实验值的对比Fig. 6 Comparison between predicted results and experimental data of θ(φ)
4 结 论
(1)通过可视化实验对描述竖直翅片间液桥形状的关键参数包括接触线和接触角进行观测发现,液桥接触线形状近似为椭圆形,而接触角与方位角呈三次多项式关系。
(2)开发了基于椭圆方程的液桥三相接触线预测模型,模型对于椭圆伸长比的预测值与实验值的平均误差为3.4%。
(3)开发了基于Bo和翅片表面润湿性的液桥接触角预测模型,模型的预测值与实验值的平均误差为7.9%。
符号说明
Bo——Bond数
d——平板间距,mm
g——重力加速度,9.81 m·s−2
L——长轴长度,mm
p——边界点距离,pixel
r——椭圆半径,mm
V——体积,μl
W——短轴长度,mm
β——伸长比
θ——接触角,(°)
ρ——密度,kg·m−3
σ——表面张力,N·m−1
φ——方位角,(°)
下角标
A——前进
max——最大值
min——最小值
R——后退
References
[1]WANG C C, LEE W S, SHEU W J, et al. Investigation of the airside performance of the slit fin-and-tube heat exchangers [J]. International Journal of Refrigeration, 1999, 22(8): 595-603.
[2]刘金平, 戴绍碧, 叶立平. 析湿工况下波纹翅片管换热器空气侧换热与压降特性 [J]. 化工学报, 2009, 60(10): 2438-2445. LIU J P, DAI S B, YE L P. Air-side heat transfer and friction characteristics of wavy fin-and-tube heat exchangers under dehumidifying conditions [J]. CIESC Journal, 2009, 60(10): 2438-2445.
[3]COMINI G, NONINO C, SAVINO S. Modeling of conjugate conduction and heat and mass convection in tube-fin exchangers [J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2008, 18(7/8): 954-968.
[4]杨艺菲, 庄大伟, 胡海涛, 等. 湿工况下平翅片平面凝水形成及运动过程的数值模拟与实验验证 [J]. 化工学报, 2014, 65(S2): 140-147. YANG Y F, ZHUANG D W, HU H T, et al. Numerical simulation and experimental validation of water condensing and moving on plain-fin surface under dehumidifying conditions [J]. CIESC Journal, 2014, 65(S2): 140-147.
[5]WANG C C,LIN Y T, LEE C J. An airside correlation for plain fin-and-tube heat exchangers in wet conditions [J]. International Journal of Heat and Mass Transfer, 2000, 43(10): 1869-1872.
[6]李娬, 李慧珍, 康海军, 等. 析湿正弦波纹翅片管束的热质交换特性研究 [J]. 西安交通大学学报, 1996, 30(8): 57-63. LI B, LI H Z, KANG H J, et al. Experimental study on heat/mass transfer and pressure drop for dehumidifying sinusoid fin-and-tube heat exchanger [J]. Journal of Xi’an Jiaotong University, 1996, 30(8):57-63.
[7]YUN R, KIM Y B, KIM Y C. Air side heat transfer characteristics of plate finned tube heat exchangers with slit fin configuration under wet conditions [J]. Applied Thermal Engineering, 2009, 29(14/15): 3014-3020.
[8]MA X K, DING G L, ZHANG Y M, et al. Airside heat transfer and friction characteristics for enhanced fin-and-tube heat exchanger with hydrophilic coating under wet conditions [J]. International Journal of Refrigeration, 2007, 30(7): 1153-1167.
[9]郭轶波, 杜志敏, 陈萍, 等. 入口相对湿度对开缝翅片管换热器空气侧换热与压降特性的影响 [J]. 化工学报, 2010, 61(S2): 49-53. GUO Y B, DU Z M, CHEN P, et al. Effect of inlet air relative humidity on air side characteristics of slit fin-tube heat exchangers [J]. CIESC Journal, 2010, 61(S2): 49-53.
[10]ZHUANG D W, HU H T, DING G L, et al. Numerical model for liquid droplet motion on vertical plain-fin surface [J]. HVAC and R Research, 2014, 20(3): 332-343.
[11]马小魁, 丁国良, 张圆明. 析湿工况下带亲水层开缝翅片管换热器空气侧传热传质特性 [J]. 化工学报, 2007, 58(8): 1911-1916. MA X K, DING G L, ZHANG Y M. Airside heat and mass transfer characteristics of split fin-and-tube heat exchangers under dehumidifying conditions [J]. Journal of Chemical Industry and Engineering(China), 2007, 58(8): 1911-1916.
[12]MIN J C, WEBB R L. Condensate carryover phenomena in dehumidifying finned-tube heat exchangers [J]. Experimental Thermal and Fluid Science, 2000, 22(3/4): 175-182.
[13]WANG C C, HSIEH Y C, LIN Y T. Performance of plate finned tube heat exchangers under dehumidifying conditions [J]. Journal of Heat Transfer, 1997; 119(1):109-17.
[14]VERGES M A, LARSON M C, BACOU R. Force and shapes of liquid bridges between circular pads [J]. Experimental Mechanics, 2001, 41(4): 351-357.
[15]FERRERA C, CABEZAS M G, MONTANERO J M. An experimental analysis of the linear vibration of axisymmetric liquid bridges [J]. Physics of Fluids, 2006, 18(8): 082105.
[16]ZHANG F Y, YANG X G, WANG C Y. Liquid water removal from a polymer electrolyte fuel cell [J]. Journal of the Electrochemical Society, 2006, 153(2): A225-A232.
[17]CHEN H, TANG T, AMIRFAZLI A. Effect of contact angle hysteresis on breakage of a liquid bridge [J]. European Physical Journal: Special Topics, 2015, 224(2): 277-288.
[18]VOGEL T I. Stability of a liquid drop trapped between two parallel planes(Ⅱ): General contact angles [J]. SIAM Journal on Applied Mathematics, 1989, 49(4): 1009-1028.
[19]ACERO F J, FERRERA C, CABEZAS M G, et al. Liquid bridge equilibrium contours between non-circular supports [J]. Microgravity Science and Technology, 2005, 17(2): 18-30.
[20]VOGEL T I. Stability of a liquid drop trapped between two parallel planes [J]. SIAM Journal on Applied Mathematics, 1987, 47(3): 516-525.
[21]CHEN H, TANG T, AMIRFAZLI A. Modeling liquid bridge between surfaces with contact angle hysteresis [J]. Langmuir, 2013, 29(10): 3310-3319.
Visualization and prediction model on shape of liquid bridge
ZHUANG Dawei, YANG Yifei, HU Haitao, DING Guoliang
(Institute of Refrigeration & Cryogenics Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract:Water bridge can affect the performance of fin-and-tube heat exchanger working under dehumidifying. In order to know the influence of water bridge on heat exchanger, the shape of water bridge needs to be studied. In this research, a visual experiment was used to develop the prediction model of water bridge shape. Based on the visual experiment, the contact line and the contact angles of water bridge were measured, covering various water volumes, solid plate separations and five different solid materials. The prediction model of contact line via correlated aspect ratio was developed, and the prediction model of contact angles via the correlated maximum and minimum contact angles was proposed. The mean deviation of aspect ratio of contact line was 3.4% and that of contact angles was 7.9%.
Key words:water bridge shape; contact angle; prediction; model; experimental validation
中图分类号:TK 124
文献标志码:A
文章编号:0438—1157(2016)06—2224—06
DOI:10.11949/j.issn.0438-1157.20151707
基金项目:国家自然科学基金项目(51576122);国家自然科学基金创新研究群体科学基金项目(51521004)。
Corresponding author:Prof. DING Guoliang, glding@sjtu.edu.cn

