基于超声波阻抗谱的颗粒粒径表征方法

纪晓明，苏明旭，汪雪，蔡小舒(上海理工大学颗粒与两相流测量研究所，上海市动力工程多相流动与传热重点实验室，上海 200093)



基于超声波阻抗谱的颗粒粒径表征方法

纪晓明，苏明旭，汪雪，蔡小舒
(上海理工大学颗粒与两相流测量研究所，上海市动力工程多相流动与传热重点实验室，上海 200093)

摘要：研究超声反射波谱与颗粒粒径及浓度之间的关系并发展一种基于超声波阻抗谱的颗粒粒径表征方法。对超声波波动理论模型适当变形，建立超声阻抗谱与颗粒粒径及浓度之间的关系；进一步通过数值模拟分析超声阻抗谱对颗粒浓度及粒径变化的敏感性；实验中使用中心频率10～100 MHz超声波换能器，利用自发自收模式对超声波在缓冲层与介质界面上的反射波信号进行测量并分析，对体积中位径分别为7.69、21.58、66.64 µm的聚苯乙烯悬浮液进行实验，获得阻抗谱并与数值模拟结果对比，根据实验阻抗谱进行数据反演获得样品颗粒粒度分布，并与图像分析结果进行了对比，结果显示，本方法可有效分辨3种颗粒样品的粒径。

关键词：超声阻抗谱；聚苯乙烯悬浮液；粒度分布；浓度；测量；数值模拟；反演

2015-12-23收到初稿，2016-03-16收到修改稿。

联系人：苏明旭。 第一作者：纪晓明（1991—），男，硕士研究生。

Received date: 2015-12-23.

Foundation item: supported by the National Natural Science Foundation of China (51176128,5120611).

引　言

颗粒存在于工业中的各个领域，其粒径大小及浓度高低会影响相关医药产品质量、食品保质期、能源利用效率以及设备使用寿命，所以对颗粒特性的表征得到了广泛的关注和研究。目前已有较多方法得到发展和应用，如动态光散射[1]、多波长消光法[2]和图像法[3-6]等，但是上述方法都存在着不足，即对于高浓度颗粒悬浮液不宜直接测量而需要预先稀释，而很多情况下不恰当的稀释过程会额外引入误差或使得待测样品缺乏代表性。由于超声波穿透性较强，利用超声法对浓度相对较高[7]（体积分数大于20%）的颗粒悬浮液进行测量较为合适。

目前，常见的悬浮液颗粒尺寸和浓度超声法测量原理是基于超声衰减谱和相速度谱与颗粒粒径及浓度之间的关系，这一关系在数学上形成超声颗粒粒径表征的理论模型[8-9]。实验中，超声波通过测量区后由换能器接收，通过分析接收信号获得衰减谱和相速度谱，结合模型反演出颗粒粒径及浓度[10-11]。然而，当测量对象浓度更高或介质本身对超声有较强衰减（如甘油）时，可能会由于超声信号衰减太大导致接收换能器无法获得信号，或所获信号信噪比太差，从而影响测量结果的精度甚至不能测量。一种处理方法是尽量减小发射和接收换能器间距（声程），但这一方面可能使得测量区处于近场区，另一方面在很多现场应用中声程不可调。

与透射式测量不同，对超声在缓冲层与介质界面上的反射波信号进行测量时，只要选取合适的缓冲层材料（即恰当的阻抗差）就可以得到信噪比较好的信号，且由于无须考虑超声波在介质中传播过程，所以信号强度对其衰减特性也并不敏感。此外，超声特性阻抗与颗粒介质本身特性紧密相关，原理上利用超声反射波信号表征颗粒特性是可行的。目前已有一些研究从实验角度研究反射信号与被测介质特性，如含气食品中气泡性质的表征[12]、蜂蜜的动态剪切流变性质[13]、静态轴承内润滑油的黏度分布[14]，但是对于颗粒悬浮液中颗粒度进行表征还未见报道。为此，本文研究一种超声阻抗实部谱表征颗粒粒径的方法，并将其与显微镜图像法进行对比。

1　超声阻抗谱颗粒表征原理

1.1超声阻抗原理

由超声颗粒表征中ECAH[8-9]（Epstein-Carhart-Allegra-Hawley）理论模型出发，建立悬浮液中颗粒粒径及浓度与超声阻抗之间的关系。复波数κ表达式如下

式中，κc=2π/λ为入射压缩波波数，φ为介质浓度，R为颗粒半径，n为颗粒粒度分散等级，An为散射系数，由压缩波函数结合边界条件得到。

按照复波数定义

可见，复波数的实部与相速度[c(ω)]有关，而其虚部则等于衰减系数[α(ω)]，其中ω为超声波角频率。超声复阻抗（Z）定义由式（3）[15]给出。

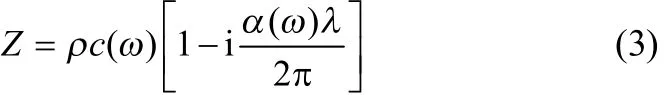
式中，ρ为介质等效密度，λ为超声波波长。联立式(1)～式(3)，有

式中，Re为取实部运算。式（4）建立了超声复阻抗与颗粒特性（如粒径、浓度及密度等）之间的关系。

1.2数值计算

利用表1的物性参数[16]，结合式（4），进行了一系列的数值计算，讨论了聚苯乙烯颗粒-水悬浮液中颗粒的粒径及浓度的变化对超声阻抗实部的影响。模拟中聚苯乙烯颗粒粒径大小为10、30、50、100 µm，聚苯乙烯-水悬浮液体积分数分别为10%、30%和50%。

表1　水、聚苯乙烯物性参数(20℃)Table 1　Physical parameters of water and polystyrene

图1为聚苯乙烯悬浮液中声阻抗实部在不同粒径和浓度条件下随超声频率的变化曲线。每条阻抗谱曲线均对应一特征频率，该特征频率与颗粒对超声波的共振散射有关[17]。低于此频率，阻抗稳定在某一水平值，直至到达该频率时出现明显振荡，信号迅速降至最小值（谷），又迅速升至最大值（峰），之后振荡逐次衰减直至重新趋于稳定。在图1(a)中，该特征频率随着颗粒粒径增大而变小，但曲线之间变化趋势相似。在图1(b)中，改变悬浮液颗粒浓度，振荡幅度(峰值和谷值差)随浓度增加而递增，但其特征频率并无明显变化。简单地说，阻抗谱特征频率和颗粒粒径具有直接关联而其振荡幅度与浓度直接关联。在超声衰减和速度谱方法中，颗粒粒径和浓度会同时影响衰减或速度谱，这使得粒径和浓度被严重地耦合在一起，而阻抗谱中特征频率和幅度的分离使得上述两个参数的检测相对独立，对于降低问题复杂性非常有利。理论上，阻抗谱虚部同样可以用于颗粒表征，但前期分析发现其敏感度较实部低，所以本文只讨论利用阻抗谱实部对颗粒特性进行表征。

图1　聚苯乙烯-水悬浮液中声阻抗谱数值模拟结果（实部）Fig.1　Numerical results of real part of acoustic impedance spectra for polystyrene suspensions

2　实验方法和过程

2.1材料

实验所用的聚苯乙烯标准颗粒由北京海岸鸿蒙标准物质技术有限公司提供，共采用了3种样品，利用光学显微镜分析，其颗粒图像和粒度分布如图2所示。测量结果显示样品1、样品2和样品3的体积中位径分别为7.69、21.58、66.64 µm，同时可见粒度分布范围较窄并且具有较好球形度。

图2 显微镜法实验样品图像和颗粒粒度分布Fig.2　Image and particle size distribution of samples obtained by optical microscopy-based technique

2.2实验装置和方法

图3为实验中测量反射波谱装置。装置基本工作原理和其他超声波谱仪类似[18-19]。其中硬件包括超声脉冲波发射接收仪、超声换能器、悬浮液样品池、双通道高速数字化仪以及用于信号采集和分析的计算机。

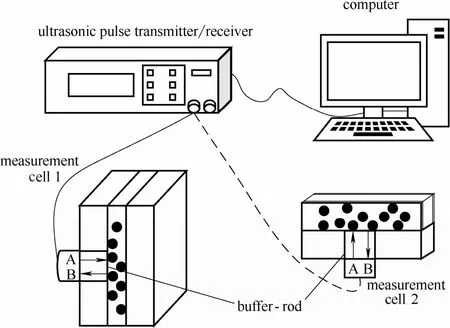
图3　悬浮液颗粒尺寸分布的超声测量装置Fig.3　Sketch of ultrasonic spectrometer used to measure particle size distribution in suspension

由前述数值模拟结果可知，不同颗粒粒径具有对应的特征频率，实验中应选用对应中心频率的超声换能器。尽管商业上已经出现频率1～200 MHz的超宽频扫描式超声波发射和测量设备，但限于目前实验条件，本文针对样品1、样品2和样品3分别选择中心频率为100 MHz (Model V2012 (BC), Panametrics)、30 MHz( Model V356-SU, Panametrics) 和10 MHz(Model V312-SU, Panametrics) 超声换能器。

实验过程如下：在样品池中置入一定量的聚苯乙烯悬浮液（20℃），混合均匀。由超声换能器发出一束超声波A，穿过缓冲层后，在缓冲层与样品的界面处反射形成反射波B，再次经过缓冲层后反射波被同一个超声换能器接收，经分析可获得反射波B对应的幅值（M）和相位(θ)。为计算反射系数，测出声学特性已知的水的超声反射信号作为背景，由式（5）计算反射系数Rs，该法可抵消换能器与缓冲层耦合处产生的声能损失和声场中声发散造成的扩散损失。

式（5）中下角标c和s分别代表标定物和测量样品。利用已知的水和缓冲层的超声特性，在温度为20℃时，以石英玻璃缓冲层的声阻抗为Zdl=1.2× 107kg·m−2·s−1，相对于水的反射系数为Rc=0.7778。将式(5)算得Rs代入式（6）中即可得到复阻抗。

Zs即为实验超声复阻抗。并可按Zs=Zr+iZi分为实部Zr和虚部Zi。

3　实验现象和结果

3.1实验现象与分析

为了分析颗粒对于超声波反射信号的影响，首先对分别安装换能器于样品池侧面和底部(图3)的两类样品池布置方式对比测试，其主要差异在于超声换能器安装位置和颗粒壁面接触形式。实验过程中，由于聚苯乙烯的密度大于水的密度，样品池中颗粒会逐渐沉降并在底部累积，逐渐形成样品池上部浓度逐渐降低，下部则增高情形。图4以样品池1为例示意了两个不同时刻的颗粒分布，应注意一部分聚苯乙烯颗粒会始终附着于壁面而并未下沉。

图4　样品池1内样品的沉降变化Fig. 4　Sedimentation variation of sample in measurement cell 1

对于样品池1，从某一时刻起，按时间间隔60 s，记录颗粒沉降过程中t1～t5时刻接收的超声时域信号，由图5(a)给出。可以看出，不同时刻信号彼此几乎重合，但与背景信号存在一定差别。这说明即便样品池中颗粒浓度变化，所获得的超声时域信号并没有明显差异。而将附着于缓冲层与样品界面处的颗粒去除之后T时刻，再次测量接收到的超声信号BT[图5(b)]，可见其与背景信号完全重合。由此可推断测得声阻抗信号与附着反射界面上的局部颗粒物有关，而与样品区整体的颗粒粒径和浓度并无关系。故后续颗粒表征实验中，均直接以附着在缓冲层表面的颗粒为测量对象，为此采用样品池2进行实验。同时由于测量区域只局限于缓冲层表层，与样品池中其他区域的样品无关，所以本文不讨论峰的展宽；② 理论计算时事先设定了10%体积分数，而实验信号由样品池2获得，其时样品堆积于样品的浓度测量。

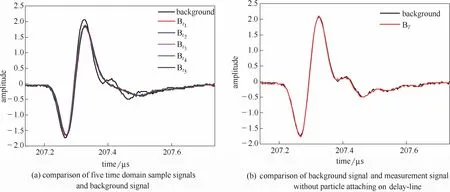
图5　样品信号与背景信号的对比Fig.5　Comparison of signal of samples and background

3.2实验结果及分析

3种样品的实验阻抗谱实部与数值模拟结果对比如图6所示。实验结果与理论曲线趋势基本一致，3种样品的实验阻抗谱在理论特征频率附近都出现了对应的振荡（最大值和最小值）。

图6　3种样品的实验阻抗谱与理论阻抗谱（实部）Fig. 6　Real parts of experimental and theoretical ultrasonic impedance

对比图6(a)、(b)，虽然整体趋势的一致性很好，但还是存在着略微的差别：实验的振荡频率区间（最大值与最小值对应频率差）较理论结果大；同时实验特征频率均比理论值略小；实验结果的幅值明显大于理论结果的幅值。上述差异的存在主要有如下几个原因：① 实验用聚苯乙烯样品颗粒粒径具有一定分布，而理论值仅按其平均粒径计算，造成特征样品池底部致使此处颗粒浓度较高，使得振荡幅度加大；③ 理论模型中并没有考虑声波在颗粒间的复散射，而实验中样品局部浓度会很高，超声与颗粒间的作用也更为复杂。

为了通过超声波阻抗谱分析颗粒粒度分布，采用了一种求解病态方程的ORT算法[2]。该法是在Twomey方法的基础上，利用广义交叉校验（GCV）、L-Curve准则[20]等方式对正则化因子优化的一种独立模式算法。为了用于阻抗谱的反演，在没有改变核心求解过程的同时对系数矩阵计算和导入谱信息进行了改动。对于多分散颗粒系，参照衰减谱方法[16]将阻抗方程离散，并在多频条件下矩阵方程AF=G。

式中，A为系数矩阵；F为离散化的颗粒尺寸频度分布，是待求值；G为实际测得不同频率下的超声阻抗谱实部构成的向量；下角标i、j分别代表粒径和阻抗谱的离散分档数。

图7为实验阻抗谱反演粒度分布曲线与图像法结果的对比。由图可知，超声阻抗谱法很好区分3种不同粒径区间的颗粒。粒度分布范围和图像分析结果也吻合较好，对应表2给出的体积中位径，样品1的结果相对偏差最小。但随着粒径增大，阻抗法与图像法的粒度分布宽度偏差加大，其体积中位径与图像分析结果也存在一定的偏差，但偏差小于11%。对于粒径更大、粒径范围分布更广的样品，大颗粒的沉降较小颗粒快，所以其首先附着缓冲层界面，可能导致测量平均值偏大。

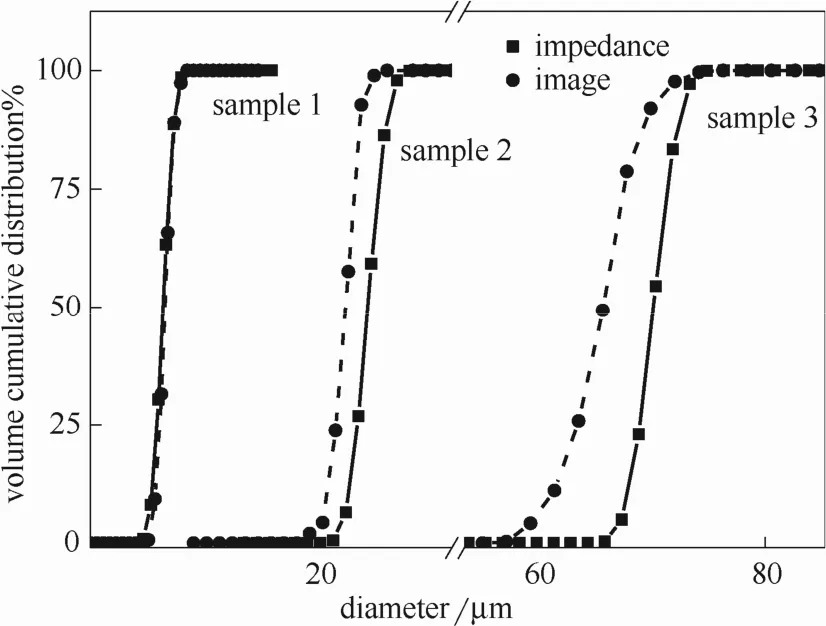
图7　3种样品的超声阻抗谱法和图像法测量结果的对比Fig. 7　Comparison between impedance and image measurement results for three samples

表2　超声谱法与图像法测量样品体积中位径Table 2　Comparison of sample volume median diameter measured by ultrasonic spectrum and image approach

4　结　论

通过阻抗定义对ECAH模型变形，进行了颗粒系超声波阻抗谱数值模拟，发现超声阻抗谱实部对颗粒系特征变化敏感，特征频率随颗粒粒径增大而递减；特征幅度则随浓度增加而递增。设计一种底部入射式样品池装置测量并分析缓冲层与样品界面反射波，通过获得阻抗谱验证了数值结果。根据实验现象初步断定：样品的声阻抗只与附着在缓冲层表面的颗粒特性有关，而与其他区域颗粒无关。利用ORT反演算法求得颗粒粒度分布，3种样品粒度分布区间被很好地区分，与图像法测量结果较为吻合，中位径偏差小于11%。

为了发展超声阻抗法并实现颗粒系的无损、非接触在线测量，理论模型需要进一步考虑声复散射等高浓度效应，实验中应对颗粒运动和颗粒间相互作用对声信号的影响加以研究。

符号说明

A——入射波

An——压缩波散射系数

B——反射波

c(ω)——超声相速度，m·s−1

M——频域信号幅值，V

n——颗粒分散等级

R——颗粒粒径，m

Zs,Zdl——分别为介质阻抗和缓冲层阻抗，kg·m−2·s−1

α(ω)——超声衰减系数，Np·m−1

θ——相位

κ,κc——分别为超声复波数、入射波压缩波波数，m−1

λ——超声波长，m

ρ——悬浮液密度，kg·m−3

φ——悬浮液浓度

ω——超声波角频率，s−1

下角标

c——标定物

s——测量样品

References

[1]WANG X Z, LIU L D, LI R F, et al. Online characterisation of nanoparticle suspensions using dynamic light scattering, ultrasound spectroscopy and process tomography [J]. Chemical Engineering Research and Design, 2009, 87(6): 874-884.

[2]SU M X, XU F, C X S, et al. Optimization of regularization parameter of inversion in particle sizing using light extinction method [J]. Particuology, 2007, 5(4): 295-299.

[3]BLAISOT J B, YON J. Droplet size and morphology characterization for dense sprays by image processing: application to the Diesel spray [J]. Exp. Fluids, 2005, 39(6): 977-994.

[4]CHEN X Z, ZHOU W, CAI X S, et al. In-line imaging measurementsof particle size, velocity and concentration in a particulate two-phase flow [J]. Particuology, 2014, 13: 106-113.

[5]成林虎, 蔡小舒, 周骛. 基于颗粒离焦模糊影像梯度算法的颗粒粒径测量方法[J]. 化工学报, 2012, 63(12): 3832-3838. CHENG L H, CAI X S, ZHOU W . Particle sizing from defocus image of spherical particles by image transition region gradient method [J]. CIESC Journal, 2012, 63(12): 3832-3838.

[6]刘海龙, 陈孝震, 蔡小舒, 等. 基于轨迹图像的气液旋风分离器液滴粒度、浓度、速度的在线测量[J].化工学报, 2012, 63(6): 1729-1734. LIU H L, CHEN X Z, CAI X S, et al. In-line measurement of size, concentration and velocity of drops from gas-liquid cyclone separator based on trajectory image processing[J]. CIESC Journal, 2012, 63(6): 1729-1734.

[7]Measurement and characterization of particles by acoustic methods(Ⅰ): Concepts and procedures in ultrasonic attenuation spectroscopy: ISO 20998-1—2006 [S].

[8]EPSTEIN P S, CARHART R R. The absorption of sound in suspensions and emulsions(Ⅰ): Water fog in air [J]. The Journal of the Acoustical Society of America, 1953, 25(3): 553-565.

[9]ALLEGRA J R, HAWLEY S A. Attenuation of sound in suspensions and emulsions: theory and experiments [J]. The Journal of the Acoustical Society of America, 1972, 51(5B): 1545-1564.

[10]SU M X, CAI X S, XUE M H, et al. Particle sizing in dense two-phase droplet systems by ultrasonic attenuation and velocity spectra [J]. Sci. China Ser. E-Technol. Sci., 2009, 52(6): 1502-1510.

[11]呼剑, 苏明旭, 蔡小舒, 等. 高频宽带超声衰减谱表征纳米颗粒粒度的方法[J]. 化工学报, 2010, 61(11): 2985-2991. HU J, SU M X, CAI X S, et al. Broad-band high-frequency ultrasonic attenuation spectrum method for measuring nanoparticle size distribution[J]. CIESC Journal, 2010, 61(11): 2985-2991.

[12]KULMYRZAEV A, CANCELLIERE C, MCCLEMENTS D J. Characterization of aerated foods using ultrasonic reflectance spectroscopy [J]. Journal of Food Engineering, 2000, 46(4): 235-241.

[13]KULMYRZAEV A, MCCLEMENTS D J. High frequency dynamic shear rheology of honey [J]. Journal of Food Engineering, 2000, 45(4): 219-224.

[14]KASOLANG S, AHMAD M A, DWYER J R S. Measurement of circumferential viscosity profile in stationary journal bearing by shear ultrasonic reflection [J]. Tribology International, 2011, 44(11): 1264-1270.

[15]DUKHIN A S, GOETZ P J. Fundamentals of interface and colloid science [M]//Studies in Interface Science. Amsterdam: Elsevier, 2002: 17-73.

[16]章维, 苏明旭, 蔡小舒. 基于超声衰减谱和相速度的颗粒粒径测量[J]. 化工学报, 2014, 65(3): 898-904. ZHANG W, SU M X, CAI X S. Particle size distribution measurement based on ultrasonic attenuation and phase velocity spectrum [J]. CIESC Journal, 2014, 65(3): 898-904.

[17]HAY A E, SCHAAFSMA A S. Resonance scattering in suspensions [J]. The Journal of the Acoustical Society of America, 1989, 85(3): 1124-1138.

[18]MCCLEMENTS D J, FAIRLEY P. Ultrasonic pulse echo reflectometer [J]. Ultrasonics, 1991, 29(1): 58-62.

[19]MCCLEMENTS D J, FAIRLEY P. Frequency scanning ultrasonic pulse echo reflectometer [J]. Ultrasonics, 1992, 30(6): 403-405.

[20]ELIÇABE G E, GARCÍA R, LUIS H. Latex particle size distribution from turbidimetry using inversion techniques [J]. Journal of Colloid and Interface Science, 1989, 129(1): 192-200.

Particle size characterization based on ultrasonic impedance spectrum

JI Xiaoming, SU Mingxu, WANG Xue, CAI Xiaoshu
(Institute of Particle and Two-phase Flow Measurement, Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract:The purpose of this paper is to explore the relationship between the characteristics of particles and ultrasonic impedance spectra. Although the ultrasonic attenuation and velocity spectra methods are becoming the sophisticated technology for particle size characterization, they are not available in some actual projects, either because the particulate matters to be investigated are too dense or because there are some bubbles inside. However, ultrasonic impedance spectra technology emerges as a potential technique to provide a non-destructively detecting way in the aforementioned occasions. By modifying the ultrasonic attenuation spectral model, the theories related the ultrasonic impedance spectra to particle concentration and size are established to implement quite a few numerical simulations, showing that the acoustic impedances of particles is sensitive to the changes in particle concentration and size. After that, three kinds of polystyrene suspensions with different volume median diameters (7.69 µm, 21.58 µm and 66.64 µm) are investigated experimentally using the transducers with center frequencies varied from 10 MHz to 100 MHz. The results are quantitatively validated by the theory whereby a conclusion can be yielded that it is possible to distinguish the particles with different sizes by using ultrasonic impedance spectra. The comparison of the inversion results and image analysis indicates that the impedance technique is available to particle size characterization.

Key words:ultrasonic impedance spectra; polystyrene suspensions; particle size distribution; concentration; measurement; numerical simulation; inversion

中图分类号：TB 52；O 426.9

文献标志码：A

文章编号：0438—1157（2016）06—2284—07

DOI：10.11949/j.issn.0438-1157.20151954

基金项目：国家自然科学基金项目（51176128,5120611）。

Corresponding author:Prof. SU Mingxu, sumx@usst.edu.cn