扭摆的扭转常数的标定

陈金晶,徐平川,黄安梁

(西华师范大学 物理与空间科学学院，四川 南充　637009)

扭摆的扭转常数的标定

陈金晶,徐平川,黄安梁

(西华师范大学 物理与空间科学学院，四川 南充637009)

摘要：首先通过实验法直接测定了扭摆的扭转常数，并研究了偏转角度对扭转常数的影响。通过多次直接测量的实验数据分析得出，扭摆弹簧的线性情况较好，偏转角对扭转常K有影响，当偏转角在60°—170°范围内，扭转常数的测量符合实验规律。在此基础上，利用扭摆法测定扭摆的转动惯量，则可得出较为准确的转动惯量的测量值。

关键词：扭摆；扭转常数；偏转角度；转动惯量

0前言

刚体是物理学中重要的理想模型，刚体定轴转动是刚体的基本运动形式，描述刚体定轴转动的动量矩和动能都与其转轴的转动惯量成正比。转动惯量作为描述刚体转动惯性的物理量，具有重要的物理意义。在生产生活中，转动惯量也是各类飞行器和其它转动机械重要的物理参数之一，因此准确测量刚体的转动惯量具有重要意义。比较常用的测量转动惯量的方法有扭摆法、三线摆法、复摆法等[1-6]。复摆法和三线摆法的测量系统简单，成本低，但测量精度不高，而且对于大型被测物，装配困难。而扭摆法是这些测量方法当中测量精确度相对较高的一种方法[7]。利用扭摆法测定刚体转动惯量之前，需要精确测定出在一定的偏转角度下扭摆的扭转常数。虽然设备出厂前给出了扭摆常数的参考值，但由于制造精度的原因，不同仪器实际参数并不一致。本文根据扭摆法测量转动惯量的基本原理，通过直接

和间接测量相结合，测量了扭摆的扭转系数，分析了测量的误差，并研究了摆角对扭转常数 值的影响。

1扭摆扭转常数的直接测量

1.1实验原理和实验方法

本实验所用的实验器材是FB729型智能转动惯量综合实验仪和FB213A型计时计数毫秒仪。

将固定在扭摆主轴上的金属细杆在水平面内转过角度θ后，扭摆弹簧的回复力矩与作用在金属细杆上的拉力矩平衡。由力矩公式有M=r×F，其大小为|rFsinα| ，由于实验中作用于金属细杆上的拉力皆垂直于金属细杆，即α=90°，因此拉力矩大小为F·r。

实验中，将金属细杆套在扭摆转轴上，且主轴过杆的中心。在金属细杆两端等距离处分别悬挂两个相同物体作为重垂线(可分别悬挂一定质量的针)。在平整的水平桌面上铺上坐标纸(上面标好0°—170°)，将扭摆置于坐标纸之上并将其转轴对准坐标原点。调整扭摆基座底脚螺丝，使水准仪中气泡居中。保持扭摆转轴对准坐标原点，调整扭摆使细杆两端的重物的指向均在x轴上。用力传感器(首先进行调零)在距离金属细杆中心(扭摆转轴)5cm、10cm、15cm处分别垂直于细杆并拉动细杆，使之偏转一定的角度。偏转角度在30°—60°之间间隔15°测量一组数据，70°—170°之间间隔20°测量一组数据，每组测量重复3次，记下测量结果(偏转角和传感器所示拉力大小)。如图1所示。

1.2测量结果及数据分析

由胡克定律，弹簧受扭转而产生的恢复力矩M与所转过的角度θ成正比，即：

M=Kθ。

(1)

由力矩平衡，F·r=K·θ ，得：

(2)

实验中需要测量在一定的扭转半径r和一定的偏转角θ时，力传感器的示数F。表1是扭摆摆角与传感器所示拉力的实验测量数据。

表1　扭摆摆角与力的实验测量数据

图2所示为扭转半径r分别为5cm，10cm,15cm时，作用在金属细杆上的力矩大小(F·r)与偏转角(摆角) θ之间的关系图。

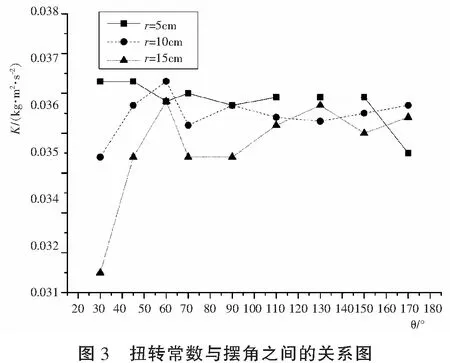
在金属细杆力矩与摆角之间的关系图中，直线的斜率就可表示金属细杆的扭转常数。图2显示，当r=5cm，r=10cm，r=15cm，可得到三条直线，且三条直线几乎重合，表明实验的可靠性较高，重复性较好，扭摆弹簧的线性情况较好。从图中可以看，三条直线均不通过原点，实际应用中可考虑对公式(1)进行修正。

由(2)式，根据实验测量所得数据计算得出的扭转常数，从而得到扭转常数与偏转角之间的关系[8-9](如图3所示)。

由图3可得，当r=5cm时，在30°—150°范围内，扭转常数基本在0.036kgm2/s2上下波动，并且波动范围很小。另外，当r=10cm和r=15cm时，偏转角在60°—170°之间，扭转常数都呈现一定的上下波动变化，由于无明显规律，可认为是实验误差造成的；但偏转角30°—60°之间扭转常数却一直呈现增加的趋势，可认为是由于图2所测得的直线不通过原点造成的。综上所述，偏转角在60°—170°之间，扭摆的扭转常数可认为是满足公式(1)的线性关系。

2扭摆扭转常数的间接测量

2.1实验原理和实验方法

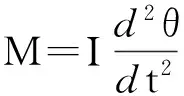
在实验的设计上，需要贴合专业特点，将Access数据库真正的应用到专业领域中，以明确教学目标，在此基础上，还需要注意以下两个方面：

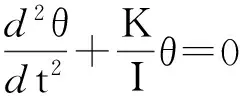
(3)

上式中I表示参与定轴转动的所有连接刚体的总转动惯量，该式描述了满足公式(1)线性关系的扭摆将做简谐振动，振动的周期为：

(4)

(5)

根据(4)式和(5)式，可得扭转常数为：

(6)

因此，只要测出T0、T1、m和D，即可得到K值。

用游标卡尺和物理天平分别测得塑料圆柱体的直径D和质量m；调整扭摆基座底脚螺丝，使水准仪中气泡居中；装上金属载物盘，调节光电探头的位置，使载物盘静止时挡光棒处于光电探头的中央(与发射和接受红外线的小孔在同一竖直方向上)；把计时计数毫秒仪的功能设置为“周期”，把周期次数设置为10 。按下“复位”按钮，根据以上直接测量的结论，偏转角度应在60°以上，可使转盘偏离平衡位置约90°，再按“执行”按钮，松手让载物盘来回摆动，测量载物盘的振动周期T0。重复测量10次，记录数据。将塑料圆柱体垂直放在载物盘上，重复以上步骤，测定振动周期T1。

2.2测量结果及数据分析

测量结果如表2所示。

表2　实验数据

计算得四个测量值的平均值为：

K=3.507×10-2(kg·m2/s2)。

(7)

2.2.1测量结果的误差分析[9-11]

(1)单个测量量T0、T1、m和D的误差分析

数据测量的误差主要有测量过程的随机误差和仪器的精度造成的误差，分别可用A类不确定度σA和B类不确定度σB来表示，测量误差可表示成：

(8)

首先分析随机误差的A类不确定度，根据误差理论，可用平均值的标准偏差来表示：

(9)

根据表1的测量数据，利用(9)式可分别计算得到T0、T1、m和D的A类不确定度的平方：

根据实验中仪器的精度，可分别得出T0、T1、m和D的B类不确定度(仪器误差)：

σBm=0.05g，σBT0=σBT1=0.001s，σBD=0.01mm。

根据以上分析，塑料圆柱体质量m的测量误差(合成不确定度)为：

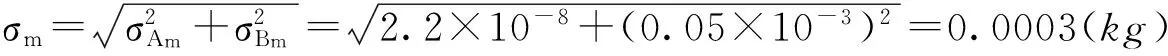
(10)

塑料圆柱体与载物盘一起振动时的周期T1的测量误差为：

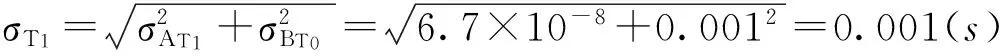
(11)

载物盘的振动周期T0的测量误差为：

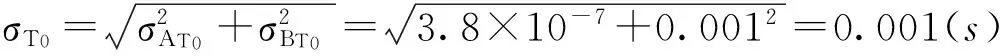
(12)

塑料圆柱体直径D的测量误差为：

(13)

(2)扭转常数K的测量误差

公式(6)两边同时取自然对数后，再求全微分得：

即：

则相对不确定度为：

(14)

将(10)、(11)、(12)和(13)式带入(14)式计算得：

EK=0.26%。

根据(7)式，扭转常数K的测量误差为：

σK=K·EK=3.507×10-2×0.0026=0.009×10-2(kg·m2/s2)。

综上分析，扭摆的扭转常数的测量结果为：

K=K±σK=(3.507±0.009)×10-2(kg·m2/s2)。

(15)

采用以上相同的方法，可对每台扭摆的扭转常数进行标定，为开展刚体转动惯量实验提供较为精确的仪器参数。

3总结

通过对扭摆扭转常数的直接测量和间接测量，测量数据分析表明，间接测量的可靠性较高，扭摆弹簧的线性情况较好，直接测量时，扭摆的偏转角在60°—170°内测得的扭转常数符合测量的数据规律。所以在标定扭摆的扭转常数和使用扭摆法测量转动惯量时，偏转角(摆角)应大于60°，实际操作可取为90°，但不必强调一定取90°。本文在此实验研究的基础上对扭摆的扭转常数进行标定，取得了较为精确的测量结果。在图2中，测量结果显示的力矩和偏转角的关系为直线，但直线并不通过原点，因此需要对M=Kθ的关系进行修正，其影响因素还有待进一步理论探究。

参考文献：

[1]唐光彦，李慧鹏，张春富.扭摆法测量飞行体转动惯量[J].南京理工大学学报(自然学科版)，2008,32(1)：69-72.

[2]葛宇宏，葛志利.三线摆摆线质量对转动惯量精确测量的影响[J].力学与实践，2012,34(6)：51-54.

[3]张国玺，丁俊.三线摆测量物体转动惯量实验方法的改进[J].周口师范大学学报，2014,31(5)：58-61.

[4]申惠娟，陈锺贤.扭摆法测量刚体转动惯量的误差定量分析[J].延安大学学报：自然科学版，2013,39(3)：199-200.

[5]迟占铎，徐鑫莉，张心明.扭摆法测转动惯量的误差分析[J].长春理工大学学报：自然科学版，2012,35(1)：36-42.

[6]薄悦，卢志辉，张磊乐.扭摆法测量转动惯量的误差分析与校准[J].计量技术，2011,(8)：21-23.

[7]池红岩，丁红伟.关于扭摆法测转动惯量实验的改进[J].物理通报，2011,(1)：51-52.

[8]李德禄，林芮竹，王杰，等.摆角对物体转动惯量测量误差的影响[J].中国科技信息，2013,23(4)：32-33.

[9]穆松梅，周鑫媛.摆动法测定物体转动惯量实验中摆动角度对测量的影响[J].高校实验室工作研究，2011，(12):61-62.

[10]贺文阳，刘艳辉.大学物理实验中不确定度的评定[J].湖南工程学院学报，2008,18(2)：53-55.

[11]马亚林，陈建新.扭摆法测物体转动惯量的不确定度分析[J].大学物理实验，2011,24(1)：94-96.

CalibrationoftheTorsionConstantofTwist

CHENJinjing,XUPingchuan,HUANGAnliang

(CollegeofPhysicsandSpaceScience,ChinaWestNormalUniversity,NanchongSichuan637009，China)

Abstract:Firstly,the torsion constant of twist has been directly determined by the experimental method,and the effect on deflection angle has been studied on also in this paper.Through times of direct measurement of experimental data analysis,linear of twist spring is good;deflection angle has influence to the torsion constant;when the deflection Angle 60 °—170 °,torsion constant measuring accords with the experiment.On this basis,the torsional pendulum method is used to determine the torsion moment of inertia twist again.We can get more accurate measurements of moment of inertia.

Keywords：twist;torsion constant;deflection angle;The moment of inertia

文章编号：1673-5072(2016)02-0221-06

收稿日期：2015-06-09

基金项目：西华师范大学基础课改专项(JCKGYB1414)，四川省教育厅科研项目(12ZB324)

作者简介：陈金晶(1992—)，女，四川盐亭人，硕士研究生，主要从事物理学科教学研究。 通讯作者：徐平川(1973—)，男，重庆合川人，副教授，主要从事天体物理、薄膜物理和物理学科教学研究。 E-mail：pcxu@163.com

中图分类号：O4-34

文献标志码：A

DOI：10.16246/j.issn.1673-5072.2016.02.020