极坐标下椭圆环和椭圆盘刚体的转动惯量
黎 磊,蔡 粤,李文军,刘婷婷,万慧军
(井冈山大学 数理学院 物理系,江西 吉安 343009)
刚体定轴转动是大学物理、普通物理力学部分以及理论力学中的重要内容,而其中转动惯量这个知识点有着重要的物理意义,它是物体在转动中惯性大小的量度,其在科学实验、工程技术等领域也是一个非常重要的参量.教材[1]中讨论了匀质的圆环和圆盘刚体对垂直环(或盘)平面且过其中心轴的转动惯量,文献[2-5]在直角坐标系下利用椭圆的参数方程计算了椭圆环刚体绕垂直于环平面且通过中心的轴旋转的转动惯量,文献[6]中用直角坐标法和广义柱面坐标法计算了椭圆柱体绕对称轴转动的转动惯量,文献[7]中用质量投影法讨论了六面体、椭圆盘、椭圆柱、圆台等几种特殊形状匀质刚体绕对称轴转动的转动惯量,文献[8]用质量投影法计算了椭圆柱面刚体绕对称轴转动的转动惯量.本研究直接根据转动惯量的定义,在极坐标系下求解了椭圆环和椭圆盘对垂直环(或盘)平面且过椭圆焦点和过中心的轴的转动惯量,并且数值计算了转动惯量随椭圆离心率的变化关系.本研究计算过程简单,物理图像清楚,是对课本知识的延伸,且有利于学生理解转动惯量的求法以及掌握极坐标的运用.
1 椭圆环和椭圆盘刚体转动惯量的推导
1.1 椭圆环
首先计算椭圆环对过焦点且垂直于环面的转轴的转动惯量JF.如图1(a)所示,以左焦点F为极坐标原点,x轴的正半轴为极轴,将椭圆方程用平面极坐标表示为

图1 椭圆环(盘)示意图
(1)
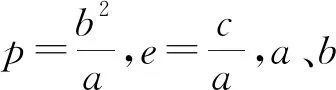
将式(1)代入转动惯量的积分公式得
(2)
其中λ为椭圆环的质量线密度,m为椭圆环的质量,L为椭圆环的周长.
极坐标下弧长的微分为
(3)
对式(3)积分,可以将椭圆的周长表示为
(4)
将(3)、(4)两式代入式(2)中,可得椭圆环对过焦点且垂直于环面的转轴的转动惯量JF:
(5)
接下来,我们计算椭圆环对过中心且垂直于环面的转轴的转动惯量JO.如图1(b)所示,以椭圆的中心为极坐标原点,x轴的正半轴为极轴,可将椭圆方程用平面极坐标表示为
(6)
将式(6)代入极坐标下弧长的微分得
(7)
根据转动惯量的定义,椭圆环对过中心且垂直于环面转轴的转动惯量JO为
(8)
其中,有
(9)
1.2 椭圆盘
(10)
将式(1)代入式(10)可得椭圆盘对过焦点且垂直于盘面转轴的转动惯量:
(11)
同理,求椭圆盘对过中心且垂直于盘面转轴的转动惯量JO时,以椭圆中心为极坐标原点,将式(6)代入式(10),可得
(12)
2 数值分析与讨论
2.1 椭圆环
我们分别数值计算椭圆环对过焦点F和过中心O且垂直环面的转轴的转动惯量JF和JO随椭圆离心率e的变化关系.固定a=3,m=10,作出椭圆环的JF-e,JO-e曲线,如图2、图3所示.

图2 椭圆环转动惯量JF随离心率e的变化曲线

图3 椭圆环转动惯量JO随离心率e的变化曲线
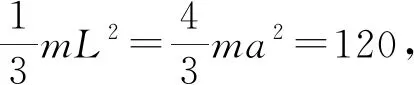
2.2 椭圆盘
接下来,我们分别数值计算椭圆盘对过焦点F和过中心O且垂直盘面的转轴的转动惯量JF和JO随椭圆盘离心率e的变化关系.固定a=3,m=10,作出JF-e和Jo-e曲线,如图4、图5所示.

图4 椭圆盘转动惯量JF随离心率e的变化曲线
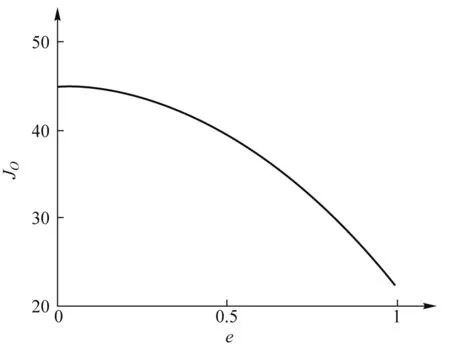
图5 椭圆盘转动惯量JO随离心率e的变化曲线
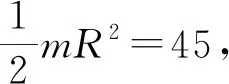
3 小结
本文利用极坐标系巧妙地求解了匀质椭圆环和椭圆盘对过焦点和过中心且垂直于环、盘面的转轴的转动惯量,并数值计算了固定质量和长轴时,转动惯量随椭圆离心率的变化关系.发现随着离心率的增大,椭圆环对过焦点且垂直于环面转轴的转动惯量也开始增大,但在离心率快到1时,会出现一小段下降.而椭圆环对过中心且垂直于环面转轴的转动惯量随着离心率的增大而减小.此外,椭圆盘对过焦点且垂直于盘面转轴的转动惯量随着离心率的增大而增大,而其对过中心且垂直于盘面转轴的转动惯量则随着离心率的增大而减小.本方法计算过程简单,物理图像清晰,本研究不仅是对大学物理、普通物理以及理论力学课本上圆环和圆盘转动惯量知识点的扩充,也有利于学生更深刻地理解转动惯量的定义,掌握转动惯量的计算方法.另外,极坐标的运用让学生深刻理解极坐标系解决问题的优势.数值分析的过程则有利于激发学生学习兴趣,培养学生独立探索、创新研究和思维发散的能力,提高教学质量.

