基于三角模糊数的不确定性数据聚类算法

陆亿红,翁纯佳

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

基于三角模糊数的不确定性数据聚类算法

陆亿红,翁纯佳

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

摘要：随着对实验精确度要求的不断提高，聚类分析中的不确定性数据聚类也越来越受到关注.然而经典的不确定数据聚类通常假设其概率密度函数(PDF)等信息是已知的，而现实过程中，这些指标并没有那么轻易就能获取.考虑到这些情况，可以利用三角模糊数来恰当有效地表示多维不确定性数据，并采用基于三角模糊数的低计算复杂度的距离计算方法，结合K-means基础聚类方法形成一种被命名为UTDK-means(Uncertain triangular fuzzy number data K-means)的聚类方法，而它是基于三角模糊数的.实验结果表明：基于三角模糊数的不确定数据聚类是可行的，具有一定的研究价值.

关键词：不确定性数据;三角模糊数;聚类算法

近几年来，互联网信息技术不断更新发展，出现了很多机遇和挑战.而在无线传感器网络[1](Wireless sensor network，WSN)等领域，由于各种缘故引起的不确定性问题，产生出一种新的数据类型——不确定数据，在实际系统中，随着对结果精确度的要求不断加强，不确定数据也越来越严重地影响到了系统的可信度和稳定性[2].不确定数据的聚类一般可以划分成两种：一种是存在型的不确定数据聚类，也就是说关系数据库中的数据元组存在与否是有一定的概率的，当然不同元组的概率性也是会相互影响的.另一种是值的不确定性数据聚类，也就是说元组数目和类型己经确定，但是属性值中存在的有一定的误差，以至于产生不确定信息，一般通过概率密度函数(也就是PDF)或其他统计量(如协方差、方差等)进行表示.在不确定数据聚类研究中，一般都是基于PDF建模的不确定性数据[3].笔者研究的是基于值的不确定性但不是基于PDF建模的不确定性数据.

聚类分析属于数据挖掘中的一个热门研究方向，是一种无监督的学习方法[4].通过聚类算法可以将对象集合中相近或者相似的对象聚集到同一个类中，最后得到几个不同的类划分[5].聚类分析分为基于划分、基于层次和基于密度等方面,每个领域都有新突破[6].这几年聚类分析也面临着不确定数据的挑战，因为在研究不确定数据的聚类问题时，传统的聚类算法已经无法胜任.关于不确定数据聚类, Michael Chau等首先在基于K-means算法的基础上提出了一种不确定聚类算法,即UK-means算法,S.D.Lee等对UK-means进行了改进,提出了一个新的算法,即CK-means算法,之后还有K-medoid等不确定性聚类改进算法的出现，然而都是采用整个数据的PDF来表示数据的不确定性[7-9].事实上，数据完整的PDF是比较难得到的，而很多不确定数据常常以三角模糊数的形式来表示[10]，所以笔者专门研究用三角模糊数来表示的一类不确定数据，并采用新的三角模糊距离度量，设计出一种复杂度较低、聚类效果较好的不确定聚类方法：UTDK-means.

1相关定义

记R+为正实数集,F(R+)为全体正模糊数集,R为实数集,F(R)为全体模糊数集.下面是关于三角模糊数的一些概念.

定义1[11]设α∈F(R),且

式中：α=(l，m，u)为三角模糊数；l和u分别为α的上界和下界；(m-l)和(u-m)分别为α的下限和上限，m为三角模糊数α的主值，是可能性最大的值．当(u-l)越大时，三角模糊数α=(l，m，u)就越模糊．当l=m=u时，α成为了普通意义上的实数．

对于任意两个三角模糊数α1=(l1，m1，u1)，α2=(l2，m2，u2)，据扩张定理可知，相应的三角模糊数的运算规则[12]为

α1+α2=(l1+l2，m1+m2，u1+u2)

α1-α2=((l1-u2)∨0，m1-m2，u1-l2)

α1×α2=(l1×l2，m1×m2，u1×u2)

α1∕α2=(l1/u2，m1/m2，u1/l2)

λ×α2=(λ×l2，λ×m2，λ×u2)λ∈R且λ>0

根据定义2，可以计算出两个三角模糊数之间的距离，但是观察可知：计算出来的距离是一个定值，而不是一个新的三角模糊数，在对不确定数据进行聚类的时候这样的结果很有可能产生较为不精确的结果，所以有必要定义一种新的三角模糊数距离公式.

定义3(三角模糊数的新距离)对于给定的三角模糊数α=(mα-xα，mα，mα+yα)，β=(mβ-xβ，mβ，mβ+yβ)，其中mα，xα，yα，mβ，xβ，yβ∈R，在任意维度j(1≤j≤d)上，这两个三角模糊数之间的距离有四种可能性，如图1(a～d)所示.在维度j上，当两个数是如图1(a)所示的相离状态时，可知他们之间的距离的最大值可表示为|mβ-mα+yβ+xα|，最小值可表示为|mβ-mα-yα-xβ|；当两个数是如图1(b)所示的相接状态时，可知他们之间的距离的最大值可表示为|mβ-mα+yβ+xα|，最小值可表示为0；当两个数是如图1(c)所示的相交状态时，可知他们之间的距离的最大值可表示为|mβ-mα+yβ+xα|，最小值可表示为0；当两个数是如图1(d)所示的相包含的状态时，可知他们之间的距离的最大值可表示为|mβ-mα+yβ+xα|，最小值可表示为0.综合讨论后可得计算式为

图1　四种距离状态Fig.1　Four distance state

(1)

(2)

Dmid=|mβ-mα|

(3)

式中：Dj.min为j维上的三角模糊距离中的下界；Dj.max为j维上的三角模糊距离中的上界；Dj.mid为j维上的三角模糊距离中的主值.则两个d维的三角模糊数之间的距离D=[Dmin，Dmid,Dmax]可重新定义为

(4)

式(4)为一个新的三角模糊数距离公式，此时计算出来的三角模糊数之间的距离仍是一个三角模糊数，相比之前，保留了数据的不确定性.

为了将距离度量有效地运用到聚类算法中去，此时再利用定义3，将D转换，得到两个三角模糊数之间的距离，其表达式为

(5)

2UTDK-means聚类算法

2.1算法描述

对N个d维三角模糊数表示的不确定性数据的聚类，就是利用新的三角模糊数间的距离定义，基于K-means的基本聚类方法，最终找到K组分别以点cj(1≤j≤K，K为聚类数目)为簇中心的集合Cj(1≤j≤K).对于聚类结果，一般情况下原则是不同簇成员间的距离则越远越好，Cj集合内各个点到簇中心cj的距离则是越近越好.UTDK-means算法就是基于K-means算法和新三角模糊数距离公式结合得到的多维不确定性数据的聚类算法，K组簇中心分别表示为c1，c2，…，ck，K个簇分别表示为C1,C2,…，Ck.算法描述如下：

1) 随机分配初始簇中心c1至ck

2) Repeat

3) Fori=1 toNdo

4) 计算每一个非中心点到簇中心cj的三角模糊距离Dij，分配距离D最小的数据点Xi给cj

5) end for

6) forj=1 toKdo

7) 重新计算簇Cj的中心点cj

8) end for

9) 簇中心不再改变

10) returnC

2.2计算复杂度

根据上文推导出来的新的三角模糊数距离公式(5)的组成部分，与经典的不确定数据聚类算法UK-means算法进行时间复杂度的比较.UK-means算法的距离公式为

Bsinθ+C)rdθdr

(6)

式中：c=(p,q)为簇中心；假设f(r，θ)是圆不确定区域的概率密度函数，(h，o)为圆心；B=2r(o-q)；A=2r(h-P)；C=r2+(h-P)+(o-q).

UTDK-means和UK-means算法虽然采用不同的距离公式，但是总的来说都是基于K-means算法的，而一般K-means算法的时间复杂度可表示为o(tKn)，t为算法循环的次数，K为簇的组数，n为数据点的个数[14].

充分考虑UTDK-means和UK-means算法的各自的距离公式，可以计算出在二维空间它们各自的总计算量，如表1所示.

表1两种算法的距离计算量比较

Table 1Comparison about the computing distance of two algorithms

计算步骤UK-meansUTDK-means加法89乘法116双重积分10

由表1分析可知：在计算两不确定数据点之间的距离时，UTDK-means所用到的计算量比UK-means用到的计算量要小，因此整个算法的时间复杂度也是比较小的.运用UTDK-means算法，不仅没有对PDF指标的需求，而且有着比较小的时间复杂度，所以是有较大的研究推广价值的.

3实验分析

算法由Matlab实现，运行的硬件环境为Intel(R) Core(TM) i3-M350 2.27 GHz CPU，内存为4 GB，硬盘为500 GB，操作系统为Windows 7.

3.1聚类准确度

准确率(Accuracy)的定义：对于某个数据集，结果集正确分类的样本数据点数目与总样本数据点数目之比，较高的准确率表明聚类结果具有很高准确度.

3.2人工数据集

图2　人工数据集聚类效果Fig.2　Clustering performance of artificial data set

3.3UCI数据集

UCI数据库是一个常用的标准测试数据集，这个数据库目前共有187个数据集，用其中的某些经典数据集做实验是比较有说服力的.Wine，Iris和Glass就是属于经典的被广泛使用的UCI数据集，其中Iris是一种统计数据集，分别对莺尾属植物的萼片宽度、萼片长度、花瓣宽度和花瓣长度等4种属性进行统计，总共有150个数据点；Wine数据集统计了3种不同意大利葡萄酒的化学分析结果，分为13种属性，总共有178个数据点；Glass数据集中通过10种化学成分的值来描述每一种玻璃，分为10种属性，总共有214个数据点.表2列出了这3种数据集的主要特性.

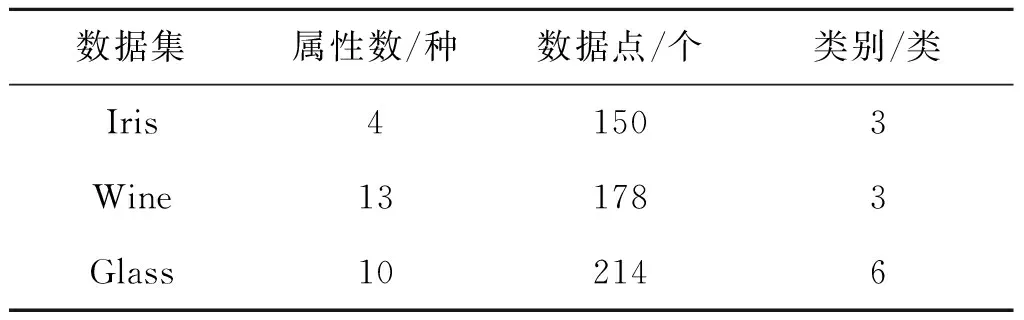
表2　实验中用到的数据集

对3类UCI数据集进行不确定性处理后分别运行UTDK-means算法10次，并且将三类数据集分别运行K-means算法10次，得到的准确率，并取其平均数,结果如表3所示.

表3　UCI数据集聚类效果

经过人工生成的数据集和三种经典UCI数据集对UTDK-means算法的反复实验，并由准确率作为结果指标，可以发现，算法能在较低的时间复杂度下实现较好的聚类效果.并且Iris和Wine是三维数据集，Glass是六维数据集，所以UTDK-means是一个基于三角模糊数，支持多维不确定数据集，低时间复杂度，并且不依赖概率密度函数的聚类算法，有较大的研究推广价值.

4结论

基于三角模糊数表示的多维不确定数据，针对概率密度函数(PDF)等指标信息在很多实际问题中较难获取的情况，充分利用三角模糊数的不确定性，设计一种新的三角模糊数间的距离，保留其特定的不确定性，并在此基础之上，提出了UTDK-means——一种基于三角模糊数的聚类算法.同时分别在经过不确定化的人工数据集和三种不同的UCI数据集上运行UTDK-means算法，比较了聚类结果的准确度的值，得到了比较满意的结果.但由于算法还是基于划分的聚类方法，所以不能对任意几何形状的数据集进行聚类.所以，可以研究更多不同形状分布的数据集基础上UTDK-means算法的运用情况，看是否能够推广到基于密度的聚类方法等.

参考文献：

[1]彭字，罗清华，彭喜元．网络化测试体系中不确定性数据处理方法浅析[J]．仪器仪表学报，2010，31(1)：229．

[2]黄美发，景晖．基于拟蒙特卡罗方法的测量不确定性度评定[J]．仪器仪表学报，2009，30(1)：120-125．

[3]张亚昕,不确定数据聚类算法研究[J].计算技术与自动化.2013，32(2)：60-63.

[4]曾淦宁,吴国权,徐晓群.多元聚类分析方法在杭州湾水质分析上的应用[J].浙江工业大学学报，2009，37(1):14-19.

[5]陆亿红.基于聚类的数据流挖掘技术的分析与研究[J].浙江工业大学学报，2007，35(3):288-291.

[6]RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science,2014,344(6191):1492-1496.

[7]任世锦．基于区间数的不确定性数据挖掘及其应用研究[D]．杭州：浙江大学，2006：3-29．

[8]邱志平．不确定参数结构静力响应和特征值问题的区间分析方法[D]．长春：吉林工业大学，1994．

[9]MICHAEL C,REYNOLD C,BEN K,et al. Uncertain data mining: an example in clustering location data[C]//Pacific-asia Conference on Advances in Knowledge Discovery & Data Mining. Berlin Heidelberg: Springer,2006：199-204.

[10]NGAIWK，KAO B，CHUI C K，et a1．Efficient clustering of uncertain data[C]//Proceedings of the 22nd IEEE International Conference on Data Mining. Hong Kong：IEEE Computer Society，2006：436-445．

[11]李光博，黄德才.基于灰色关联分析的三角模糊多属性决策法[J].浙江工业大学学报，2011，39(2):224-227.

[12]冉静学.三角模糊数排序方法的研究[J].中央民族大学学报(自然科学版),2011，20(4):37-42.

[13]许谦.确定模糊评价综合因素权重的一个方法[J].大学数学,2005,21(1):25- 30.

[14]GULLO F, PONTI G, TAGAERLLI A. Clustering uncertain data via K-medoids[C]//International Conference on Scalable Uncertainty Management. Berlin Heidelberg: Springer，2008：229-242．

[15]姜艳萍,樊治平.三角模糊数互补判断矩阵排序的一种实用方法[J].系统工程,2002,20(2):89-92.

[16]YUN C H, YANG J. Reducing UK-Means to K-Means[C]//In Proceedings of the 6th IEEE International Conference on Data Mining. Omaha: IEEE Computer Science，2007：483-488．

(责任编辑：陈石平)

Research on the clustering algorithm of uncertain data based on triangular fuzzy number

LU Yihong, WENG Chunjia

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:With the increase in the requirements of experimental accuracy, uncertain data clustering method in cluster analysis has more and more attention. Classic uncertain data clustering is generally assumed that the probability density function (PDF) and other information is known, but the reality of the process, these indicators are not so easily able to obtain. In view of this issue, we use triangular fuzzy number to represent the multi-dimensional uncertain data. and the distance calculation method with the low computational complexity based on triangular fuzzy number is combined with K-means method to form a new method called UTDK-means. The experimental results show that the clustering method based on triangular fuzzy number is efficient and worthy to study.

Keywords:uncertain data; triangular fuzzy number; clustering algorithm

收稿日期：2016-01-11

基金项目：水利部公益性行业科研专项(201401044)；国家科技支撑计划项目(2012BAD10B01)

作者简介：陆亿红(1968—)女，浙江永康人, 副教授,硕士, 研究方向为数据库应用和数据挖掘,E-mail:lyh@zjut.edu.cn.

中图分类号：TP3

文献标志码：A

文章编号：1006-4303(2016)04-0405-05