基于PCA-FOA-SVR的股票价格预测研究

王卫红，卓鹏宇

(浙江工业大学 计算机科学与技术学院， 浙江 杭州 310023)

基于PCA-FOA-SVR的股票价格预测研究

王卫红，卓鹏宇

(浙江工业大学 计算机科学与技术学院， 浙江 杭州 310023)

摘要：研究股票价格预测问题，针对影响股票价格因素多存在数据冗余，传统方法无法消除数据冗余，准确稳定预测股价非线性变化.为提高预测精度，在传统的支持向量机回归(Support vector regression, SVR)方法的基础上引入主成分分析(Principal component analysis, PCA)和果蝇算法(Fruit fly optimization algorithm, FOA)，提出了一种PCA-FOA-SVR的股票价格预测方法.首先利用PCA对影响股票价格的因素进行分析降维，消除冗余信息，然后用果蝇算法优化SVR的参数，利用优化后的SVR对非线性变化的股票价格建模预测.最后利用PCA-FOA-SVR模型对宁沪高速(600377)股票价格数据进行仿真实验.实验结果表明：与传统的BP和SVR相比，PCA-FOA-SVR模型在股票价格预测中进一步减小了预测误差，有更高的预测精度，是一种有效可行的股票价格预测方法.

关键词：主成分分析；支持向量回归机；果蝇优化算法；股票价格预测

股票市场价格是反映经济动向的晴雨表，对股票价格的准确预测可以引导市场平稳运行，降低风险，也可以使投资者最大限度地规避风险，做出正确的投资策略，获得最大收益.由于受到政治、经济和社会等各种因素的综合影响，股票价格波动大，变化异常复杂，因此准确把握股票价格的运行态势一直是金融领域的研究重点.

国内外学者对股票价格预测进行了深入的研究，提出了各种预测方法.时间序列分析是最先应用于股票价格预测的方法，文献[1]对股票开盘价格建立ARMA模型，对股票开盘价进行短期预测.由于受到各种因素的影响，股票价格呈现出非线性变化，基于线性模型的时间序列分析法不能很好地反映股票非线性变化规律，预测精度低，应用受限.随着人工智能技术的兴起，BP神经网络因为其强大的非线性映射能力被广泛应用在股票价格预测中.文献[2]提出一种基于BP神经网络的股票价格预测模型SPPM，对股票价格建立多个神经网络模型进行预测.神经网络在非线性的股票预测中取得了良好的效果，但同时存在着学习记忆不稳定，收敛速度慢，容易陷入局部最优值的问题.支持向量机回归(SVR)作为一种新型的机器学习算法[3]，可以克服神经网络过拟合，小样本，局部最小值等缺陷，被越来越多地运用在股票价格预测中[4-5].由于SVR对参数选取敏感，合适回归参数的选取对SVR模型预测精度有着决定性作用，但目前没有有效的理论指导原则.文献[6]用粒子群算法对支持向量机的参数进行优化，文献[7]用遗传算法优化搜寻支持向量机的各项参数，粒子群算法和遗传算法为SVR参数的选取提供了一定的指导，但容易陷入局部最优值.笔者提出了一种利用果蝇算法优化支持向量回归机参数的股票价格预测方法(PCA-FOA-SVR).果蝇优化算法[8]是Pan受果蝇觅食行为的启发而推演出来的一种群体智能优化算法.该算法参数设置简单，适应性强，搜索效率高，相比其他智能算法全局寻优能力强，不容易陷入局部最优值.这里，笔者采用果蝇算法来优化SVR的参数，同时利用主成分分析法对SVR的输入维数进行分析降维，提取主成分，消除输入数据的冗余，以简化网络结构，提高预测精度.在传统支持向量机回归的基础上通过引入主成分分析和果蝇算法，克服股票价格数据冗余，有效解决SVR参数难以选择的问题，为股票价格预测提供了一个新的途径.用PCA-FOA-SVR股票预测模型对股票价格进行预测仿真，并与其他模型对比，验证模型的有效性.

1PCA-FOA-SVR模型

1.1建模基本思想

股票市场作为一个复杂的动态非线性系统，对股票价格的预测一直是研究者关注的重点.股票预测的基本思想一般是利用股票价格的历史数据对股票未来的价格进行预测判断[9].但影响股票价格的因素很多，包括历史数据，技术指标，市场因素等，这些数据之间往往存在着高度冗余，选取影响股票未来价格的有效因素对股票预测至关重要，如果将所有数据都作为网络的输入，则会增加网络复杂度，延长网络训练时间.PCA可以消除数据之间冗余，有效选取影响股票价格的主成分，因此先利用PCA进行数据分析，降低输入维数，提高训练样本有效性.SVR作为后来发展起来的机器学习算法，可以克服神经网路的缺陷，被越来越多地用在非线性时间序列领域，尤其是SVR良好的泛化能力在处理非线性股票价格的预测中有着较大的优势，因此利用SVR对PCA分析后的输入变量进行建模预测.然而，利用SVR的优势进行股票价格预测的前提是选择合适的回归参数，股票价格预测精度与回归参数的选取有着紧密的联系.SVR参数选取的过程实质是一个搜索优化的过程.果蝇算法作为一种全新的群体智能优化算法，考虑到其算法简单，搜索效率高，收敛速度快，在参数寻优方面有着独特的优势，因此这里采用果蝇算法对SVR的参数进行寻优处理，用优化好后的SVR模型对股票价格进行建模预测.算法流程图如图1所示.

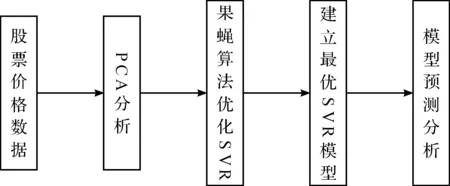
图1　PCA-FOA-SVR算法流程图Fig.1　Flow chart of PCA-FOA-SVR algorithm

1.2主成分分析

主成分分析[10](PCA)是一种利用原始变量之间的相关性，通过原来变量的少数几个线性组合解释原始变量来实现降维的多元统计方法.在股票价格预测问题的研究中，影响股票价格的因素很多，有些对结果的影响大，有些对结果的影响小.主成分分析法就是把影响股票价格的几个因素集中到某几个综合指标(也就是主成分)上，原始变量通过线性组合来反应每一个主成分，主成分之间互为正交，用几个主成分尽可能多地反映原有变量所包含的信息，继而可以缩短多变量时间序列的维数，去除冗余信息，减少隐含在多变量时间序列中的部分噪声，使问题大大简化[11].主成分的求解步骤如下：

1) 确定分析变量，搜集数据资料.

假设有一样本，含有n个样本、p个变量，用自变量矩阵X(n×p)表示样本集.

2) 对原始数据进行标准化变换.

原始数据标准化是为了消除由于量纲的不同可能带来的一些不合理影响.

标准化后的自变量为

(1)

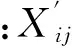
3) 计算原始观测变量样本数据矩阵X经标准化变换后的协方差矩阵R，计算式为

(2)

4) 计算协方差矩阵R的特征值矩阵L和特征向量矩阵A，计算式为

RA=AL

(3)

5) 根据特征值矩阵L和特征向量矩阵A分别计算变量的主成分贡献率及累计贡献率.由累计贡献率的大小来判定主成分的个数，一般要求累计贡献率不小于85%.贡献率和累计贡献率的计算式分别为

(4)

(5)

6) 根据确定的主成分替代原始数据.

1.3支持向量机回归

支持向量机回归问题可以解释为：根据输入-输出数据集(xi,yi)(i=1,…,M),来求取输入和输出之间的关系.其中，xi是第i个m维输入向量，yi是第i个输出标量，M是训练样本数.

在支持向量回归中，首先将输入向量通过一个非线性映射φ(x)映射到一个高维特征空间，然后在高维特征空间中构造优化超平面，进行线性回归，线性回归函数表现形式为

f(x)=〈w,φ(x)〉+b

(6)

式中：w为超平面的权值向量；b为偏置量.SVR实质上是一个优化问题，可以通过最小化目标函数，目标函数式[12]为

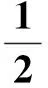
s.t.

yi-f(xi)≤ξi+ε,i=1,…,k

(7)

这是一个二次优化问题，引入拉格朗日函数，将二次优化问题转化为其对偶形式为

s.t.

(8)

解二次优化的对偶形式，可以得到a的值，其中ω的表达式为

(9)

因此回归函数的表达式为

(10)

计算b的值，按照Kuhn-Tucker定理，根据不同的约束条件，可由不同的表达式计算得出，即

(11)

1.4基于果蝇算法的SVR参数优化

SVR模型参数的选取对模型的预测精度和推广能力有着决定性影响.SVR的参数一般有不敏感系数ε，惩罚因子c，核函数参数g等[13].不敏感系数控制函数拟合误差大小，与支持向量机的数目有着密切关系：ε过大，会使支持向量机数目变少，进而会降低模型预测精度；ε过小，支持向量机数目多，导致模型复杂，推广能力差.惩罚因子c影响着模型的复杂度和稳定性：c取值大，学习精度高，泛化能力差；c取值小，对经验误差的惩罚小，训练误差变大.核函数参数影响着学习样本在空间分布的复杂程度：g取值大，模型的预测精度得不到保证；g取值小，模型复杂，推广能力受限.因此如果选取的参数合适，就可以得到稳定准确的回归模型.

果蝇优化算法是根据果蝇独特的觅食行为而推演出来的一种全新群体智能优化算法.果蝇有着优于其他物种的嗅觉和视觉，在寻找食物过程中，首先根据空气中食物的气味来搜寻食物的来源，当飞近食物后再利用其敏锐的视觉来定位食物和种群其他果蝇的位置，并往该方向飞去.

利用FOA对SVR的参数进行优化，首先建立关于参数(c，g)的目标函数，通过迭代算法寻找一组最优的参数(c,g)使目标函数的值最小.FOA算法主要步骤[14]为

1) 随机初始化果蝇位置：(Xaxis,Yaxis).

2) 赋予果蝇随机方向和距离：

Xi=Xaxis+RandomValue

Yi=Yaxis+RandomValue

(12)

3) 计算味道浓度判定值S.由于食物的具体位置开始无法确定，因此先估计果蝇与原点间的距离Dist，再根据Dist计算味道浓度判定值S：

(13)

Si=1/Disti

(14)

4) 求果蝇味道浓度Smell.为求出每个果蝇个体位置的味道浓度Smelli，引入味道浓度判定函数(Fitness function)，将味道浓度判定值Si带入该函数中：

Smelli=Function(Si)

(15)

5) 在果蝇群体中找出味道浓度最高的果蝇(最优个体)：

[bestSmell,bestIndex]=max(Smelli)

(16)

6) 对味道浓度值最佳的果蝇，保留其X，Y的坐标值，果蝇群体其他果蝇利用视觉飞往该位置：

Smellbest=bestSmell

(17)

Xaxis=X(bestindex)

Yaxis=Y(bestindex)

(18)

7) 进入迭代优化阶段.重复步骤2)到步骤6)判断果蝇的味道浓度是否优于上一代的味道浓度，若是则用新一代最佳浓度果蝇坐标值替换上一代的坐标值，依次直到找出最佳浓度果蝇坐标值.

2PCA-FOA-SVR模型股票价格预测

利用PCA-FOA-SVR模型对股票价格预测的流程如图2所示，具体步骤如下：

1) 选取模型训练样本，确定影响股票价格的几个因素，对样本数据进行归一化处理.

2) 对影响股票价格的因素进行主成分分析，消除冗余信息，选择主成分个数，得出主成分.确定SVR的输入、输出变量.

3) 建立目标函数，其表达式为

(19)

4) 初始化模型参数.选取SVR的核函数和参数；确定目标函数式(19)为果蝇味道浓度判定函数(Fitness function).确定果蝇优化算法的迭代次数maxgen,群体规模sizepop,算法终止的bestSmell等参数.

5) 利用果蝇优化算法对SVR的参数(c,g)迭代寻优.根据式(13，14)计算果蝇味道浓度判定值Si,将Si带入式(19)中计算果蝇味道浓度Smelli,迭代循环,寻找使目标函数最小的最优果蝇味道浓度值bestSmell.

6) 当bestSmell小于指定值或者gen=maxgen时，算法终止，取得使味道浓度值最佳的(c,g).

7) 利用最优的(c,g)建立SVR预测模型.对股票未来几天的价格进行预测.

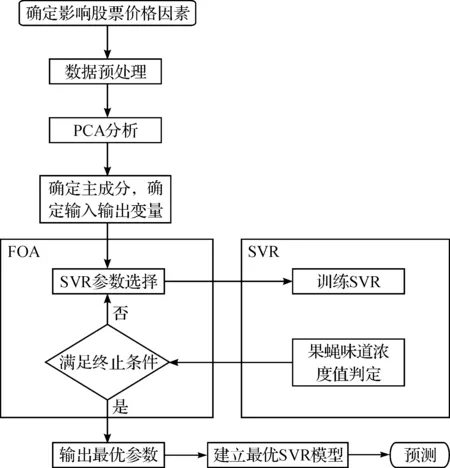
图2　PCA-FOA-SVR模型股票价格预测流程图Fig.2　The flow chart of PCA-FOA-SVR model for stock prediction

3实验仿真

3.1股票预测指标体系

选取股票宁沪高速(600377)2013年6月24日到2014年3月5日之间的交易数据为实验对象.数据分为两部分，2013年6月24日到2014年2月18日的交易数据作为训练集来构建模型，2014年2月19日到2014年3月5日的交易数据作为测试集，验证模型的有效性.选取股票的开盘价、收盘价、最高价、最低价、成交额和成交量等为影响股票价格的几个因素，作为股票价格预测模型的输入变量.股票交易数据见表1.

表1　宁沪高速股票成交信息表

为了避免原始输入变量由于量纲与数量级的不同对结果造成影响，对原始数据进行无量纲化处理，标准化公式为

(20)

3.2预测因子的PCA处理

利用SPSS软件对股票的开盘价、最高价、最低价、收盘价、成交额和成交量等6个技术指标作主成分分析，分析结果见表2.由表2可以发现前两项成分的方差累计贡献率就达到了99.056%，即保留前两个主成分即可概括原始数据的绝大部分信息.因此将主成分一和主成分二作为支持向量机的输入变量，第二天的收盘价作为输出变量.用主成分一和主成分二预测第二天的收盘价.

表2　主成分分析结果

3.3利用果蝇算法优化SVR参数

利用果蝇算法对SVR参数(c,g)进行迭代寻优，设置果蝇优化算法的最大迭代次数maxgen=100，设置群体规模sizepop=10.图3为优化过程中目标函数值随迭代次数变化情况.

图3　目标函数值随迭代次数变化情况Fig.3　Results of objective function value changes with the number of iterations

从图3中可以看到：果蝇算法在迭代初期，目标函数值就迅速下降，随着迭代次数的增加目标函数值逐渐趋向于一个稳定值，当迭代到第十八代时目标函数值已逼近算法最优值.这表明果蝇算法有着较快的收敛速度和全局寻优能力.

3.4利用SVR对股票价格进行预测

将果蝇优化算法得到的最优c和g值带入到SVR中，重新建立SVR模型对股票价格进行预测.图4为PCA-FOA-SVR模型的预测结果.

图4　PCA-FOA-SVR模型的预测结果Fig.4　Prediction results of PCA-FOA-SVR model

从图4中可以看到：PCA-FOA-SVR模型预测值的总体趋势与实际股票价格走势基本一致，模型预测值与真实值误差较小，预测效果较好.

3.5模型预测性能对比分析

为了验证模型的有效性，选取BP模型、SVR模型作为对比模型.BP神经网络的参数设置为：三层神经网络，训练次数为3 000，误差为0.001，学习率为0.005；SVR模型采用交叉验证选取最佳参数c和g.用前160个数据作为训练样本，后10个数据作为测试样本.

用误差均方根RMSE(Rootmeansquareerror)和相对误差绝对值平均MAPE(Meanabsolutepercentageerror)作为评价指标来评价模型的有效性和鲁棒性.RMSE和MAPE的定义分别为

(21)

(22)

各个模型的预测结果如表3所示.

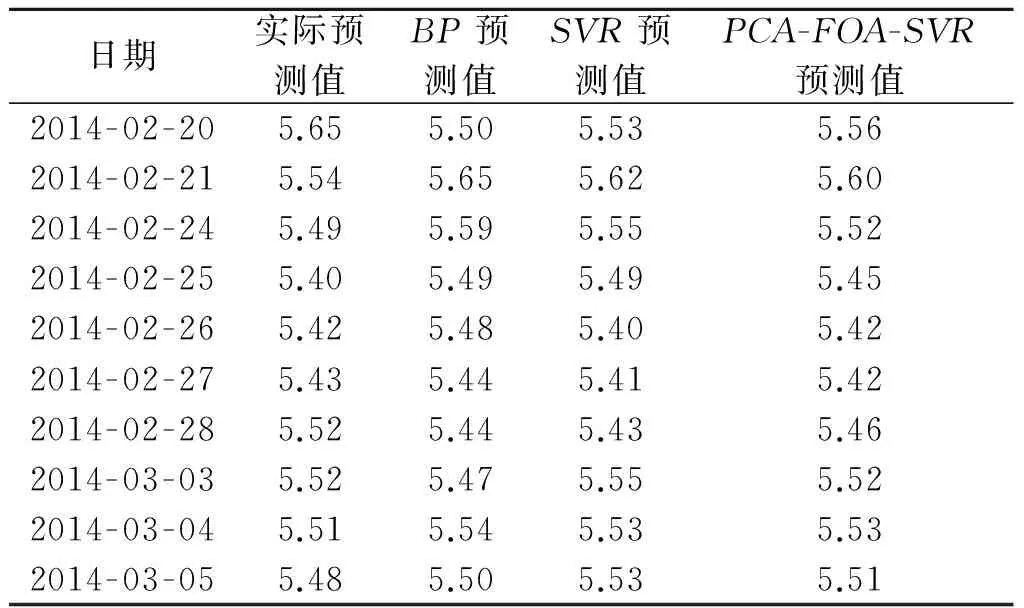
表3　各个模型预测结果

各个模型的预测误差值如表4所示.

表4　模型的预测误差

分析各个模型预测结果，由表3可知：PCA-FOA-SVR模型的预测值更接近于真实值，图5中PCA-FOA-SVR模型的走势更接近于真实曲线，与原始数据的拟合度最高.RMSE和MAPE作为衡量模型优劣的重要指标，从表4可以看出：SVR模型的预测误差低于BP模型的预测误差，PCA-FOA-SVR模型的预测误差低于SVR的预测误差，相比BP和SVR模型，PCA-FOA-SVR模型有更高的预测精度.

图5　各模型预测值对比Fig.5　Comparison results of different models

4结论

利用股票宁沪高速(600377)2013年6月24日到2014年3月5日之间的交易数据建立PCA-FOA-SVR模型，通过对影响股票价格数据进行PCA分析，将原始的6 个输入变量用两个主成分替代，消除了数据冗余，简化了网络结构，同时在SVR训练过程中加入果蝇算法，利用果蝇良好的寻优能力，解决SVR了参数难以确定的问题.实验结果表明：PCA-FOA-SVR模型相比其他模型有着更好的预测精度和泛化能力，该模型较好地反应股票价格涨跌趋势，可以为投资者提供合理有效的参考.

参考文献：

[1]冯盼,曹显兵.基于ARMA模型的股价分析与预测的实证研究[J].数学的实践与认识,2011,22:84-90.

[2]陈嶷瑛,张泽星,李文斌.基于神经网络的股票价格预测模型[J].计算机应用与软件,2014(5)：89-92.

[3]郑莉莉,黄鲜萍,梁荣华.基于支持向量机的人体姿态识别[J].浙江工业大学学报,2012,40(6):670-675.

[4]陈海英.基于支持向量机的上证指数预测和分析[J].计算机仿真,2013(1)：297-300.

[5]张世军,程国胜,蔡吉花,等.基于网络舆情支持向量机的股票价格预测研究[J].数学的实践与认识,2013,24:33-40.

[6]兰秀菊,张丽霞,鲁建厦,等.基于小波分析和PSO-SVM的控制图混合模式识别[J].浙江工业大学学报,2012,40(5)：532-536.

[7]吴景龙,杨淑霞,刘承水.基于遗传算法优化参数的支持向量机短期负荷预测方法[J].中南大学学报(自然科学版),2009(1)：180-184.

[8]PANWT.Anewfruitflyoptimizationalgorithm:takingthefinancialdistressmodelasanexample[J].Knowledge-basedsystems,2012，26(2):69-74.

[9]蔡红,陈荣耀.基于PCA-BP神经网络的股票价格预测研究[J].计算机仿真,2011(3)：365-368.

[10]李静萍.多元统计分析：原理与基于SPSS的应用[M].2版.北京:中国人民大学出版社，2015.

[11]马银晓,柳虹.因子分析法在城镇居民消费结构分析中的研究[J].浙江工业大学学报,2012,40(3)：336-339.

[12]杨杰,占君,张继传.Matlab神经网络30例[M].北京：电子工业出版社，2014.

[13]任洪娥,霍满冬.基于PSO优化的SVM预测应用研究[J].计算机应用研究,2009(3)：867-869.

[14]潘文超．果蝇最佳化演算法[M]．台北:沧海书局,2011．

(责任编辑：陈石平)

Research on stock price prediction based on PCA-FOA-SVR

WANG Weihong, ZHUO Pengyu

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Stock price prediction has been regarded as an intractable task due to the intrinsic nonlinearity and instability of stock market. In this paper, based on the traditional SVR approach, a forecasting model that integrates principal component analysis ( PCA) and fruit fly optimization algorithm (FOA) for predicting stock price was proposed. In the algorithm, in order to eliminate the redundant information, the factors which influence stock price were analyzed by PCA firstly. Second, the parameters of SVR were optimized by the fruit fly optimization algorithm. Then, with the best parameters, the SVR model was used to establish a prediction model for the nonlinearity stock price. Real data sets of stock 600377 was used for simulation experiments base on the model of PCA-FOA-SVR. Experimental results indicate that the PCA-FOA-SVR model can improve the accuracy of prediction and reduce errors. The PCA-FOA-SVR model was proved to be an effective and feasible method.

Keywords:principal component analysis; support vector regression; fruit fly optimization algorithm; stock price prediction

收稿日期：2016-01-15

基金项目：国家自然科学专项基金项目(61340058)；浙江省自然科学基金重点项目(LZ14F020001)

作者简介：王卫红(1969—)，男，浙江临海人，教授，研究方向为遥感信息提取、空间信息服务等，E-mail: wwh@zjut.edu.cn.

中图分类号：TP391

文献标志码：A

文章编号：1006-4303(2016)04-0399-06