酿酒葡萄理化指标与葡萄酒质量的灰色关联聚类分析

高　卓

(华南农业大学 珠江学院, 广东 广州　510900)

酿酒葡萄理化指标与葡萄酒质量的灰色关联聚类分析

高卓

(华南农业大学 珠江学院, 广东 广州510900)

摘要:根据灰色关联聚类分析的基本原理,结合实例说明灰色关联聚类分析方法的使用．通过对酿酒葡萄和葡萄酒进行灰色关联聚类分析,从而对酿酒葡萄进行优、良、中、差的等级划分．该方法所需原始数据少,原理简单,运算方便,易于挖掘数据规律．

关键词:灰色关联聚类; 酿酒葡萄; 等级划分

0引言

灰色关联聚类分析是灰色关联系统所包含的一种灰色关联分析方法,该方法所需原始数据少,原理简单,运算方便,易于挖掘数据规律．灰色关联聚类分析方法可弥补用数理统计方法作系统分析所导致的缺憾,对样本数量和规律性不作要求,计算量小,不会出现结果与定性分析结果相背离的情况[1]．

在我国,灰色关联聚类应用多见于对自然规律的猜测描述和探索性研究中．刘继明对大兴安岭白桦低质林土壤理化性质、土壤重金属积累情况、枯落物蓄积及持水性能、低质林生物多样性程度等低质林生态功能指标进行灰色关联聚类分析[2]．刘凤兰采用灰色关联聚类分析的方法,对山西省临汾市17个县市的农业自然资源进行了聚类评价[3]．现在越来越多的专家将灰色关联聚类分析广泛的应用于项目投资决策、经济效益分析以及环境的污染等级评定等领域．杨凡使用灰色关联聚类(粗糙近似组合决策)方法对某地房地产销售前景进行了实例分析,进而得到决策规则[4]．在对样本数据进行统计分析中,灰色关联聚类分析越来越大显身手．

1基本原理

设有n个观测对象,每个观测对象m个特征数据,得到序列如下:

X1=(x1(1),x2(2),…,x1(n)),

X2=(x2(1),x2(2),…,x2(n)),

⋮

Xm=(xm(1),x2(2),…,xm(n)),

对所有的i≤j,i,j=1,2,…,m，计算出Xi与Xj的绝对关联度ɛij得上三角矩阵

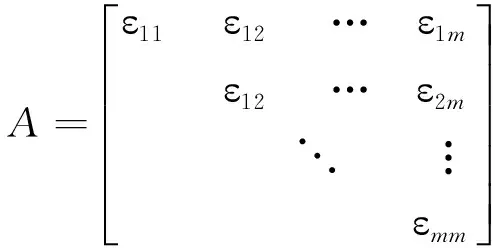
其中ɛij=1；i=1,2,…,m。取定临界值r∈[0,1],一般要求r>0.5.当ɛij≥r(i≠j)时,则视Xi与Xj为同类特征．可以根据实际问题的需要确定,r越接近于1,分类越细;r越小,分类越粗糙[6]．

2实例分析

为了进一步了解灰色关联聚类分析,本文借用2012高教社杯全国大学生数学建模竞赛A题为实例．题中第二问是要根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级．先通过主成分分析,我们可以求得:

酿酒红葡萄的主要理化指标(9个):维生素C含量(mg/L),花色苷(mg/100g)鲜重,苹果酸(g/L),柠檬酸(g/L),总酚(mmol/kg),单宁(mmol/kg),可溶性固形物(g/L),固酸比,干物质含量(g/100g)．

酿酒白葡萄的主要理化指标(10个):蛋白质(mg/100g),维生素C含量(mg/L),花色苷(mg/100g)鲜重,苹果酸(g/L),柠檬酸(g/L),总酚(mmol/kg),单宁(mmol/kg),可溶性固形物(g/L),干物质含量(g/100g),百粒质量(g)．

设酿酒红葡萄样品1～27为Wi(i=1,2,…,27);设表征任一酿酒葡萄样品的特征数为X(Si)(i=1,2,…,27)(即Wi);根据特征数的属性,得其优性数(又称为参考数)X0即max(X(Si)(i=1,2,…,27)．那么,特征数与其优性数的关联系数可用下述关系式表示:

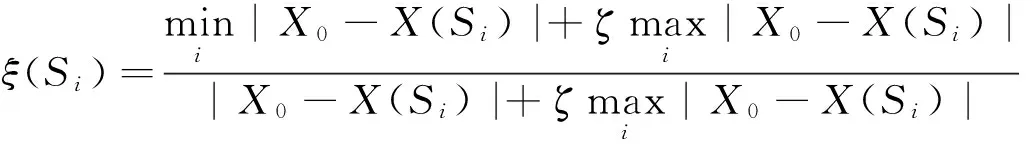
ζ为分辨系数,在0～1之间变化．传统的ζ一般取0.5,然而大量计算结果表明,0.5并不是最适合的数值,ζ的取值应遵循下述两大原则[5]:

(a) 充分体现关联度的整体性,即关联度γj不仅与X0、Xj有关,而且与其他水资源短缺因子Xk(k=1,2,…,n,k≠j)有关;

(b) 具有抗干扰作用,即当系统因子的观测序列出现异常值时,能够抑制、削弱它对关联空间的影响．

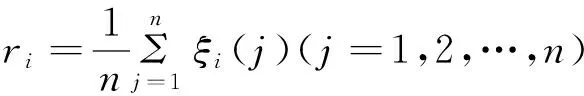
2.1灰色相似矩阵的建立

根据集R,定义各元素之间关联度差异矩阵Es为:

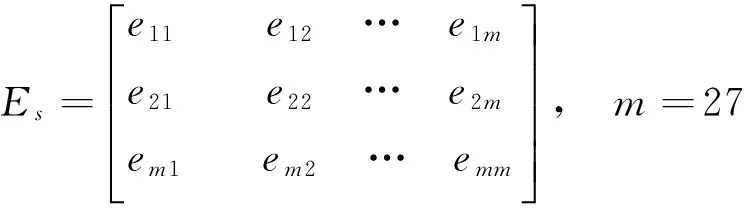
其中eij为X(Si)相对于X(Sj)的差异系数，eij=|ri-rj|/rj，Es可得差异距离矩阵Ds：

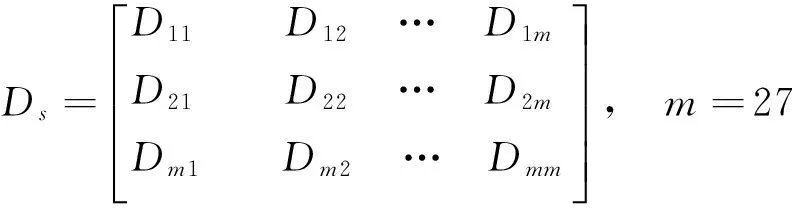
其中dji=eij+eji为差异距离,显然Es的主对角线为零,矩阵Ds是一主对角线为零的对称矩阵．由Ds可得灰色关联的相似矩阵Gs:

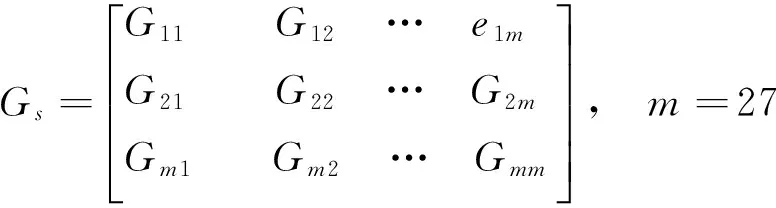
2.2聚类分析

由灰色相似矩阵Gs可得到二元数组(Si,GS),构成赋权灰色聚类图．按照(Si,GS)构造酿酒葡萄的灰色聚类图．根据所得到的灰色聚类图,任取实数λ,从权重小于λ处砍断,即得到一个不连通的灰色聚类数,其各连通部分就构成了在λ水平上的聚类．

据灰色关联聚类的原理计算,分别得到红葡萄样品和白葡萄样品的灰色关联度及排序(表1、表3)、灰色相似关系矩阵G,表1和表3中样品Wi,排序越靠前,说明该样品越接近最优,即酿酒葡萄的品质越好．灰色相似关系矩阵G给出每两样品之间相似程度．

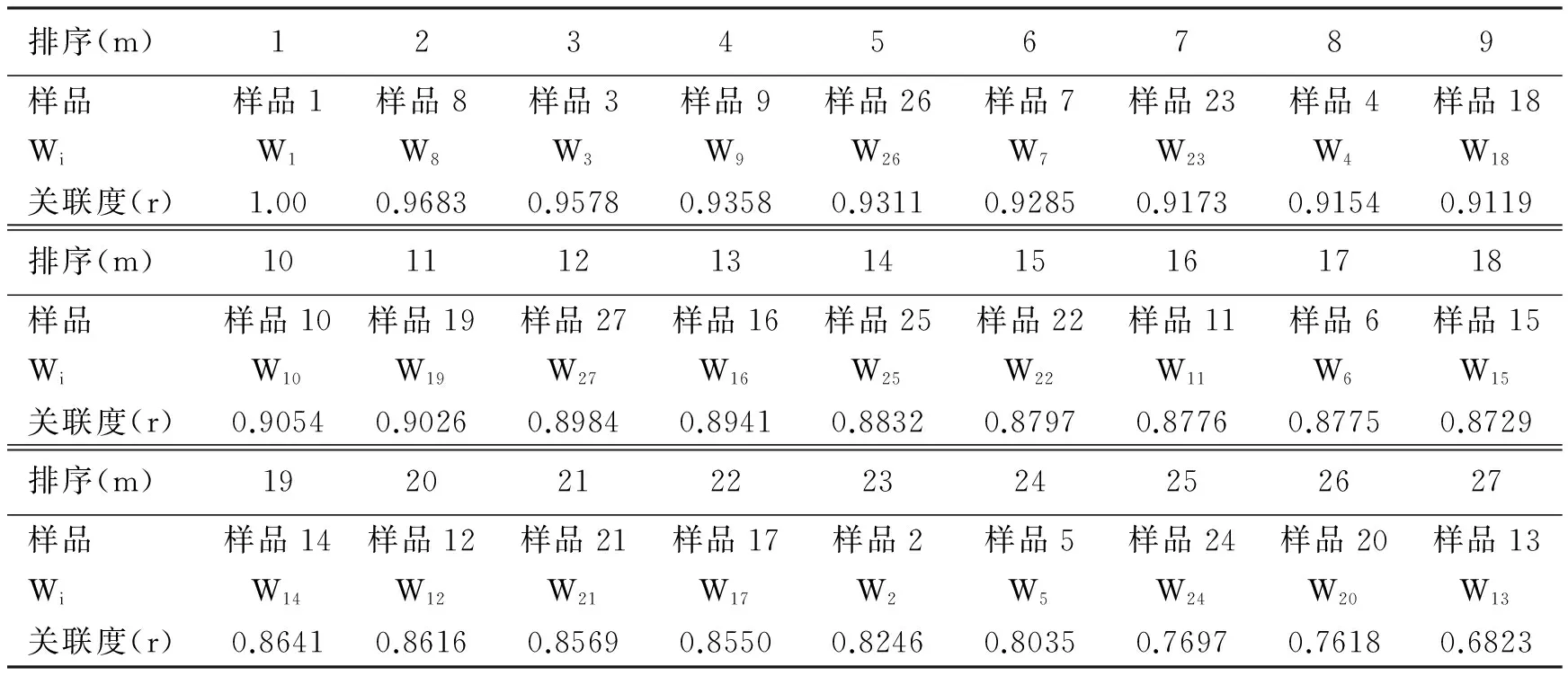
表1　红葡萄样品的灰色关联度及其排序

根据表1可求出两相邻样品之间的相关系数,取λ=0.6,且从权重小于0.6处断开,发现:λ8,3=0.5779,λ9,26=0.5152,λ20,13=0.5780,其他相关系数都是大于λ,于是酿酒红葡萄样品可划分为优、良、中、劣、差5个等级,如表2.

表2　酿酒红葡萄样品划分等级

用同样的方法即可将白葡萄分级,结果如表3.

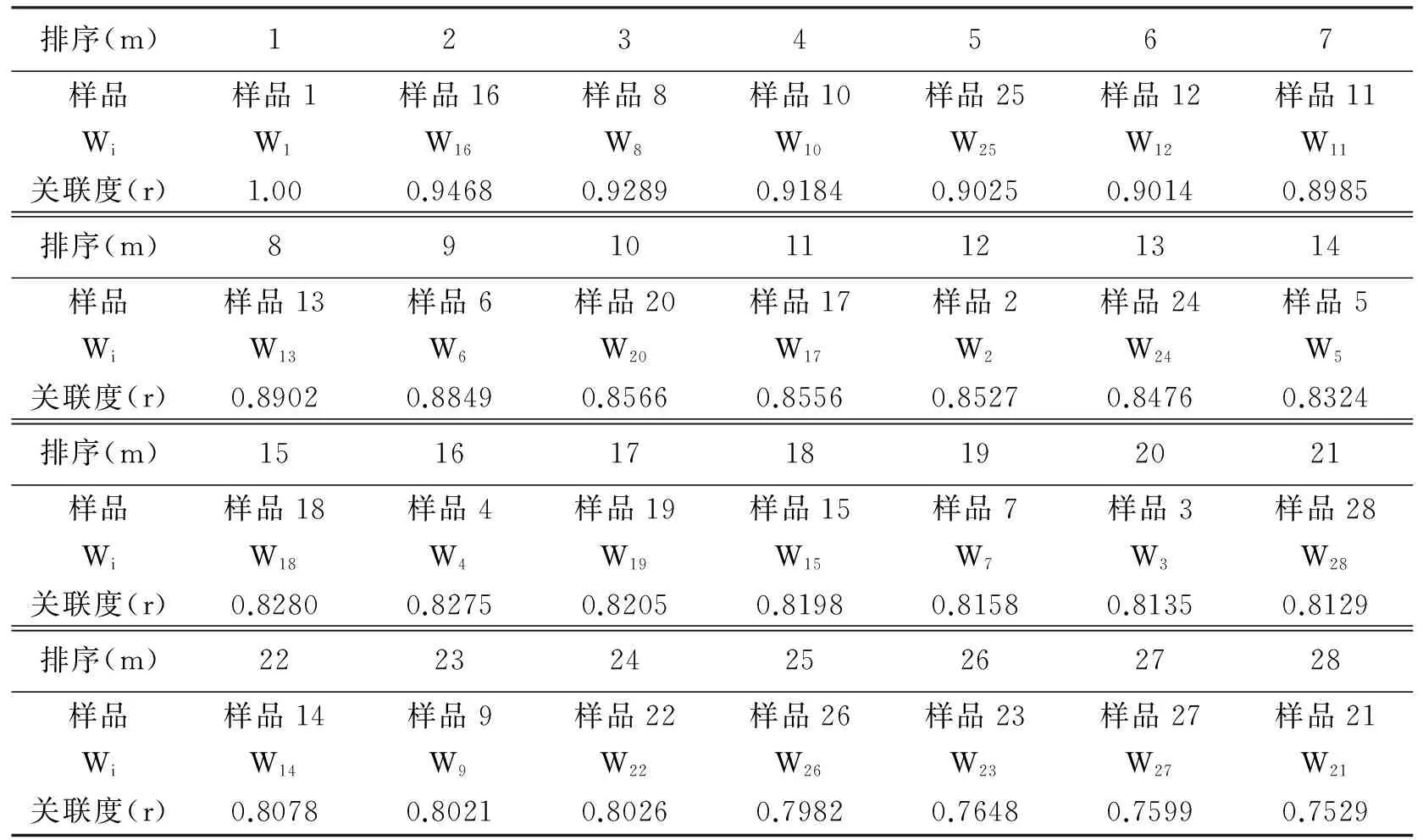
表3　白葡萄样品的灰色关联度及其排序

根据表3可求出两相邻样品之间的相关系数,取λ=0.6,且从权重小于0.6处断开,发现:λ8,10=0.5181,λ25,12=0.5277,λ27,21=0.3105,其他相关系数都是大于λ,于是酿酒白葡萄样品可划分为优、良、中、劣、差5个等级,如表4.

表4　酿酒白葡萄样品划分等级

为了简化问题,在此实例中只筛选了酿酒葡萄和葡萄酒的主要理化指标进行灰色关联聚类分析,此做法对结果的精确性会有少许影响,但还是有很高的精确性．

参考文献：

[1]鲁峰,黄金泉. 基于灰色关联聚类的特征提取算法[J].系统工程理论与实践, 2012, 32(4):873-876.

[2]刘继明,宋启亮,李芝茹,等. 大兴安岭白桦低质林生态功能评价指标的灰色关联聚类分析[J].东北林业大学学报, 2012, 40(8):112-115.

[3]刘凤兰.临汾市农业自然资源灰色关联聚类分析[J].中国农业资源与区划, 2004, 25(3):50-53.

[4]杨凡.灰色关联聚类:粗糙近似组合决策方法(GR)研究[J].南开大学学报:自然科学版, 2012, 45(5):14-18.

[5]孙晓东,胡劲松,焦玥. 基于主成分分析和灰色关联聚类分析的指标综合方法研究[J].中国管理科学, 2005(13):18-22.

[6]姜启源.数学模型[M].北京:高等教育出版社, 2001.

[责任编辑：李春红]

Gray Relation Clustering Analysis in Physical and
Chemical Indexes of Wine Grape and Wine Quality

GAO Zhuo

(Zhujiang College of South China Agricultural University, Guangzhou Guangdong 510900, China)

Abstract:This paper analyzes the basic principle, and illustrates the use of gray relation clustering with an example. The paper uses gray relation clustering Analysis in wine grapes and wine, to divide the wine grape to excellent,good,middle and bad grades.

Key words:gray relation clustering; wine grape; grade division

收稿日期:2015-12-04

基金项目:广东省高校优秀青年创新人才培养计划项目(2013LYM-0117)

通讯作者:高卓(1981-),男,讲师,硕士,研究方向为随机运筹学. E-mail: 77275491@qq.com

中图分类号:O211

文献标识码:A

文章编号:1671-6876(2016)01-0029-04