冠图Cn∘Cm的邻点可区别均匀E-全染色

魏邦魁, 强会英, 王洪申

(1.兰州交通大学 数理学院, 甘肃 兰州　730070, 2.兰州理工大学 机电工程学院, 甘肃 兰州　730050)

冠图Cn∘Cm的邻点可区别均匀E-全染色

魏邦魁1, 强会英1, 王洪申2

(1.兰州交通大学 数理学院, 甘肃 兰州730070, 2.兰州理工大学 机电工程学院, 甘肃 兰州730050)

摘要:讨论了冠图Cn∘Cm的邻点可区别均匀E-全染色,并得到了它们的邻点可区别均匀E-全色数.对简单图G, 如果图G存在一个染色法f, 使得任意两个相邻的顶点染不同的颜色; 任意一条边与其关联的点染不同的颜色;任意两个相邻的点的色集合不相同, 并且任意两色所染元素的数目之差不超过1, 则称该染色法为G的邻点可区别均匀E-全染色,其所用最少颜色数称为该图的邻点可区别均匀E-全色数.

关键词:邻点可区别均匀全染色; 邻点可区别均匀E-全染色; 邻点可区别均匀E-全色数.

0引言

图的均匀染色问题是图的染色理论中重要研究内容之一, 具有重要实际意义和理论意义,在现实生活中各个方面都有广泛应用, 比如工业生产问题中, 交通运输问题, 物资运送问题等都可以用图的均匀染色模型表示.1973 年,W.Meger提出了图的均匀点染色的概念后, 从此揭开了图的均匀染色的序幕,之后人们在图的均匀染色的概念基础上又相继提出了图的均匀边染色, 图的均匀全染色[1,2]和图的均匀邻强边染色的概念[3-5]以及张忠辅, 李刚提出的图的邻点可区别的均匀全染色的概念和猜想[6]. 本文在邻点可区别均匀全染色[7]的基础上,要求边的染色可以不正常, 讨论了图 Cn∘Cm的邻点可区别均匀E-全染色, 并得出了它们的邻点可区别均匀E-全色数.

1预备知识

定义1对于简单图G(V,E),若映射f:E(G)∪V(G)→{1,2,3,…,k}(k为正整数) 满足:

1) 对∀uv∈E(G),f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv).

2) 对∀uv∈E(G),C(u)≠C(v),其中C(u)={f(u)}∪{f(uv)|uv∈E(G)}.

3) 对∀i,j∈{1,2,3,…,k},有||Ti|-|Tj||≤1其中,Ti=Vi∪Ei,Ei={e|f(e)=i,e∈E(G)},Vi={v|f(v)=i,v∈V(G)},i=1,2,3,…,k.

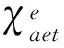
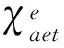
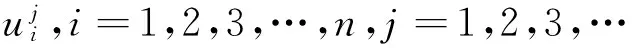
2主要结论

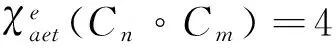
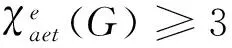
(a) 若χ(Cn∘Cm)=2,n,m≡0(mod2),时,则此时所有边只能用一色3来染,则所得各点色集合均为C={1,2,3}.故邻点不可区别.

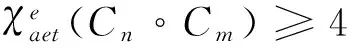
下面分4种情形讨论.

情形1当n≡0(mod2)且m≡0(mod2)时,给出Cn∘Cm的一个4-AVDEETC法,令f如

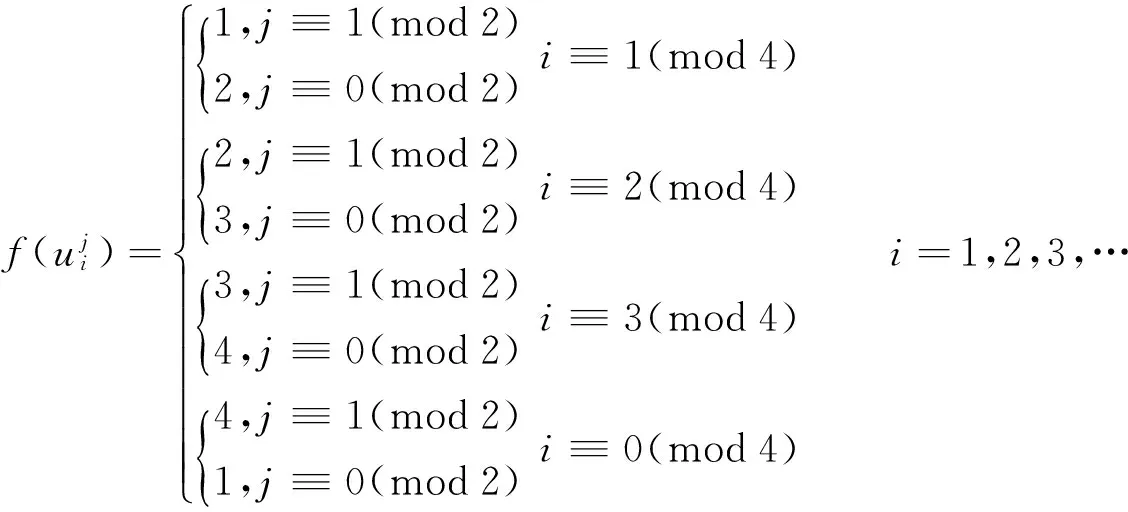
对于Cn上边的染色我们分为以下2种情形:

情形1.1当n≡0(mod4)且m≡0(mod4)时,

情形1.2当n≡2(mod4)且m≡0(mod4)时,

接下来染每个新生成的圈的边的染色情况.

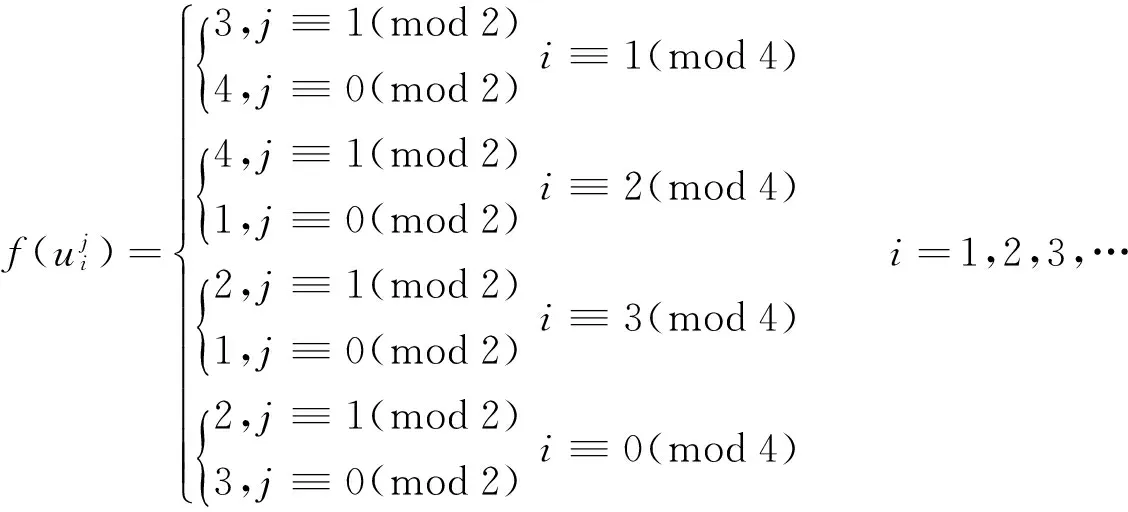
此时在情形1.1下各个点的色集合的补集.

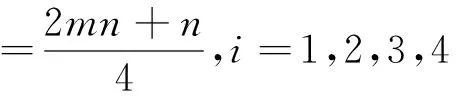
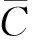
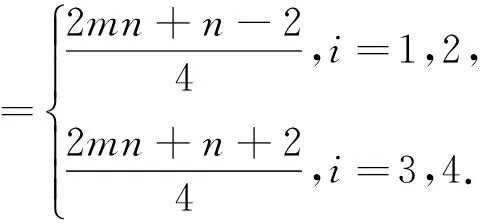
显然,在染色f下是邻点可区别的,且是均匀的.

情形2当n≡1(mod2)且m≡0(mod2)时,给出Cn∘Cm的一个4-AVDEETC法,令f如各个点的染色在情形1的基础上变化的为

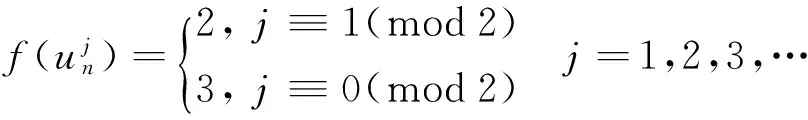
边的染色法在情形1的基础上变化的为如下:

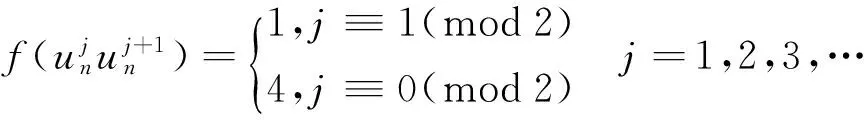
此时各个点的色集合的补集在情形1.1下各个点的色集合的补集的基础上变化的为

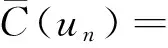
且对∀i∈C有

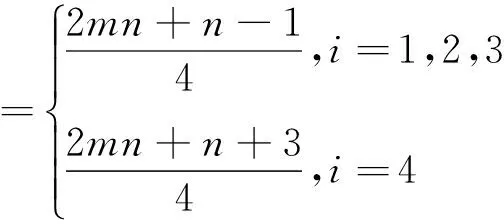
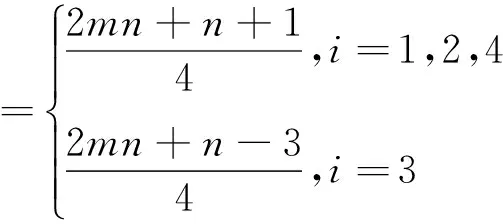
显然,在染色f下是邻点可区别的,且是均匀的.

情形3当n≡0(mod2)且m≡1(mod2)时,由于在染色中图形的元素个数不同,产生了不同的染色法,故分为如下2种情形:

情形3.1当n≡0(mod4)且m≡1(mod2)时,

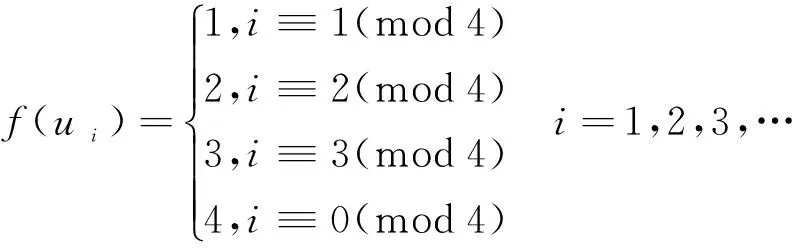
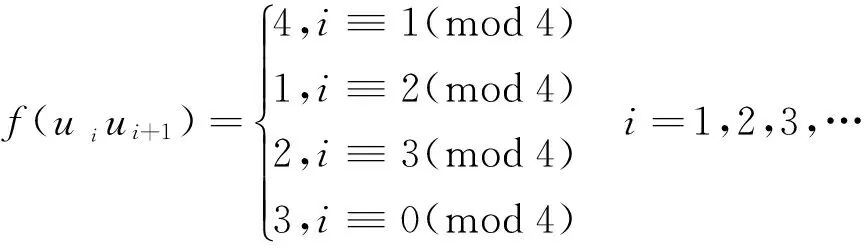
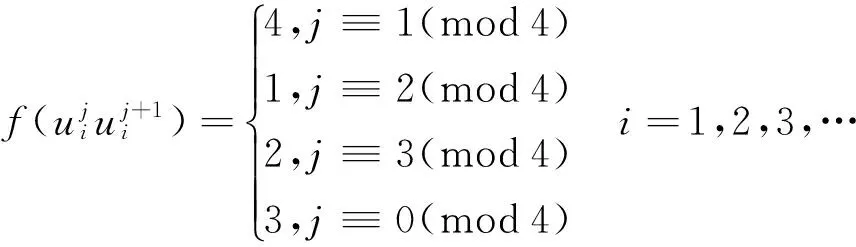
此时各个点的色集合的补集情况如下

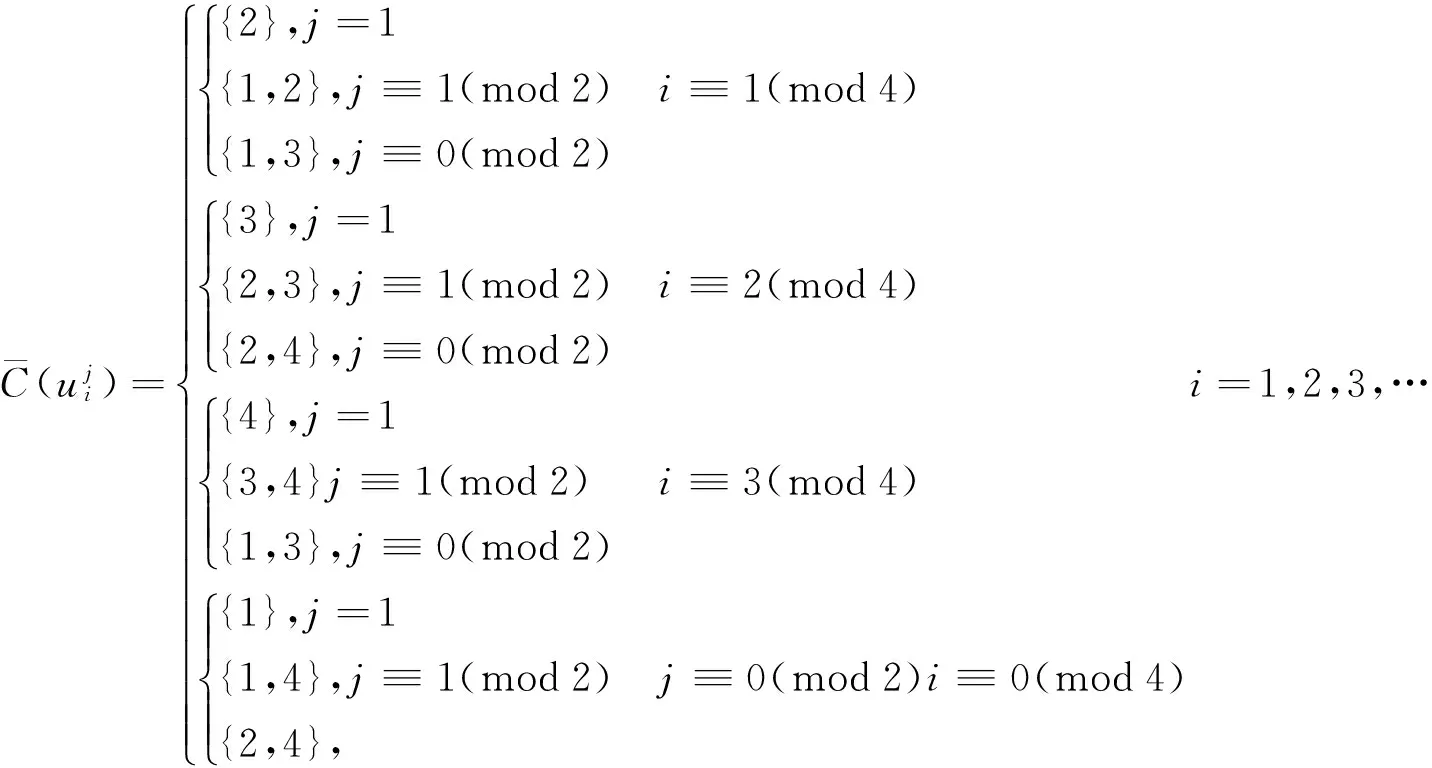
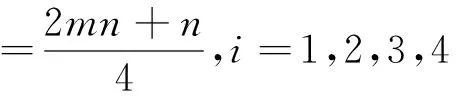
情形3.2当n≡2(mod4)且m≡1(mod2)时各个点的染色在情形3.1的基础上变化的为只要f(un-1)=1,f(un)=3,

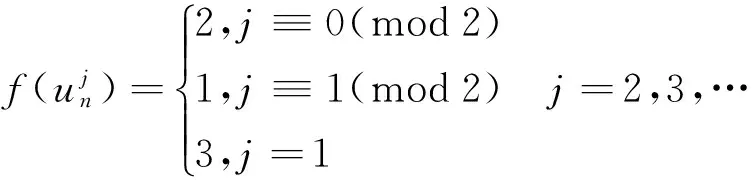
并且边的染色在情形3.1的基础上有变化的为

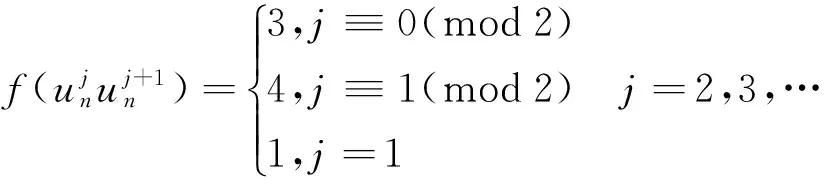
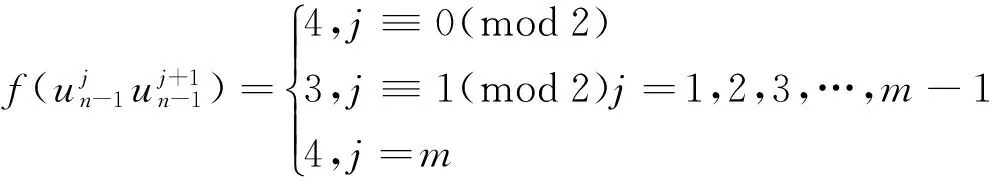
此时各个点的色集合的补集情况在情形3.1的基础上有变化的为

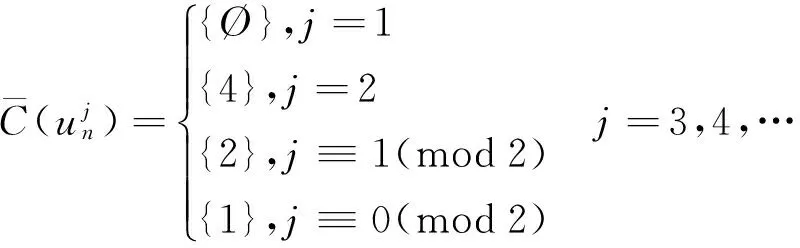
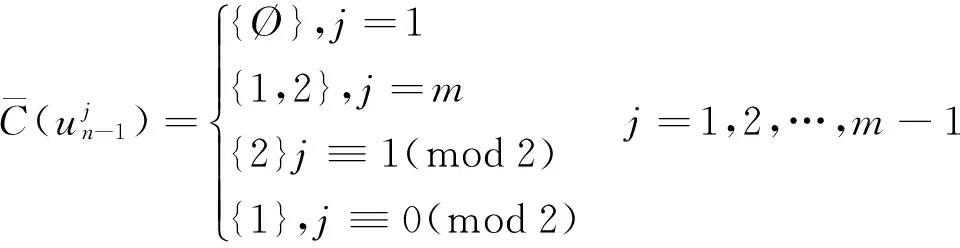
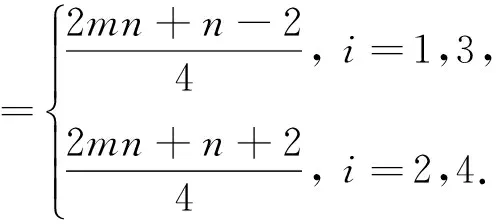
可见染色法f是邻点可区别的,且是均匀的.

情形4当n≡1(mod2)且m≡1(mod2)时,分为如下2种情形:

情形4.1当n≡3(mod4)且m≡1(mod2)时,各个点的染色在情形3.1的基础上变化的为

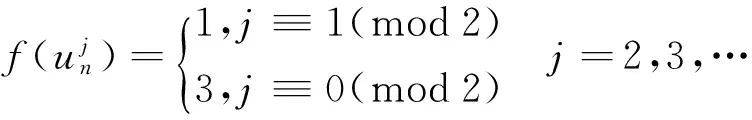
而边染色在情形3.1的基础上变化的为:

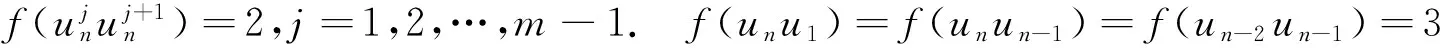
此时各个点的色集合的补集情况在情形3.1的基础上有变化的为:

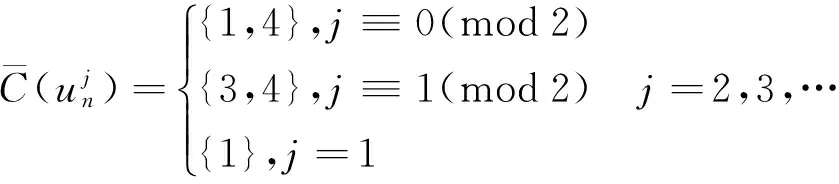
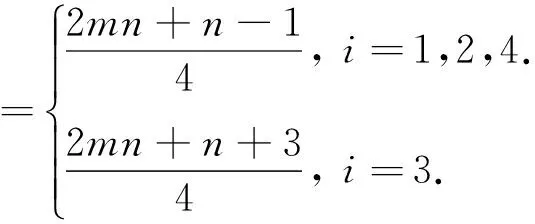
故此时的染色法也是均匀的.

情形4.2当n≡1(mod4)且m≡1(mod2)时,各个点的染色在情形4.1的基础上变化的为:

然而边染色在情形4.1的基础上变化的为:

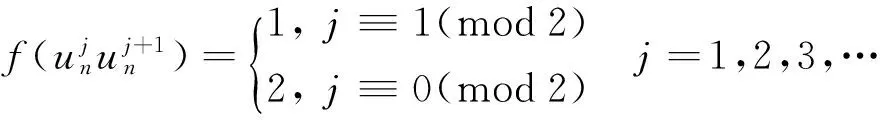
此时各个点的色集合的补集情况在情形4.1的基础上有变化的为:

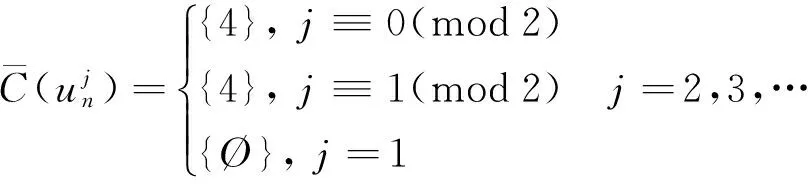
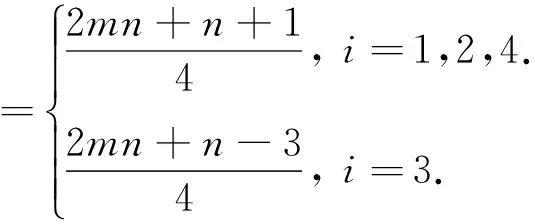
可见染色法f是邻点可区别的,且是均匀的.

由此可见,以上4种情形均已证明定理的正确性,同时也证得染法f依然是邻点可区别的,且是均匀的.从而,定理得证.

参考文献：

[1]Zhang Z F,Wang W F,Bao S,et al.On the equitabletotal coloring of some join graphs[J].Journal of Information and Computational Science, 2005(4):829-834.

[2]Wang W F.Equitable total coloring of graphs with maximum degree[J].Graphs and Combinatorics, 2002, 18(3):677-685.

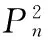
[4]Ma G,Zhang Z F.adjacent-vertex-distinguishing equitable adjacent strong Edge chromatic number of some Double Graphs[J].Pure mathematics and applied mathematics, 2010, 26(1):64-68.

[5]Zhang Z F,Li J W,Zhao C C,et al. On the Vertex Distinguishing equitable Edge chromatic number of some Join Graph[M].Acta Mathematica Sinica:Chinese series, 2007.

[6]Ma G,Zhang Z F. On Adjacent Vertex-distinguishing-equitable Total Coloring of Double Graphs[J].Journal of Jilin University (Sci Ed), 2009, 47(6):1160-1164.

[7]Zhang Z F,Chen X E,Li J W,et al. On adjacent-vertex-distinguishing Total coloring of Graphs[J].science in China Series A: Mathematics, 2004, 34(5):574-583.

[责任编辑：李春红]

The Adjacent-Vertex-Distinguishing-EquitableE-Total
Coloring of GraphCn∘Cm
WEI Bang-kui1, QIANG Hui-ying1, WANG Hong-shen2

(1.Shool of Mathematics, Lanzhou Jiaotong University, lanzhou Gansu 730070, China)

(2.School of Mechatronic Engineering, Lanzhou University of Technology, lanzhou Gansu 730070, China)

Abstract:Let G be a single graph.A total coloring f of G be called adjacent-vertex-distinguishing-equitable E-total coloring,if no two adjacent vertex of G receive same color and no edge associated with vertex assigned the same color,and for any two adjacent vertexes uand v,there must be C(v)≠C(u), what is more,the difference of the elements colored by any two colors is not more than 1.The minimal number of colors required for theadjacent-vertex-distinguishing-quitable E-total coloring of G is called the adjacent-vertex-distinguishing-equita-ble E-total chromatic numbers. In this paper, theadjacent-vertex-distingui shing-equitable E-total coloring of graph Cn∘Cmwas discussed, and the adjacent-vertex-distinguishing-equitable E-total chromatic numbers of them were obtained.

Key words:adjacent-vertex-distinguishing-equitable total coloring; adjacent-vertex-distinguishing-equitable e-total coloring; adjacent-vertex-distinguishing-equitable E-total chromaticnumbers

收稿日期:2015-12-14

基金项目:国家自然科学基金资助项目(61262045)

通讯作者:魏邦魁(1988-), 男, 甘肃兰州人, 硕士研究生, 研究方向为图论及其应用. E-mail: 13609303482@163.com

中图分类号:O157.5

文献标识码:A

文章编号:1671-6876(2016)01-0005-06