半无穷区间上一类带P-Laplacian算子微分方程m点边值问题多个正解的存在性
张 伟, 高 鹏, 张 迪
(中国矿业大学 理学院, 江苏 徐州 221116)
半无穷区间上一类带P-Laplacian算子微分方程m点边值问题多个正解的存在性
张伟, 高鹏, 张迪
(中国矿业大学 理学院, 江苏 徐州221116)
摘要:讨论了一类带P-Laplacian算子的三阶微分方程在半无穷区间上m点边值问题多个正解的存在性,运用Leggett-Williams不动点定理结合相应的格林函数,得出了存在三个正解.
关键词:m点边值问题; 半无穷区间; P-Laplacian算子; 不动点定理; 正解
0引言
无穷区间上微分方程边值问题主要起源于非线性椭圆方程的对称解和大量的物理学理论.例如:排水流量理论,不稳定的气体通过半无穷带气孔媒介问题,等离子体物理,孤立中子的电势问题等.因此,研究无穷区间上微分方程边值问题具有很大的实际意义,从而受到了很多学者的关注.由于在很多实际问题中问题的解是正解才有意义,多数文献研究正解的存在性并且所采用的方法也不尽相同.
目前人们对于整数阶微分方程边值问题解的存在性研究做出了大量的工作,并取得了很多优秀的成果.由于无穷区间上不具有紧性,从而不能直接借助于经典的Ascoli-Arzela定理来判定紧性,为了克服这一困难一些学者给出了关于无穷区间上判定相对紧的充分必要条件,使得无穷区间上微分方程边值问题得到了充分的研究.近年来,对于半无穷区间上多点边值问题的研究已经有很多优秀的研究成果[1-4].Kim[2]讨论了如下二阶微分方程在无穷区间上多点边值问题解的存在性
其中

w∈C(R+,R).
作者使用Leray-Schauder连续定理得出了解的存在性.
Jiang[3]讨论了以下带P-Laplacian算子的微分方程在无穷区间上多点边值问题解的存在性
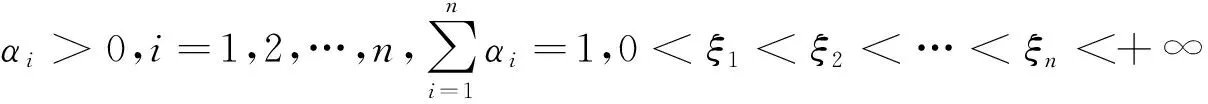
然而对于半无穷区间上三阶微分方程边值问题解的研究并不多见[5-10]. 本文考虑如下带P-Laplacian算子的三阶微分方程在半无穷区间上多点边值问题多个正解的存在性
(φp(u″))′+a(t)f(t,u)=0,0 (1) (2) (H1) f∈C[0,+∞)×[0,+∞)→[0,+∞),在[0,+∞)的任意子区间上f(t,0)≠0,且当u有界时, f(t,(1+t)u)有界; (H2) a∈C[0,+∞)→[0,+∞)在(0,+∞)的任意闭子区间上a(t)≢0,且有 本文的主要结论就是在满足以上两个条件的情况下, 运用Leggett-Williams不动点定理证明半无穷区间上边值问题(1)和(2)存在三个正解. 1预备知识及相关引理 定义1[11]设E是Banach空间,P是E中的非空闭集.如果P满足: (i) 任给x,y∈P,α≥0,β≥0,有αx+βy∈P; (ii) 若x∈P,x≠0,则-x∉P, 则称P是E中的锥. 定义2[11]设α(x)是锥P上的一个非负连续凹泛函, 如果α:P→[0,+∞)连续,并且满足 α(tx+(1-t)y)≥tα(x)+(1-t)α(y),∀x,y∈P,0≤t≤1. 定义凸集: Pc={x∈P:‖x‖ (C1) {u∈P(α,b,d):α(u)>b}≠Ø,且对u∈P(α,b,d)有α(Tu)>b; (C3) 当u∈P(α,b,c)且‖Tu‖>d时,恒有α(Tu)>b. ‖u1‖ u″(t)+y(t)=0, 0 (3) (4) 有唯一解u(t)为 其中G(t,s)=G1(t,s)+G2(t,s)且 证对式(3)两边从0到t积分两次,并注意到u(0)=0,得 (5) (6) 将式(5)代入式(6)得 从而有 因此,边值问题(3)和 (4)有唯一解为 引理2G1(t,s),G2(t,s)有如下性质: (i) G1(t,s),G2(t,s)在[0,+∞)×[0,+∞)上非负连续; (ii) G1(t,s),G2(t,s)关于变量t单调递增; 证由G1(t,s),G2(t,s)的定义,易证(i),(ii)以及(iii)当i=1时的情形. 下证,当i=2时,(iii)成立. 事实上,由G2(t,s)的定义,可得 引理3边值问题(1)和(2)等价于如下积分方程 其中G(t,s)由引理1给出. 证由引理1和边界条件(2)易得. 证由锥的定义易验证. 引理6定义积分算子T:P→E 则T:P→P. 证由注1知 注3易知边值问题(1),(2)等价于求算子T的不动点问题. 引理8假设(H1), (H2)成立,则T:P→P是全连续算子. 证由E的定义知,存在r>0,取Br=supf(t,(1+t)u),(t,u)∈[0,+∞)×[0,r],有Br<+∞,令Ω为P的任意有界子集,则 即TΩ有界. 下证TΩ在[0,+∞)的任意有限子区间上等度连续,设l>0,t1,t2∈[0,l],不失一般性,假设t2>t1,事实上, 考虑到 类似的,还有 综上可知 再证明T在无穷远处等度收敛 事实上,对任意的u∈Ω我们有 最后我们来证明T连续,取{un}∈P, un→u (n→+∞),下证Tun→Tu (n→+∞). 因此,由注2知 →0, (n→+∞). 综上可知T全连续,证毕. 2主要结果 为了方便叙述,我们给出以下两个记号 定理2假设(H1),(H2)成立,又设存在正数0 则边值问题(1)和(2)至少有三个正解,u1,u2,u3满足 ‖u1‖ 再由注2我们有 这说明定理1中的条件(C1)成立. 综上,由定理1知T至少有三个不动点u1,u2,u3使得‖u1‖ 参考文献: [1]Guo Y, Yu C, Wang J. Existence of three positive solutions form-point boundary value problems on infinite intervals[J].Nonlinear Anal, 2009, 71(3):717-722. [2]Kim C G. Solvability of multi-point boundary value problems on the half-line[J].J Nonlinear Sci Appl, 2012,5(1):27-33. [3]Jiang W. Solvability forp-Laplacian boundary value problem at resonance on the half-line[J].Boundary Value Problems, 2013(1): 1-10. [4]Zhang X. Existence of positive solutions for multi-point boundary value problems on infinite intervals in Banachspaces[J]. Appl Math Comput, 2008, 206(2): 932-941. [5]Palamides P K, Agarwal R P. An existence theorem for singular third-order boundary value problem on[0,+∞)[J].Appl M Lett, 2008, 21(12):1254-1259. [6]Shi H, Pei M, Wang L. Solvability of a third-Order Three-Pointn Bounday Value Problem on a Half-Line[J].Bull Mala Math Scie Soci, 2015, 38(3):909-926. [7]Djebali S, Saifi O. Upper and Lower Solutions forφ-Laplacian Third-order BVPs on the Half-Line[J].Cubo(Temuco), 2014, 16(1):105-116. [8]Lian H, Zhao J. Existence of unbounded solutions for a third-order boundary value problem on infinite intervals[J].Discrete Dynamics in Nature and Society, 2012(10):1-14. [9]Bai C, Li C. Unbounded upper and lower solution method for third-order boundary-value problems on the half-line[J].Electro J Dif Equ, 2009(119):1-12. [10]Agarwal R P, Jiang D. A uniqueness and existence theorem for singular third-order boundary value problem on[0,+∞)[J].Appl M Lett, 2002,15(4):445-451. [11]郭大钧,孙经先,刘兆理. 非线性常微分方程泛函方法[M]. 2版.济南:山东科学技术出版社,2006. [12]Leggett R W, Williams L R.Multiple positive fixed points of nonlinear operators on orderd Banach space[J].Indiana Univ Math J, 1979, 28(4):673-688. [13]Liu Y. Existence and unboundedness of positive solutions for singular boundary value problems on half-line[J].Appl Math Comput, 2003, 144(2):543-556. [14]Corduneanu C.Integral Equations and Stability of Feedback Systems[M]. New York: Academic Press Inc, 1973. [责任编辑:李春红] Existence of Multiple Positive Solutions for somem-point Differential ZHANG Wei, GAO Peng, ZHANG Di (Department of Mathematics, China University of Mining and Technology, Xuzhou Jiangsu 221116, China) Abstract:In this paper, we consider the existence of multiple positive solutions for a three-order m-point boundary value problems on the half line involving P-Laplacian operators. By using the Leggett-Williams fixed point theory and combined with associated Green function, we show that there exists three positive solutions. Key words:m-point boundary value problem; half-line; P-Laplacian operators; fixed point theory; positive solution 收稿日期:2015-11-25 通讯作者:张伟(1990-),男,安徽肥西人,硕士研究生,研究方向为微分方程. E-mail: 985632156@qq.com 中图分类号:O175 文献标识码:A 文章编号:1671-6876(2016)01-0011-07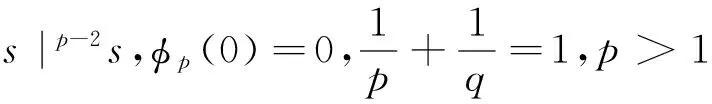
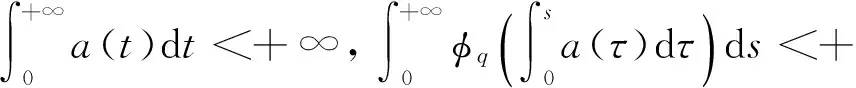
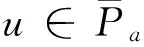
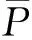
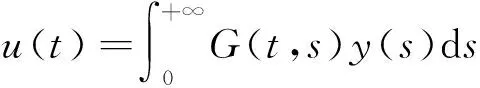
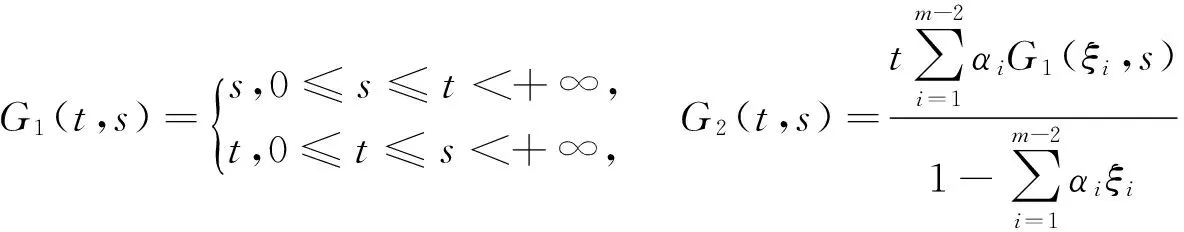
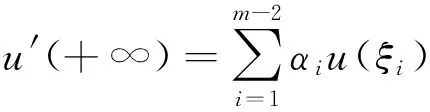



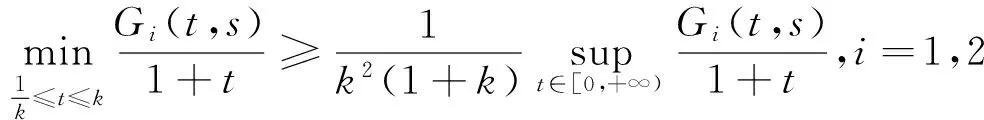

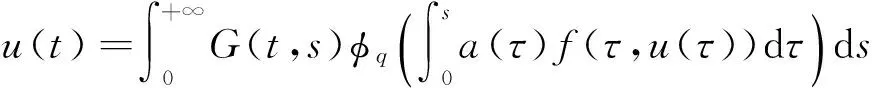
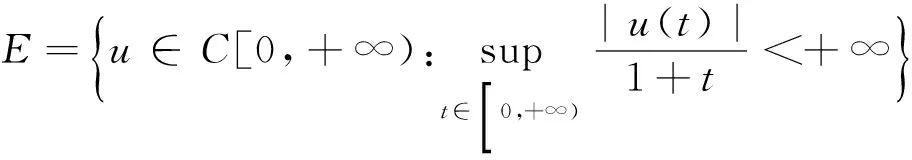

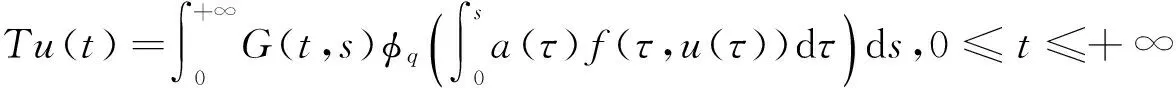

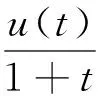
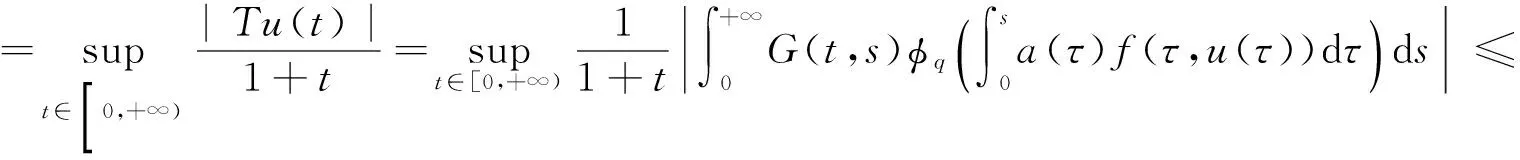



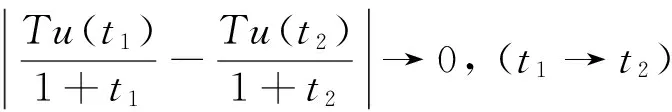
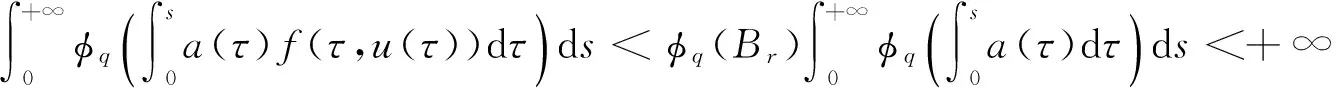


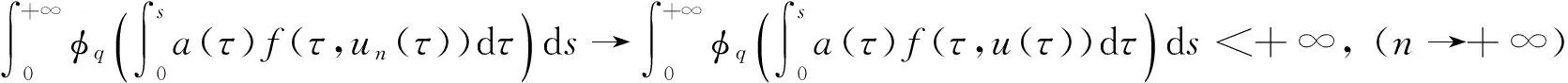

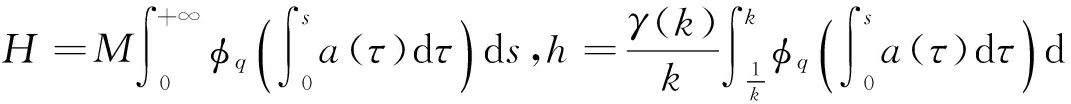
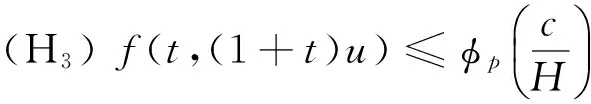
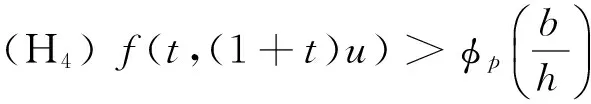
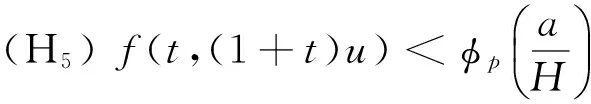
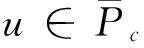
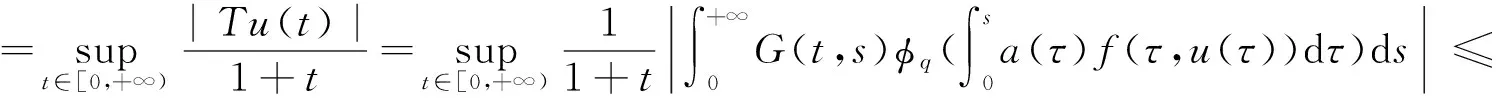
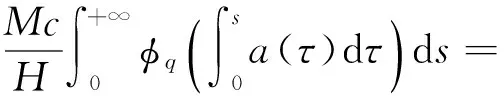
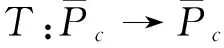
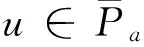
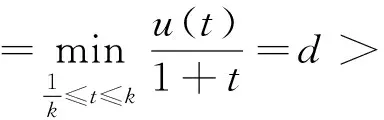
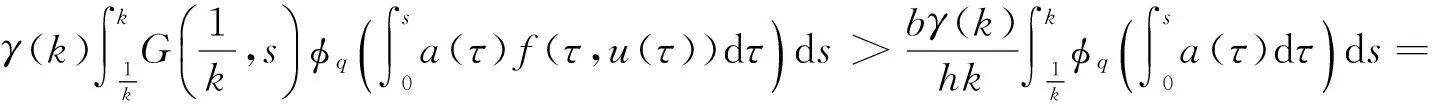

Equation InvolvingP-Laplacian Operator on the Half-line

