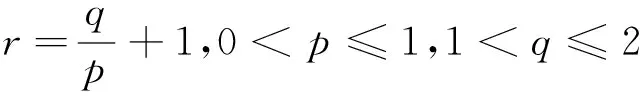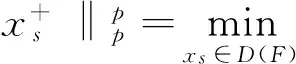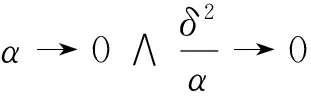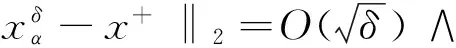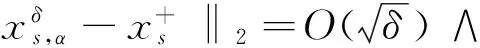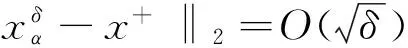稀疏约束的正则化方法

翁云华, 杜　娟

(成都理工大学 管理科学学院, 四川 成都　610059)

稀疏约束的正则化方法

翁云华, 杜娟

(成都理工大学 管理科学学院, 四川 成都610059)

摘要:给出了一个奇特的正则化方法的理论分析并用来解决(非线性)反问题,从而将正则化方法推广到稀疏域上.考察特定的Tikhonov正则化方法的稳定性和收敛性.将这种正则化方法用于传统的连续的lp空间,由于这是稀疏域上的正则化方法,所以将p限定于0到1之间.当p<1时三角不等式不再成立并且会得到一个带有非凸限制条件的伪Banach空间,证明了在传统的环境下最小值的存在性、稳定性和连续性.还给出在各自的传统假设下拓扑Hilbert空间下的收敛速度.

关键词:凸函数; 稀疏约束; 正则化; 收敛率

0引言

本文是关于在稀疏域条件下正则化方法的理论分析.我们将这种方法不妨设在 lp(p∈(0,1))空间上并且是非线性的算子.我们证明了Tikhonov正则化方法的解的存在性,解得稳定性,对数据扰动解的收敛性.除此之外,我们还将给出在各自的传统假设下拓扑Hilbert空间下的收敛速度.

考虑算子方程[2]

F(x)=y

(1)

这里F是一个非线性算子.为此我们将该式用Tikhonov方法表示,求该等式的最小值

(2)

除了传统的正则化项ψ(x),如L2范数,全部变量或者是最大正则化熵等方法,还有一个具有潜质的新奇的稀疏域上的正则化方法.

在文[1]中的几种拓展最初设定的l1正则化方法和压缩landwerber迭代是两种求最小值的算法,得到了进一步完善[6,7,9].通过文[5]中关于l1一些稀疏域上基本正则化方法的介绍我们能够实现将该方法延拓到稀疏域上.

本文主要研究了如式(2)具有良好适定性的Tikhonov正则化非线性反问题,其中ψ(x)是lp伪范数.证明了传统意义下正则化非线性算子的最小解的存在性,稳定性和收敛性.因此，用类似于求最大熵的方法将式(2)转化为在凸区域上的标准的正则化问题,此外还给出了拓扑空间标准收敛率.

1预备知识

假设X为(伪)Banach[3]空间lp(0

通常得到的yδ都是带有误差的且满足‖y-yδ‖≤δ,δ>0,这就造成了不适定问题的产生.因此关注下面广义的Tikhonov泛函

Jα:X→R

(3)

其中α>0,p∈(0,1],并且‖x‖p是lp的伪范数[4]

(4)

其中xk是数列x的第k项.

2lp-稀疏域上的正则化方法

下面所要做的事情就是将原来的泛函(3)转换成更容易得到的或者是相近的.最终改造后的最小值问题就映射成1≤q≤2区域上了,这样就能应用标准的正则化理论了,q=1时是一种特殊的情况,这时的正则化理论很多都不能成立,因此就要单独讨论.

现在xs在原式(3)中表示各个量的从属关系在当前章节中用X表示lp(0

通过特定的非线性算子,可见最小值问题成功转化,下面的定义定理可以详细说明叠加算子如何使转化成功.

定义1令φp,q是N×R到R上的映射:

φp,q:N×R

引理1[8]对任意的0

定义2定义映射序列算子Np,q，

Np,q:x|→{φp,q(k,xk)}k∈N,

x∈Z,0

显然这种方法定义的算子序列其实没什么必要,因为φp,q是不依赖于k的,但是这种方法能够清楚地看到其相近关系,从而能够更深入的了解定理定义.

命题1对任意的0

Gp,q:D(G)→Y ， x|→F∘Np,q(x) ,

问题1令yδ是真实值y的一个近似满足条件‖y-yδ‖≤δ并且α>0,最小值公式为:

(5)

映射成xs∈X,0

问题2令yδ是真实值y的一个近似满足条件‖y-yδ‖≤δ并且α>0,定义xs=Np,q(x),0

(6)

映射成x∈Z,1≤q≤2.

论点1显然问题1与问题2是等价的.

定义3假设存在一个弱非平凡拓扑,是一个正交空间,存在一个弱闭算子O使得对一切弱序

(7)

假设存在一个弱非平凡拓扑,是一个正交空间,存在一个弱连续算子O使得对一切弱序列xn有

(8)

论点2对任意的0

(Np,q(x))k=φp,q(k,xk)=sign(xk)|xk|r-1,r>1.

这种传统算子Np,q作用于lr同时有个函数:ω(t)=tr-1,根据[2]中的推论4.11以及[4]中的4.14表明Np,q是弱连续的在lr上.如:

在Z上有一个弱收敛序列,因为根据定义q≥r,能够推测出这个弱收敛序列在lr上.通过弱收敛序列在lr上,能够推出逐点收敛正如:

能够得出弱收敛序列Np,q(xn)在Z=lq上.

假设1令算子F:D(F)→Y在Z=lq,1≤q≤2上是连续的并且是弱闭的拓扑结构.

假设2当0

(9)

(10)

基于SIP管理模块的BIM技术在装饰工程项目管理中的应用……………………………………………………… 魏忠（10-269）

‖(xs)n-xδ‖p→0

(11)

通过引理2可以推断出原始变量的收敛率.但是最小的延伸引理将另外处理提供收敛对原始拓扑X,0

3收敛速率

通过使用局部利普希茨连续性,定义1中可以直接推断原始变量在拓扑Z=lq,1

(12)

令yδ测量数据满足‖y-yδ‖≤δ,α>0

(13)

定理400,再令算子F:D(F)←Y是满的,y∈Y是最小解存在的条件.令yδ测量数据满足‖y-yδ‖≤δ,α>0,如下性质成立:

1) 算子F是可微的

2) 存在ω∈Y使得如下式子成立

‖(F∘Np,q)′(x)-(F∘Np,q)′(x+)‖β‖x-x+‖2

3) 存在β>0使得β‖ω‖<1成立.则

(14)

从而

(15)

由式(13)关于原始变量的收敛率以及φp的局部利普希茨连续性可得

(16)

由此得到了常见的假设在稀疏的背景下促进正规化收敛率.

4结论

以上方法利用一个众所周知的结果在希尔伯特空间拓扑下的经典假设.证明了最小解的存在性,稳定性,连续性和Tikhonov正则化方法的延拓:

Jα:X→R

在序列空间中的收敛性.为此更改给定的问题经典配方,利用正规化理论的结果，最终得到了正则化解的收敛速度,为求Tikhonov正则化解提供了一般方法.

参考文献：

[1]Bonnans J F, Shapiro A. Perturbation analysis of optimization problems[M]. Operations Research:Springer, 2000.

[2]Caillau J B, Noailles J. Sensitivity analysis for time optimal orbit transfer[J]. A Journal of Mathematical Programming and Operations Research, 2013, 49(4): 327-350.

[3]Castillo E, Conejo A, Pedregal P, et al. Building and solving mathematical programming models in engineering and science[M]. Taylor & Francis:Lie Transactions, 2009, 35(9):918-919.

[4]Conejo A, Castillo E, Mínguez R, et al. Decomposition Techniques in Mathematical Programming Engineering and Science Applications[M].ResearchGate:Springer Berlin, 2011.

[5]Gelfand I M, Fomin S V. Calculus of Variations[M].ResearchGate:Progress in Nonlinear Differential Equations & Their Applications, 1963.

[6]老大中. 变分法基础[M]. 北京:国防工业出版社, 2004.

[7]Castillo E, Conejo A J, Castillo C,et al. Perturbation approach to sensitivity analysis in mathematical programming[J]. ResearchGate,Optim Theory and Applications, 2006, 128(1):49-74

[8]Castillo E, Conejo A, Castillo C. A closed formula for local sensitivity analysis in mathematical programming[J]. Taylor & Francis,Engineering Optimization, 2006(38): 93-112.

[9]Gal T, Greenberg H J. Advances in Sensitivity Analysis and Parametric Programming[M]. Springer:Kluwer Academic Public, 1997.

[责任编辑：李春红]

The Sparse Convex Constrained Regularization Method

WENG Yun-hua, DU Juan

(College of Management Science, Chengdu University of Technology, Chengdu Sichuan 610059, China)

Abstract:This paper presents a peculiar regularization method of theoretical analysis is used to solve the inverse problem of (nonlinear) so as to promote the regularization method to the sparse domain.We look at specific Tikhonov regularization method of stability and convergence.We are going to the regularization method is used in the traditional continuous lpspace,So we will be limited p between 0 to 1,while p<1,Triangle inequality is no longer set up and we'll get a pseudo Banach space with non convex constraints.We are going to prove the existence of the minimum value in the traditional environment, the stability and continuity.In addition, we will also be given in the respective topological Hilbert space under the traditional assumptions of the convergence speed.

Key words:convex function; sparse constraints; regularization; convergence rate

收稿日期:2015-11-24

通讯作者:翁云华(1991-)，男，四川宜宾人，硕士研究生，研究方向为应用泛函分析. E-mail: 1123068138@qq.com

中图分类号:O29

文献标识码:A

文章编号:1671-6876(2016)01-0024-05