空间绳网二级发射模式动力学分析

高庆玉，唐乾刚，张青斌，丰志伟（国防科学技术大学航天科学与工程学院，湖南长沙410073）



空间绳网二级发射模式动力学分析

高庆玉，唐乾刚，张青斌，丰志伟
（国防科学技术大学航天科学与工程学院，湖南长沙410073）

摘要：借鉴降落伞“先拉出、后展开”思想，提出一种空间绳网二级发射模式，并建立了数值仿真模型。该发射模式将绳网拉出展开过程分解为拉出和展开两个步骤，进行分步控制，保证了绳网规则、有序地拉出，避免了绳网拉出展开过程中的缠绕、穿透和打结等问题。将数值仿真结果与地面试验数据进行对比，验证了该模型的有效性和可用性。空间绳网二级发射模式的提出与仿真模型的建立为空间绳网发射优化设计提供了一种参考途径。

关键词：飞行器发射与回收、飞行技术；空间绳网；动力学建模；二级发射；数值仿真；优化设计

高庆玉（1985—），男，博士研究生。E-mail：gao. qing. yu@163. com

0 引言

空间绳网技术利用柔性绳网捕获目标的方法回收废弃的航天器及碎片，是伴随着空间技术的发展而出现的一项新技术［1］。目前欧洲太空局［2 -3］、美国［4］、英国［5 -7］、日本［8 -9］以及国内的一些研究机构［10 -13］正在积极开展相关方面的研究。虽然关于空间绳网的公开资料十分有限，但是可知某些相关支撑技术（如空间绳系动力学、材料和释放控制技术）已经通过了空间飞行试验考核。对于绳网发射展开程序方法，目前所公布的技术资料中主要提及以下两种模式：

1）发射准备前，绳网收纳于可旋转轴内部，4个顶点分别与质量块相连接。动量轮加速中心转轴及质量块，在一定的旋转速度下释放质量块，绳网在质量块离心力的作用下实现旋转展开，称之为旋转展开模式［6］。

2）发射准备前，绳网折叠收纳于网舱内，4个顶点分别与质量块相连接。发射器点火后，火药推动质量块以特定的角度、速度发射，绳网在质量块的牵引下完成抛射过程，并逐步展开。绳网发射展开仅由一次发射即可完成绳网的拉出展开，称之为一级发射模式［12 -16］。

目前旋转展开模式在国外尚处在起步阶段，技术相对复杂，对系统结构设计技术以及相关控制技术要求高，国内鲜有涉及。国内研究多采用一级发射模式，但在这种发射模式下，发射过程中网体接触面积大、质量块速度高，容易发生缠绕、穿透和打结等现象。

本文借鉴降落伞“先拉出、后展开”思想，针对空间绳网抓捕系统提出一种二级发射模式，并采用离散化的建模思路建立了系统的多体系统动力学模型，通过试验对比验证模型的有效性；对二级发射模式下的发射参数对绳网展开性能的影响进行了研究。

1 空间绳网二级发射模式

空间绳网的发射过程与降落伞的开伞过程具有一定相似性，但由于涉及穿透现象，问题更为复杂。降落伞的开伞过程按时序可分为拉直阶段和充气阶段，通过按时序分阶段控制提高了系统的可靠性和有效性，目前技术已经趋于成熟。本文借鉴降落伞的这种“先拉出后展开”思想提出了空间绳网的二级发射模式。

1. 1 系统组成

如图1所示，空间绳网二级发射展开装置由网舱、网舱盖、一级发射装置、二级发射装置、质量块（4个）组成。

1. 2 工作过程

二级展开模式下绳网的展开过程分为一级拉出和二级展开两个过程。

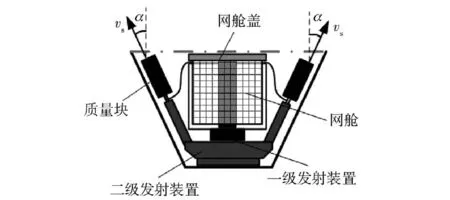
图1 空间绳网二级发射装置Fig. 1 Two-stage projection mechanism of space nets

空间绳网的一级拉出过程如图2所示。网舱盖在一级发射装置的作用下获得弹射速度υf，实现弹射分离。网包随网舱盖弹出，绳网在网舱盖的带动下从网包内依次“倒序”拉出。

图2 一级拉出过程Fig. 2 The first-stage of outstretching course

空间绳网的二级展开过程如图3所示。在绳网拉直到设定延时点火长度Ls瞬间，二级发射装置点火推动4个质量块按照设计发射速度υs、发射张角α运动（发射张角α定义为质量块速度方向与网舱轴线间的夹角，如图1所示）。在质量块的牵引下，绳网由后向前逐步展开，并最终达到张满状态。

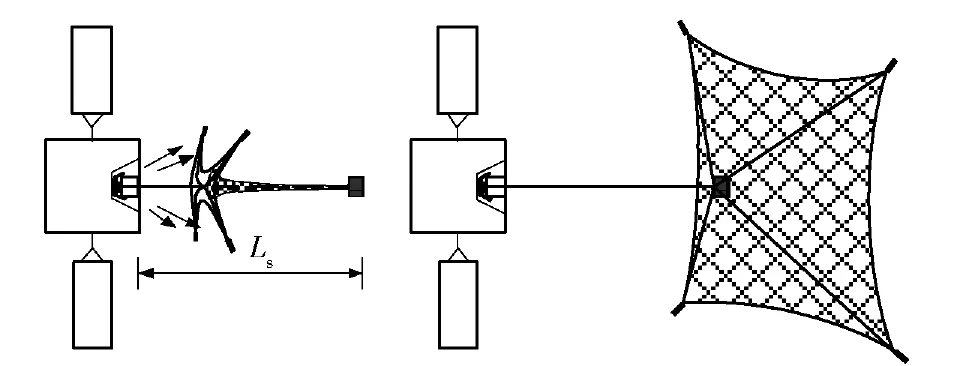
图3 二级展开过程Fig. 3 The second stage of opening course

经过大量地面试验验证发现，无论是一级发射模式还是二级发射模式，绳网间的摩擦纠缠都无法完全避免，具有一定的不确定性。但二级发射模式将绳网拉出展开过程分离为拉出和展开两个步骤，进行分步控制，保证了绳网规则、有序拉出，减弱了绳网拉出展开过程中的缠绕、穿透和打结等问题。

2 动力学模型

以集中质量阻尼弹簧方法［1，16］为基础，在一定假设的前提下，建立空间绳网二级拉出模式的动力学模型。模型分为一级拉出模型和二级展开模型两个部分。

2. 1 一级拉出模型

2. 1. 1 模型假设

在绳网一级拉出过程中，每一绳网束连续地从网包内拉出，未拉出的所有绳网固定在网包内，与网包和网舱盖一起运动。为便于建立模型，进一步做如下假设：

1）网束从顶点到底端质量均匀增加；

2）网束拉出过程中，拉出中心点位置保持不变；

3）网束从网包内按序逐段拉出，不存在两段或多段同时拉出，即不存在所谓突然“抖出”现象。

如图4所示，在上述假设前提下，将已拉出的网束划分为n个节点，n -1个绳段。每个绳段处理为质量集中在两端节点上的阻尼弹簧，节点i的质量记为mi，连接节点i、j的绳段单元记为sij.

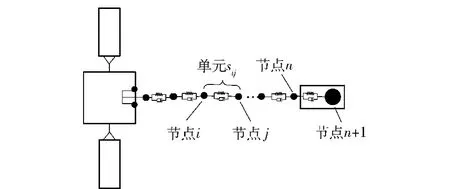
图4 拉出过程的离散化模型Fig. 4 Discretization model of outstretching course

空间绳网系统简化为由已拉出的网束单元sij、正在拉出的网束节点n以及网舱盖节点n +1组成的多体系统。

2. 1. 2 已拉出节点动力学方程

已拉出绳段节点的运动由相应绳段上的绳索张力、气动阻力和重力来决定。

绳段单元sij的绳索张力Tij近似为线弹性与线性阻尼之和，可由（1）式进行计算：

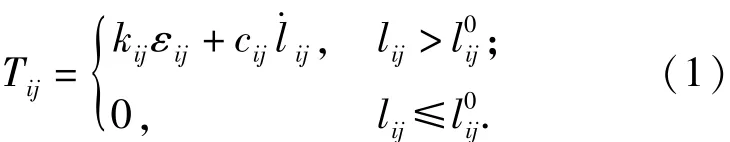
如图5所示，在惯性系下节点i、j的位置矢量分别为r、r，则绳段s的实际长度l及其变化率为

ijijij

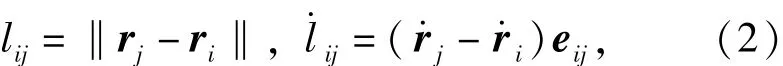
式中：eij为由节点i指向节点j的单位矢量，即

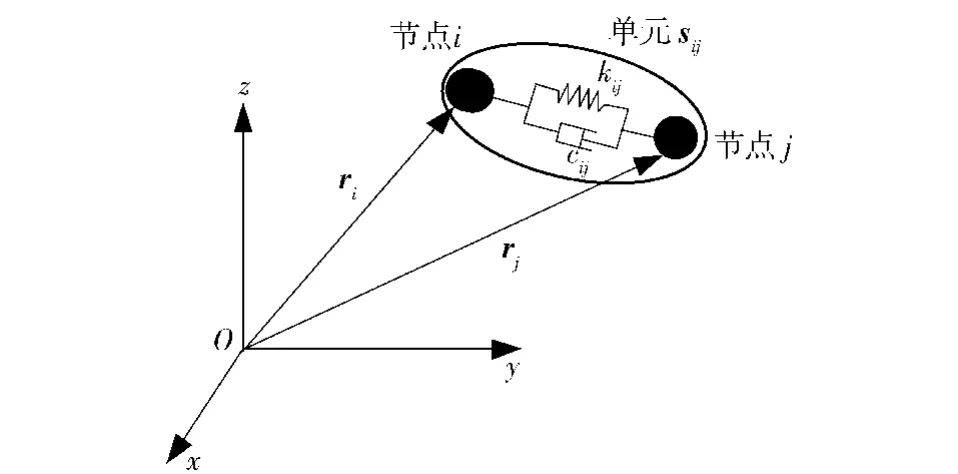
图5 绳段单元质量阻尼弹簧模型Fig. 5 Semi-spring damper model of tether segment

绳段sij的等效弹性系数kij为

式中：E为杨氏模量，由材料属性决定；Aij为绳段sij的横截面积。

绳段sij的等效阻尼系数cij为

式中：mij为绳段sij的质量；ζ为绳索阻尼比，该参数取决于绳索的材料和编织方式。

作用于绳段的外力主要包括重力和气动力，气动力可以分解为气动阻力和气动升力，如图6所示。作用于绳段sij的外力F为

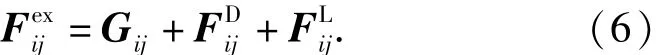
图6 地面环境下作用于sij的外力Fig. 6 Aerodynamic force applying on cable

设地面重力加速度为g，方向竖直向下，则重力Gij可表示为

式中：ρlij为sij的线密度。

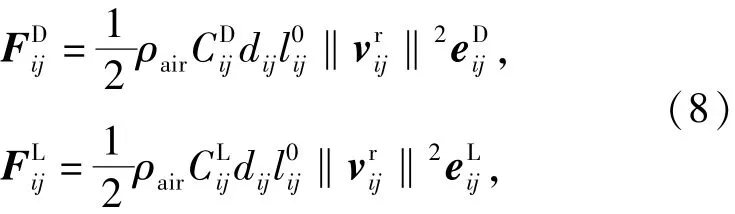
式中：ρair为大气密度；dij为绳段的直径；v为绳段相对于风的速度，设地面风速为vwind，则

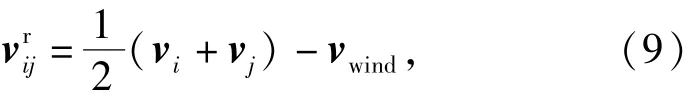
vi和vj分别为节点i和节点j的速度；e为气动阻力方向单位矢量，与方向相反；e为气动升力方向单位矢量，有

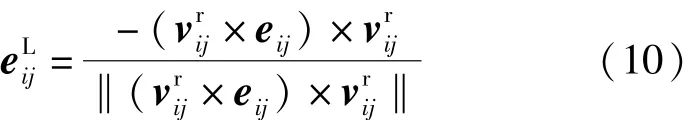
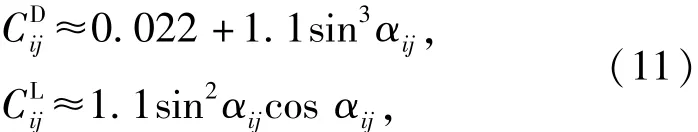
αij为sij的攻角。

定义conn｛i｝为共用节点i的所有单元的集合，在地心惯性系下，已拉出绳段节点i的动力学方程可以表示为

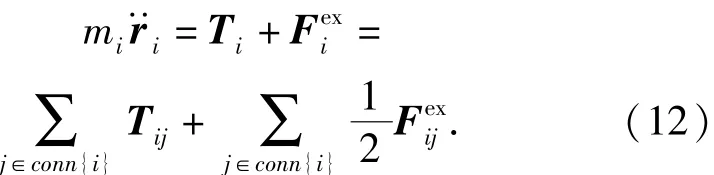
2. 1. 3 正在拉出绳网束结点的动力学方程

正在拉出的网束采用变质量动力学模型，以避免拉出过程中绳网束张力的剧烈波动。如图4所示，在模型中认为正在拉出绳段的质量集中在第n个绳段结点上，即第n个结点是变质量点。则其动力学方程具有如下形式：

式中：Tn -1，n、F分别可有（1）式和（6）式求得；F可将（6）式～（8）式中的绳段自然长度替换为绳段拉出长度ln，n +1求得；Tn，n +1可根据动量守恒定律表示为

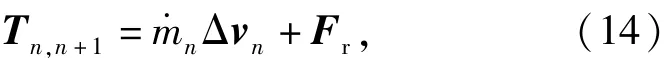
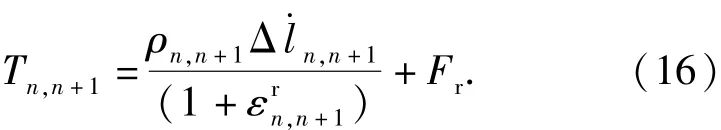
2. 1. 4 网舱盖的动力学方程

在本模型中网舱盖、网包以及未拉出的绳段一起运动，将其质量记为mn +1.则其动力学方程为

式中：vb为网舱盖的速度；Qn +1为网舱盖的气动力。

联立由（12）式、（13）式和（17）式得到空间绳网拉出过程中的多体系统动力学方程组。

初始时刻，所有绳网束节点及网舱盖节点重合于坐标（0，0，0）点，网束第1节点与网舱固连，网舱盖及网包内的绳网节点获得非零常值初始速度v0b.对方程组进行数值求解即可得到空间绳网拉出过程中各节点的运动状态。

2. 2 二级展开模型

如图7所示，对于二级展开过程采用离散化的建模思路［12］，将绳索单元处理为质量阻尼弹簧单元，绳网则简化为通过绳索单元连接的多体系统动力学模型。在建模过程中，首先计算各单元张力，再计算各单元所受外力，然后将其等效到关联节点上；最后联立各节点动力学方程，得到绳网系统的动力学方程。方程的初始边界条件由一级拉出方程的计算结果映射得到。

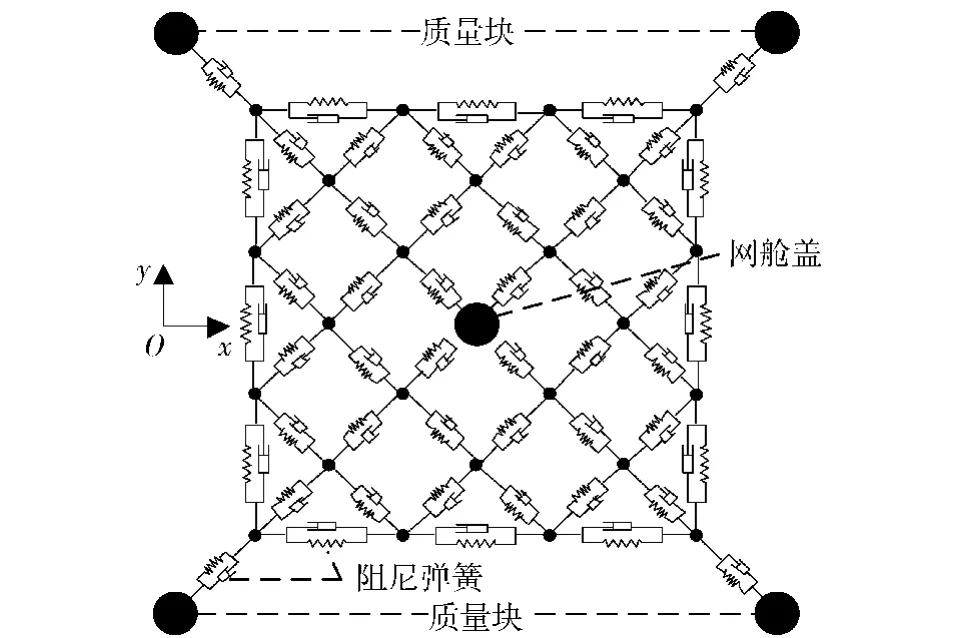
图7 绳网多体系统示意图Fig. 7 Multibody system model of flexible net

2.2.1 基本假设

绳网二级展开动力学模型的基本假设如下：

1）绳索可拉不可压，有纵向的弹性和阻尼；

2）忽略绳索结构中的弯曲挠性。

2. 2. 2 网格离散

设L为绳网边长，Nd为正方形绳网每条边划分的段数，Lmesh为网目尺寸，则对于四边形菱型网，有

设N为绳网划分的总节点数，则对于正方形网目的绳网，有

设Ns为绳网划分的总绳段数，则对于正方形网目的绳网，有

假设绳段的质量集中均分于两端点，则节点的质量等于与之相邻的绳段的质量之和的一半。节点i的质量mi为

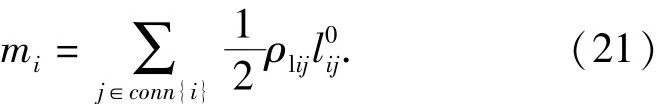
另外，对于4个质量块节点，还需在（21）式右侧加上质量块的质量ms.

2. 2. 3 系统节点动力学方程

节点内力为绳段中的张力，将绳段单元等效为“半弹簧阻尼”单元，绳段中的张力由（1）式计算得到。

节点外力包括重力和气动力，分别由（7）式和（8）式计算得到。

求得节点内力和外力后得到系统动力学方程，具体形式见（12）式。

2. 2. 4 初始边界条件传递

二级展开模型中各节点的初始位置和速度的x、y向分量由网格离散得到，z向分量由一级拉出模型的计算结果映射得到。

设由一级拉出过程结束时计算得到的网束节点位置和速度的z向分量分别为r和，二级展开模型中各节点的初始位置和速度的z向分量分别为r和，则在如图8所示的映射点上满足如下关系：

3 地面试验与仿真

为验证空间绳网二级拉出模式及其动力学模型，设计并开展了空间绳网地面试验。试验针对一级发射模式和二级发射模式分别建立了两种试验工况。

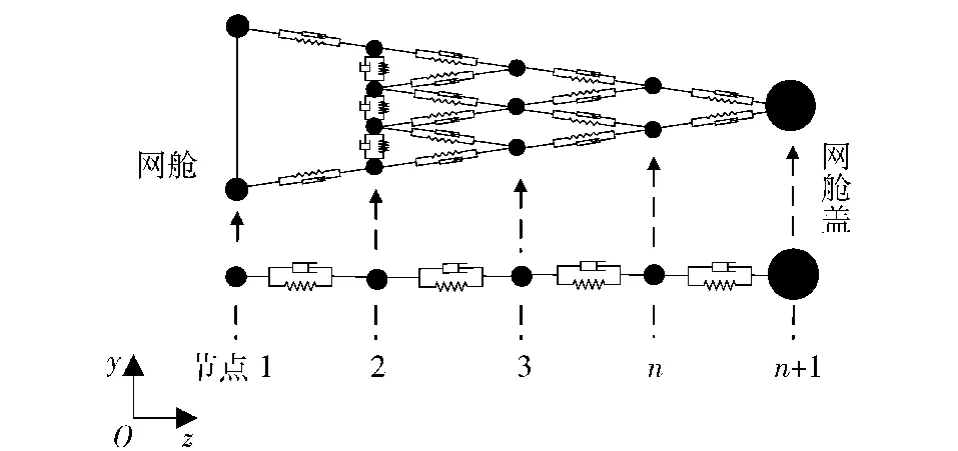
图8 节点位移与速度信息的传递示意图Fig. 8 Node displacement and transfer of velocity information

地面试验采取垂直向下发射方式。绳网采用40 m×40 m正方形菱形网（绳网构型参考图7），设计面积（平铺状态）为1 600 m2，网目边长为0. 4 m.

绳网材料选取如表1所示。绳网质量为3.6 kg，网舱盖质量为0. 5 kg，4个质量块质量均为1. 5 kg.

表1 绳网材料Tab. 1 Material of space net

一级发射模式下，4个质量块的发射速度为25 m/ s，发射张角为55°；二级发射模式下，一级发射速度υf=3 m/ s，延时点火长度Ls= 27 m，二级发射速度υs=25 m/ s，二级发射角度α=55°.

根据上述试验工况，利用FORTRAN语言编程建立了空间绳网的两种发射模式下的动力学模型，进行了仿真计算。

图9所示为二级模式下绳网完成一级拉出后继续进行二级展开的位型图。

定义绳网的展开面积为飞网网口在发射方向的投影面积，描述了飞网的实际覆盖范围，决定了飞网可捕获目标的尺寸。由于试验数据仅跟踪质量块的运行轨迹，故采用简化（23）式计算展开面积：

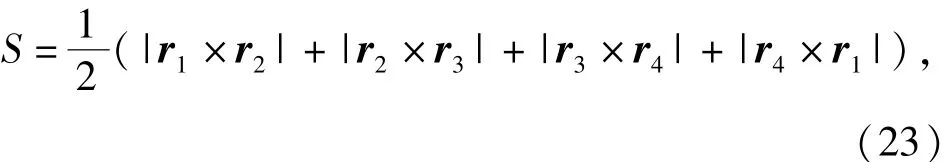
式中：r代表质量块位移矢径在垂直飞网发射方向上的投影；下标代表质量块沿同一方向的顺序编号。

定义绳网的飞行距离为飞网4个质量块在飞网发射方向上的飞行距离，由（24）式计算：

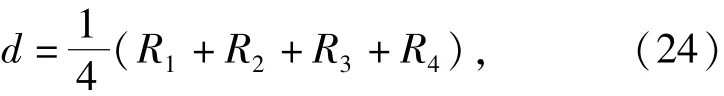
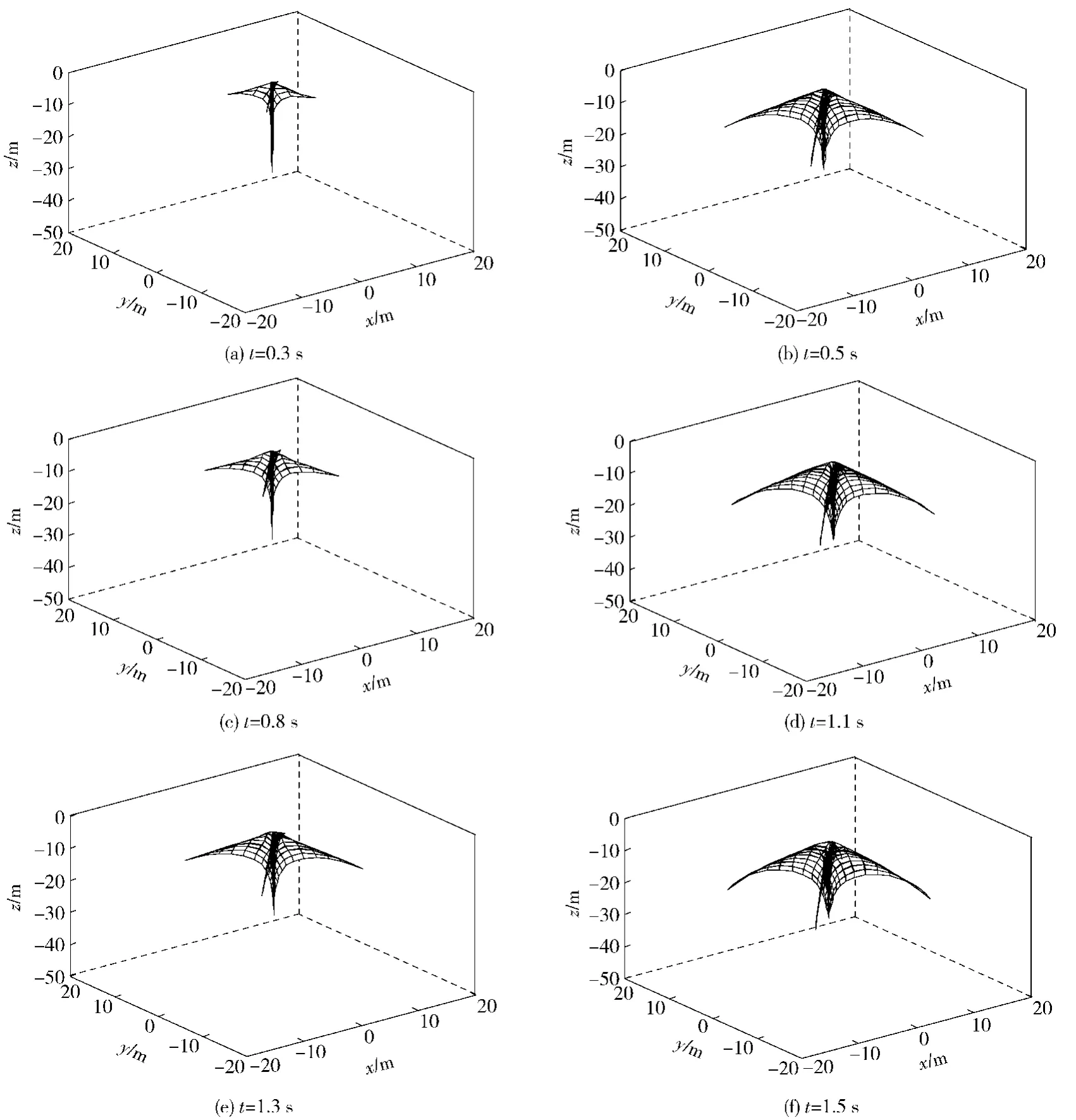
图9 空间绳网二级展开位型图Fig. 9 The shape of space nets during deployment

式中：R代表质量块位移矢径在沿飞网发射方向上的投影距离；下标代表质量块沿同一方向的顺序编号。

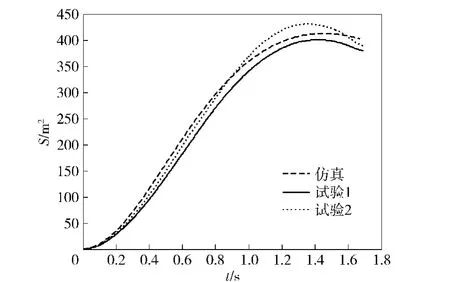
图10 绳网展开面积仿真与试验结果对比（二级发射模式）Fig. 10 Area of net during deployment（the two stage projection mode）

图10和图11分别给出了二级发射模式下绳网展开面积和飞行距离D的仿真结果与试验结果对比曲线。虽然两条试验曲线试验工况相同，但结果仍然存在一定的差值，说明绳网作为一个复杂的柔性系统具有一定的不确定性。尽管如此，仍可以看出在绳网拉出展开过程中绳网展开面积以及飞行距离的仿真结果与试验结果具有较好的一致性。另外，由于空气阻力及重力作用的影响，绳网展开面积远小于绳网设计面积也是符合实际情况的。

图11 绳网飞行距离仿真与试验结果对比（二级发射模式）Fig. 11 Flight distance of net during deployment （the two stage projection mode）

图12和图13分别给出了两种发射模式下绳网展开面积和飞行距离的仿真结果，二级发射模式下绳网的最大展开面积以及飞行距离均明显高于一级发射模式。与一级发射模式相比，二级发射模式在绳网展开性能方面具有明显的优越性。

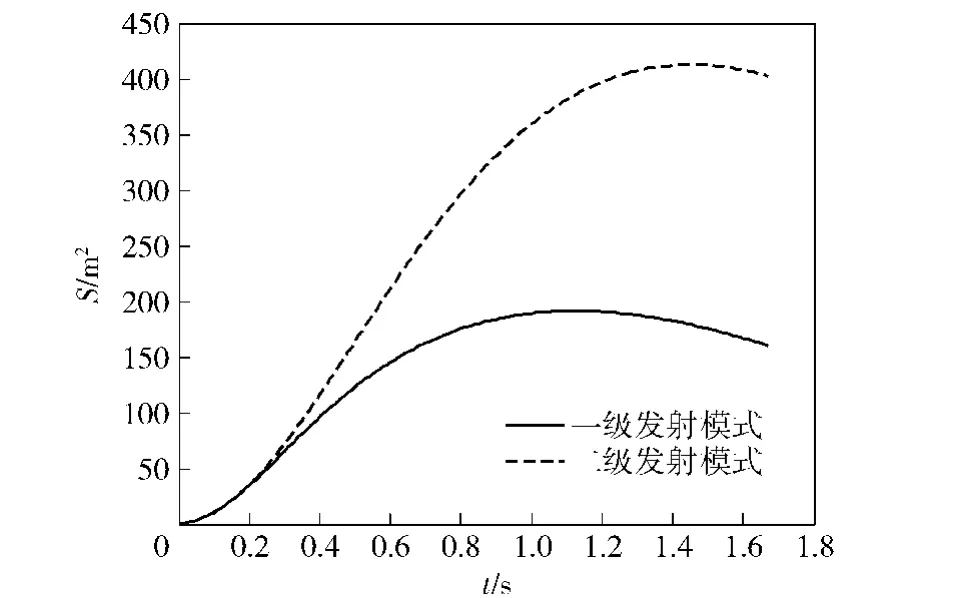
图12 不同发射模式下的绳网展开面积Fig. 12 Extended area of net in different projection modes

在上述动力学模型基础之上，继续研究了绳网在太空环境下的最大展开面积与一级发射参数之间的影响关系。在太空环境下，忽略空气阻力和重力的影响，固定二级发射速度为υs=25 m/ s，二级发射角度为α=55°，取一级发射速度υf和延时点火长度Ls分别为5 m/ s、6 m/ s、7 m/ s、8 m/ s、9 m/ s、10 m/ s、11 m/ s和2 m、7 m、12 m、17 m、22 m、27 m，得到如图14的仿真结果。

从图14可以看出：在选定参数范围内，绳网最大展开面积随一级点火长度Ls的增加先增大、后减小，随一级发射速度υf的增大而增大。在（Ls= 7 m，υf= 11 m/ s）、（Ls= 12 m，υf= 11 m/ s）以及（Ls=12 m，υf= 10 m/ s）3种工况下已经达到了甚至超过了绳网设计面积（绳网存在一定的弹性）；但在（Ls=2 m，υf=5 m/ s）工况下，绳网的最大展开面积仅约为1 460 m2.

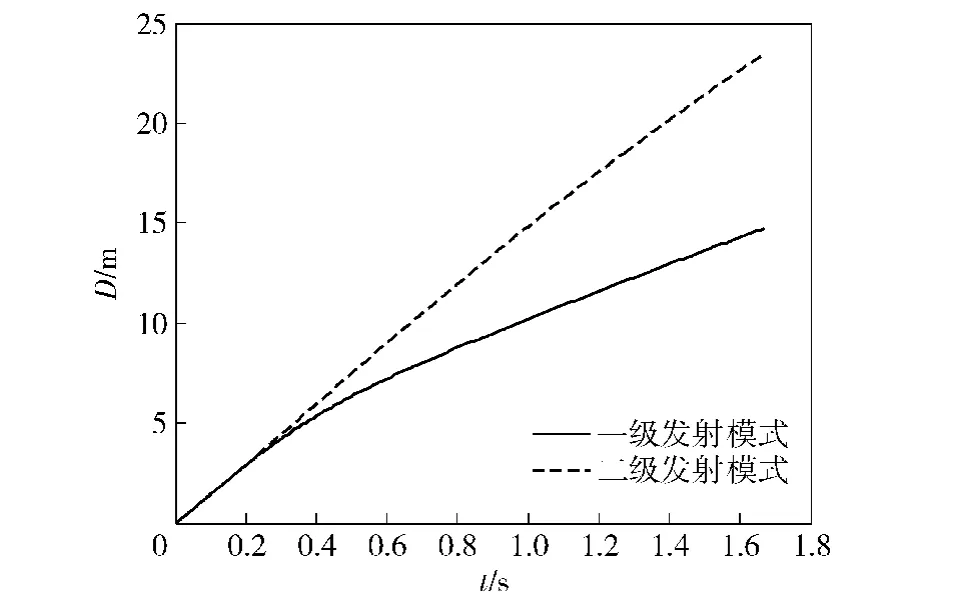
图13 不同发射模式下的绳网飞行距离Fig. 13 Flight distance of net in different projection modes

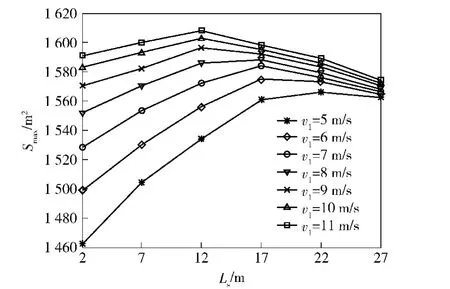
图14 绳网最大展开面积与延时点火长度关系Fig. 14 Max area vs length of projection delay

分析可知，由于消除了空气阻力和重力的影响，绳网最大展开面积远大于地面试验情况，在参数合理的情况下可以达到完全展开。

在空间绳网二级发射模式下，绳网能否更好地达到设计面积与发射参数间的匹配关系有关。绳网中心点与网舱盖（质量mf）相连，一级发射装置点火使得绳网中心点获得一定的初速度υf，二级发射装置点火使得绳网4个角点质量块（质量ms）获得初速度υs，绳网中心点和角点速度的匹配情况直接影响绳网构型变化。当二者存在差值时，动量就会通过柔性绳网进行传递，重新分配。在这个交换的过程中伴随有系统能量的衰减，以及绳网构型的变化。

仿真的结果表明：二级发射模式下，延时点火长度和一级发射速度等各项发射参数对空间绳网的展开性能影响较大，在仿真试验工况范围内，在（Ls=12 m，υf=11 m/ s）时，展开性能达到相对最优。通过加大仿真参数密度，可以获得使展开性能达到最佳的精确发射参数组合。

4 结论

空间绳网是一种具有潜在应用价值的新型空间结构。本文提出空间绳网的二级发射模式，并进行了动力学建模与分析，初步得到以下结论：

1）空间绳网二级发射模式有助于避免绳网展开过程中出现的缠绕打结问题，具有可行性，是空间绳网发射模式的一种新思路。

2）仿真结果与试验数据基本吻合，数值仿真模型有效，可以作为空间绳网发射优化设计的参考依据。

3）在给定发射参数范围内，可以使用文中所建立的仿真程序计算得到最优发射参数组合，使得绳网展开性能最佳。

参考文献（References）

［1］ 刘海涛.空间绳网展开及复合体离轨动力学与控制［D］.长沙：国防科学技术大学，2014. LIU Hai-tao. Dynamics and control of space net deployment and combination reorbiting［D］. Changsha：National University of Defense Technology，2014.（in Chinese）

［2］ Sinn T，McRobb M，Wujek A. Results of REXUS12s suaineadh experiment deployment of a spinning space web in micro gravity conditions［C］∥63rd International Astronautical. Congress. Naples，Italy：The Suaineadh Team，2012.

［3］ Mankala K K，Agrawal S K. Dynamic modeling and simulation of impact in tether net/ gripper systems［J］. Multibody System Dynamics，2004，11（3）：235 -250.

［4］ Summerer L，Purcell O，Vasile M，et al. Making the first steps towards solar power from space-microgravity experiments testing the deployment of large antennas［C］∥60th International Astronautical Congress. Daejeon，Korea：International Astronautical Federation，2009.

［5］ Gärdsback M，Tibert G. Optimal deployment control of spinning space webs and membranes［J］. Journal of Guidance，Control，and Dynamics，2009，32（5）：1519 -1530.

［6］ Gärdsback M，Tibert G. Deployment control of spinning space webs［J］. Journal of Guidance，Control，and Dynamics，2009，32（1）：40 -50.

［7］ Palmerini G B，Sgubini S，Sabatini M. Space webs based on rotating tethered formations［J］. Acta Astronautica，2009，65（1/2）：131 -145.

［8］ Sakamoto H，Natori M C，Kadonishi S，et al. Folding patterns of planar gossamer space structures consisting of membranes and booms［J］. Acta Astronautica，2014，94（1）：34 -41.

［9］ Haraguchi D，Sakamoto H，Shirasawa Y，et al. Design criteria for spin deployment of gossamer structures considering nutation dynamics［C］∥AIAA Guidance，Navigation，and Control Conference. Toronto，Canada：American Institute of Aeronautics and Astronautics，2010.

［10］ 王波，郭吉丰.采用超声波电机的空间飞网自适应收口机构设计［J］.宇航学报，2013，34（3）：308 -313. WANG Bo，GUO Ji-feng. Design of self-adaptative take-up mechanism for space net using ultrasonic motor［J］. Journal of Astronautics，2013，34（3）：308 -313.（in Chinese）

［11］ 刘海涛，张青斌，杨乐平，等.空间绳网系统展开动力学特性分析［J］.国防科技大学学报，2015，37（3）：68 -77. LIU Hai-tao，ZHANG Qing-bin，YANG Le-ping，et al. The deployment dynamic characteristics analysis of space web system ［J］. Journal of National University of Defense Technology，2015，37（3）：68 -77.（in Chinese）

［12］ 张青斌，孙国鹏，丰志伟，等.柔性绳网动力学建模与天地差异性分析［J］.宇航学报，2014，35（8）：871 -877. ZHANG Qing-bin，SUN Guo-peng，FENG Zhi-wei，et al. Dynamic modeling and difference analysis between space and ground for flexible nets［J］. Journal of Astronautics，2014，35（8）：871 -877.（in Chinese）

［13］ Zhai G，Zhang J R，Zhang Y. Circular orbit target capture using space tether-net system［J］. Mathematical Problems in Engineering，2013，2013（4）：1 -11.

［14］ 高智杰，孙富春，闵海波，等.飞网抛射过程母卫星姿态干扰分析与姿态控制［J］.力学学报，2013，45（3）：434 -441. GAO Zhi-jie，SUN Fu-chun，MIN Hai-bo，et al. Study on attitude disturbance and control of mother satellite during space net projecting［J］. Chinese Journal of Theoretical and Applied Mechanics，2013，45（3）：434 -441.（in Chinese）

［15］ 王波，郭吉丰.空间飞网质量块动力学分析及收口机构优化设计［J］.宇航学报，2012，33（10）：1377 -1383. WANG Bo，GUO Ji-feng. Dynamics analysis of mass block and optimization design of take-up mechanism for space net［J］. Journal of Astronautics，2012，33（10）：1377 -1383.（in Chinese）

［16］ 陈钦，杨乐平，张青斌.空间飞网发射动力学建模仿真研究与地面试验［J］.国防科技大学学报，2009，31（3）：16 -19. CHEN Qing，YANG Le-ping，ZHANG Qing-bin. Dynamic model and simulation of orbital net casting and ground test［J］. Journal of National University of Defense Technology，2009，31（3）：16 -19.（in Chinese）

Dynamics Analysis of a Two-stage Projection Scheme of Space Nets System

GAO Qing-yu，TANG Qian-gang，ZHANG Qing-bin，FENG Zhi-wei
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，Hunan，China）

Abstract：A two-stage projection scheme of space nets is proposed by using“outstretching first and opening later”idea in parachute inflation process，and a numerical simulation model is developed. In the proposed scheme，the projection process of space nets is divided into two successive courses：the first-stage of outstretching course and the second-stage of opening course，through which the process is controlled step by step to pull out the space nets regularly and ordinarily，and avoid their twining，penetration and knotting problems. Through a contrastive analysis of the numerical simulation result and the experiment result，the numerical simulation model is tested and verified. The two-stage projection scheme of space nets and the numerical simulation model developed in this paper provide a reference way to carry out optimization design of space nets.

Key words：aircraft launch and recovery，flight technology；space net；dynamic modeling；two-stage projection；numerical simulation；optimization design

中图分类号：V423

文献标志码：A

文章编号：1000-1093（2016）04-0719-08

DOI：10. 3969/ j. issn. 1000-1093. 2016. 04. 021

收稿日期：2015-06-16

基金项目：国家自然科学基金项目（11272345）

作者简介：唐乾刚（1958—），男，教授，博士生导师。E-mail：kdtqg@ sina. com；