磁场抑制聚能射流颗粒翻转研究

马彬，黄正祥，祖旭东，肖强强，贾鑫（南京理工大学机械工程学院，江苏南京210094）



磁场抑制聚能射流颗粒翻转研究

马彬，黄正祥，祖旭东，肖强强，贾鑫
（南京理工大学机械工程学院，江苏南京210094）

摘要：通过分析磁场与聚能射流的耦合作用过程，在断裂射流颗粒发生小角度翻转的情况下，建立了当有磁场存在时聚能射流颗粒的翻转运动方程。在此基础上，采用电磁场Ansoft Maxwell分析软件仿真的方法研究了翻转射流颗粒在磁场中所受力以及力矩特性，并对结果进行了实验验证。研究结果表明:聚能射流颗粒在强磁场中的翻转运动方程能较好地描述磁场对其翻转的抑制过程，数值模拟所得射流颗粒的受力以及力矩进一步反映磁场对翻转射流颗粒的抑制特性。实验结果验证了杵体在磁场的作用下，其翻转受到修正和抑制，最终其轴线基本与射流侵彻通道轴线一致。

关键词：兵器科学与技术；聚能射流；磁场；翻转；振荡

黄正祥（1967—），男，教授，博士生导师。E-mail：huangyu@ mail. njust. edu. cn

0 引言

炸高是影响聚能装药破甲威力的主要影响因素之一。尤其是在大炸高情况下，由于聚能射流容易发生失稳断裂，破甲威力难以提高。在破甲弹方面，国内与国外相比，主要存在的问题表现在大炸高条件下破甲威力和穿深稳定性有一定差距［1］。随着现代技术的发展，防护技术也不断提升，间隙装甲、复合装甲以及栅格装甲逐步投入战场。这些装甲的主要作用原理就是使聚能射流提早断裂，同时增加聚能装药的炸高，利用其空隙使聚能射流出现断裂失稳，从而达到减小破甲战斗部毁伤效果的目的［2］。为了有效对付这类新型装甲，就需要增加大炸高下聚能射流的稳定性，从而提高其侵彻能力。

聚能射流断裂后的翻转是影响其侵彻能力的重要因素之一。小炸高情况下，聚能射流翻转对其作用效果影响较小，但随着炸高的增加，聚能射流颗粒的翻转对侵彻能力的影响愈来愈明显。在侵彻过程中，当射流颗粒的速度降低到临界侵彻速度时，侵彻过程将会停止。在相关的研究中，通常假设这种侵彻的停止是由射流颗粒与射流通道的侧向接触导致的，引起侧向接触的原因之一就是射流的漂移和翻转［1］。本文则是通过外加磁场的方法，抑制和修正聚能射流的翻转，从而使聚能射流具有良好的一致性。

Rottenkolber等［3］通过理论模型描述了断裂聚能射流颗粒的翻转运动，并且得出引起射流翻转的主要因素不是轴向力而是侧向力，同时，通过计算以及相关的测量给出了聚能射流翻转过程中的一些相关参数。Mayseless等［4］提出了一个描述在大炸高下聚能射流漂移和翻转的新模型，模型中，假设射流散布的来源是断裂以及加工不对称，并且将理论计算的结果与实验进行了对比。Mayseless等［5］还通过计算以及实验对比，说明了射流的不对称约束以及不对称起爆对聚能射流一致性的影响。Hirsch［6］建立了用于计算断裂射流颗粒散布角的理论模型，详细论述了聚能射流颗粒的分散机制，模型中，射流颗粒翻转的频率被看作射流的颗粒速度以及最终长度的函数，通过计算同样得到当射流颗粒开始接触侵彻通道的壁面时侵彻过程结束，其理论结果得到了实验验证。

上述的许多学者对射流的翻转以及漂移进行了相关的研究。从研究成果可以得出，射流的翻转主要是由于加工精度、起爆对称性以及其他一些外界因素引起的。现阶段对于提高聚能射流的侵彻威力的研究主要集中于对新结构药型罩的设计［7-8］、药型罩新材料的应用［9］、炸药性能的提高、起爆方式的选择以及加工工艺的改进［10］等方面，但是现阶段所采用的手段对聚能装药侵彻效能的提高是有限的，并且存在很大的局限性。因此，在磁荷理论的基础上，对外加磁场抑制聚能射流的翻转机制进行研究有广阔的应用前景。外加磁场抑制聚能射流颗粒翻转技术目前是提升常规聚能射流毁伤效能的新概念技术之一，其突破了传统依靠提高机械加工精度增加聚能射流稳定性的模式，利用电磁感应过程中形成的电磁力，对偏离轴线的聚能射流颗粒进行修正，从而使偏离轴线的射流颗粒重新回到轴线方向，增加了聚能射流的一致性，对增加聚能装药的侵彻威力有重要意义。

1 理论模型

先前的许多实验研究结果表明［3 -4，11］，聚能射流在自然状态下发生断裂，其断裂后并不是沿轴线一致排列，而会发生一定的翻转和漂移，如图1所示。

图1 聚能射流自然情况下断裂的X光照片［3］Fig. 1 X-ray radiograph of the naturally broken shaped charge jet

通过图1所给的X光照片可以看到，自然情况下，一些断裂的射流微元飞行方向已经与射流的轴线方向形成了一定的夹角，并且，由于所受空气阻力的不对称，将导致射流颗粒更严重的偏离轴线。这些发生翻转的射流颗粒在侵彻过程中其有效长度将减小，由于射流的侵彻能力正比于其有效长度［12］，因此，射流的侵彻能力随之降低。本研究在等效磁荷理论［13］的基础上建立了聚能射流颗粒的受力模型，通过理论分析，得到了聚能射流在磁场中的翻转运动方程。聚能射流与外加磁场的耦合作用示意图如图2所示。

1. 1 磁场作用对翻转射流微元产生力矩作用

为了简化问题，假设断裂并且发生翻转的聚能射流颗粒为圆柱体，并对其进行受力分析。通过分析可知，当射流在外加磁场中发生断裂且翻转时，其主要受到空气阻力、自身重力以及磁场力的作用，并且假设聚能射流的翻转运动是中心对称的，其对称中心是其重心，其受力示意图如图3所示。由于射流颗粒的翻转是中心对称的，因此本研究中选择射流颗粒的一个端面（端面1）进行受力研究。

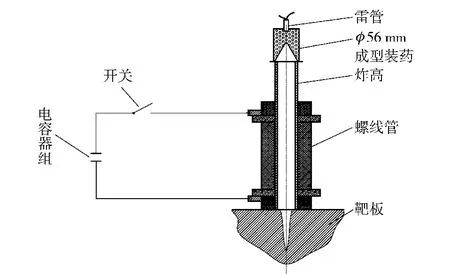
图2 聚能射流与强磁场耦合示意图Fig. 2 Interaction of jet and magnetic field

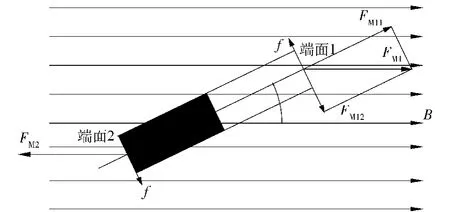
图3 在磁场中偏离轴线的射流颗粒受力示意图Fig. 3 The force diagram of the shaped charge jet particles deviating from the axis in magnetic field

基于磁荷理论，磁体内部的最小单元是磁偶极子，在导体未被磁化时，各个磁偶极子的趋向是杂乱无章的，它们之间的磁偶极矩相互抵消，导体不呈现磁性。当导体受到外界磁场作用时，其内部的磁偶极子将按照一定的方向整齐的排列，首尾相接，因此在导体的两端将会表现出磁性。在研究过程中，由于“磁场冻结”效应［14］，射流断裂后，其内部磁场方向仍平行于轴线方向，受磁场作用的射流颗粒内部磁偶极子整齐地排列，并且首尾衔接，相互抵消，其宏观效果就是整个射流颗粒的两个端面上分布有正负磁荷。

磁偶极子在均匀外加磁场中所受力矩公式［13］为

式中：P =φl为磁偶极矩，φ为磁荷量，l为从负磁荷到正磁荷的位移矢量；H表示外加磁场的磁场强度。

为了求解磁荷量，这里引入磁荷密度ρm，即单位面积上的磁荷，它与磁场强度的关系为

因此，在射流颗粒截面上，正负磁荷量值均为

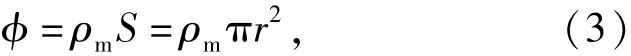
式中：r为射流颗粒的半径。它与初始半径R0的关系［15］为，其中，为聚能射流的初始应变率。将其代入（3）式可得

研究中，从负磁荷到正磁荷的位移矢量数值就是射流颗粒的长度lj，其与该射流颗粒初始长度l0的关系为lj= l0（1 +t）.结合（4）式，可得磁偶极矩为

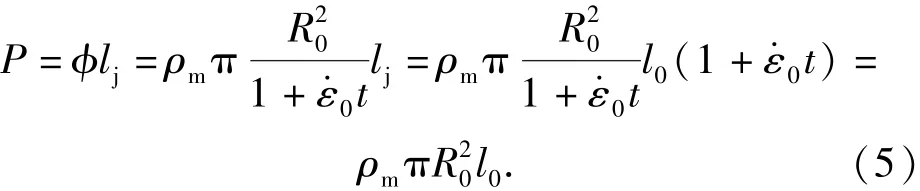
将（5）式代入（1）式，可得到射流在磁场作用下电磁力对射流颗粒产生的转动力矩：

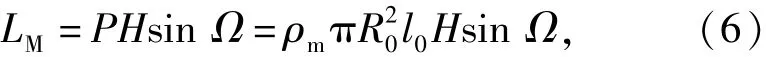
式中：Ω表示断裂聚能射流颗粒轴线与磁感线方向的之间的夹角。

在受磁场作用的介质中，磁场强度与磁感应强度的关系［13］为

式中：ψ表示磁化强度。

将（7）式代入（6）式，可以得到射流在磁场作用下电磁力对射流颗粒产生的转动力矩表达式为

1. 2 重力以及空气阻力对断裂射流微元翻转力矩的影响

由于射流微元还受到重力以及空气阻力的影响，下面将对这两种力产生的转矩进行分析。因为只有垂直于射流轴线方向的分力才会对射流的翻转产生影响，因此在分析过程中只考虑垂直于射流轴线方向的分力。

端面1：

端面2：

经过分析，端面2和端面1所受的重力以及空气阻力大小是完全相同的，因此可以得到

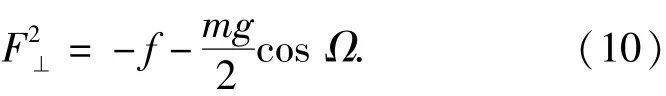
端面1和端面2处的受力相对于聚能射流微元中心的力矩分别为

因此，根据上述分析，就可得到在外加磁场中断裂并翻转的聚能射流颗粒所受总力矩为

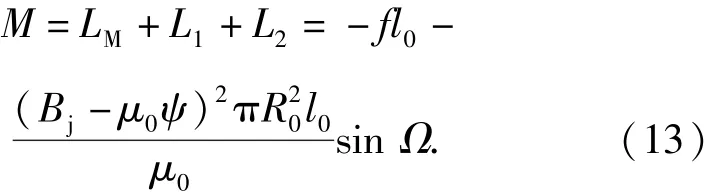
1. 3 翻转射流在磁场中的翻转运动方程

根据上面的分析，若能得到射流颗粒磁化强度以及偏离轴线的角度，就可以得到各个时刻射流所受磁场作用的力矩。此力矩将抑制射流偏离其轴线，使受磁场作用的射流颗粒保持在同一轴线上，在其他条件相同情况下，能够增加聚能射流作用效果。

根据刚体定轴转动的转动定律，可以得到射流颗粒旋转时转矩的另一表达式［16］为

结合上面两个表达式，可以得到

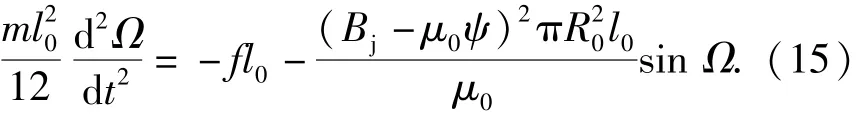
进一步整理得到

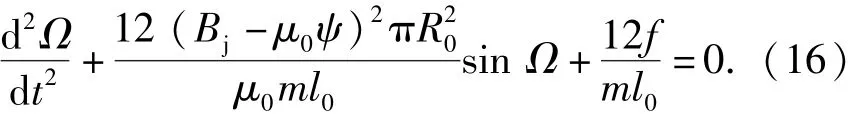
为了求解射流颗粒的翻转运动方程，研究中假设射流颗粒在翻转过程中受到的空气阻力与其翻转速度呈正比。假设其比例关系满足（17）式［17］：

式中：β为阻尼因子；υ为翻转时的切线速度。

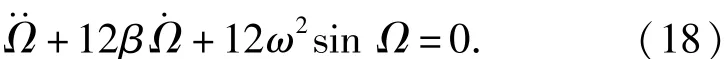
假设射流微元轴线与药型罩轴线的夹角为较小值，因此sin Ω≈Ω，上述方程可以简化为+12β+ 12ω2Ω=0，此时方程的解为

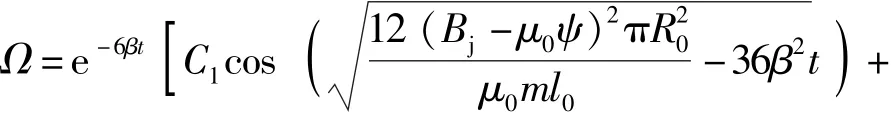
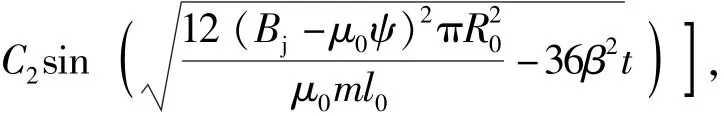
式中：C1和C2都是由初始条件决定的。

2 数值模拟

为了研究磁场对翻转射流颗粒的抑制作用机理，本文使用电磁场Ansoft Maxwell数值模拟软件进行仿真研究。

仿真时的磁体模型按照实验所用实物参数进行建模。实验所用磁体参数以及其他相关参数如表1所示。仿真中对聚能射流颗粒进行了简化，将其看作为等截面的圆柱体。模型参数：半径为3. 2 mm，长度为20 mm，材料为紫铜。所建模型如图4所示（为了展现射流颗粒，此处给出了磁体的二分之一模型，实际仿真是全模型建模）。聚能射流颗粒中心通过磁体轴线，且颗粒轴线与磁体轴线之间的夹角设定为10°.

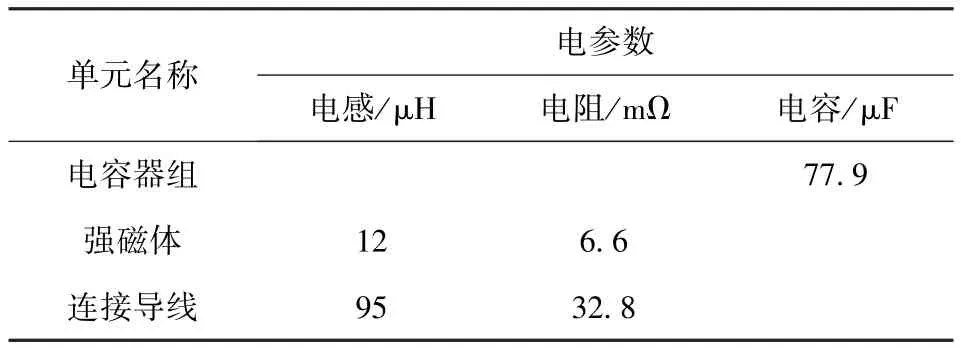
表1 测量参数Tab. 1 Measured parameters

图4 仿真模型示意图Fig. 4 Simulation model

外电路主要由电容器组、传输导线以及负载三部分组成。电容器组为4台并联，强磁体使用矩形截面铜导线按照双层结构并联，连接导线使用截面为41. 5 mm2的铜排。电容器组、强磁体以及导线的相关电参数是经测量在外电路设置中直接设置，相关参数如表1所示。

仿真中按照实际电参数进行外电路设置，得到与实际电路相吻合的激励电路。经过理论计算、仿真以及实验，得到了放电电流的理论计算结果、仿真结果以及实验结果，如图5所示。

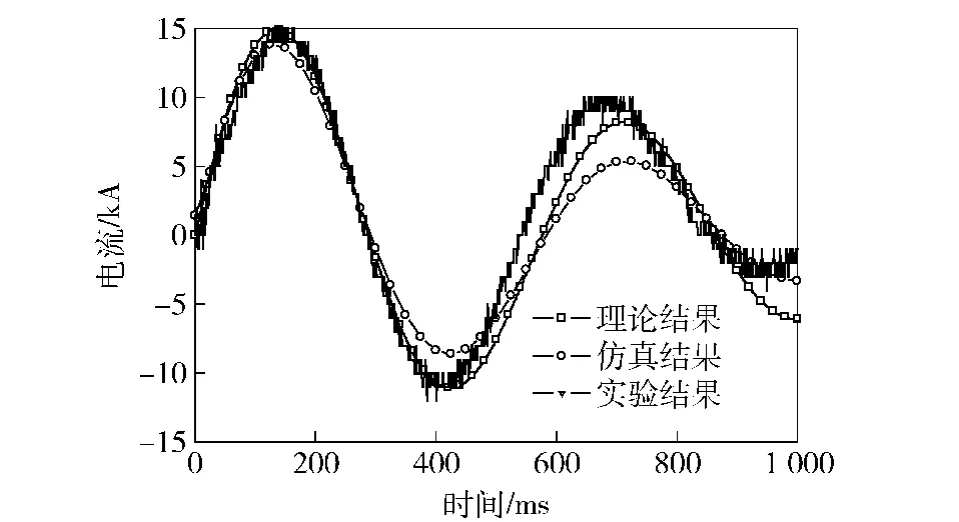
图5 动态放电电流随时间变化曲线Fig. 5 Dynamic discharge current vs. time

通过图5，对比理论计算结果、仿真结果与实验所测信号可得，在前400 μs三者十分吻合，然而，随着时间的推移，三者之间逐渐出现了一定的误差。误差产生的原因如下：1）本文理论计算仅考虑强电流工作而产生的热量用于升高导体的温度，而忽略了热量向周围环境的散失；2）温度的增加对电感也将产生一定程度的影响，温度对电感的影响相比对电阻率的影响小，因此本文未考虑温度对电感的影响；3）仿真中外加电路的设置虽按实际参数进行了相关设置，但是仿真中的一些外部环境是理想的，因此，仍与实际情况有一定区别；4）电路信号的测量是根据电磁感应原理进行的，因此，设备的测量精度以及自然环境中的磁场影响也是引起误差不可避免的因素。通过图5可以看出，在1 000 μs内三者之间的误差相对较小，能够满足精度要求。

通过仿真，得到了125 μs时磁感应强度的矢量以及聚能射流颗粒上的磁感应强度分布，如图6所示。

从图6（a）中可以看出，磁感应强度在靠近磁体轴线的位置处分布较为均匀，且磁感应强度矢量平行于轴线。根据图6（b）的仿真结果可得，在125 μs时，聚能射流颗粒模型内磁感应强度近似3 T，由于射流颗粒轴线与z轴存在一定夹角，使得沿z方向不再对称，由此造成磁感应强度的分布不均匀。同时，由于磁感应强度的不均匀分布导致最终的电磁力对聚能射流颗粒进行修正，使射流颗粒轴线与磁体轴线重合。

通过仿真，得到聚能射流颗粒所受分力的各分量以及磁力随时间的变化曲线，如图7所示。从图7可以看出，各分力以及磁力之间随时间周期性变化，并且磁力的幅值相对较大。为了判断磁力的产生是否对偏转射流颗粒起到修正作用，下面对射流颗粒在有外加磁场情况下的力矩进行分析。

图6 t =125 μs时磁感应强度的矢量图以及聚能射流颗粒上的磁感应强度分布图Fig. 6 The vector diagram of magnetic induction and the distribution of magnetic induction intensity inside the shaped charge jet particle at 125 μs

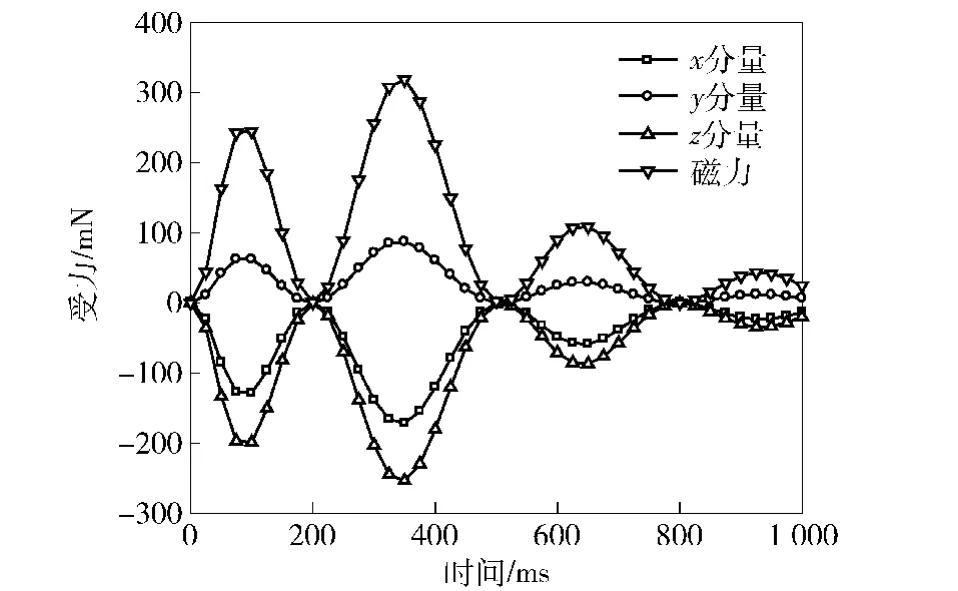
图7 射流颗粒沿不同轴线的受力以及磁场力随时间的变化Fig. 7 Evolution of force and magnetic force inside the jet particle

图8为聚能射流颗粒模型的相对于各轴线的力矩分量随时间的变化曲线。由图8可知，相对于x轴的力矩起主导作用，相对于x轴的力矩在极短时间段内呈现负值，这是由于磁体中电流反向，射流颗粒内部的类磁滞效应所致，由于时间极短，并不会对整体作用效果造成影响。根据右手定则可知，相对x轴的力矩作用效果是迫使聚能射流颗粒沿其中心逆时针转动，即在外加磁场的作用下，使其轴线逐渐与强磁体的轴线相重合，最终对发生偏转的聚能射流颗粒进行了抑制和修正。而其他两个力矩分量与相对于x轴的分量比较小，其作用效果几乎可忽略不计。

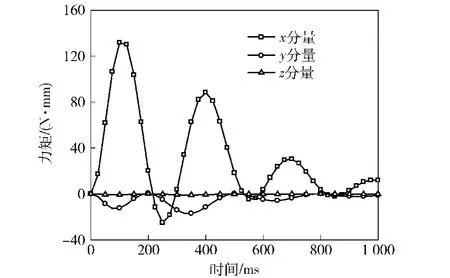
图8 扭矩分量随时间的变化Fig. 8 Torque component vs. time

3 实验研究

图9所示为电路结构示意图。实验过程中，根据图9所示即可进行实验电路连接。

整个实验过程中，使用电容器供电。当电容器两端的电压达到实验设定值时，通过爆炸开关驱动闭合回路，使实验电路瞬间闭合。电路为强磁体提供电流，从而产生纵向磁场，用于抑制和修正聚能射流颗粒翻转。实验布置如图10所示。

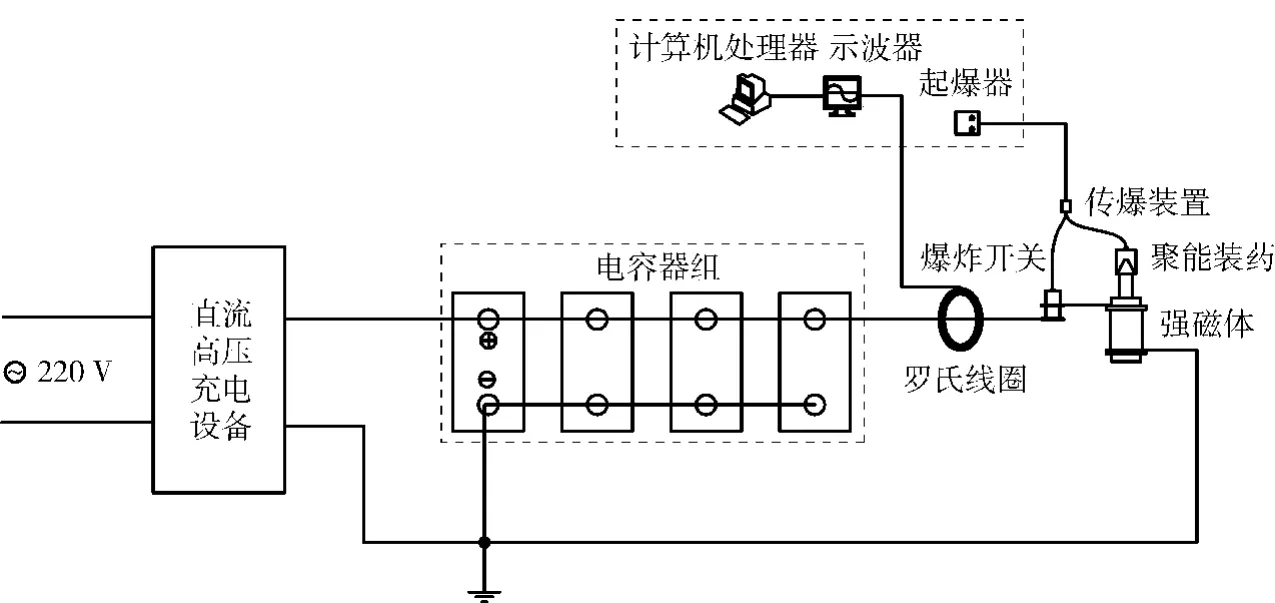
图9 电路结构示意图Fig. 9 Structural diagram of experimental circuit

图10 实验装置图Fig. 10 The experimental arrangement

4 结果与讨论

4. 1 理论结果分析

理论计算过程中，假设聚能射流颗粒的初始翻转角度为10°，并且起始时刻的翻转角速度为0，因此可以得到如下的初始条件：

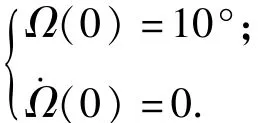
根据上述推导所得聚能射流颗粒翻转运动的运动方程以及所给的初始条件，通过理论计算获得了不同磁感应强度下聚能射流颗粒翻转角度随时间的变化情况，如图11所示。图11中分别给出了外加磁场的磁感应强度为2 T、4 T、6 T、8 T、10 T时的变化情况。

研究过程中，着重从理论上研究了断裂并且翻转的聚能射流颗粒通过预先产生的磁场时磁场对射流颗粒翻转的抑制以及修正。从上述计算结果可以看出，在不同磁感应强度下，聚能射流颗粒的翻转角度随着时间推移，其振动幅值越来越小。计算结果充分表明，磁场的作用抑制了聚能射流颗粒的翻转，逐渐使发生翻转的聚能射流颗粒回到轴线方向。

4. 2 实验结果分析

所得实验结果如图12和图13所示。图12表示的是侵彻靶板的表面，图13为剖分后的侵彻靶板照片。实验过程中，设定的炸高分别为490 mm和650 mm.其中，A、B、D 3组实验的炸高设定为490 mm，其余3组实验炸高为650 mm；A、B、C 3组实验未加外磁场干扰，D、E、F实验存在外加磁场。为了验证理论模型的正确性，分析过程中选择易于观察和分析的杵体为验证对象，与理论结果进行对比。

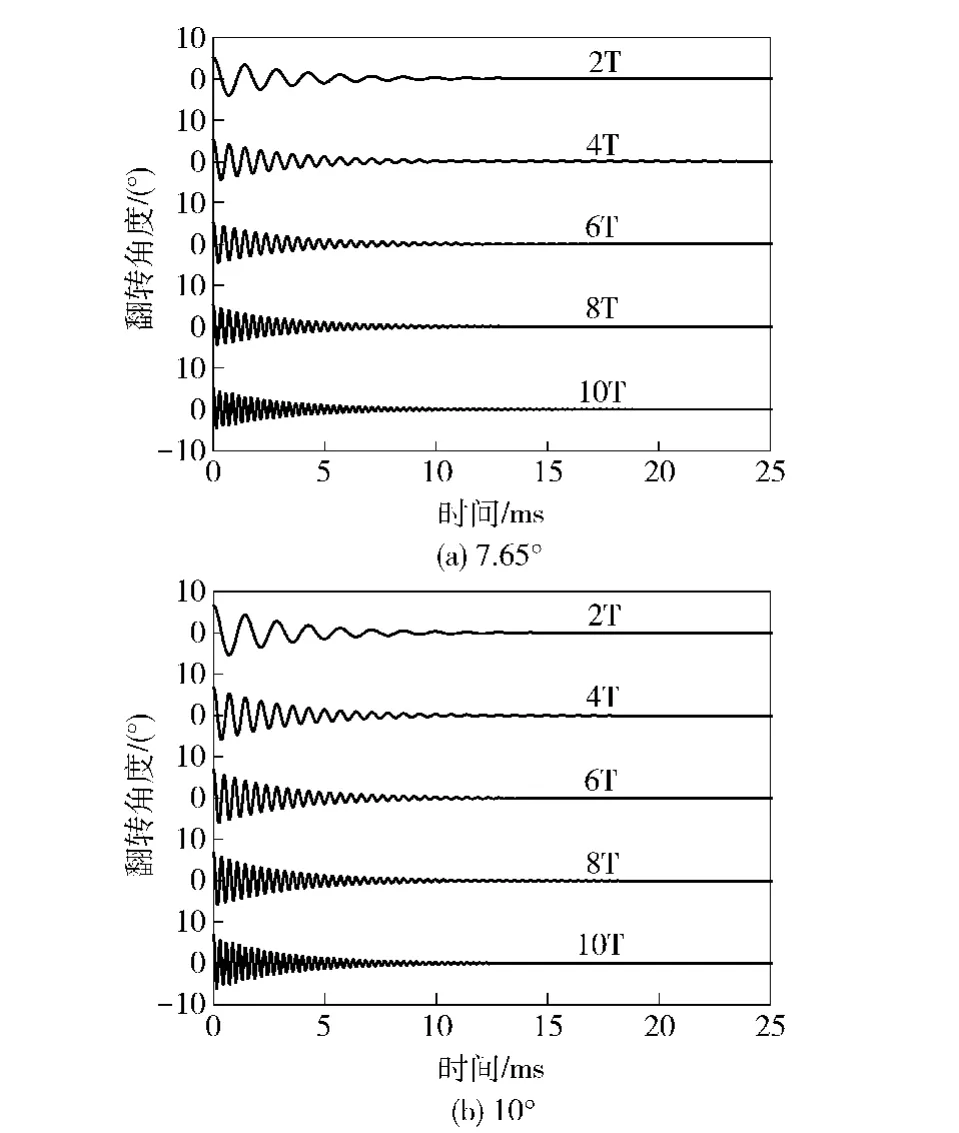
图11 初始翻转角度为7. 65°和10°的断裂射流颗粒通过不同强度磁场时其翻转角度随时间的变化Fig.11 The changes of turning angle of jet particles passing through magnetic fields with the different intensities over time

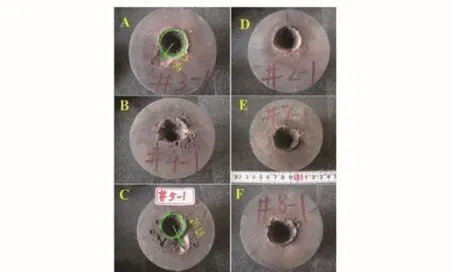
图12 不同情况下侵彻靶板表面照片Fig. 12 The surfaces of the experimental targets under different conditions

图13 实验靶板剖面图Fig. 13 Experimental results of split targets penetrated by shaped charge jet

从图12可以看出，在未施加磁场的3组实验中，侵彻靶板表面都有明显的杵体偏移而造成的侵彻坑洞。这说明：在未施加磁场干扰时，杵体发生了翻转偏移，而没有与聚能射流保持同轴。由D、E、F 3组存在磁场作用的实验结果可以看出，其表面未发现杵体冲击而造成的坑洞。初步说明，磁场的加载对杵体的运动状态有一定的影响。为了进一步确定杵体的状态，对侵彻靶板进行了剖分观察，其结果如图13所示。

根据图13的靶板剖分结果可知，未施加磁场的3组实验的A和C实验中，靶板侵彻通道中未发现杵体，与图12中结果相对应，说明杵体偏离了射流运动的轴线，未进入射流侵彻通道，而与靶板表面发生碰撞，形成一定深度的坑洞。B实验中，杵体部分进入了射流侵彻通道，但通过观察可以发现，杵体（图13中B-1-1和B-1-2）的轴线与射流通道的轴线呈一定的夹角。根据测量可知，杵体B-1-1部分最终与射流侵彻通道轴线的夹角为13°，B-1-2部分与其夹角增大至23°.这充分说明，杵体在运动过程中已经发生了翻转，并且随着运动距离的增加，偏转角度不断增加。同时，翻转近似呈现中心对称，与理论模型的假设相符，进一步验证了理论假设的正确性。另外，通过施加磁场的D、E、F 3组实验的靶板剖分图可以看出，3组实验中，杵体全进入射流通道，并且杵体（图13中D-1-1、E-1-1、F-1-1以及F-1-2）的轴线基本都与聚能射流的侵彻通道轴线保持一致。经过6组实验结果的分析和对比，说明外加磁场对杵体的翻转起到了抑制和修正的作用，与理论模型得到的结论相一致，验证了理论模型的正确性。

本文以A和C两组实验（以下简称实验A和实验C）为例，进行相关定量分析。首先给出如下假设：1）杵体在即将进入强磁体时，由于不平衡外力或扰动而发生翻转；2）杵体始终沿其轴线方向运动。

偏转角度的计算示意图如图14所示，其中，Δd表示强磁体入口到靶板表面之间的距离，Δs表示在靶板表面杵体中心偏离聚能射流通道轴线的距离。根据以上两个参数可得杵体进入强磁体时其偏转初始角度为

图14 偏转角度计算示意图Fig. 14 The calculating diagram of deflecting angle

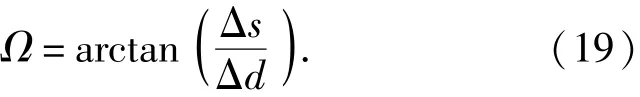
在A和C两组实验中，强磁体的入口距靶板表面的距离均为Δd = 195 mm.根据测量结果（见图8），可得实验A中在靶板表面杵体中心偏离聚能射流通道轴线的距离Δs =34. 73 mm，实验C中偏移距离Δs =26. 18 mm.根据实验参数以及（19）式可以得到：实验A杵体进入强磁体时，其初始偏转角度为Ω（0）= 10. 49°；实验C对应的初始偏转角度为Ω（0）=7. 65°.

根据理论模型计算了初始偏转角度为7. 65°和10°情况下偏转角度分别减小到5°、3°和0. 1°时所需要的时间，如图15所示。由图15可以看出，当翻转角度减小到某一确定值时，不同磁感应强度的磁场下所需的时间基本相同。这是由于聚能射流断裂后，其颗粒相对较小，本身的重力以及所受到的空气阻力也是相对微小的，对翻转抑制以及修正的影响几乎可以忽略不计，因此，起主导作用的主要是外加磁场引起的电磁力。通过所得运动方程的解可以看到，磁感应强度改变的主要是振荡频率。同时，由图15还可得，在一定范围内，起始偏转角度越小，修正到同一偏转角度所需的时间越短。

5 结论

实验研究过程中，虽然聚能射流的侵彻威力未得到明显的提高，但通过对理论、仿真以及实验结果的分析，仍可得出如下结论：

1）假设杵体为圆柱体，建立了聚能射流颗粒在强磁场中的翻转运动方程。通过理论计算可知，在一定磁感应强度范围内，修正翻转射流颗粒所需的时间基本保持不变。

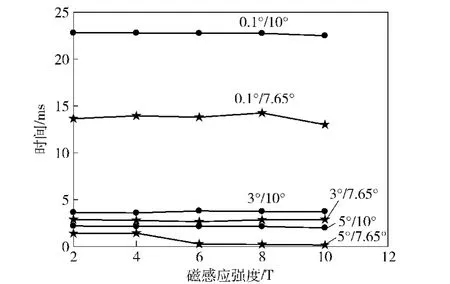
图15 不同磁感应强度下的聚能射流翻转角度变化所需的时间Fig.15 Time taken for the change of the shaped jet flip angle under different magnetic induction intensity

2）数值模拟结果表明，聚能射流颗粒在磁场中受到的力以及力矩的作用抑制了射流颗粒的翻转。

3）通过对比实验结果，杵体在运动过程中发生翻转，磁场的加入对其翻转进行了修正和抑制，最终其轴线基本与射流侵彻通道轴线一致。

4）系统时序是本研究的关键影响因素，为获得磁场与聚能射流耦合的理想效果，需要进行合理的时序设计。

参考文献（References）

［1］ 黄正祥，陈惠武，官程.大炸高条件下药型罩结构设计［J］.弹箭与制导学报，2000，20（3）：51 -53. HUANG Zheng-xiang，CHEN Hui-wu，GUAN Cheng. The design of liner under large standoff distance condition［J］. Journal of Projectiles，Rockets，Missiles and Guidance，2000，20（3）：51 -53. （in Chinese）

［2］ 朱绪强，成一，李德才，等.大炸高下破甲弹的侵彻性能研究［J］.爆破器材，2013，42（1）：47 -50. ZHU Xu-qiang，CHENG Yi，LI De-cai，et al. Penetration ofshaped charge jets under large standoff distance［J］. Explosive Materials，2013，42（1）：47 -50.（in Chinese）

［3］ Rottenkolber E，Arnold W. Rotation rates and lateral velocities of shaped charge jet particles caused by breakup［C］∥Proceedings of the 21st International Symposium on Ballistics. Adelaide，Australia：Australian Government Department of Defence，2004：845 -852.

［4］ Mayseless M，Kaufmann H，Misiuk L，et al. Very long standoff penetration of shaped-charge jets［C］∥Proceedings of the 28th International Symposium on Ballistics. Atlanta，Georgia，US：National Defense Industrial Association，2014：195 -206.

［5］ Mayseless M. Experimental and computational comparison between the effects of asymmetries on peripherally initiated and point initia-ted shaped charge［C］∥Proceedings of the 10th International Symposium on Ballistics. San Diego，US：1987：74 -83.

［6］ Hirsch E. The natural spread and tumbling of the shaped charge jet segments［J］. Propellants，Explosives，Pyrotechnics，1981，6（4）：104 -111.

［7］ 陈闯，王晓鸣，李文彬，等.双锥罩射流侵彻钢靶侵深计算模型［J］.兵工学报，2014，35（5）：604 -612. CHEN Chuan，WANG Xiao-ming，LI Wen-bin，et al. Penetration depth calculation model for biconical liner jet penetrating into steel target［J］. Acta Armamentarii，2014，35（5）：604 - 612.（in Chinese）

［8］ 郭俊，张晓伟，张庆明.大口径开孔聚能装药结构的设计方法研究［J］.兵工学报，2014，35（2）：40 -45. GUO Jun，ZHAO Xiao-wei，ZHANG Qing-ming. Design method for the shaped charge structures with large-radius perforation［J］. Acta Armamentarii，2014，35（2）：40 -45.（in Chinese）

［9］ 鄂智佳，段卓平，张晓伟，等.高密度钛合金聚能药型罩研究［J］.兵工学报，2014，35（2）：22 -26. E Zhi-jia，DUAN Zhuo-ping，ZHAO Xiao-wei，et al. Research on high-density titanium alloy shaped charge liner［J］. Acta Armamentarii，2014，35（2）：22 -26.（in Chinese）

［10］ 王成，王万军，宁建国.聚能装药对混凝土靶板的侵彻研究［J］.力学学报，2015，35（2）：22 -26. WANG Cheng，WANG Wan-jun，NING Jian-guo. Investigation on shaped charge penetration into concrete targets［J］. Chinese Journal of Theoretical and Applied Mechanics，2015，35（2）：22 -26.（in Chinese）

［11］ Schwartz A J，Kumar M，Lassila D H. Analysis of intergranular impurity concentration and the effects on the ductility of coppershaped charge jets［J］. Metallurgical and Materials Transactions A，2004，35（9）：2567 -2573.

［12］ Littlefield D L. Enhancement of stability in uniformly elongating plastic jets with electromagnetic fields［J］. Physics of Fluids A：Fluid Dynamics（1989—1993），1991，3（12）：2927 -2935.

［13］ 赵凯华，陈熙谋.电磁学［M］.第3版.北京：高等教育出版社；2011：389 -392. ZHAO Kai-hua，CHEN Xi-mou. Electromagnetism［M］. 3rd ed. Beijing：Higher Education Press，2011：389 -392.（in Chinese）

［14］ Fedorov S. Magnetic-field amplification in metal shaped-charge jets during their inertial elongation［J］. Combustion，Explosion and Shock Waves，2005，41（1）：106 -113.

［15］ Babkin A V，Ladov S V，Marinin V M，et al. Characteristics of inertially stretching shaped-charge jets in free flight［J］. Journal of Applied Mechanics and Technical Physics，1997，38（2）：171 -176.

［16］ 孙克恕.关于刚体定轴转动定律与角动量［J］.安庆师范学院学报：自然科学版，1995，1（2）：98 -98 SUN Ke-shu. About the law of rigid body fixed axis rotation and angular momentum［J］. Journal of Anqing Teachers College：Natural Sciences，1995，1（2）：98 -98.（in Chinese）

［17］ 刘国跃，龚劲涛，吴英.单摆运动的非谐振和弱阻尼修正［J］.绵阳师范学院学报，2007，26（2）：38 -41. LIU Guo-yue，GONG Jin-tao，WU Ying. An inhamonic and weak damped amendment to simple pendulum movement［J］. Journal of Mianyang Normal University，2007，26（2）：38 -41. （in Chinese）

Research on Magnetic Field Inhibiting the Rotation of Shaped Charge Jet Particles

MA Bin，HUANG Zheng-xiang，ZU Xu-dong，XIAO Qiang-qiang，JIA Xin
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

Abstract：The coupling process of magnetic field and shaped charge jet is analyzed，and an equation of rotation motion of the shaped charge jet particles in the presence of magnetic field is established in the case of small angle rotation. On this basis，a simulation method is used to study the characteristics of force and torque of jet particles in magnetic field by the software Ansoft Maxwell，and the experimental verification is also carried out. The research result show that the equation of rotation motion of the shaped charge jet particles in magnetic field could well describe the process of magnetic field inhibiting their rotation，and the numerical simulation of the force and torque of particles in magnetic field also reflects the property of inhibition. The experimental results indicate that the rotation of slug is inhibited and modified under the action of magnetic field，and the axis of slug can remain aligned with the axis of crater penetrated by the jet under the action of magnetic field.

Key words：ordnance science and technology；shaped charge jet；magnetic field；rotation；oscillation

中图分类号：TJ413.+2

文献标志码：A

文章编号：1000-1093（2016）04-0603-09

DOI：10. 3969/ j. issn. 1000-1093. 2016. 04. 005

收稿日期：2015-08-05

基金项目：国家自然科学金项目（11272157）；高等学校博士学科点专项科研基金项目（20123219120052）

作者简介：马彬（1988—），男，博士研究生。E-mail：dashu.000@163. com；