数学思想的践与行

广东省梅州市大埔县家炳第一中学高中部 廖妮娜

数学思想，是指人们对数学理论与内容的本质认识，它直接支配着数学的实践活动。所谓数学方法，是指某一数学活动过程的途径、程序、手段，它具有过程性、层次性和可操作性等特点。数学思想方法是数学的灵魂和精髓，如何在中学数学教材中体现数学思想方法，有意识地向学生渗透数学思想方法是一个十分重要的问题。数学知识的学习过程，就是学生数学基础知识与数学思想逐渐形成的过程。下面结合本人教学实践浅谈如何将数学思想方法的教育渗透到教学中。

一、数形结合思想

数形结合思想在高考中占有非常重要的地位，其“数”与“形”结合，相互渗透，把代数式的精确刻划与几何图形的直观描述相结合，使代数问题、几何问题相互转化，使抽象思维和形象思维有机结合。 更有利于学生的理解记忆。在讲授三角函数的性质时常渗透数形结合思想。

函数的性质的研究常常以图象的直观为基础，通过观察图象获得对函数性质的直观认识，然后再从代数的角度对性质作出严格表述。

图1

如在研究正弦函数的周期性时，先从正弦函数图象（图1）观察其变化规律，从数、形两个方面指出图象是如何体现这种“周而复始”的变化规律的。最后思考sin(x+2k)=sinx的公式又是如何反映函数值的“周而复始”的变化，通过对图象的特点，函数解析式的特点的描述，使学生更深刻地认识和理解正弦函数的周期性。由于三角函数是刻画周期变化现象的数学模型，对于周期函数了，我们只要认识理解它在一个周期区间上的性质就可把握整个定义域内的性质。通过图象（图2）可以更直观的归纳出正弦函数的定义域、值域、周期性、奇偶性、单调性等性质，

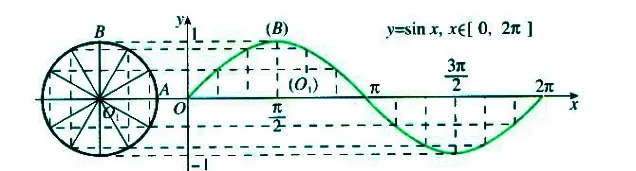
图4

学习余弦函数图象和性质时，利用诱导公式六，通过图象变换得出余弦曲线。这种变换作图，既体现了正弦函数与余弦函数的联系，又渗透了数形结合的思想。在学习正切函数图象和性质时，我们还可采用解析式y=tanx的定义域、诱导公式、正切线等研究正切函数的性质（数）。再根据性质研究正切函数的图象（形）。让学生从多个角度去思考、分析问题。在性质指导下更有效地作图、研究图象，使数形结合的思想体现得更加全面。

二、分类讨论思想

分类讨论思想就是根据所研究对象的性质差异，分各种不同的情况予以分析解决。分类讨论题覆盖知识点较多，利于考查学生的知识面、分类思想和技巧；同时方式多样，具有较高的逻辑性及很强的综 合性，树立分类讨论思想，应注重理解和掌握分类的原则、方法与技巧、做到“确定对象的全体，明确分类的 标准，分层别类不重复、不遗漏的分析讨论”。近年来，数列在大题考察中越来越注重各种数学思想的渗透，故此，探究分类讨论思想解决数列问题，对提高学生思维能力，解决数列问题有很大的作用。

三、函数与方程思想

函数与方程思想是最重要的一种数学思想，高考中所占比重大，综合知识多、题型多、应用技巧多。函数思想简单，即将所研究的问题借助建立函数关系式亦或构造中间函数，结合初等函数的图象与性质，加以分析、转化、解决有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题；方程思想即将问题中的数量关系运用数学语言转化为方程模型加以解决。

四、转化与化归思想

化归与转化的思想，就是在研究和解决数学问题时采用某种方式，借助某种函数性质、图象、公式或已知条件将，问题通过变换加以转化，进而达到解决问题的思想。应用转化与化归思想解题的原则应是化难为易、化生为熟、化繁为简，尽量是等价转化。

例：设△ABC的内角A，B，C所对的边长分别为a，b，c，且则角A的大小为________．

析：欲求角A需得关于A的三角函数方程 → (推理)根据正弦定理化已知式为角的三角函数式 → (结论)变换后得A的三角函数方程解之．

数学思想方法贯穿在整个中学数学教材的知识点中，以内隐的方式溶于数学知识的体系中，作为教师，我们首先弄清楚教材中所反映的数学思想方法以及它与数学相关知识之间的联系，并适时作出归纳和概括，在具体的授课活动中，以适当的方式将数学思想方法加以揭示，并使之表层化，使学生达到真正意义上的领会和掌握，增强学生对数学思想方法的应用意识。