浅谈高中数学教学中数形结合思想方法的渗透与学生能力的培养
云南省宣威市第七中学校 王开良
“数”与“形”是数学的基本研究对象,它们之间存在着对立统一的辩证关系。数形结合思想方法,就是在解决代数问题时,揭示出隐含在它内部的几何背景,启发思维,找到解题途径。那么在高中数学教学中如何渗透数形结合思想方法,如何培养学生运用数形结合思想解题的能力呢?
一、重视“形”的渗透,引导学生成“图”在胸
数形结合的思想方法在高中数学中应用广泛,贯穿始终。学生要能熟练的掌握和运用,并上升为学生的数学能力。首先我们得帮助学生“装”图,并成图在胸。学生胸无点墨便作不出好文章,同样在数学学习中,若学生胸中无图,又怎能数形结合!更谈不上提升数学能力。所以我们教师在教学中要潜移默化地渗透数形结合思想方法,让学生心中充满“形”,才能作出大文章。
二、重视 “形”的运用,培养学生数形结合意识
数形结合不应仅仅作为一种解题方法,而应作为一种基本的、重要的数学思想来学习、研究和掌握运用,让它真正成为学生解决数学问题的利器。活用数形结合思想能使学的抽象思维和形象思维结合起来,从而形成一种解题的思想意识。纵观多年来的高考试题,巧妙运用数形结合的思想方法解决一些抽象的数学问题,可起到事半功倍的效果,我们要让学生体会到数形结合思想的妙用与奇效。下面我们例举数形结合思想方法的各种运用。
1.利用数形结合思想解决不等式问题
例.【2003全国理】设函数f(x)={若f(x0)>1,则x0)的取值范围是( )。
A、(-1,1)
B、(-1,+∞ )
C、(-,-2)(0,+)
D、(-,-1)(1,+)
分析:本题主要考查函数的基本知识,利用函数的单调性解不等式以及考生借助数形结合思想解决问题的能力。
一般解法:解得x<-1或x>1(难解、易错)。 解法2(数形结合):如图1,在同一坐标系中,

作出函数y=f(x)的图象和直线y=l,它们相交于(-1,1)和(1,1)两点,因为f(x)>1由图得 x<-1 或 x>1。
2.利用数形结合思想解决方程解的个数问题
例.方程 lgx=sinx的实数根的个数是( )。
A 1 个 B 2个C 3个 D 4个
分析:本题用代数的方法求解该方程
是很困难的,故考虑用数形结合法,方程的解是函数y=lgx与y=sinx图象的交点的横坐标。在同一坐标系里作出两函数的图像,如右图,看出两个图象有三个交点,故方程有三个解故选C。

3.利用数形结合思想代数问题转化为直线斜率问题


例.【1990年全国理】如果实数x、y满足等式(x-2)2+y2=3,那么的最大值是( )则 y=xk 代入方程由判别式大于等于零得解。采用数形结合思想方法来做,可以立竿见影:方程 (x−2 )2+y2=3
分析:代数方法很繁琐:令表示坐标平面上以为(2,0)圆心,为半径的圆(如上图)。而则表示圆上的点(x,y)与坐标原点(0,0)的连线的斜率,如此以来,该问题可转化为如下几何问题:动点A在以(2,0)为圆心,以为半径的圆上移动,求直线OA的斜率的最大值,由图知当点A在第一象限,且与圆相切时,OA的斜率最大,口算即得最大值为,故选D。
4.利用数形结合思想解求参数取值范围问题
1.若关于x的方程x2+2kx+3k=0的两根都在-1和-3之间,求k的取值范围。
分析:一元二次方程根的分布从“形”的角度很难理解,但采用数形结合思想来做则很直观,令f(x)=x2+2kx+3k=0则其图像与横轴交点的横坐标就是原方程的根。由下图可知要使方程两根分布在-1和3之间,只需
同时成立,解得:
−1 “学而不思则罔,思而不学则殆”,我们在教学中不仅要教会学生数学知识、技巧、方法,更重要的是引导学生学会反思、总结,提炼数学思想。其实技巧只是解决问题的特殊手段,方法是解决一类问题的共同手段,而思想是方法的升华。所以最高层的是数学思想,所以我要引领学生认真反思、总结把学生学生的思维能力、数学能力提升到一个更高的层面。如果学生不会反思、总结解题的方法、技巧、以及所用的思想方法,那他们一定学不好数学,永远是模仿,或掌握的是解题技能,方法,而无法领悟到解觉数学问题最深层的精灵——数学思想。数形结合思想方法是高中数学中最重要是数学思想,运用广泛,贯穿整个高中红数学学习的始终。那么数形结合思想在高中数学教学中的渗透、运用、总结、提炼、升华显得尤为重要。它在数学学习、运用中的作用在我国数学家华罗庚先生的诗中得以充分印证:“数形本是相倚依,焉能分作两边飞。数缺形时少直觉,形少数时难入微。数形结合百般好,隔离分家万事休。几何代数统一体,永远联系莫分离”。所以我们在教学中一定要加大引导学生总结、反思的力度,让数形结合思想方法在学生头脑中生根、发芽、开花、结果。 总之,在数学研究和学习中,数是形的抽象概括,形是数的直观表现。数与形的结合,一方面是通过数量关系的讨论来研究几何图形的性质,像解析几何、立体几何(向量法)这些知识就是建立在这种思想方法的基础上。用代数方法统一处理几何问题,成为现在数学的先驱。几何问题代数化,这乃是数学的一大进步。我们说“数形结合”是发挥数与形的双重优越性,而不是几何取代代数;另一方面是利用几何图形的直观,揭示数量关系中许多深刻的特性。数形结合的思想方法,是研究数学问题的一个基本方法,深刻理解这一观点,并在我们的教学中注重渗透,灵活运用,强化训练,反思总结,注意提炼升华,形成解题思维,有利于提高学生发现问题、分析问题和解决问题的能力,有利于够迅速提升学生的数学能力。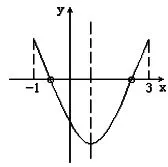
三、注重“反思、总结”的作用,提高学生的数学能力

