基于CVaR两步核估计量的投资组合管理①

黄金波， 李仲飞， 姚海祥

(1. 广东财经大学金融学院， 广州 510320； 2. 中山大学管理学院， 广州 510275；3. 广东外语外贸大学金融学院， 广州 510006)

基于CVaR两步核估计量的投资组合管理①

黄金波1， 李仲飞2*， 姚海祥3

(1. 广东财经大学金融学院， 广州 510320； 2. 中山大学管理学院， 广州 510275；3. 广东外语外贸大学金融学院， 广州 510006)

摘要:在不做任何分布假设的条件下，利用非参数核估计方法对风险度量条件风险价值(conditional value-at-risk, CVaR)进行估计，得到CVaR的两步核估计公式.然后用估计出来的CVaR代替理论上的CVaR建立均值-CVaR模型，实现对风险估计与投资组合优化同时进行，并基于迭代思想设计求解该模型的简单算法.蒙特卡洛模拟结果表明基于两步核估计方法的投资组合优化模型和算法比现有的方法更加有效，估计出来的组合边界误差更小.引入无风险资产后，文中的模型和算法同样适用.最后，为说明其应用价值，采用中国A股市场的日收益率数据进行了实例分析.

关键词:均值-CVaR模型； 两步核估计量； 组合边界； 中国A股市场

0引言

投资组合选择的定量分析可追溯到Markowitz[1]建立的均值-方差模型，此后，均值-风险框架成为现代投资组合选择理论的基本分析框架之一.用期望收益率度量投资收益已被广泛接受，然而，以收益率的方差作为风险度量指标，则受到多方面的批评.许多学者在批判方差的基础上发展了多种风险度量工具，从而推动了现代投资组合选择理论的发展.风险价值(value-at-risk，VaR)和条件风险价值(conditionalvalue-at-risk，CVaR)风险度量正是在这个背景下被提出并很快被运用于投资组合选择和风险管理研究中.VaR是指给定置信水平下某一个资产或资产组合在未来一定期限内的最大可能损失[2].由于VaR不满足一致性风险度量理论的次可加性公理[3-4]，从而破坏投资组合理论中的风险分散化原理.另外，VaR不能对超过VaR水平的损失给出任何信息.所以在VaR基础上，Rockafellar和Uryasev[5-6]给出了CVaR的概念.CVaR度量的是损失超过VaR水平的条件期望值.CVaR满足一致性风险度量要求，弥补了VaR不满足次可加性、未考虑尾部风险等缺陷.

VaR和CVaR被提出之后，对它们的研究沿着两个方向展开，一个是VaR和CVaR估计问题的研究，另一个是基于均值-VaR和均值-CVaR模型的投资组合优化问题研究.一直以来，这两个方向的研究相对独立发展.风险估计问题的研究注重开发更加精确的计量模型和方法来捕捉金融市场的特征，进而更加准确地估计金融市场风险，目前这方面的研究已相当完备，并始终处于不断发展中.相对而言，因VaR和CVaR的优化问题较难处理，基于VaR和CVaR的投资组合研究大多在特定分布下进行，这使得投资组合选择理论的应用受到局限.

关于均值-VaR模型和均值-CVaR模型较为成熟的研究大多在正态(或椭球)分布假设下进行[7-8].在正态(或椭球)分布的假设下，VaR和CVaR可以表达成均值和方差的线性函数，均值-VaR模型和均值-CVaR模型退化成均值-方差模型[5]，而均值-方差模型的研究已经相当成熟.所以，在正态(或椭球)分布假设下，VaR和CVaR与方差在风险度量方面没有本质区别，这将无法凸显VaR和CVaR在风险度量方面的优越性.另外，在实际的金融市场上，金融时间序列数据通常表现出尖峰厚尾、非对称等非正态(或椭球)分布特征，简单的正态(或椭球)分布假设将会导致风险估计的系统偏差，进而会误导投资者，使得人们无法进行有效的风险管理和组合优化.因此，在不做任何分布设定的条件下，如何利用计量方法估计出现实金融市场中的实际风险，进而把实际风险嵌入到投资组合优化模型中进行投资决策是非常有意义的课题.

针对VaR和CVaR的估计问题，理论界提出了很多方法.Engle和Manganelli[9]将它们分为3大类.第1类是参数法，主要包括GARCH族模型和Copula函数法.第2类是半参数法，主要包括极值理论EVT(extremevaluetheory)和条件自回归VaR.第3类是非参数法，主要包括经验分布函数法和核估计方法.参数法与半参数法都假设收益率(在极值理论下是尾部收益率)服从某一事先设定的模型，然后估计出模型中的参数，进而得到风险度量VaR和CVaR的估计值[10-11].相对于参数法与半参数法，非参数法不需要对收益率做任何形式的模型设定，避免人为的模型设定风险和参数估计偏差，能够给出较为准确的风险估计.更重要的是，非参数核估计方法允许金融时间序列之间相互依赖[12-13]，Bellini和Figa-Talamanca[14]证实收益率序列数据显示出非常强的尾部依赖，而参数法与半参数法对于这类相互依赖变量问题的处理较为棘手[12].

近年来，非参数核估计法因具备上述几方面的优势而备受广大学者关注.利用核估计法估计金融风险始于Gourieroux等[15]的研究，他们首次考察了VaR的核估计.随后Scaillet[16-17]把核估计法应用到对期望损失(expectedshortfall，简称ES)*在分布函数满足连续性的条件下，ES与CVaR是同一个风险度量指标的两个不同称呼.的估计.Scaillet[16]提出ES的两步核估计法，并用它来估计资产组合的期望损失和期望损失对组合头寸的敏感性.Scaillet[17]研究了条件VaR和条件ES的非参数核估计，并在平稳过程满足强混合条件下，导出了条件ES核估计量的渐进性质.Chen[18]同时用经验分布函数和核平滑分布函数估计ES，得出二者在估计的方差和均方误差方面并无明显的差异.刘静和杨善朝[19]放松Scaillet[16]的前提条件，在α混合序列具有幂衰减混合系数条件下，用两步核估计法估计ES，得到了ES核估计量的Bahadur表示、均方误差和渐近正态性的收敛速度.刘晓倩和周勇[20]比较两步核光滑ES估计与ES完全经验估计及一步核光滑估计的优劣，得到两步光滑化并不能减小ES估计的方差，该发现与Chen[18]的结论一致.由于CVaR的核估计量具有良好的连续性和光滑性，可以方便地处理投资组合优化问题，这一优点是ES完全经验估计不具备的.所以，许多学者倾向于利用核估计法来研究组合的CVaR及相关优化问题[16,21].

虽然近年来，学者对CVaR的非参数核估计法做了诸多研究，但还鲜有学者把CVaR的核估计与风险优化、投资组合选择问题结合起来考虑.问题是不仅需要知道风险有多大，而且还要知道如何去对冲和管理风险，风险估计只是解决了前面的问题，而后面的问题往往更为重要.Yao等[21]对此做了有益尝试，他们利用Rockafellar和Uryasev[5]给出的CVaR特殊表达式并结合非参数核估计方法，得到核估计框架下的均值-CVaR模型，并利用优化算法求解模型得到投资组合的组合边界.不同Yao等[21]的研究，本文直接利用两步核估计方法对CVaR进行估计，并将CVaR的两步核估计式嵌入均值-CVaR模型，这样就不需要借助于Rockafellar和Uryasev[5]的CVaR特殊形式，而且模型的自变量维数比Yao等[21]的少.本文基于迭代思想设计了简单的算法对该模型进行求解.蒙特卡洛模拟结果显示，在偏差意义下，基于两步核估计方法的均值-CVaR模型和算法准确有效，比现有方法的估计误差小*误差指标的定义可见后文的式(19)..最后将模型和算法拓展到存在无风险资产时的情形，并将它们应用到中国A股市场.

1组合风险CVaR的两步核估计

1.1非参数核估计方法基础

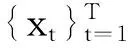
(1)

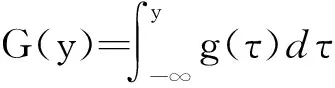
分布函数的核估计量考虑了局部加权平均，在每个点处的分布函数估计值都利用了所有的样本数据，比经验分布函数包含了更多的样本信息.Chen和Tang[12]得出分布函数的核估计量和经验分布函数都是真实分布函数的一致估计量，但前者的方差更小.在核估计中，核函数起到平滑的作用，由于非参数核估计结果对不同的核函数并不太敏感，所以只要满足一定的正则性条件，核函数可由研究者根据问题的不同自由选取.如果是对单变量的密度函数或分布函数进行估计，二阶Gauss核函数能够给出更稳健的结果.所谓二阶Gauss核函数就是g(·)取标准正态分布的密度函数.可以验证二阶Gauss核函数满足前面对核函数的5点要求.通常情况下，非参数核估计方法需要大量的观察数据才能够拟合得比较准确，证券市场上大量的高频数据可以满足这一要求.

1.2组合风险CVaR的两步核估计

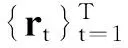
根据VaR的定义，投资组合的VaR数学表达式为

v(x,α)∶=-inf{z:FR(z)≥α}⟹

FR(-v(x,α))=α

(2)

式中FR(·)为R的分布函数，设其连续可导.

根据CVaR的定义，投资组合的CVaR数学表达式为[16]

u(x,α)∶=E[-R|-R>v(x,α)]

(3)

式中fR(·)为R的密度函数，E[·]为期望算子，边际CVaR (marginal CVaR，MCVaR)被定义为组合CVaR对头寸的导数[16]

Δxu(x,α)=E[-r|-R>v(x,α)]

(4)

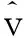
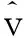
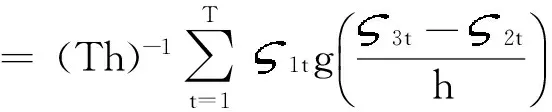
其中g(·)为核函数，h为窗宽，则R的密度函数fR(z)和分布函数FR(z)的核估计量分别为

(5)

(6)

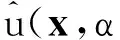
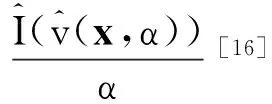
(7)

1.3组合风险CVaR的凸性

引理1[23]组合风险CVaR对组合头寸的二阶导数矩阵的解析式为

V[r|R=-v(x,α)]

(8)

式中p(·)为-R-v(x,α)的概率密度函数；P(·)为它的分布函数；V[·]为方差算子.

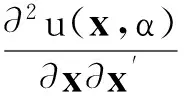
(9)

又

则其核估计公式为*这里用到非参数核估计的回归技术，具体可见参考文献[22]的第60-66页.

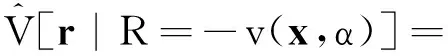
(10)

由此可得二阶导数矩阵的核估计量为

(11)

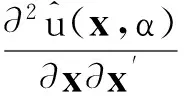
此定理的证明可参见文献[15]和文献[23].

2均值-CVaR模型基础知识

假设存在n(n>1)种风险资产，资产交易无摩擦，市场上不存在卖空限制，投资者的财富标准化为1，其它条件同上.记e为元素全为1的n维列向量，R为投资者要求的最低期望收益率，u为投资者愿意承受的用CVaR度量的最大风险，λ为投资者的风险厌恶系数，均值-CVaR最优化模型可由以下3种方式构建

令参数R,u,λ变动，便产生了各自意义下的均值-CVaR组合边界.Krokhmal等[24]证明在一定条件下，3种模型得到的组合边界是等价的，所以，下文只讨论模型Ψ1.

假设市场引入一个无风险资产，rf为无风险资产的收益率.x=(x1,x2,…,xn)′为投资者在风险资产上持有的头寸，则(1-x′e)为投资者在无风险资产上持有的头寸.投资组合的收益率R=(1-x′e)rf+x′r.根据CVaR的平移不变性[4]，存在无风险资产时组合CVaR为

u(rf,x,α)=-(1-x′e)rf+u(x,α)

(12)

由此，可以建立含有无风险资产时的均值-CVaR模型

2.2正态分布假设下的均值-CVaR模型与显示解

记p=[p1,p2,…,pn]T，q=[q1,q2,…,qn]T，将脉冲控制协议式 (2) 代入系统式 (1) 得

在n(n>1)种风险资产的收益率r服从联合正态分布N(μ,Σ)的假设下，投资组合的CVaR可表达成期望和标准差的线性组合[25]

利用均值-方差的组合边界表达式，可以得出均值-CVaR的组合边界表达式为[25]

(13)

其中A=e′Σ-1μ；B=μ′Σ-1μ；C=e′Σ-1e；D=BC-A2.

在引入一个无风险资产的情况下，均值-CVaR的组合边界方程为[25]

(14)

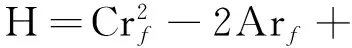
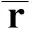
3基于CVaR两步核估计量的均值-CVaR模型

3.1模型与求解

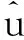
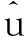
条件1h满足窗宽的估计公式

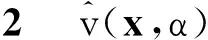
设定Lagrange函数

μ2(x′e-1)

(15)

记y=(x′,μ1,μ2)′，则一阶条件为

其中

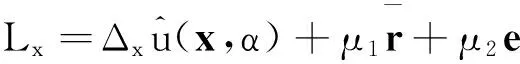
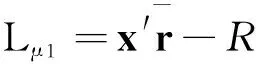
(16)

Lμ2=x′e-1

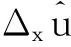
(17)

其中

(18)

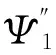
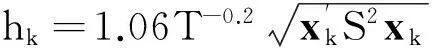
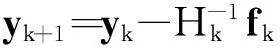
为了保证上面迭代算法能够顺利进行，本文得到以下两个定理.

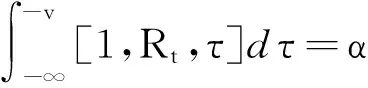
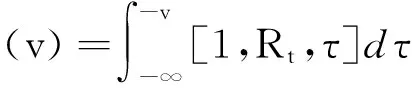
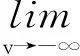
ϑ(v)为严格单调减函数，所以方程ϑ(v)=α有且仅有1个解.

证毕.

定理3如果集合

B={x|x∈

3.2蒙特卡洛模拟

本节给出一些模拟算例，验证3.1节模型和算法的准确性.假设n(n>1)种资产收益率向量r服从n维正态分布N(μ,Σ)，协方差阵Σ正定，则由Cholesky分解得Σ=Q′Q，Q为上三角矩阵.令r=μ+Q′ε，ε为n维标准正态分布，通过简单推导可知r～ N(μ,Σ)，这样通过ε就可以生成多维正态分布N(μ,Σ)的随机数.本文以下模拟数据都通过Cholesky分解法生成.

令μ=(1.0 1.5 2.0)′*需要说明的是，这里的数据是虚拟数据，数据的量纲(或单位)可以是任意的.如果是金融资产的收益率数据，单位为1%或1‰.，

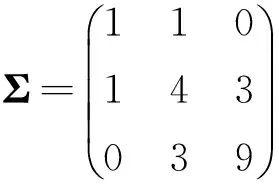
模拟1设定风险资产数量n=3，资产收益率服从正态分布N(μ,Σ)，模拟过程如下.

第1步，采用Cholesky分解生成多元正态分布的样本，取样本容量T= 500，1 000，1 500，2 000，4 000，8 000，设定损失概率分别为1%，5%和10%.

第2步，在每个样本容量和概率下，取30个不同的收益率Ri,i=1,2,…,30，用以下4种方法计算每个收益率对应的最小CVaR.1)把Ri,μ,Σ代入式(13)，得到真实的最小CVaR，记为utrue；2)基于两步核估计框架下的非参数模型和优化算法(记为NP方法)估计出最小CVaR，记为unp,i；3)利用Yao等[21]的模型(记为YL方法)估计出最小CVaR，记为uyl,i；4)基于Rockafellar和Uryasev[5-6]的线性规划方法(记为LP方法)，估计出最小CVaR，记为ulp,i.为比较后3种估计方法的精度，以NP方法为例，定义如下误差指标：绝对误差(absolute error，Ae)和相对误差(relative error，Re), 有

(19)

第3步，重复前面两个步骤40次，即进行40次蒙特卡洛模拟.然后将40次得到的误差指标进行平均，得到平均绝对误差和平均相对误差(见表1和表2).

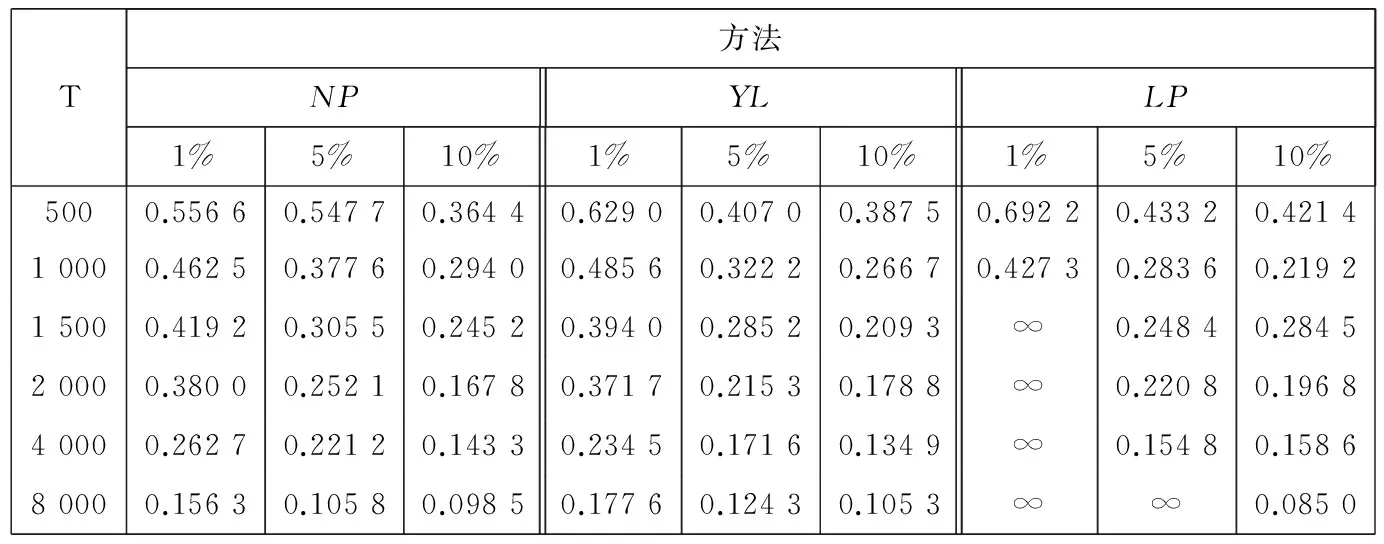
表1　平均绝对误差模拟结果

从表1可以得出以下结论：1)3种估计方法的平均绝对误差都随着样本容量的增加而减小，反映基于3种估计方法得到的组合边界随着样本容量的增加而收敛于真实的组合边界.基于两步核估计方法和YL方法得到的组合边界收敛是因为随机变量的分布函数的核估计量一致收敛于真实的分布函数；2)3种估计方法的平均绝对误差都随着损失概率的增加而减小.这是因为CVaR度量的是损失超过VaR的期望值，各种CVaR估计方法准确性受到质疑的重要方面就是极端风险的样本数据太少，以至不能全面反映尾部分布的特征.α值越大，α分位数以上的样本点越多，从而能够有效利用的数据信息越多，估计也更加准确.另外α值越大，CVaR的绝对数值越小，从而估计的绝对误差也越小是符合预期的；3)从3种估计方法的平均绝对误差的大小来看.3种方法的估计精度相当，在不同的样本容量和损失概率下，各有优劣.但当损失概率较小，比如取1%，或者样本容量较大时，LP方法失效.这是因为LP模型里有n+1+T个自变量，2个等式约束和2T个不等式约束[21]，LP模型里的自变量数和约束方程数随样本容量增加而增加，当样本容量T太大时，LP算法的收敛速度会降低甚至失效(表1和表2中，∞表示优化算法失效).而NP方法的模型里只有n个自变量，2个等式约束，而且随着样本容量T增加，两步核估计方法的估计精度越来越高.YL方法的模型里有n+1个自变量，3个等式约束[21].绝对误差指标没有考虑真值的大小，CVaR的真实值越大，它的估计值与真实值之间的绝对误差也会越大，所以剔除了这种水平效应的相对误差指标更有意义.

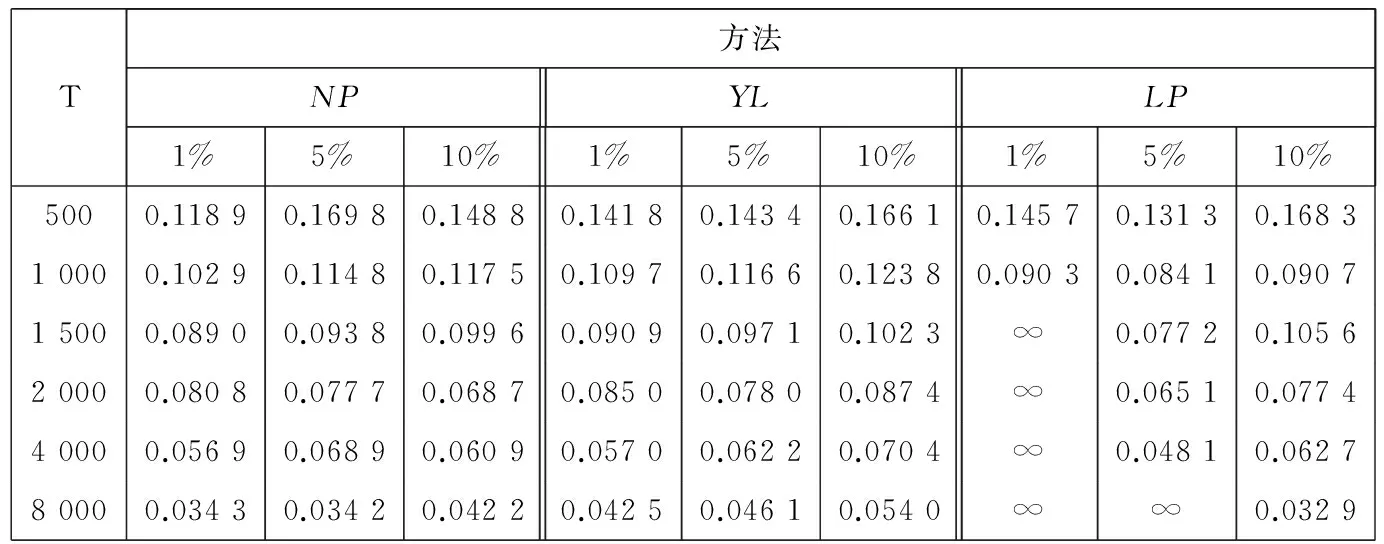
表2　平均相对误差模拟结果

从表2可以得出以下结论：1)同绝对误差指标相同，3种估计方法的平均相对误差都随着样本容量的增加而减小，这说明3种估计方法满足大样本性质；2)除了α=5%,T=500和α=5%，T=4 000外，NP方法的平均相对误差都小于YL方法，说明NP方法的估计精度在大多数时候高于YL方法，这可能是因为NP方法里的自变量和约束条件更少；3)与LP方法相比，NP方法在小概率和大样本情况下表现更好，在实际的金融风险监管和金融机构的风险计算中，通常要计算小概率(小于1%)下的CVaR，所以NP方法在实际应用中更加有效.

限于篇幅，图1仅给出了样本容量为4 000，损失概率为10%时某一次的模拟结果(共模拟40次)，图上直观地显示：基于NP方法得到的组合边界几乎与真实的组合边界重合，而基于YL方法和LP方法得到的组合边界偏差较大.表2的数据也显示样本容量为4 000，损失概率为10%时，NP方法的相对误差(0.060 9)小于YL方法(0.070 4)和LP方法(0.062 7).

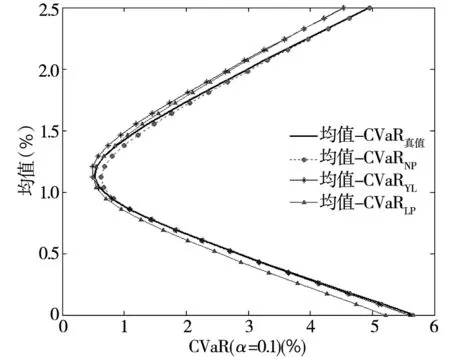
图1　3种估计方法的精度比较

模拟2假设资产数量n=3，资产收益率向量r服从3维t分布tm(μ,Σ)，其中均值μ和散度Σ取值同上，m为自由度，本例取5.设定样本容量为8 000，损失概率为1%，t分布随机数的生成可采用Cholesky分解法*多维t分布随机数的生成过程可见参考文献[26]..本文分别基于NP方法、YL方法和传统方法(记为MN方法)估计多维t分布下的均值-CVaR曲线，并与真实的均值-CVaR曲线比较.在多维t分布的情形下CVaR可表达成均值和方差的线性函数[23]

u(x,α)=-E[R]+kασ(R)

(20)

其中

式中t1-α为自由度为m的经典一维t分布的下1-α分位数；Γ(·)为Gama函数.将式(13)中的φ(zα)/α替换成kα可得到多维t分布下真实的均值-CVaR曲线.

结果见图2.从图中可以得出以下结论：首先，MN方法，即传统方法，是在正态分布假设下将样本均值和样本方差阵代入式(13)得到均值-CVaR曲线的估计，如果真实分布不是正态分布(本例中是多维t分布)，这种方法将是有偏的，图2直观地显示MN方法系统地低估投资组合的风险；其次，对比图1和图2可以发现，在相同的均值向量、方差阵(或散度)和损失概率下，多维t分布下的极端(即小概率下)风险值要大于正态分布，即在相同收益率下，多维t分布下的有效前沿的CVaR更大.第三，NP方法和YL方法估计出来的均值-CVaR曲线与真实的均值-CVaR曲线比较接近，而NP方法的估计偏差更小一些.

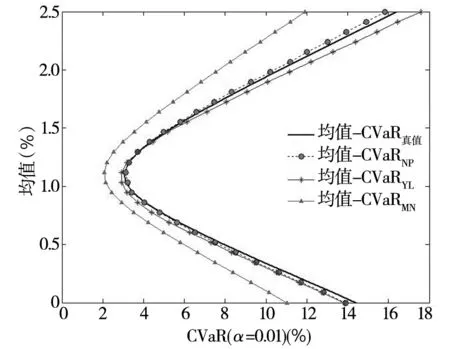
图2　多维t分布下的‘均值-CVaR’曲线估计

本节选取我国A股市场10只股票的日收益率数据进行实例分析，它们是：万科A、深物业A、深深宝A、云南白药、铜陵有色、格力电器、罗牛山、承德露露、新希望和青岛啤酒.数据期间为2007-01-01～2012-12-31，由于在某些交易日，有些股票由于各种原因会停盘，所以必须选出那些每只股票都有交易的交易日收盘价数据，经过删减和匹配处理后，每只股票的可用日对数收益率数据为1 278个.由于日对数收益率数据都很小，为了方便，把所有的日对数收益率数据都乘以100.容易算得10只股票日对数收益率的样本均值和样本协方差阵分别为

本文分别基于传统方法(即MN方法)、NP方法、YL方法和LP方法4种估计方法得到α=5%时的组合边界(见图3).传统方法假设这10支股票的联合分布为正态分布，而另外3种估计方法都不需要对分布进行事前设定.在实践中，事先并不知道这10只股票的收益率服从何种分布，从估计的结果来看，如果这10只股票的联合分布确实服从正态分布，那么传统方法与另外3种方法得到的组合边界趋向一致，图3并没有显示出这种趋势.特别是在组合边界的下半部分，传统方法估计出来的组合边界明显不同于其它3种估计方法得到的结果，而其它3种估计方法得到的组合边界趋向于一致，这也就说明这10只股票的联合分布不服从正态分布.在不服从正态分布情况下，传统方法将是有偏的，它给出的组合边界不是最有效的，也就是说它基于正态分布假设给出的CVaR估计式本身是不恰当的，所以在优化模型里得到的最小化CVaR并不是真正的最小CVaR.

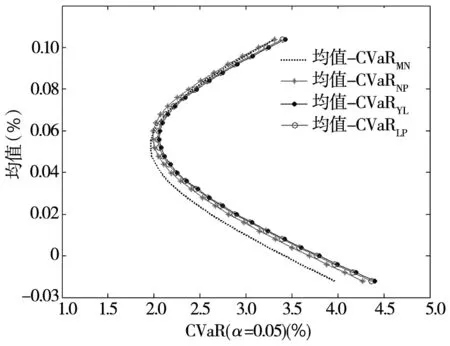
图3　中国A股市场的‘均值-CVaR’曲线估计

4引入无风险资产

4.1模型与求解

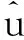
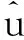
4.2蒙特卡洛模拟

模拟3仿照基于均值-方差模型的资本市场线定义，本文把存在无风险资产时均值-CVaR模型的有效边界定义为资本市场线(capitalmarketline,CML).假设存在3种风险资产和1种无风险资产，风险资产的收益率服从联合正态分布N(μ,Σ)，μ和Σ取值同上.无风险资产的收益率为0.5，取样本容量为4 000，损失概率5%.将真实参数代入式(13)和式(14)可以得到真实的组合边界曲线和CML，基于两步核估计框架可以得到估计出来的组合边界曲线和CML.从模拟结果来看(见图4)，基于两步核估计方法得到的CML和真实CML非常接近，说明利用两步核估计方法对CVaR进行估计是合适的，引入无风险资产后，本文的模型和算法也是可行且准确的.

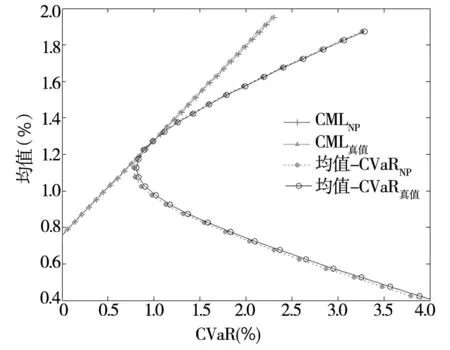
图4　均值-CVaR’曲线和CML(α=5%)

4.3实例分析

继续使用3.3节的10只股票作为风险资产，取无风险资产收益率为1%*由于前面10只股票的日收益率都乘以100，此处无风险资产的日利率取为1%是合适的.，分别估计损失概率为3%和5%时的组合边界曲线与CML.值得注意的是，与基于均值-方差模型的资本市场线不同，基于均值-CVaR模型的资本市场线不过点(0,rf)，而是过点(-rf, rf)*此时所有资产投在无风险资产上，组合的收益率为rf，组合的CVaR为-rf；实际上，当风险资产的收益率服从联合正态分布时，可以从式(14)直接推出这个结论.，模拟结果也证实了这一点，即CML与纵轴交点的纵坐标不是1%(见图5).另外，虽然没有严格的证明，但模拟的结果显示在各自的损失概率下，组合边界曲线和CML相切，这一点说明在非正态分布情况下，CAPM依然成立.最后值得一提的是，这里的估计结果完全是利用样本数据基于本文的两步核估计方法建模并通过简单迭代算法计算得到，不需要任何的分布假设和参数设定，只需要一组样本数据，前面的蒙特卡洛模拟说明这种方法是准确有效的.

图5　中国A股市场的‘均值-CVaR’曲线和CML估计

5结束语

一直以来，金融风险的估计和基于均值-风险模型的投资组合选择理论相对独立发展，本文尝试将二者结合起来，建立一个完整框架实现风险估计与投资组合优化同步进行.近年来核估计方法因具有模型设定灵活、能够抓住金融序列的尾部风险特征、允许数据序列相依等优点，备受国内外学者的关注，是对金融市场风险进行估计的理想方法.本文不需对分布函数做任何假设，也不需要知道CVaR的函数形式，直接利用核估计方法得到CVaR的两步核估计式，进而将CVaR的两步核估计式嵌入均值-CVaR模型，并设计个简单算法对该模型进行求解.蒙特卡洛模拟结果表明基于两步核估计方法的模型和算法得到的结果同已知真实分布情况下的结果高度一致，这要归功于非参数核估计方法能够很好地拟合分布函数.进一步，基于我国A股市场数据的实例分析说明我国金融市场的收益率数据不服从正态分布，基于正态分布假设的投资组合选择模型会误导投资者.

当然，如何结合风险估计和投资组合优化是目前学者思考的前沿课题，本文的研究是初步的.下一步的研究可以沿着两个方向进行：1)将本文核估计框架扩展到其它风险度量指标，如VaR、半方差、下偏矩、绝对偏差、安全首要、EaR、CaR、WCT等；2)放松本文的假设，加入卖空限制、不同借贷利益、存在交易费用等约束，在更加现实的市场环境下拓宽本文的研究.

参 考 文 献：

[1]MarkowitzH.Portfolioselection[J].JournalofFinance, 1952, 7(1): 77-91.

[2]JorionP.ValueatRisk[M]. 2ndEdition.NewYork:McGraw-Hill, 2001.

[3]ArtznerP,DelbaenF,EberJM,etal.Thinkingcoherently[J].Risk, 1997, (10): 68-71.

[4]ArtznerP,DelbaenF,EberJM,etal.Coherentmeasuresofrisk[J].MathematicalFinance, 1999, 9(3): 203-228.

[5]RockafellarRT,UryasevS.Optimizationofconditionalvalue-at-risk[J].TheJournalofRisk, 2000, 2(3): 21-41.

[6]RockafellarRT,UryasevS.Conditionalvalue-at-riskforgenerallossdistributions[J].JournalofBankingandFinance, 2002, 26(7): 1443-1471.

[7]AlexanderG,BaptistaA.Economicimplicationsofusingamean-varmodelforportfolioselection:Acomparisonwithmean-varianceanalysis[J].JournalofEconomicDynamicsandControl, 2002, 26 (7/8): 1159-1193.

[8]姚京, 李仲飞. 基于VaR的金融资产配置模型[J]. 中国管理科学, 2004, 12(1): 8-14.

YaoJing,LiZhongfei.TheassetallocationmodelbasedonVaR[J].ChineseJournalofManagementScience, 2004, 12(1): 8-14. (inChinese)

[9]EngleRF,ManganelliS.CAViaR:Conditionalautoregressivevalueatriskbyregressionquantiles[J].JournalofBusiness&EconomicsStatistics, 2004, 22 (4): 367-381.

[10]林宇, 黄登仕, 魏宇. 胖尾分布及长记忆下的动态EVT-VaR测度研究[J]. 管理科学学报, 2011, 14(7): 71-82.

LinYu,HuangDengshi,WeiYu.StudyonfinancialmarketsdynamicEVT-VaRmeasuringbasedonfated-taildistributionandlongmemoryvolatility[J].JournalofManagementSciencesinChina, 2011, 14(7): 71-82. (inChinese)

[11]叶五一, 缪柏其. 已实现波动与日内价差条件下的CVaR估计[J]. 管理科学学报, 2012, 15(8): 60-71.

YeWuyi,MiaoBaiqi.EstimatingofCVaRwithconsiderationofrealizedvolatilityandpricerange[J].JournalofManagementSciencesinChina, 2012, 15(8): 60-71. (inChinese)

[12]ChenSX,TangCY.Nonparametricinferenceofvalue-atriskfordependentfinancialreturns[J].JournalofFinancialEconometrics, 2005, 3(2): 227-255.

[13]赵晓玲, 陈雪蓉, 周勇. 金融风暴中基于非参估计VaR和ES方法的风险度量[J]. 数理统计与管理, 2012, 31(3): 381-383.

ZhaoXiaoling,ChenXuerong,ZhouYong.RiskmeasurebasedonnonparametricestimateofVaRandESinfinancialcrisis[J].JournalofAppliedStatisticsandManagement, 2012, 31(3): 381-383. (inChinese)

[14]BelliniF,Figa-TalamancaG.Detectingandmodelingtaildependence[J].InternationalJournalofTheoreticalandAppliedFinance, 2004, 7(3): 269-287.

[15]GourierouxC,LaurentJP,ScailletO.Sensitivityanalysisofvaluesatrisk[J].JournalofEmpiricalFinance, 2000, (7): 225-245.

[16]ScailletO.Nonparametricestimationandsensitivityanalysisofexpectedshortfall[J].MathematicalFinance, 2004, 14(1): 115-129.

[17]ScailletO.Nonparametricestimationofconditionalexpectedshortfall[J].InsuranceandRiskManagementJournal, 2005, (74): 639-660.

[18]ChenSX.Nonparametricestimationofexpectedshortfall[J].JournalofFinancialEconometrics, 2008, 6(1): 87-107.

[19]刘静, 杨善朝. 风险度量ES的非参数估计[J]. 工程数学学报, 2009, 26(4): 577-585.

LiuJing,YangShanchao.Nonparametricestimationofexpectedshortfall[J].ChineseJournalofEngineeringMathematics, 2009, 26(4): 577-585. (inChinese)

[20]刘晓倩, 周勇. 金融风险管理中ES度量的非参数方法的比较及其应用[J]. 系统工程理论与实践, 2011, 31(4): 631-642.

LiuXiaoqian,ZhouYong.NonparametricestimationandcomparativeanalysisofESinriskmeasurewithapplications[J].SystemsEngineering-Theory&Practice, 2011, 31(4): 631-642. (inChinese)

[21]YaoHX,LiZF,LaiYZ.Mean-CVaRportfolioselection:Anonparametricestimationframework[J].Computers&OperationsResearch, 2013, 40(4): 1014-1022.

[22]LiQ,RacineJS.NonparametricEconometrics:TheoryandPractice[M].Princeton:PrincetonUniversityPress, 2007.

[23]刘小茂, 李楚霖. 资产组合的CVaR风险的敏感度分析[J]. 数学物理学报, 2004, 24A(4): 442-448.

LiuXiaomao,LiChulin.Sensitivityanalysisofconditionalvalueatrisk[J].ActaMathematicaScientia, 2004, 24A(4): 442-448.(inChinese)

[24]KrokhmalP,PalmquistJ,UryasevS.Portfoliooptimizationwithconditionalvalue-at-riskobjectiveandconstraints[J].JournalofRisk, 2002, 4(4): 43-68.

[25]刘小茂, 李楚霖, 王建华. 风险资产组合的均值-CVaR有效前沿(II)[J]. 管理工程学报, 2005, 19(1): 1-5.

LiuXiaomao,LiChulin,WangJianhua.Mean-CVaRefficientfrontieranditseconomicimplications(II)[J].JournalofIndustrialEngineering/EngineeringManagement, 2005, 19(1): 1-5. (inChinese)

[26]CuiXT,ZhuSS,SunXL,etal.NonlinearportfolioselectionusingapproximateparametricValue-at-Risk[J].JournalofBanking&Finance, 2013, 37(6): 2124-2139.

Investmentportfoliomanagementbasedonthetwo-stepkernelestimatorofCVaR

HUANG Jin-bo1, LI Zhong-fei2*, YAO Hai-xiang3

1.SchoolofFinance,GuangdongUniversityofFinance&Economics,Guangzhou510320,China;2.SunYat-SenBusinessSchool,SunYat-SenUniverstiy,Guangzhou510275,China;3.SchoolofFinance,GuangdongUniversityofForeignStudies,Guangzhou510006,China

Abstract:The paper first applies nonparametric kernel estimation method to estimating CVaR which is currently a popular risk measurement tool, then derives a two-step kernel estimator of CVaR with distribution-free specification. Next, a two-step kernel estimator of CVaR is embed into the mean-CVaR portfolio optimization models to derive financial risk estimation and portfolio optimization at the same time. A simple iterative algorithm is designed to solve these models. Monte Carlo simulation result shows that the portfolio optimization models and the algorithm based on the two-step kernel estimator of CVaR is feasible and effective, and that the estimated error of portfolio frontier is very small. The models and algorithm above apply to a risk-free security. Finally, an empirical analysis of daily return data from Chinese A-stock market is presented to illustrate the application of this research.

Key words:mean-CVaR model; two-step kernel estimator; portfolio frontier; Chinese A-stock market

收稿日期：① 2013-08-17；

修订日期：2014-03-24.

基金项目：国家自然科学基金重点资助项目(71231008)； 国家自然科学基金资助项目(71471045)； 中国博士后科学基金特别资助项目(2015T80896)； 中国博士后科学基金资助项目(2014M562246; 2014M560658)； 全国统计科学研究计划资助项目(2013LY101)； 广东省自然科学基金研究团队资助项目(2014A030312003)； 广东省高等学校高层次人才资助项目； 广东省高等院校科技创新资助项目(2012KJCX0050)； 广东省普通高校特色创新资助项目(人文社科类)； 广州市哲学社会科学规划资助项目(14G42).

通信作者：李仲飞(1963—)， 男， 内蒙古鄂尔多斯人， 博士， 教授， 博士生导师. Email: lnslzf@mail.sysu.edu.cn

中图分类号:F830.9; O212.7

文献标识码:A

文章编号:1007-9807(2016)05-0114-13