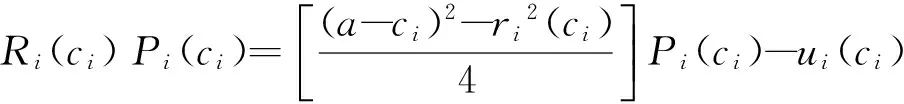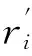技术拍卖的最优机制①
石 岩, 谢富纪, 刘 浪
(1. 南昌航空大学经济管理学院, 南昌 330063; 2. 上海交通大学安泰经济与管理学院,上海 200052; 3. 华东交通大学经济管理学院, 南昌 330013)
技术拍卖的最优机制①
石岩1, 2, 谢富纪2, 刘浪3
(1. 南昌航空大学经济管理学院, 南昌 330063; 2. 上海交通大学安泰经济与管理学院,上海 200052; 3. 华东交通大学经济管理学院, 南昌 330013)
摘要:实践中,技术拍卖常常采用固定费(英式)拍卖,报价与技术的产出无关.把技术的拍卖价格与其产出联系起来,提出了两部制拍卖机制,即获胜者要支付固定费与提成.首先,作为比较基准,分析了固定费拍卖.其次,分析了独立私有价值情形的最优两部制拍卖机制,每个企业直接报告自己的成本,成本最低的企业赢得拍卖.最优拍卖的固定费与提成由企业报告的成本决定,并且无需设定保留价格. 与固定费拍卖相比较,两部制拍卖能够带来更高的期望收益,以及更高的拍卖成交率.
关键词:技术拍卖; 最优机制; 英式拍卖; 两部制
0引言
近年我国政府做出了提高自主创新能力,建设创新型国家的决策,十八大报告中又提出实施创新驱动发展战略.但是长久以来,我国科技成果转化率一直偏低,甚至不到10%,远远低于发达国家.这种状况的存在,不仅使技术大量闲置,造成资源浪费,还严重削弱科技对社会经济发展的支撑作用,影响到现阶段发展战略的实施.
因此,无论政府还是学界,一直努力研究技术从实验室走向企业的途径,为拓宽技术产业化的渠道进行积极探索.技术拍卖这种新的交易形式的兴起,在我国是近三、四年的事情,在国际上也只早了3年左右.2010年底开始,中国技术交易所每年举行1次专利拍卖会,至今已成功举办了3届.2011年,谷歌、黑莓等国际著名公司,参加加拿大北电网络公司6 000项专利组合的拍卖,其中谷歌出价9亿美元,中国的华为、中兴也参与到其中.目前,技术拍卖已经使很多重大发明实现了产业化,正成为科技转化成生产力的重要途径.根据中国技术交易所的介绍,拍卖标的不仅包括各种发明、实用新型专利,还包括专利的申请权.
目前在实践上,技术拍卖基本采用英式拍卖,即由竞拍企业不断叫价,价高者得,以固定价格成交.但是技术作为特殊商品,其价格可以与它的产出联系起来,这与普通商品很不一样.在理论研究中,常常采用“固定费+提成”价格作为技术的一般化定价方式[1],即企业先支付给技术所有人一个固定价格(fixed fee),然后再根据技术的产出支付提成(royalty),是个两部制(二元)价格.在实际操作上也是如此,一些技术转让合同范本上,规定了首期支付的固定费,以及事后的提成.然而,当把技术当作普通商品,采用英式拍卖的时候,企业的报价是固定价格,技术的价格与其事后产出无关.所以,目前技术拍卖的定价方式,与“固定费+提成”一般化定价方式存在鸿沟.事实上,单一的固定费定价,或者单一的提成制定价,都可以看作是“固定费+提成”的特例.就其优劣而言,特例不可能比一般更好.本文以“固定费+提成”作为定价方式,提出了两部制定价的技术拍卖最优机制,赢得拍卖的企业不仅支付固定费,还要根据产出支付提成,这与实践上的英式拍卖完全不同.本文将要证明,这种二元定价的技术拍卖机制,在拍卖期望收益以及拍卖成交率两个方面,都优于实践上采用的英式拍卖.
理论界对于技术拍卖的研究,主要关注配置效率与参与人的出价策略.比如Moldovanu和Sela[2]认为企业在进行价格竞争时,低效企业更有出高价的积极性,能够赢得拍卖,所以标准拍卖将导致无效率.Das Varma[3]认为,虽然价格竞争时,技术拍卖可能导致无效率配置,但是古诺竞争时的配置是有效的.Goeree[4]认为为了获得未来的竞争优势,参与竞拍的企业有传递效率信号的动机,会报出高于技术实际价值的报价.谢非等[5]认为企业传递信号的动机会影响技术的拍卖收益,并导致配置无效率的可能性.
如果得到技术许可的企业可以是多家,Hoppe等[6]讨论了许可数量与竞争程度的关系,认为增加许可数量并不总是导致激烈的竞争.Aniruddha[7]分析了技术拍卖中的保留价格,独家许可、多家许可等形式与保留价格有密切关系,有些时候最优的保留价格是0,事实上无需设定保留价格.另外,对于市场前景存在不确定性的情形,Janssen和Karamychev[8]认为风险态度将决定配置,喜欢冒险的企业会赢得拍卖,并且,垄断市场可能比寡头市场更有效,因为赢得竞标的垄断者是对市场预期最乐观的企业,它选择的市场产量更高且产品价格更低.Nicolás和Vasiliki[9]提出了一个很有趣的增加拍卖收益的方法,发明人可以宣称,如果拍卖不掉,将把技术无偿地公开.由于技术被公布后会加剧竞争,将刺激企业在竞拍中的报价,这样虽然公布技术的威胁不会实施,但可以提高拍卖收益.
以上关于技术拍卖的研究,关注的焦点是发明人与企业、以及企业之间的策略性互动,但就拍卖价格形式而言,均采用一次性支付的方式,即单一的固定费.拍卖后企业支付与技术产出无关的使用费,发明人拿了钱走人,也没有把技术价格与其产出联系起来.
把拍卖价格与拍卖品事后实现的价值联系起来,可以增加拍卖收益,这种定价思想在近年得到了重视,在实践上也得到应用.比如,美国的一些州政府组织的油田拍卖,要求竞拍的公司先支付现金赢得开采权,然后根据油田的产出,支付1/6的收益提成[10].在图书的销售中,作者获得的版税也可以与销售情况相联系,例如享受10%的销售提成[11].
De Marzo等[12]认为只要对股权(或者称为有价证券)价值进行排序,拍卖物品的叫价可以采用股权的形式.股权价值决定于拍卖品实际带来的价值,即使股权份额相同,高效率买方的未来收益高,其股权也更有价值.卖方为了提高拍卖收益,可以增加股权在拍卖总支付中占的比重.他们定义了有价证券的“陡度”这个概念,分析了陡度与拍卖收益的关系.同样,Gorbenko和Malenko[13]也研究了有价证券的拍卖问题.虽然项目的利润难以被证实,但是项目实施后的现金流是可观察且可验证的.他们发现,以现金流作为拍卖价格的依据(可称之为“现金分享制”),与设置保留价格一样,可以降低买方的信息租金.特别是,现金收益分享制可以代替保留价格的作用,有时候用了分享制,就没必要再设置保留价格了(保留价格为0).Cornelli和Felli[14]也采用了现金流决定拍卖价格这一做法,分析了如何拍卖一个公司.与有价证券不同的是,公司需要考虑破产的情况,增加拍卖收益的关键在于有效设置现金流的分享比例.
Abhishek等[15]研究了项目的事后利润可以分享的拍卖,此时项目的事后利润是拍卖价格的影响因素之一.如果项目的价值是私人独立同分布的,与一次性给钱走人的拍卖相比较,无论卖方是风险中性还是风险回避的,对于英式拍卖与二价拍卖,拍卖人使用利润分享拍卖都可以得到更高的收益.基于事后信息,Skrzypacz[16]建立了统一的共同价值模型.这些事后信息包括现金流、债务、提成、期权等,对于拍卖价格形成的方式也各有特点,该模型把相关研究放在了一个框架内.
Mezzetti等[17]为了获得拍卖品的事后价值,采用了另外的办法.他们在拍卖规则中加入了惩罚机制,首先所有的买方都报告拍卖品价值,然后获胜的买方去实施项目,拍卖品的真实价值得以实现.如果其余买方的报告与实现价值不一致,说谎的买家要支付罚款.这样就保证了拍卖前买方诚实报告,新的拍卖规则抽取了买家所有的剩余.
葛如一和张朋柱[18]分析了互联网环境下,技术创新外包的悬赏制和招标制.如果技术开发无需很大的投入,并且其产出随机性较大,则悬赏制是适用的,反之则需要进行招标.事实上,这两种机制都是特定条件下的技术拍卖.
文献[12—18]中把拍卖价格与事后价值相联系的做法,对本文的两部制定价的技术拍卖有重要启发.但是这些文献分析的是具体的拍卖形式,即英式拍卖、一价密封拍卖等的均衡结果,本文则着眼于分析最优拍卖机制.从理论上讲,具体的拍卖形式可以有无数种,最优拍卖机制则更有根本性.
本文提出的“固定费+提成”的技术拍卖,也可以看作打分制的一个特例,即发明人要同时兼顾一次性现金收益,与未来能够分享的收益两部分的“分值”之和.拍卖理论的重要分支之一是多目标拍卖,这时需要对多目标综合打分,以分值最大化为目标函数求解拍卖问题.打分制最早由Che[19]提出,分析了拍卖要兼顾物品质量与价格的情形,证明了打分制下的收益等价原理.Cachon和Zhang[20]认为,招标方不仅要考虑价格,而且要考虑时间成本,并分析了两种具体的简单机制,一是耽误时间要赔偿,二是规定一个固定的交付时间,均可以达到较优的拍卖效果.王宏等[21]认为在拍卖前,是否对评分规则的承诺对拍卖期望收益没有影响,只要找到合适的评分规则即可.
关于如何更好地对技术进行定价,Sen[22]假定企业的成本存在信息,分析了只有一个企业购买技术,且信息是两点分布的情况.“固定费+提成”的定价方式可以有效实现信息甄别,优于单一的固定费合同,并对定价合同的多样性进行了解释.仍然只有一个企业作为买方,岳贤平等[23]基于不同的理论框架,分析了两点分布的类似问题,石岩[24]分析了企业的类型是连续分布的情况.一般而言,基于两点分布的分析,能够得出连续分布时的大部分结论.本文仍设企业的成本存在信息,使用Sen的分析框架,但是研究的问题是多个企业参与竞争的技术拍卖,而不是一对一的交易.
1模型描述
一个发明人拥有一项技术,使用此项技术可以生产一种新产品.发明人不参与生产经营,其收益来自技术转让,希望拍卖该技术,其目标是获得尽可能多的技术拍卖收入.另外有n家企业参加竞拍,它们是该技术潜在的买者.发明人对该项技术进行拍卖,只有1家企业能够赢得拍卖得到技术,然后生产这种新产品.设发明人与企业都是风险中性的,且新产品的逆需求函数是线性的,即
p=a-q
其中p、q分别是产品价格与产量,由生产企业决定;a是给定的常数,表示市场规模.考虑竞拍者风险态度时,一般分析中用特定形状的效用函数描述风险态度,但是大多数时候,难以得到有意义的解.王明喜和刘树林[25]定义了风险指标,不仅能够同时描述风险偏好、风险中性与风险规避这3种情况,而且可以得到简洁的结果.
假定由于工艺水平等原因,这n家企业具有不同的边际成本,分别是c1,c2,…,cn.为了后续讨论的方便,设这些企业中,边际成本的最小值是c1,次小值是c2.相应地,效率最高(边际成本最小)的企业,称之为是企业1;效率次高的企业,称为企业2.

每个企业的边际成本都是私人信息,共同知识是分布函数和参加拍卖的人数n.亦即,只有企业i知道自己的边际成本ci的大小,发明人与其他企业都不知道ci,但是知道ci是个随机变量以及其分布函数G(·).事实上,如Sen的做法,本文考虑的是企业成本存在信息的情况.在以上假设中,由于这些企业的边际成本不一样,技术对每个企业具有不同的价值.所以,本文所分析的技术拍卖,可以归于独立同分布私人价值拍卖模型(SIPV模型).
2固定费拍卖
在我国近年的实践当中,技术拍卖照搬了普通物品的拍卖方式,一般采用英式拍卖,也就是由所有的竞拍者不停的加价,价高者得.比如甲报价3万元,乙再报价4万元,最后丙报价5万元.若无人继续加价,则丙赢得拍卖,得到技术并支付报价5万元.由于实践上的这种英式拍卖,获胜者仅支付一个固定价格,称为固定费拍卖.
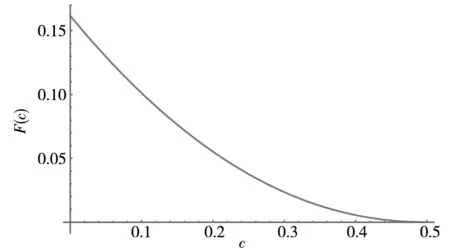
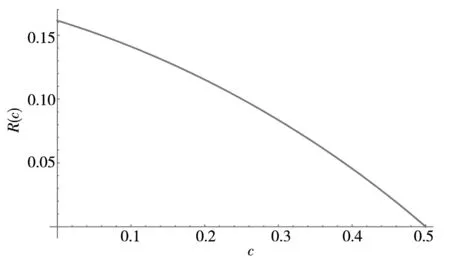
固定费拍卖很容易分析.根据收益等价原理,当技术拍卖使用固定价格时,发明人的期望收益,与采用何种拍卖方式没有关系.除了英式拍卖,若采用其他的3种基本拍卖方式,即降价拍卖、密封一价与二价拍卖,均得到相同的期望收益.于是,可以只分析英式拍卖,作为后面两部制拍卖的比较基准.事实上,仅需得出技术对于企业的私人价值,即可确定拍卖的成交价格.对于拍卖能够完成的情况(没有流拍),因为边际成本是c的企业获得技术后,目标是

企业的边际成本越高,技术对它的价值越低.大家知道,英式拍卖的结果是,成本最低的企业1赢得拍卖,同时成交价格是所有企业私人价值的第二高的价值,或者等于发明人设定的保留价格.其中第二高价是
(1)
为了得到更高的期望收益,发明人可能需要设定保留价格R(c*A).此处保留价格对应的成本c*A,称为保留成本.为了使分析有现实意义,设c1≤c*A≤ch.本文后面的部分,下标“A”代表固定费拍卖,下标“B”表示后面的两部制价格拍卖,以方便相互区别.
2.1期望收益
固定费拍卖的成交价格是R(c2),或者R(c*A),决定于c2和c*A的大小关系.以下分两种情况,讨论企业支付的价格.一是当c2 h(c)=(n-1)[1-G(c)]n-2g(c) 二是当c2≥c*A,此时保留价格具有提高成交价格的作用,对发明人有利.赢得拍卖的企业1,将不得不支付保留价格R(c*A),而不是第二高价R(c2).其中保留价格是 同时相应的概率是 Prob[c2≥c*A]=1-H(c*A)=[1-G(c*A)]n-1 综合以上两种情况,发明人的期望收益是 (2) M(c,c*A)表示给定保留成本c*A,发明人从成本是c的企业获得的拍卖收益.由于成本c是随机变量,M(c,c*A)也是随机变量.对M(c,c*A)在区间[0,c*A]上做积分,就得到发明人从该企业获得的期望拍卖收益.由于事前所有n家企业是对称的,发明人获得的拍卖期望总收益,是从单个企业获得收益的n倍,这也是采用固定费拍卖方式的期望收益.用TA(c*A)表示这个总收益,有 (3) 进行分部积分(见附录1),化简得到 [1-G(c)]n-1g(c)dc (4) 2.2拍卖成交率 由上式的期望收益很容易确定固定费拍卖的保留成本.取式(4)中的积分项为固定费拍卖的虚拟价值,表示为 因为假定分布函数G(·)具有不变的单调风险率特征,虚拟价值Y(c)是单调减的,若方程Y(c)=0在c∈[0,+∞]上有唯一的解,设这个解是c=c0A,由此得到 (5) 若c0A Prob[c1≤c*A]=1-[1-G(c*A)]n (6) 若c0A≥ch,则虚拟价值Y(c)在区间[0,ch]上总是正的.所以,为了最大化拍卖收益,取式(4)的积分上限c*A=ch,此时无需设定保留成本,也无需设定保留价格,而拍卖的成交率是100%.总结以上得到 命题1若采用固定费拍卖,拍卖期望收益是式(4),并且可能需要设定保留价格. 3两部制最优拍卖 本节分析两部制定价的技术拍卖,这要求赢得拍卖的企业支付的技术价格采用“固定费+提成”的形式.无论在理论研究还是实践上,技术的两部制定价方式都极为常见.固定费也称入门费,是企业为了使用技术而支付的与产出无关的费用,提成费则依赖于技术的产出.本文采用最常见的按产量提成,要求每卖出1件产品,企业支付1单位的费用.为方便与固定费拍卖区别与比较,把这种拍卖称为两部制拍卖.以下本文只关注两部制拍卖的基本配置问题,直接分析其最优拍卖机制,即在满足激励相容和个体理性的约束下,能够最大化发明人期望拍卖收益的机制. 为了找到最优拍卖,把两部制拍卖看作机制设计问题.根据Myerson的显示原理,任何一种拍卖的任何一个均衡,可以从获胜概率和预期支付都相等的直接拍卖中得到.如果一种拍卖在激励相容的直接拍卖中是最优的,那么它在所有类型的拍卖中必然也是最优的.因此,在寻找最优拍卖时,只分析激励相容的直接机制即可,这就使问题大大简化.因为在本文中,企业的私人信息是它们各自的边际成本,所以本文的直接机制,要求参与竞拍的企业直接报告其边际成本.拍卖结束后,获胜企业需要支付的价格采用“固定费+提成”的方式,由企业的报告信息,即它报告的边际成本计算得出.设获胜企业的成本是c,在激励相容的机制下,报告成本也会是c,则支付给发明人的技术价格是 R(c)=F(c)+r(c)q(c) (7) 上式即两部制价格函数,其中F(c)是固定费,r(c)是按产量提成的系数,q(c)是技术产业化后企业的实际产量.这样获胜企业的支付R(c),就成为企业成本的函数,拍卖价格也与技术的产出q(c)联系起来了.另外,设竞拍失败的其他企业不支付任何费用. 本文规定拍卖的行动时序是:1)每个企业获知自己的边际成本ci;2)为最大化拍卖所得,发明人宣布拍卖机制;3)所有竞拍企业各自不公开地报告自己的边际成本ci;4)根据机制兑现各方收益. 其中,拍卖机制包括分配规则pi(c1,…,cn)、获胜企业的支付价格R(·),以及发明人设定的保留价格(如果必要的话).分配规则pi(c1,…,cn)决定了竞拍企业赢得拍卖的概率,取决于所有企业的报告成本;R(·)包含了固定费项F(·)与提成r(·),既是获胜企业的支出,也是发明人的拍卖收益;最后,与前面的固定费拍卖类似,两部制拍卖可能需要设定保留价格,以保证收益不理想时,发明人有拒绝出售技术的权利.两部制拍卖的保留价格表示为R(c*B),对应的保留成本为c*B.当c1>c*B,即所有企业的成本都高于c*B时,拍卖无法完成. 以上两部制拍卖使用的直接机制,与把技术当作一般商品的固定费(英式)拍卖,在价格形成方式上明显不同.固定费拍卖要求竞拍企业报出其愿意付出的具体价格,只要最高报价高于保留价格,双方即可成交.两部制拍卖要求企业报告自己的成本,再由式(7)的函数R(·)算出获胜企业要支付的价格,而不是直接报出愿意支付多少钱,保留价格R(c*B)也是按保留成本c*B算出的. 由于企业的成本是私人信息,要求直接报出成本的两部制拍卖是直接机制,而拍卖时要求企业报出价格的固定费拍卖是间接机制,虽然企业愿意支付的价格依赖于各自的成本. 3.1最优机制的解 对两部制拍卖的最优机制进行求解.首先考虑分配规则,由于至多只有1个企业会赢得拍卖,分配规则必须满足可行性条件(FC),这要求 (8) 同时由于可能需要设置保留成本c*B,若所有企业的成本都高于c*B,技术无法拍卖出去,留在发明人手中,所以先用c*B作为积分上限以代替ch.在后面部分,再对其取值作进一步分析.以Pi(ci)表示拍卖前(事前)企业i赢得拍卖的概率,如果其他企业都说真话,同时企业i诚实报告成本是ci,则Pi(ci)表示为 (9) 如果企业i诚实报告边际成本的真实值,将以概率Pi(ci)赢得拍卖,获得技术,生产产品并按照价格函数式(7)支付固定费与提成.给定价格函数ri(ci)与Fi(ci),从事前看来,企业付给发明人的技术使用价格是 Ri(ci)Pi(ci)=[ri(ci)qi(ci)+Fi(ci)]Pi(ci) 企业i以概率Pi(ci)获得技术以后,在产业化阶段,目标是选择产量qi(ci),最大化其期望收益ui(ci). ui(ci)等于企业的市场收入减去技术使用价格 ui(ci)=[a-qi(ci)-ci]qi(ci)Pi(ci)- Ri(ci)Pi(ci) (10) ui(ci)也是企业i获得的信息租金.发明人不能强迫企业参加拍卖,需要保证企业有利可图,参与约束条件(IR)是 ui(ci)≥0,i=1,2,…,n (11) 由式(10)利用最大化ui(ci)的一阶条件,得到企业i在产业化阶段的最优产量是 (12) 把上式代入式(10),企业i与发明人的收益之和是 ui(ci)+Ri(ci)Pi(ci)= (13) 此即技术产业化后,双方获得的总期望价值,也是拍卖交易后的总期望价值.同时由式(13),企业i的信息租金改写成 (14) 以上是企业i诚实报告其成本的结果.但是考虑到企业可能不说真话,比如它真实的成本是ci,参与竞拍时却报出成本是xi(谎报),以求获利.这时候,企业i赢得拍卖的概率以及要支付的技术价格,都决定于它所宣称的成本xi,而与真实的成本ci无关,所以当企业i谎报其边际成本是xi时,将以概率Pi(xi)赢得拍卖,同时支付技术价格 Ri(xi)=ri(xi)qi(ci,xi)+Fi(xi) 但是在产业化阶段,企业i仍然会按照实际的成本ci从事经营.因此当实际的边际成本是ci,而企业报出xi时,与式(14)类似,企业i的收益可以表示为ui(ci,xi),即 (15) 另外,式(14)可看作当企业i的成本为ci,同时竞标时也报出ci(诚实报告)的收益,于是u(ci)可以写成ui(ci,ci).本文考虑的两部制最优拍卖机制,必然是激励相容的,也就是每个企业都有积极性诚实地报告边际成本,构成贝耶斯——纳什均衡.所以当其他的企业都讲真话时,如果企业i也诚实报告,要求说真话对它更有利,激励相容条件(IC)表述为 ui(ci,ci)≥ui(ci,xi) (16) 这意味着关于xi的函数ui(ci,xi)要在xi=ci处达到最大值.必要(一阶)条件是 在后面对最优机制进行求解后,将验证式(16)的确是成立的(见附录2).由以上必要条件可以推出(见附录3) (17) 在后面的求解中,用式(17)替代式(16).根据导数的符号,很容易判断ui(ci)的增减性.由式(12),以上微分式事实上是企业i选择的产量与它赢得拍卖概率的乘积,所以 即激励相容约束成立时,企业的收益ui(ci)(信息租金)是随其成本ci的增加而递减的.只有这样,成本低的企业才有积极性说实话,不会冒充高成本企业以求获利.因此,只要在ci=c*B满足参与约束条件,式(11)就是成立的.所以式(11)可以改写为 ui(c*B)=0,i=1,2,…,n (18) 由于ci是分布在区间[0,ch]上的随机变量,且完成拍卖要求ci≤c*B.取积分上限是c*B,发明人从企业i获得的事前期望收益是Ri(ci)×Pi(ci)在这个区间上的定积分.另外,从企业i获得的期望拍卖收益,是保留成本c*B的函数,用Si(c*B)表示,有 (19) 于是,发明人的最优拍卖机制是选择支付函数和分配规则,在可行性条件、参与约束与激励约束条件下,最大化拍卖期望收益.其中两部制的拍卖期望收益是从所有n家企业获得的期望收益之和,表示为TB(c*B).表述为下面的最优化问题 (20) 对以上问题求解,首先利用式(13),发明人从企业i获得的期望收益是 (21) 考虑到G(0)=0以及ui(c*B)=0,并考虑激励相容式(17),对上式中第二项做分部积分,得 (22) 将式(22)代入式(21)得到 Pi(ci)g(ci)dci (23) 由欧拉方程,最大化Si(c*B)要求 所以对发明人而言,最优的提成系数是 (24) 因为单调风险率成立,所以提成系数ri(ci)是ci的增函数.下面来确定分配规则,将式(24)代入收益函数式(23),成立 Pi(ci)g(ci)dci (25) 利用式(24),定义式(25)积分中的表达式 (26) 上式为发明人的边际收益,也是技术对企业的虚拟价值.大家知道,完全信息时(即发明人可以直接观察到企业成本),发明人可以得到产业化后的全部剩余,边际收益将是(a-ci)2/4.同时,发明人的期望收益将是边际收益在成本ci所在分布区间上的积分.但是由上式可以看出,在拍卖中由于信息不对称,发明人的边际收益会下降. 对发明人而言,从企业i获得的“固定费+提成”收益的期望值,等价于企业i的虚拟价值的期望值.把发明人从所有n家企业获得的期望收益求和,就得到了采用“固定费+提成”的拍卖,即两部制最优拍卖的期望收益.把式(9)、式(26)代入式(25)并求和,拍卖总收益TB(c*B)表示为 (27) 利用上式可以确定最优分配规则.先判断虚拟价值的增减性,对Xi(ci)求导得到 (28) 即发明人应该把技术卖给成本最低的企业,也就是与高效企业合作才符合发明人的利益,这是符合人们的直觉的.事实上,对于上述分配规则还可以换一种解释:在式(27)里面,对于发明人的期望收益,每个企业的分配概率可看作其虚拟价值的权重.发明人为了最大化拍卖期望所得,在拍卖可以完成的情况,要求选择虚拟价值最大者,即成本最低者的权重为1. 由式(28)可以确定企业在事前赢得拍卖的概率.对于边际成本是ci的企业i,在激励相容的机制下,因为所有企业都说实话,成本最低的企业才能获得技术,那么拍卖前企业i获胜的概率是 Pi(ci)=[1-G(ci)]n-1 (29) 另外,虚拟价值是通过计算积分得到的等价概念,它并不是技术拍卖的真实成交价格.本文所分析的最优技术拍卖,仍然需要给出获胜企业的支付函数.也就是一旦赢得拍卖,边际成本为ci的企业需要支付给发明人的具体价格Ri(ci).首先考虑企业的信息租金,对式(17)求积分得到 (30) 由式(13),得到企业付给发明人的支付函数是 [1-G(x)]n-1dx (31) 上式是“固定费+提成”之和,亦即企业给发明人的总支付函数,是与产出相结合的技术拍卖价格.对于拍卖成功的情况,由于边际成本最低的企业赢得拍卖,拍卖的最终成交价格是R(c1). 当采用“固定费+提成”的技术定价方式,实践上有时要求企业先支付固定费部分,在技术产业化后,再根据实际产量支付提成.这样,可以避免企业在投产初期因为购买技术而占用大量资金,对缓解资金压力有积极意义,特别有利于中小型科技企业的发展.这时,就需要分别得出固定费与提成项.本文分析的是按产量提成的情况,最优的提成系数事实上已经由式(24)给出,乘以产业化以后的实际产量,就得到拍卖价格的提成部分,下面只需要再给出固定费项.把信息租金式(30)代入式(14),得到获胜企业需要先支付的固定费是 (32) 3.2期望收益 接着,需要得出发明人使用以上最优两部制拍卖所能得到的期望收益.因为成本最低者(企业1)获得拍卖,对企业1的虚拟价值求积分,即可得到发明人期望收益.把企业1的边际成本c1看作n家企业成本的最小顺序统计量,考虑拍卖可以完成的情况,c1∈[0,c*B],分布密度是n[1-G(·)]n-1g(·).于是对于两部制拍卖,发明人的期望拍卖收益是 (33) 上面结果也可由式(25)直接得到.只需要把获胜概率式(29)代入式(25),就得出发明人从1家企业得到的期望收益.由于拍卖前所有n家企业都是对称的,对发明人来讲每个企业都没有区别,所以从任何一家企业获得的期望收益都一样.式(25)乘以n,就是发明人总的期望拍卖收益,得到式(33). 3.3保留价格 与技术的固定费拍卖一样,两部制拍卖或许需要设定保留价格.如果发明人觉得没有任何一家企业的出价符合预期,可以拒绝出售技术.下面分析在本文的框架下,当技术拍卖采用两部制定价,设置保留价格是否必要.本文的直接机制中,要求企业直接报出自己的边际成本,赢得拍卖企业的成交价格由式(31)而定.发明人通过选择两部制拍卖的保留成本c*B,来确定保留价格R(c*B).下面讨论如何进行选择. 根据式(33),通过选择c*B最大化期望拍卖收益TB(c*B).虽然式中的虚拟价值X(c)是个完全平方式,它总是非负的,但是考虑到企业赢得拍卖后,由式(12),产业化阶段的产量为 (34) 由于产量q(c)随成本c单调递减,为了保证产量是正值,保留成本c*B不能无限制的提高.令c0B是以下方程的解 (35) 与式(5)类似,若上述方程有唯一解,分两种情况讨论: 情况1若c0B Prob[c1≤c*B]=1-[1-G(c*B)]n (36) 情况2若c0B≥ch,由于式(33)中的虚拟价值X(c)总是正的,同时在边际成本的分布区间[0,ch]上,式(34)产量为正,总是能够满足的.所以发明人为了追求拍卖收入,最大化式(33)要求取积分上限c*B=ch,此时事实上无需设定保留成本,自然也无需设定保留价格.并且容易看出,技术拍卖总能够成功,两部制拍卖的成交率是100%. 总结以上结果,得到如下命题 命题2若采用“固定费+提成”的两部制定价方式,最优拍卖要求边际成本最低的企业赢得拍卖,拍卖总支付是式(31);如果企业需要先支付固定费项,后支付提成,提成系数与固定费分别是式(24)、式(32);发明人的期望拍卖收益是式(33),并且无需设定保留价格. 4两种拍卖方式的比较 第2节作为基准分析了实践上采用的固定费拍卖,第3节又提出了两部制拍卖.虽然两者在很多方面存在不同,但是本文更关注拍卖的期望收益,以及拍卖成交率的差异. 4.1期望收益与成交率 首先比较拍卖成交率.目前我国技术拍卖成交率并不高,成交困难的情况普遍存在.近年的技术拍卖会,项目必须通过层层筛选,少数精品才能够得到拍卖机会.即便如此,每一届的拍卖成交率也都在40%以下.其他比较普通的技术项目,通过拍卖实现产业化的难度会更大.这就要求比较一下在技术拍卖交易困难的时候,使用固定费拍卖与两部制拍卖的成交率. Prob[c1≤c*A] (37) 技术拍卖中保留成本的大小,决定了拍卖的成交率.保留成本越低,对企业的效率要求越高,拍卖成功的可能越小.式(37)意味着,当技术拍卖可能出现流拍的时候,两部制拍卖的成功率高于实践上采用的固定费拍卖(英式拍卖).当前,选择适当的拍卖方式,提高技术拍卖的成功率,具有积极意义.本文提出的两部制拍卖,因为保留成本更高,所以能够有效提高拍卖成功率. 然后比较拍卖的期望收益.对于固定费拍卖,由式(1),英式拍卖的成交价格是R(c2),发明人的拍卖收益决定于边际成本的次小值c2,或者是保留价格R(c*A).如果采用两部制拍卖,因为成本为c1的企业赢得拍卖,把式(26)中的成本c换为c1,并由式(33),虚拟价值决定于边际成本最小值c1,拍卖期望收益也决定于c1.这意味着两种拍卖期望收益的决定因素不同,大小也可能有区别.因为c*A [1-G(c)]n-1g(c)dc>0 这说明TB>TA.基于以上分析,提出 命题3两部制拍卖的期望收益优于固定费拍卖,同时具有更高的拍卖成功率. 命题3是关键结论,说明本文提出的两部制定价的最优拍卖,全面优于目前实践上使用的固定费(英式)拍卖.把技术当做一般商品,采用英式拍卖的做法,是在套用以往的习惯,对技术拍卖而言并不是最好的.实践上技术拍卖的方式,存在改进的余地. 4.2算例 以下举一个技术两部制拍卖与固定费(英式)拍卖的数值例子,给出均衡结果,并比较两种拍卖方式期望收益与成交率的差异.设企业的边际成本在区间[0,1]上均匀分布,逆需求函数是p=1-q,于是边际成本的分布函数是G(c)=c,分布密度是g(c)=1.另外假定有3家企业参与竞标. 若采用两部制拍卖,由式(35),保留成本满足方程1-c0B-c0B=0,方程的解是c0B=0.5<1,所以取c*B=0.5;由式(36),成交率是 [1-(1-0.5)3]×100%=87.5% 由式(24)、式(32),提成系数与固定费分别是 (38) 于是成本是c的企业赢得拍卖后,将按照式(38)支付固定费与提成.图1给出了固定费F(c)与c的图像关系.F(c)是单调减的,且F(0.5)=0. 图1 F(c)与c的关系 另外,由R(c)=r(c)q(c)+F(c),获胜企业的总支付(固定费+提成)是 (39) 图2给出了R(c)与c的图像关系.R(c)也是单独减的. 图2 R(c)与c的关系 若采用固定费方式拍卖,由式(5),保留成本满足方程1-c0A-2c0A=0,方程的解是c0A=1/3,取c*A=1/3;由式(6),固定费拍卖的成交率是 5结束语 技术拍卖是近年兴起的新的技术交易方式.实践中技术拍卖照搬了一般物品的拍卖形式,常常采用英式拍卖.本文的主要观点是此种拍卖方式并非最优,可以有更好的方式实现技术拍卖. 本文分析了多个企业参加竞拍,但是每个企业边际成本(效率)不同情况下的技术拍卖.首先作为比较的基准,分析了实践上采用的固定费(英式)拍卖,得出了发明人的拍卖期望收益和成交概率;其次,把技术的拍卖价格,与产业化后的产出结合起来,建立了采用“固定费+提成”的两部制定价的技术拍卖模型,得出了最优拍卖机制.最优机制的结果是成本最低的企业赢得拍卖,这是符合社会效率要求的.通过求解最优机制,给出了此机制下获胜企业应该支付技术价格,这包括固定费与提成,以及发明人在拍卖中能够获得的期望收益,与拍卖成交的概率. 通过比较,本文提出的“固定费+提成”的两部制最优拍卖,不仅期望收益高于固定费拍卖,而且具有更高的成交概率,这对于促进技术产业化有积极意义.最后,列举了一个数值例子,作为理论分析的补充.本文的分析,能够对技术拍卖提供新的思路,改善我国目前技术拍卖成交率不高的情况,并能丰富技术定价理论. 参 考 文 献: [1]Sen D, Tauman Y. General licensing schemes for a cost reducing innovation[J]. Games and Economic Behavior, 2007, 59(1): 163-186. [2]Moldovanu B, Sela A. Patent licensing to Bertrand competitors[J]. International Journal of Industrial Organization, 2003, 21(1): 1- 13. [3]Das Varma G. Bidding for aprocess innovation under alternate modes of competition[J]. International Journal of Industrial Organization, 2003, 21(1): 15-37. [4]Goeree J K. Bidding for thefuture: Signaling in auctions with an aftermarket[J]. Journal of Economic Theory, 2003, 108(2): 345-364. [5]谢非, 刘星, 李攀艺. 基于不完全信息动态博弈的技术交易效率研究[J]. 管理工程学报, 2010, 24(2):79-83. Xie Fei, Liu Xing, Li Panyi. A research on the efficiency technology exchange based on an incomplete dynamic game[J]. Journal of Industrial Engineering and Engineering Management, 2010, 24(2): 79-83. (in Chinese) [6]Hoppe H, Jehiel P, Moldovanu B. License auctions and market structure[J]. Journal of Economics & Management Strategy, 2006, 15(2): 371-396. [7]Aniruddha B. Sellinglicenses for a process innovation: The impact of the product market on the selling mechanism[J]. Canadian Journal of Economics, 2008, 41(3): 1015-1045. [8]Janssen M, Karamychev V. Auctions, aftermarket competition, and risk attitudes[J]. International Journal of Industrial Organization, 2009, 27(2): 274-285. [9]Nicolás F, Vasiliki S. The role of optimal threats in auction design[J]. Journal of Economic Theory, 2009, 144(2): 884-897. [10]Hailea P, Hendricksb K, Porter R. Recent U.S. offshore oil and gas lease bidding: A progress report[J]. International Journal of Industrial Organization, 2010, 28(4): 390-396. [11]Caves R. Contractsbetween art and commerce[J]. Journal of Economic Perspectives, 2003, 17(2): 73-83. [12]De Marzo P, Kremer I, Skrzypacz A. Bidding with securities: Auctions and security design[J]. American Economic Review, 2005, 95(4): 936-959. [13]Gorbenko A S, Malenko A. Competition amongsellers in securities auctions[J]. American Economic Review, 2011, 101(5): 1806-1841. [14]Cornelli F, Felli F. How tosell a (bankrupt) company[J]. International Review of Finance, 2012, 12(2): 197-226. [15]Abhishek V, Hajek B, Williams S. Auctions with a prot sharing contract[J]. Games and Economic Behavior, 2013, 77(1): 247-270. [16]Skrzypacz A. Auctions with contingent payments-an overview[J]. International Journal of Industrial Organization, 2013, 31(5):666-675. [17]Mezzetti C. Mechanism design with interdependent valuations: Surplus extraction[J]. Economic Theory, 2007, 31(3): 473-488. [18]葛如一, 张朋柱. 网络创新外包交易机制比较研究[J]. 管理科学学报, 2010, 13(11): 20-26. Ge Ruyi, Zhang Pengzhu. Comparative study of outsourcing mechanisms in online innovation marketplaces[J]. Journal of Management Sciences in China, 2010, 13(11): 20-26. (in Chinese) [19]Che Y. Design competition through multidimensional auctions[J]. RAND Journal of Economics, 1993, 24(4): 668-680. [20]Cachon P, Zhang F. Procuring fast delivery: Sole sourcing with information asymmetry[J]. Management Science, 2006, 52(6): 881-896. [21]王宏, 陈宏民, 杨剑侠. 多维信息招投标中的最优机制及其实施[J]. 管理科学学报, 2010, 13(8):1-14. Wang Hong, Chen Hongmin, Yang Jianxia. Optimal mechanism and its implementation in multidimensional auctions[J]. Journal of Management Sciences in China, 2010, 13(8): 1-14. (in Chinese) [22]Sen D. On the coexistence of different licensing schemes[J]. International Review of Economics and Finance, 2005, 14(14): 393-413. [23]岳贤平, 李廉水, 顾海英. 逆向选择条件下技术许可中排他性价格契约研究[J]. 科学学研究, 2009, 27(1):118-126. Yue Xianping, Li Lianshui, Gu Haiying. Study on exclusive price contracts of technology licensing under the conditions of adverse selection[J]. Studies in Science of Science, 2009, 27(1): 118-126. (in Chinese) [24]石岩, 刘思峰. 不对称信息下需求创新专利授权的最优机制[J]. 预测, 2009, 28(3): 39-44. Shi Yan, Liu Sifeng. Optimal mechanism of demand innovation licensing strategy under asymmetric information[J]. Forecasting, 2009, 28(3): 39-44. (in Chinese) [25]王明喜, 刘树林. 三类风险投标者共存下的一级价格拍卖[J]. 管理科学学报, 2010, 13(8):15-21, 32. Wang Mingxi, Liu Shulin. First-price auction with three types of risk bidders[J]. Journal of Management Sciences in China, 2010, 13(8): 15-21, 32. (in Chinese) 附录1 由式(2) (A1) 对上式中的双重积分做分部积分,有 把-h(c)看作1-H(c)的导数,对上式继续做分部积分,得出 代入式(A1) 因为1-H(c)=[1-G(c)]n-1,另外上式是发明人从1家企业获得的期望拍卖收益,乘以n,得到原文的式(4). 附录2 对于成本为y的企业若宣称成本是z,产量为正值要求a-y>r(z),同时由式(15)得到的信息租金是 (A2) 由此得到 (A3) 假设u(c,x)>u(c,c),此不等式改写成定积分的形式是 再把括号内的项改写成定积分,即可得到 (A4) 如果x>c,对于z∈[c,x],z≥c,所以 因此式(A4)必然不成立,因为二重积分为负.如果x 附录3 把式(15)中的c看作定值,把x看作变量,对后者求微分,一阶条件是 (A5) 另外,把式(14)中的c看作变量,对其求微分是 (A6) 将式(A5)代入式(A6)得到式(17). Optimal mechanism of technology auction SHIYan1,2,XIEFu-ji2,LIULang3 1. School of Economics and Management, Nanchang Hangkong University, Nanchang 330063, China;2. School of Antai Economics and Management, Shanghai Jiaotong University, Shanghai 200052, China;3. School of Economics and Management, East China Jiaotong University, Nanchang 330013, China Abstract:Technology auction in practice often adopts the mode of fixed fee (English) auction, where its price is irrelevant to output. In order to connect technology price with its output, the paper puts forward a two traffic auction mechanism.That is, the winner’s payment consists of a fixed fee and a royalty. At first, English auction is analyzed as a benchmark. Then,an optimal technology auction mechanism of symmetric independent private valueis studied, in which each firm reports its cost. It is found that the winner is the buyer with the lowest cost, fixed fee and royalty of technology price are determined by the firms’ reported cost, and a reserve price is not needed. Two-traffic auctions lead to higher expected revenues for the seller, and a higher auction rate. Key words:technology auction; optimal mechanism; English auction; two-traffic 收稿日期:①2013-08-07; 修订日期:2015-02-22. 基金项目:国家社会科学基金重点资助项目(13AZD015); 国家自然科学基金资助项目(71162024; 71373158); 中国博士后基金资助项目(2013M531181); 上海市博士后基金资助项目(13R21414800); 江西省教育厅科技资助项目(GJJ11504). 作者简介:石岩(1972—), 男, 山东济宁人, 博士, 副教授. Email:shiyuheng001@aliyun.com 中图分类号:F224 文献标识码:A 文章编号:1007-9807(2016)05-0028-13